Chapter 9: Gases

Chapter 9 Practice

9.1 Gas Pressure [Go to section 9.1]

  1. Why are sharp knives more effective than dull knives? (Hint: Think about the definition of pressure.)
  2. Why do some small bridges have weight limits that depend on how many wheels or axles the crossing vehicle has?
  3. Why should you roll or belly crawl rather than walk across a thinly frozen pond?
  4. A typical barometric pressure in Redding, California, is about 750 mm Hg. Calculate this pressure in atm and kPa.
  5. Canadian tire pressure gauges are marked in units of kilopascals. What reading on such a gauge corresponds to 32 psi?
  6. A typical barometric pressure in Kansas City is 740 torr. What is this pressure in atmospheres, in millimeters of mercury, and in kilopascals?
  7. The pressure of the atmosphere on the surface of the planet Venus is about 88.8 atm. Compare that pressure in psi to the normal pressure on earth at sea level in psi.
  8. During the Viking landings on Mars, the atmospheric pressure was determined to be on the average about 6.50 millibars (1 bar = 0.987 atm). What is that pressure in torr and kPa?
  9. Consider this scenario and answer the following questions: On a mid-August day in the northeastern United States, the following information appeared in the local newspaper: atmospheric pressure at sea level 29.97 in., 1013.9 mbar.
    1. What was the pressure in kPa?
    2. The pressure near the seacoast in the northeastern United States is usually reported near 30.0 in. Hg. During a hurricane, the pressure may fall to near 28.0 in. Hg. Calculate the drop in pressure in torr.
  10. A medical laboratory catalog describes the pressure in a cylinder of a gas as 14.82 MPa. What is the pressure of this gas in atmospheres and torr?
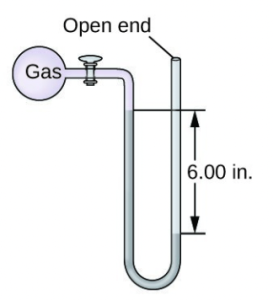
  11. The pressure of a sample of gas is measured at sea level with an open-end mercury manometer. Assuming atmospheric pressure is 760.0 mm Hg, determine the pressure of the gas in:
    1. mm Hg
    2. atm
    3. kPa
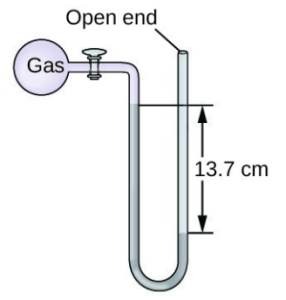
  12. The pressure of a sample of gas is measured with an open-end manometer, partially shown to the right. The liquid in the manometer is mercury. Assuming atmospheric pressure is 29.92 in. Hg, determine the pressure of the gas in:
    1. torr
    2. Pa
    3. bar
Show Selected Solutions
  1. The cutting edge of a knife that has been sharpened has a smaller surface area than a dull knife. Since pressure is force per unit area, a sharp knife will exert a higher pressure with the same amount of force and cut through material more effectively.
  2. Lying down distributes your weight over a larger surface area, exerting less pressure on the ice compared to standing up. If you exert less pressure, you are less likely to break through thin ice.
  3. 2.2 × 102 kPa
  4. 1.3 × 103 psi
  5. The answers are as follows:
    1. 51 torr drop
    2. 711 torr
  6. The answers are as follows:
    1. 623 mm Hg
    2. 0.820 atm
    3. 83.1 kPa


9.2 Relating Pressure, Volume, Amount, and Temperature: The Ideal Gas Law [Go to section 9.2]

  1. Explain how the volume of the bubbles exhausted by a scuba diver (Figure 8.16) change as they rise to the surface, assuming that they remain intact.
  2. Sometimes leaving a bicycle in the sun on a hot day will cause a blowout. Why?
  3. An alternate way to state Avogadro’s law is “All other things being equal, the number of molecules in a gas is directly proportional to the volume of the gas.”
    1. What is the meaning of the term “directly proportional?”
    2. What are the “other things” that must be equal?
  4. One way to state Boyle’s law is “All other things being equal, the pressure of a gas is inversely proportional to its volume.”
    1. What is the meaning of the term “inversely proportional?”
    2. What are the “other things” that must be equal?
  5. How would the graph in Figure 9.2.5 change if the number of moles of gas in the sample used to determine the curve were doubled?
  6. How would the graph in Figure 9.2.4 change if the number of moles of gas in the sample used to determine the curve were doubled?
  7. Determine the volume of 1 mol of [latex]\ce{CH4}[/latex] gas at 150 K and 1 atm, using Figure 9.2.4.
  8. In addition to the data found in Figure 9.2.5, what other information do we need to find the mass of the sample of air used to determine the graph?
  9. How many moles of gaseous boron trifluoride, [latex]\ce{BF3}[/latex], are contained in a 4.3410-L bulb at 788.0 K if the pressure is 1.220 atm? How many grams of [latex]\ce{BF}[/latex]?
  10. Determine the pressure of the gas in the syringe shown in Figure 9.2.5 when its volume is 12.5 mL, using:
    1. the appropriate graph
    2. Boyle’s Law
  11. How many grams of gas are present in each of the following cases?
    1. 0.100 L of [latex]\ce{CO2}[/latex] at 307 torr and 26 °C
    2. 8.75 L of [latex]\ce{C2H4}[/latex], at 378.3 kPa and 483 K
    3. 221 mL of [latex]\ce{Ar}[/latex] at 0.23 torr and –54 °C
  12. What is the temperature of an 11.2-L sample of carbon monoxide, [latex]\ce{CO}[/latex], at 744 torr if it occupies 13.3 L at 55 °C and 744 torr?
  13. A cylinder of medical oxygen has a volume of 35.4 L, and contains [latex]\ce{O2}[/latex] at a pressure of 151 atm and a temperature of 25 °C. What pressure of [latex]\ce{O2}[/latex] does this correspond to at normal body conditions, that is, 1 atm and 37 °C?
  14. A balloon inflated with three breaths of air has a volume of 1.7 L. At the same temperature and pressure, what is the volume of the balloon if five more same-sized breaths are added to the balloon?
  15. A 20.0-L cylinder containing 11.34 kg of butane, [latex]\ce{C4H_{10}}[/latex], was opened to the atmosphere. Calculate the mass of the gas remaining in the cylinder if it were opened and the gas escaped until the pressure in the cylinder was equal to the atmospheric pressure, 0.983 atm, and a temperature of 27 °C.
  16. The volume of an automobile air bag was 66.8 L when inflated at 25 °C with 77.8 g of nitrogen gas. What was the pressure in the bag in kPa?
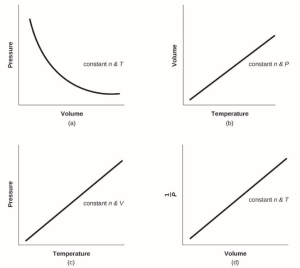
  17. For a given amount of gas showing ideal behavior, draw labeled graphs of:
    1. the variation P with V
    2. the variation of V with T
    3. the variation of P with T
    4. the variation of [latex]\frac{1}{P}[/latex] with V
  18. Iodine, [latex]\ce{I2}[/latex], is a solid at room temperature but sublimes (converts from a solid into a gas) when warmed. What is the temperature in a 73.3-mL bulb that contains 0.292 g of [latex]\ce{I2}[/latex] vapor at a pressure of 0.462 atm?
  19. The effect of chlorofluorocarbons (such as [latex]\ce{CCl2F2}[/latex]) on the depletion of the ozone layer is well known. The use of substitutes, such as [latex]\ce{CH3CH2F}(g)[/latex], for the chlorofluorocarbons, has largely corrected the problem. Calculate the volume occupied by 10.0 g of each of these compounds at STP:
    1. [latex]\ce{CCl2F2}(g)[/latex]
    2. [latex]\ce{CH3CH2F}(g)[/latex]
  20. A high altitude balloon is filled with 1.41 × 104 L of hydrogen at a temperature of 21 °C and a pressure of 745 torr. What is the volume of the balloon at a height of 20 km, where the temperature is –48 °C and the pressure is 63.1 torr?
  21. A balloon with a volume of 100.21 L at 21 °C and 0.981 atm is released and just barely clears the top of Mount Crumpet in British Columbia. If the final volume of the balloon is 144.53 L at a temperature of 5.24 °C, what is the pressure experienced by the balloon as it clears Mount Crumpet?
  22. A large scuba tank with a volume of 18 L is rated for a pressure of 220 bar. The tank is filled at 20 °C and contains enough air to supply 1860 L of air to a diver at a pressure of 2.37 atm (a depth of 45 feet). Was the tank filled to capacity at 20 °C?
  23. If the volume of a fixed amount of a gas is tripled at constant temperature, what happens to the pressure?
  24. While resting, the average 70-kg human man consumes 14 L of pure [latex]\ce{O2}[/latex] per hour at 25 °C and 100 kPa. How many moles of [latex]\ce{O2}[/latex] are consumed by a 70kg man while resting for 1.0 h?
  25. What happens to the pressure of an ideal gas when its volume is doubled at constant temperature?
  26. A liter of methane gas, [latex]\ce{CH4}[/latex], at STP contains more atoms of hydrogen than does a liter of pure hydrogen gas, [latex]\ce{H2}[/latex], at STP. Using Avogadro’s law as a starting point, explain why.
Show Selected Solutions
  1. As the bubbles rise, the pressure decreases, so their volume increases as suggested by Boyle’s law.
  2. The answers are as follows:
    1. The number of particles in the gas increases as the volume increases. This relationship may be written as n = constant × V. It is a direct relationship.
    2. The temperature and pressure must be kept constant.
  3. The curve would be farther to the right and higher up, but the same basic shape.
  4. The figure shows the change in volume for 1 mol of [latex]\ce{CH4}[/latex] gas as a function of temperature. The graph shows that the volume is about 12.5 L.
  5. 5.553 g
  6. The answers are as follows:
    1. 7.24 x 10-2 g;
    2. 23.1 g;
    3. 1.5 x 10-4 g
  7. 173.5 atm
  8. 46.4 g
  10. The answers are as follows:
    1. 1.85 L
    2. 4.66 L
  11. 0.644 atm
  12. The pressure decreases by a factor of 3.
  13. The pressure decreases by half.


9.3 Applications of the Ideal Gas Law [Go to section 9.3]

  1. A cylinder of [latex]\ce{O2}(g)[/latex] used in breathing by patients with emphysema has a volume of 3.00 L at a pressure of 10.0 atm. If the temperature of the cylinder is 28.0 °C, what mass of oxygen is in the cylinder?
  2. What is the density of laughing gas, dinitrogen monoxide, [latex]\ce{N2O}[/latex], at a temperature of 325 K and a pressure of 113.0 kPa?
  3. The density of a certain gaseous fluoride of phosphorus is 3.93 g/L at STP. Calculate the molar mass of this fluoride and determine its molecular formula.
  4. Which is denser at the same temperature and pressure, dry air or air saturated with water vapor? Explain.
  5. Predict the molar mass and identity of 0.23 g of a gas that occupies 0.20 L at 298 K.
Show Selected Solutions
  1. 38.8 g
  2. 88.1 g mol-1; [latex]\ce{PF3}[/latex]
  3. M=28 g/mol, [latex]\ce{N2}[/latex]


9.4 Mixtures of Gases and Partial Pressures [Go to section 9.4]

  1. One molecule of hemoglobin will combine with four molecules of oxygen. If 1.0 g of hemoglobin combines with 1.53 mL of oxygen at body temperature (37 °C) and a pressure of 743 torr, what is the molar mass of hemoglobin?
  2. A 36.0–L cylinder of a gas used for calibration of blood gas analyzers in medical laboratories contains 350 g [latex]\ce{CO2}[/latex], 805 g [latex]\ce{O2}[/latex], and 4,880 g [latex]\ce{N2}[/latex]. At 25° C, what is the pressure in the cylinder in atmospheres, in torr, and in kilopascals?
  3. One method of analyzing amino acids is the van Slyke method. The characteristic amino groups ([latex]\ce{-NH2}[/latex]) in protein material are allowed to react with nitrous acid, [latex]\ce{HNO2}[/latex], to form [latex]\ce{N2}[/latex] gas. From the volume of the gas, the amount of amino acid can be determined. A 0.0604g sample of a biological sample containing glycine, [latex]\ce{CH2(NH2)COOH}[/latex], was analyzed by the van Slyke method and yielded 3.70 mL of N2 collected over water at a pressure of 735 torr and 29 °C. What was the percentage of glycine in the sample?  [latex]\ce{CH2(NH2)CO2H} + \ce{HNO2} \longrightarrow \ce{CH2(OH)CO2H} + \ce{H2O} + \ce{N2}[/latex]
  4. Most mixtures of hydrogen gas with oxygen gas are explosive. However, a mixture that contains less than 3.0 % [latex]\ce{O2}[/latex] is not. If enough [latex]\ce{O2}[/latex] is added to a cylinder of [latex]\ce{H2}[/latex] at 33.2 atm to bring the total pressure to 34.5 atm, is the mixture explosive?
  5. Consider this question: What is the molecular formula of a compound that contains 39% [latex]\ce{C}[/latex], 45% [latex]\ce{N}[/latex], and 16% [latex]\ce{H}[/latex] if 0.157 g of the compound occupies 125 mL with a pressure of 99.5 kPa at 22 °C?
  6. A sample of a compound of xenon and fluorine was confined in a bulb with a pressure of 18 torr. Hydrogen was added to the bulb until the pressure was 72 torr. Passage of an electric spark through the mixture produced [latex]\ce{Xe} \text{ and } \ce{HF}[/latex]. After the [latex]\ce{HF}[/latex] was removed by reaction with solid [latex]\ce{KOH}[/latex], the final pressure of xenon and unreacted hydrogen in the bulb was 36 torr. What is the empirical formula of the xenon fluoride in the original sample? (Note: Xenon fluorides contain only one xenon atom per molecule.)
  7. A cylinder of a gas mixture used for calibration of blood gas analyzers in medical laboratories contains 5.0% [latex]\ce{CO2}[/latex], 12.0% [latex]\ce{O2}[/latex], and the remainder [latex]\ce{N2}[/latex] at a total pressure of 146 atm. What is the partial pressure of each component of this gas? (The percentages given indicate the percent of the total pressure that is due to each component.)
  8. What is the volume of a mixture of 1.25 g each of [latex]\ce{CO2, O2}, \text{ and } \ce{Ar}[/latex] at STP? Assume ideal gas behavior.
Show Selected Solutions
  1. 141 atm, 107,000 torr, 14,300 kPa
  2. Yes, the mixture is explosive.
  3. [latex]\ce{XeF4}[/latex]
  4. 2.21 L


9.5 Stoichiometry of Reactions Involving Gases [Go to section 9.5]

  1. Automobile air bags are inflated with nitrogen gas, which is formed by the decomposition of solid sodium azide ([latex]\ce{NaN3}[/latex]). The other product is sodium metal. Calculate the volume of nitrogen gas at 27 °C and 756 torr formed by the decomposition of 125 g of sodium azide.
  2. What volume of oxygen at 423.0 K and a pressure of 127.4 kPa is produced by the decomposition of 129.7 g of [latex]\ce{BaO2}[/latex] to [latex]\ce{BaO}[/latex] and [latex]\ce{O2}[/latex]?
  3. Before small batteries were available, carbide lamps were used for bicycle lights. Acetylene gas, [latex]\ce{C2H2}[/latex], and solid calcium hydroxide were formed by the reaction of calcium carbide, [latex]\ce{CaC2}[/latex], with water. The ignition of the acetylene gas provided the light. Currently, the same lamps are used by some cavers, and calcium carbide is used to produce acetylene for carbide cannons.
    1. Outline the steps necessary to answer the following question: What volume of [latex]\ce{C2H2}[/latex] at 1.005 atm and 12.2 °C is formed by the reaction of 15.48 g of [latex]\ce{CaC2}[/latex] with water?
    2. Answer the question.
  4. The chlorofluorocarbon [latex]\ce{CCl2F2}[/latex] can be recycled into a different compound by reaction with hydrogen to produce [latex]\ce{CH2F2}(g)[/latex], a compound useful in chemical manufacturing:  [latex]\ce{CCl2F2}(g) + 4\ce{H2}(g) \longrightarrow \ce{CH2F2}(g) + 2\ce{HCl}(g)[/latex]
    1. Outline the steps necessary to answer the following question: What volume of hydrogen at 225 atm and 35.5 °C would be required to react with 1 ton (1.000 × 103 kg) of [latex]\ce{CCl2F2}[/latex]?
    2. Answer the question.
  5. What volume of [latex]\ce{O2}[/latex] at STP is required to oxidize 8.0 L of [latex]\ce{NO}[/latex] at STP to [latex]\ce{NO2}[/latex]? What volume of [latex]\ce{NO2}[/latex] is produced at STP?
  6. Lime, [latex]\ce{CaO}[/latex], is produced by heating calcium carbonate, [latex]\ce{CaCO3}[/latex]; carbon dioxide is the other product.
    1. Outline the steps necessary to answer the following question: What volume of carbon dioxide at 875 K and 0.966 atm is produced by the decomposition of 1 ton (1.000 × 103 kg) of calcium carbonate?
    2. Answer the question.
  7. Methanol, [latex]\ce{CH3OH}[/latex], is produced industrially by the following reaction:  [latex]\ce{CO}(g) + 2\ce{H2}(g)\text{       }\underrightarrow{\text{copper catalyst 300 °C, 300 atm}}\text{       } \ce{CH3OH}(g)[/latex]
    Assuming that the gases behave as ideal gases, find the ratio of the total volume of the reactants to the final volume.
  8. Calculate the volume of oxygen required to burn 12.00 L of ethane gas, [latex]\ce{C2H6}[/latex], to produce carbon dioxide and water, if the volumes of [latex]\ce{C2H6}[/latex] and [latex]\ce{O2}[/latex] are measured under the same conditions of temperature and pressure.
  9. Ethanol, [latex]\ce{C2H3OH}[/latex], is produced industrially from ethylene, [latex]\ce{C2H4}[/latex], by the following sequence of reactions:
    [latex]\begin{array}{l} \ce{3C2H4} + 2\ce{H2SO4} \longrightarrow \ce{C2H3HSO4} + \ce{(C2H5)2SO4} \\ \ce{C2H5HSO4} + \ce{(C2H5)2SO4} + \ce{3H2O} \longrightarrow \ce{3C2H5OH} + \ce{2H2SO4}\\ \end{array}[/latex]
    What volume of ethylene at STP is required to produce 1.000 metric ton (1000 kg) of ethanol if the overall yield of ethanol is 90.1%?
  10. Consider the following questions:
    1. What is the total volume of the [latex]\ce{CO2}(g)[/latex] and [latex]\ce{H2O}(g)[/latex] at 600 °C and 0.888 atm produced by the combustion of 1.00 L of [latex]\ce{C2H6}[/latex](g) measured at STP?
    2. What is the partial pressure of [latex]\ce{H2O}[/latex] in the product gases?
Show Selected Solutions
  1. 10.57 L
  2. The answers are as follows:
    1. Determine the molar mass of [latex]\ce{CCl2F2}[/latex]. From the balanced equation, calculate the moles of [latex]\ce{H2}[/latex] needed for the complete reaction. From the ideal gas law, convert moles of [latex]\ce{H2}[/latex]into volume.
    2. 3.72 × 103 L
  3. The answers are as follows:
    1. Balance the equation. Determine the grams of [latex]\ce{CO2}[/latex] produced and the number of moles. From the ideal gas law, determine the volume of gas.
    2. 7.43 × 105 L
  4. 42.00 L
  5. The answers are as follows:
    1. 18.0 L
    2. 0.533 atm


9.6 Effusion and Diffusion of Gases [Go to section 9.6]

  1. Explain why the numbers of molecules are not identical in the left- and right-hand bulbs shown in the center illustration of Figure 9.6.1.
  2. A balloon filled with helium gas takes 6 hours to deflate to 50% of its original volume. How long will it take for an identical balloon filled with the same volume of hydrogen gas (instead of helium) to decrease its volume by 50%?
  3. During the discussion of gaseous diffusion for enriching uranium, it was claimed that [latex]\ce{^{235}UF6}[/latex] diffuses 0.4% faster than [latex]\ce{^{238}UF6}[/latex] Show the calculation that supports this value. The molar mass of [latex]\ce{^{235}UF6}[/latex] = 235.043930 + 6 × 18.998403 = 349.034348 g/mol, and the molar mass of [latex]\ce{^{238}UF6}[/latex] = 238.050788 + 6 × 18.998403 = 352.041206 g/mol.
  4. Starting with the definition of rate of effusion and Graham’s finding relating rate and molar mass, show how to derive the Graham’s law equation, relating the relative rates of effusion for two gases to their molecular masses.
  5. When two cotton plugs, one moistened with ammonia and the other with hydrochloric acid, are simultaneously inserted into opposite ends of a glass tube that is 87.0 cm long, a white ring of [latex]\ce{NH4Cl}[/latex] forms where gaseous [latex]\ce{NH3}[/latex] and gaseous [latex]\ce{HCl}[/latex] first come into contact. (Hint: Calculate the rates of diffusion for both [latex]\ce{NH3}[/latex] and [latex]\ce{HCl}[/latex], and find out how much faster [latex]\ce{NH3}[/latex] diffuses than [latex]\ce{HCl}[/latex].) [latex]\ce{NH3}(g) + \ce{HCl}(g) \longrightarrow \ce{NH4Cl}(s)[/latex]  At approximately what distance from the ammonia-moistened plug does this occur?
  6. Calculate the relative rate of diffusion of [latex]\ce{^1H2}[/latex] (molar mass 2.0 g/mol) compared with [latex]\ce{^2H2}[/latex] (molar mass 4.0 g/mol) and the relative rate of diffusion of [latex]\ce{O2}[/latex] (molar mass 32 g/mol) compared to that of [latex]\ce{O3}[/latex] (molar mass 48 g/mol).
Show Selected Solutions
  1. 4.2 hours
  2. [latex]\frac{v_A}{v_B} = ( \frac{m_B}{m_A})^{\frac{1}{2}}[/latex]
  3. [latex]\frac{R_{\ce{H2}}}{R_{\ce{D2}}} = 1.4 \frac{R_{\ce{O2}}}{R_{\ce{O3}}} = 1.2[/latex]


9.7 The Kinetic-Molecular Theory [Go to section 9.7]

  1. Using the postulates of the kinetic-molecular theory, explain why a gas uniformly fills a container of any shape.
  2. Can the speed of a given molecule in a gas double at constant temperature? Explain your answer.
  3. Describe what happens to the average kinetic energy of ideal gas molecules when the conditions are changed as follows:
    1. The pressure of the gas is increased by reducing the volume at constant temperature.
    2. The pressure of the gas is increased by increasing the temperature at constant volume.
    3. The average speed of the molecules is increased by a factor of 2.
  4. A 1L sample of [latex]\ce{CO}[/latex] initially at STP is heated to 546 K, and its volume is increased to 2 L.
    1. What effect do these changes have on the number of collisions of the molecules of the gas per unit area of the container wall?
    2. What is the effect on the average kinetic energy of the molecules?
    3. What is the effect on the root mean square speed of the molecules?
Show Selected Solutions
  1. Yes. At any given instant, there are a range of values of molecular speeds in a sample of gas. Any single molecule can speed up or slow down as it collides with other molecules. The average speed of all the molecules is constant at constant temperature.
  2. Both the temperature and the volume are doubled for this gas (n constant), so P remains constant.
    1. The number of collisions per unit area of the container wall is constant.
    2. The average kinetic energy doubles; it is proportional to temperature.
    3. The root mean square speed increases to [latex]\sqrt{2}[/latex] times its initial value; urms is proportional to [latex]\sqrt{KE_{avg}}[/latex].


9.8 Non-Ideal Gas Behavior [Go to section 9.8]

  1. Describe the factors responsible for the deviation of the behavior of real gases from that of an ideal gas.
  2. For which of the following gases should the correction for the molecular volume be largest:  [latex]\ce{CO, CO2, H2, He, NH3, SF6}[/latex]?
  3. Answer the following questions:
    1. If XX behaved as an ideal gas, what would its graph of Z vs. P look like?
    2. For most of this chapter, we performed calculations treating gases as ideal. Was this justified?
    3. What is the effect of the volume of gas molecules on Z? Under what conditions is this effect small? When is it large? Explain using an appropriate diagram.
    4. What is the effect of intermolecular attractions on the value of Z? Under what conditions is this effect small? When is it large? Explain using an appropriate diagram.
    5. In general, under what temperature conditions would you expect Z to have the largest deviations from the Z for an ideal gas?
Show Selected Solutions
  1. We would expect the molecule with the largest volume to need the largest correction. [latex]\ce{SF6}[/latex] would need the largest correction.


License

Icon for the Creative Commons Attribution-NonCommercial-ShareAlike 4.0 International License

Chemistry Fundamentals Copyright © by Dr. Julie Donnelly, Dr. Nicole Lapeyrouse, and Dr. Matthew Rex is licensed under a Creative Commons Attribution-NonCommercial-ShareAlike 4.0 International License, except where otherwise noted.

Share This Book