Chapter 9: Gases
9.5 Stoichiometry of Reactions Involving Gases
Learning Outcomes
- Use balanced chemical equations to relate the volumes of gas-phase reactants and products using the stoichiometry of the reaction and the ideal gas law
Chemical Stoichiometry and Gases
Chemical stoichiometry describes the quantitative relationships between reactants and products in chemical reactions.
We have previously measured quantities of reactants and products using masses for solids and volumes in conjunction with the molarity for solutions; now we can also use gas volumes to indicate quantities. If we know the volume, pressure, and temperature of a gas, we can use the ideal gas equation to calculate how many moles of the gas are present. If we know how many moles of a gas are involved, we can calculate the volume of a gas at any temperature and pressure.
Avogadro’s Law Revisited
Sometimes we can take advantage of a simplifying feature of the stoichiometry of gases that solids and solutions do not exhibit: All gases that show ideal behavior contain the same number of molecules in the same volume (at the same temperature and pressure). Thus, the ratios of volumes of gases involved in a chemical reaction are given by the coefficients in the equation for the reaction, provided that the gas volumes are measured at the same temperature and pressure.
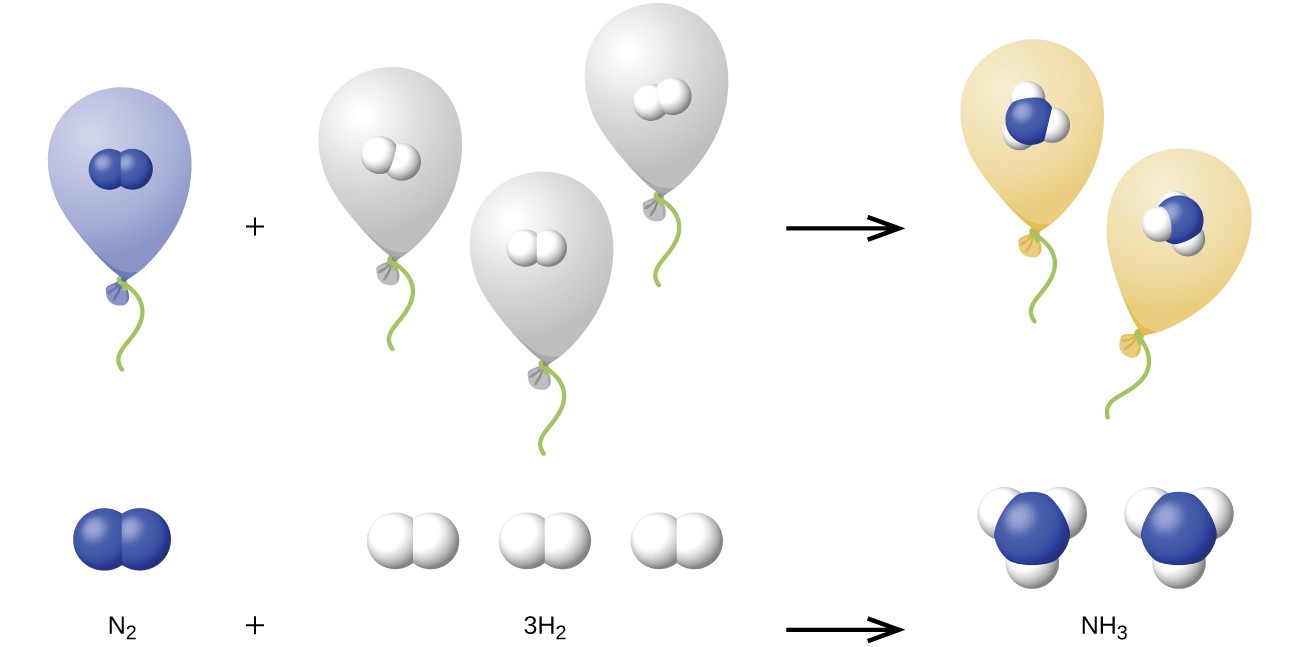
We can extend Avogadro’s law (that the volume of a gas is directly proportional to the number of moles of the gas) to chemical reactions with gases: Gases combine, or react, in definite and simple proportions by volume, provided that all gas volumes are measured at the same temperature and pressure. For example, since nitrogen and hydrogen gases react to produce ammonia gas according to [latex]{\ce{N}}_{2}\left(g\right)+3{\ce{H}}_{2}\left(g\right)\rightarrow{2{\ce{NH}}}_{3}\left(g\right)[/latex], a given volume of nitrogen gas reacts with three times that volume of hydrogen gas to produce two times that volume of ammonia gas, if pressure and temperature remain constant.
The explanation for this is illustrated in Figure 9.5.1. According to Avogadro’s law, equal volumes of gaseous [latex]\ce{N2}[/latex], [latex]\ce{H2}[/latex], and [latex]\ce{NH3}[/latex], at the same temperature and pressure, contain the same number of molecules. Because one molecule of [latex]\ce{N2}[/latex] reacts with three molecules of [latex]\ce{H2}[/latex] to produce two molecules of [latex]\ce{NH3}[/latex], the volume of [latex]\ce{H2}[/latex] required is three times the volume of [latex]\ce{N2}[/latex], and the volume of [latex]\ce{NH3}[/latex] produced is two times the volume of [latex]\ce{N2}[/latex].
Example 9.5.1: Reaction of Gases
Propane, [latex]\ce{C3H8}[/latex](g), is used in gas grills to provide the heat for cooking. What volume of [latex]\ce{O2}[/latex](g) measured at 25 °C and 760 torr is required to react with 2.7 L of propane measured under the same conditions of temperature and pressure? Assume that the propane undergoes complete combustion.
Show Solution
The ratio of the volumes of [latex]\ce{C3H8}[/latex] and [latex]\ce{O2}[/latex] will be equal to the ratio of their coefficients in the balanced equation for the reaction:
[latex]\begin{array}{ccccccc}{\ce{C}}_{3}{\ce{H}}_{8}\left(g\right)&+&5{\ce{O}}_{2}\left(g\right)&\longrightarrow&3{\ce{CO}}_{2}\left(g\right)&+&4{\ce{H}}_{2}\ce{O}\left(l\right)\\ \text{1 volume}&+&\text{5 volumes}&{}&\text{3 volumes}&+&\text{4 volumes}\end{array}[/latex]
From the equation, we see that one volume of [latex]\ce{C2H8}[/latex] will react with five volumes of [latex]\ce{O2}[/latex]:
[latex]2.7\cancel{\text{L}{\ce{C}}_{3}{\ce{H}}_{8}}\times \dfrac{\text{5 L}{\ce{O}}_{2}}{1\cancel{\text{L}{\ce{C}}_{3}{\ce{H}}_{8}}}=\text{13.5 L}{\ce{O}}_{2}[/latex]
A volume of 13.5 L of [latex]\ce{O2}[/latex] will be required to react with 2.7 L of [latex]\ce{C3H8}[/latex].
Check Your Learning
Example 9.5.2: Volumes of Reacting Gases
Ammonia is an important fertilizer and industrial chemical. Suppose that a volume of 683 billion cubic feet of gaseous ammonia, measured at 25 °C and 1 atm, was manufactured. What volume of [latex]\ce{H2}[/latex](g), measured under the same conditions, was required to prepare this amount of ammonia by reaction with [latex]\ce{N2}[/latex]?
[latex]{\ce{N}}_{2}\left(g\right)+3{\ce{H}}_{2}\left(g\right)\rightarrow 2{\ce{NH}}_{3}\left(g\right)[/latex]
Show Solution
Because equal volumes of [latex]\ce{H2}[/latex] and [latex]\ce{NH3}[/latex] contain equal numbers of molecules and each three molecules of [latex]\ce{H2}[/latex] that react produce two molecules of [latex]\ce{NH3}[/latex], the ratio of the volumes of [latex]\ce{H2}[/latex] and [latex]\ce{NH3}[/latex] will be equal to 3:2. Two volumes of [latex]\ce{NH3}[/latex], in this case in units of billion ft3, will be formed from three volumes of [latex]\ce{H2}[/latex]:
[latex]683\cancel{\text{ billion}{\text{ ft }}^{3}{\ce{NH}}_{3}}\times \dfrac{\text{ 3 billion}{\text{ ft }}^{3}{\ce{H}}_{2}}{2\cancel{\text{ billion}{\text{ ft }}^{3}{\ce{NH}}_{3}}}=1.02\times {10}^{3}\text{ billion }{\text{ ft }}^{3}{\ce{H}}_{2}[/latex]
The manufacture of 683 billion ft3 of [latex]\ce{NH3}[/latex] required 1020 billion ft3 of [latex]\ce{H2}[/latex]. (At 25 °C and 1 atm, this is the volume of a cube with an edge length of approximately 1.9 miles.)
Check Your Learning
Example 9.5.3: Volume of Gaseous Product
What volume of hydrogen at 27 °C and 723 torr may be prepared by the reaction of 8.88 g of gallium with an excess of hydrochloric acid?
[latex]2\ce{Ga}\left(s\right)+6\ce{HCl}\left(aq\right)\rightarrow 2{\ce{GaCl}}_{3}\left(aq\right)+3{\ce{H}}_{2}\left(g\right)[/latex]
Show Solution
To convert from the mass of gallium to the volume of [latex]\ce{H2}[/latex](g), we need to do something like this:

The first two conversions are:
[latex]8.88\cancel{\ce{g Ga}}\times \dfrac{1\cancel{\text{mol } \ce{Ga}}}{69.723\cancel{\text{g } \ce{Ga}}}\times \dfrac{\text{3 mol}{\ce{H}}_{2}}{2\cancel{\text{mol } \ce{Ga}}}=0.191{\text{mol } \ce{H}}_{2}[/latex]
Finally, we can use the ideal gas law:
[latex]{V}_{{\ce{H}}_{2}}={\left(\dfrac{nRT}{P}\right)}_{{\text{H}}_{2}}=\dfrac{0.191\cancel{\text{mol}}\times \text{0.08206 L}\cancel{\text{atm}{\text{mol}}^{-\text{1}}{\text{K}}^{-\text{1}}}\times \text{300 K}}{0.951\cancel{\text{atm}}}=\text{4.94 L}[/latex]
Check Your Learning
Key Concepts and Summary
Avogadro’s law may be used in stoichiometric computations for chemical reactions involving gaseous reactants or products.
Try It
- Joseph Priestley first prepared pure oxygen by heating mercuric oxide, [latex]\ce{HgO}[/latex]: [latex]2\ce{HgO}\left(s\right)\rightarrow 2\ce{Hg}\left(l\right)+{\ce{O}}_{2}\left(g\right)[/latex]
- Outline the steps necessary to answer the following question: What volume of [latex]\ce{O2}[/latex] at 23° C and 0.975 atm is produced by the decomposition of 5.36 g of [latex]\ce{HgO}[/latex]?
- Answer the question.
- Cavendish prepared hydrogen in 1766 by the novel method of passing steam through a red-hot gun barrel:[latex]4{\ce{H}}_{2}\ce{O}\left(g\right)+3\ce{Fe}\left(s\right)\rightarrow{\ce{Fe}}_{3}{\ce{O}}_{4}\left(s\right)+4{\ce{H}}_{2}\left(g\right)[/latex]
- Outline the steps necessary to answer the following question: What volume of [latex]\ce{H2}[/latex] at a pressure of 745 torr and a temperature of 20 °C can be prepared from the reaction of 15.O g of [latex]\ce{H2O}[/latex]?
- Answer the question.
Selected Answers
- The answers are as follows:
- Determine the moles of [latex]\ce{HgO}[/latex] that decompose; using the chemical equation, determine the moles of [latex]\ce{O2}[/latex] produced by decomposition of this amount of [latex]\ce{HgO}[/latex]; and determine the volume of [latex]\ce{O2}[/latex] from the moles of [latex]\ce{O2}[/latex], temperature, and pressure.
- [latex]\begin{array}{l}\\ \\ 5.36\cancel{\text{g} \ce{HgO}}\times \frac{\text{1 mol HgO}}{\left(200.59+15.9994\right)\cancel{\text{g } \ce{HgO}}}=\text{0.0247 mol } \ce{HgO}\\ 0.0247\cancel{\text{mol } \ce{HgO}}\times \frac{\text{1 mol}{\ce{O}}_{2}}{2\cancel{\text{mol } \ce{HgO}}}=\text{0.01235 mol}{\ce{O}}_{2}\end{array}[/latex]
PV = nRT
P = 0.975 atm
T = (23.0 + 273.15) K
[latex]V=\frac{nRT}{P}=\frac{0.01235\cancel{\text{mol}}\left(\text{0.08206 L}\cancel{\text{atm}}\cancel{{\text{mol}}^{-\text{1}}}\cancel{{\text{K}}^{-\text{1}}}\right)\left(296.15\cancel{\text{K}}\right)}{0.975\cancel{\text{atm}}}=0.308\text{ L}[/latex]
Glossary
Dalton’s law of partial pressures: total pressure of a mixture of ideal gases is equal to the sum of the partial pressures of the component gases.
mole fraction: concentration unit defined as the ratio of the molar amount of a mixture component to the total number of moles of all mixture components
partial pressure: pressure exerted by an individual gas in a mixture
vapor pressure of water: pressure exerted by water vapor in equilibrium with liquid water in a closed container at a specific temperature

