Chapter 3: The Quantum-Mechanical Model of the Atom

Chapter 3 Practice

3.1 Electromagnetic Energy [Go to section 3.1]

  1. FM–95, an FM radio station, broadcasts at a frequency of 9.51 × 107 s-1 (95.1 MHz). What is the wavelength of these radio waves in meters?
  2. An FM radio station found at 103.1 on the FM dial broadcasts at a frequency of 1.031 ×  108 s-1 (103.1 MHz). What is the wavelength of these radio waves in meters?
  3. When rubidium ions are heated to a high temperature, two lines are observed in its line spectrum at wavelengths (a) 7.9 × 10-7 m and (b) 4.2 × 10-7 m. What are the frequencies of the two lines? What color do we see when we heat a rubidium compound?
Show Selected Solutions
  1. 3.15 m


3.2 Quantum Theory [Go to section 3.2]

  1. A bright violet line occurs at 435.8 nm in the emission spectrum of mercury vapor. What amount of energy, in joules, must be released by an electron in a mercury atom to produce a photon of this light?
  2. The light produced by a red neon sign is due to the emission of light by excited neon atoms. Qualitatively describe the spectrum produced by passing light from a neon lamp through a prism.
  3. Heated lithium atoms emit photons of light with an energy of 2.961 10-19 J. Calculate the frequency and wavelength of one of these photons. What is the total energy in 1 mole of these photons? What is the color of the emitted light?
  4. Light with a wavelength of 614.5 nm looks orange. What is the energy, in joules, per photon of this orange light? What is the energy in eV (1 eV = 1.602 × 10-19 J)?
  5. A photon of light produced by a surgical laser has an energy of 3.027 × 10-19 J. Calculate the frequency and wavelength of the photon. What is the total energy in 1 mole of photons? What is the color of the emitted light?
  6. One of the radiographic devices used in a dentist’s office emits an X-ray of wavelength 2.090 × 10-11 m. What is the energy, in joules, and frequency of this X-ray?
  7. Answer the following questions about a Blu-ray laser:
    1. The laser on a Blu-ray player has a wavelength of 405 nm. In what region of the electromagnetic spectrum is this radiation? What is its frequency?
    2. A Blu-ray laser has a power of 5 milliwatts (1 watt = 1 J s-1). How many photons of light are produced by the laser in 1 hour?
  8. RGB color television and computer displays use cathode ray tubes that produce colors by mixing red, green, and blue light. If we look at the screen with a magnifying glass, we can see individual dots turn on and off as the colors change. Using a spectrum of visible light, determine the approximate wavelength of each of these colors. What is the frequency and energy of a photon of each of these colors?  
  9. Calculate the maximum kinetic energy of an electron ejected by a photon, with a wavelength of 52nm, from a metal with a binding energy of 3.7eV (1eV = 1.602 × 10-19 J).
Show Selected Solutions
  1. The spectrum consists of colored lines, at least one of which (probably the brightest) is red.
  2. 2.018 eV
  3. 9.502 x 10-15 J; 1.434 × 1019  s-1
  4. See Figure 3.13. Red: 660 nm; 4.54 × 1014 Hz; 3.01 × 10-19 J. Green: 520 nm; 5.77 × 1014 Hz; 3.82 × 10-19 J. Blue: 440 nm; 6.81 × 1014 Hz; 4.51 × 10-19 J. Somewhat different numbers are also possible.


3.3 The Bohr Model [Go to section 3.3]

  1. What does it mean to say that the energy of the electrons in an atom is quantized?  
  2. Why is the electron in a Bohr hydrogen atom bound less tightly when it has a quantum number of 3 than when it has a quantum number of 1?
  3. The electron volt (eV) is a convenient unit of energy for expressing atomic-scale energies. It is the amount of energy that an electron gains when subjected to a potential of 1 volt; 1 eV = 1.602 × 10-19 J. Using the Bohr model, determine the energy, in electron volts, of the photon produced when an electron in a hydrogen atom moves from the orbit with n = 5 to the orbit with n = 2. Show your calculations.
  4. Using the Bohr model, determine the energy, in joules, necessary to ionize a ground-state hydrogen atom. Show your calculations.
  5. Using the Bohr model, determine the lowest possible energy for the electron in the [latex]\ce{He^+}[/latex] ion
  6. Using the Bohr model, determine the lowest possible energy, in joules, for the electron in the [latex]\ce{Li^{2+}}[/latex] ion
  7. Using the Bohr model, determine the energy of an electron with n = 8 in a hydrogen atom.
  8. Using the Bohr model, determine the energy of an electron with n = 6 in a hydrogen atom.
  9. What is the radius, in angstroms, of the orbital of an electron with n = 8 in a hydrogen atom?
  10. How far from the nucleus in angstroms (1 angstrom = 1 × 10-10 m) is the electron in a hydrogen atom if it has an energy of –8.72 × 10-20 J?
  11. Using the Bohr model, determine the energy in joules of the photon produced when an electron in a [latex]\ce{Li^{2+}}[/latex] ion moves from the orbit with n = 2 to the orbit with n = 1.
  12. Using the Bohr model, determine the energy in joules of the photon produced when an electron in a [latex]\ce{He^+}[/latex] ion moves from the orbit with n = 5 to the orbit with n = 2.
  13. Calculate the frequencies, wavelengths, and energies associated with the transition of electrons in the n = 3 orbit of a hydrogen atom to the n = 2 and n = 1 orbits.
Show Selected Solutions
  1. Quantized energy means that the electrons can possess only certain discrete energy values; values between those quantized values are not permitted.
  2. 2.856 eV
  3. -8.716 × 10-18 J
  4. -3.405 × 10-20 J
  5. 33.9 Å
  6. 1.471 × 10-17 J
  7. Transition Wavelength (nm) Frequency (s-1) Energy (J)
    n3→ n2 656 4.57 × 1014 -3.03 × 10-19
    n3 → n1 102 2.93 × 1015 -1.94 × 10-18
    n2 → n1 121 2.48 × 1015 -1.64 × 10-18


3.4 The Wavelength Nature of Matter [Go to section 3.4]

  1. Which of the equations from Section 3.4 describe particle-like behavior? Which describe wavelike behavior? Do any involve both types of behavior? Describe the reasons for your choices.
  2. Calculate the minimum uncertainty in the velocity of an electron that has an uncertainty of 600 pm in its position.
Show Selected Solutions
  1. 9.65 × 104 m/s


3.5 Quantum Mechanics and The Atom [Go to section 3.5]

  1. What are the allowed values for each of the four quantum numbers: n, l, ml, and ms?
  2. Describe the properties of an electron associated with each of the following four quantum numbers: n, l, ml, and ms.
  3. Answer the following questions:
    1. Without using quantum numbers, describe the differences between the shells, sub-shells, and orbitals of an atom.
    2. How do the quantum numbers of the shells, sub-shells, and orbitals of an atom differ?
  4. Identify the sub-shell in which electrons with the following quantum numbers are found:
    1. n = 2, l = 1
    2. n = 4, l = 2
    3. n = 6, l = 0
  5. Which of the sub-shells described in Exercise 35 contain degenerate orbitals? How many degenerate orbitals are in each?
  6. Identify the sub-shell in which electrons with the following quantum numbers are found:
    1. n = 3, l = 2
    2. n = 1, l = 0
    3. n = 4, l = 3
  7. Which of the sub-shells described in Exercise 37 contain degenerate orbitals? How many degenerate orbitals are in each?
  8. Write a set of quantum numbers for each of the electrons with an n of 4 in a Se atom.
  9. How many electrons could be held in the second shell of an atom if the spin quantum number ms could have three values instead of just two? (Hint: Consider the Pauli exclusion principle.)
Show Selected Solutions
  1. n determines the general range for the value of energy and the probable distances that the electron can be from the nucleus. l determines the shape of the orbital. m1 determines the orientation of the orbitals of the same l value with respect to one another. ms determines the spin of an electron.
  2. The answers are as follows:
    1. 2p
    2. 4d
    3. 6s
  3. The answers are follows:
    1. 3d
    2. 1s
    3. 4f
  4. n l ml s
    4 0 0 +1/2
    4 0 0 -1/2
    4 1 -1 +1/2
    4 1 0 +1/2
    4 1 +1 +1/2
    4 1 -1 -1/2


3.6 The Shape of Atomic Orbitals [Go to section 3.6]

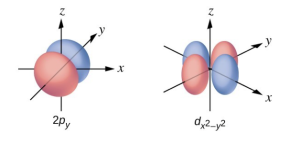
  1. Sketch the boundary surface of a dx2-y2 and a py orbital. Be sure to show and label the axes.
  2. Sketch the px and dxz orbitals. Be sure to show and label the coordinates.
  3. Consider the orbitals shown here in outline.

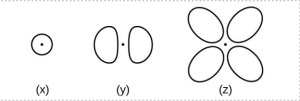
    Three orbital shells x, y, and z that have a quadratic increase in amount of circles that loop the center dot.

    1. What is the maximum number of electrons contained in an orbital of type (x)? Of type (y)? Of type (z)?
    2. How many orbitals of type (x) are found in a shell with n = 2? How many of type (y)? How many of type (z)?
    3. Write a set of quantum numbers for an electron in an orbital of type (x) in a shell with n = 4. Of an orbital of type (y) in a shell with n = 2. Of an orbital of type (z) in a shell with n = 3.
    4. What is the smallest possible n value for an orbital of type (x)? Of type (y)? Of type (z)?
    5. What are the possible l and ml values for an orbital of type (x)? Of type (y)? Of type (z)?
Show Selected Solutions
  2. The answers are as follows:
    1. x. 2, y. 2, z. 2;
    2. x. 1, y. 3, z. 0;
    3. x. 4 0 0 1/2, y. 2 1 0 1/2, z. 3 2 0 1/2;
    4. x. 1, y. 2, z. 3;
    5. x. l = 0, ml = 0, y. l = 1, ml  = –1 0 or +1, z. l = 2, ml = –2 –1 0 +1 +2


License

Icon for the Creative Commons Attribution-NonCommercial-ShareAlike 4.0 International License

Chemistry Fundamentals Copyright © by Dr. Julie Donnelly, Dr. Nicole Lapeyrouse, and Dr. Matthew Rex is licensed under a Creative Commons Attribution-NonCommercial-ShareAlike 4.0 International License, except where otherwise noted.

Share This Book