Chapter 11: Liquids and Solids
11.8 X-Ray Crystallography
Learning Outcomes
- Explain the use of X-ray diffraction measurements in determining crystalline structures
The size of the unit cell and the arrangement of atoms in a crystal may be determined from measurements of the diffraction of X-rays by the crystal, termed X-ray crystallography. Diffraction is the change in the direction of travel experienced by an electromagnetic wave when it encounters a physical barrier whose dimensions are comparable to those of the wavelength of the light. X-rays are electromagnetic radiation with wavelengths about as long as the distance between neighboring atoms in crystals (on the order of a few Å).
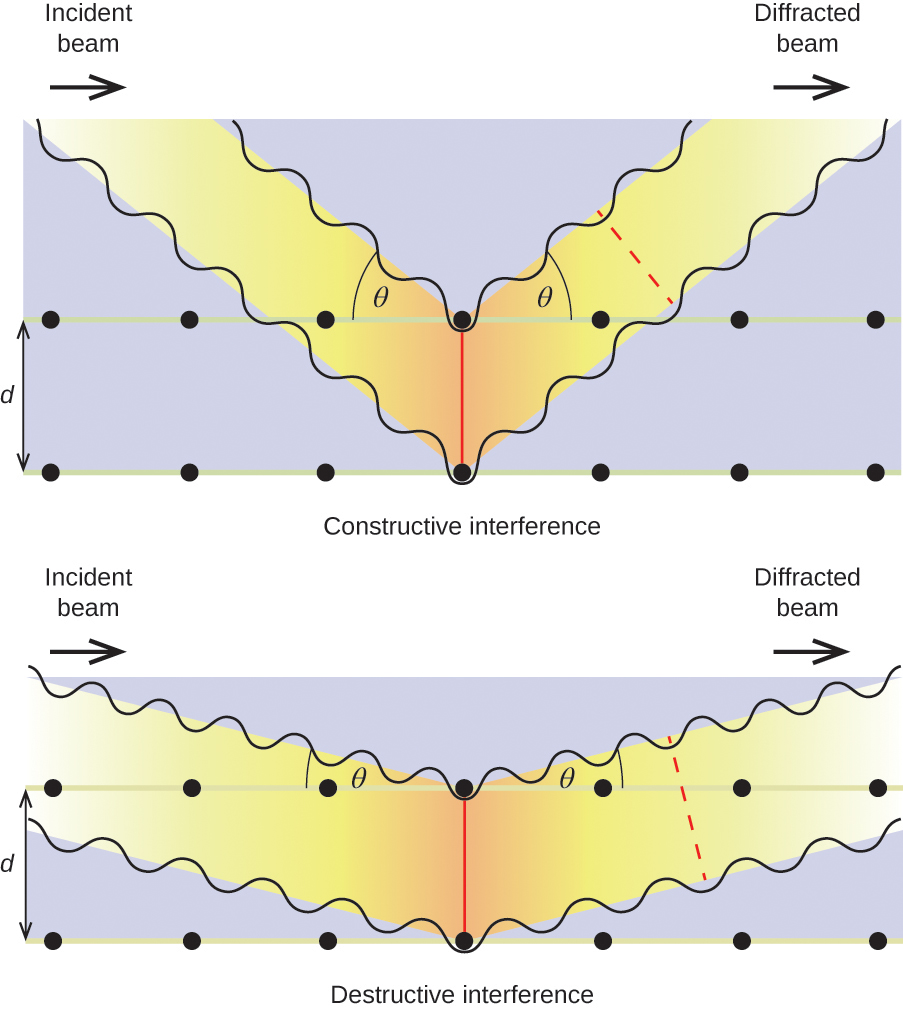
When a beam of monochromatic X-rays strikes a crystal, its rays are scattered in all directions by the atoms within the crystal. When scattered waves traveling in the same direction encounter one another, they undergo interference, a process by which the waves combine to yield either an increase or a decrease in amplitude (intensity) depending upon the extent to which the combining waves’ maxima are separated (see Figure 11.8.1).
When X-rays of a certain wavelength, [latex]\lambda[/latex], are scattered by atoms in adjacent crystal planes separated by a distance, d, they may undergo constructive interference when the difference between the distances traveled by the two waves prior to their combination is an integer factor, n, of the wavelength. This condition is satisfied when the angle of the diffracted beam, [latex]\theta[/latex], is related to the wavelength and interatomic distance by the equation:
[latex]n{\lambda }=2d\text{sin}\theta[/latex]
This relation is known as the Bragg equation in honor of W. H. Bragg, the English physicist who first explained this phenomenon. Figure 11.8.2 illustrates two examples of diffracted waves from the same two crystal planes. The figure on the left depicts waves diffracted at the Bragg angle, resulting in constructive interference, while that on the right shows diffraction and a different angle that does not satisfy the Bragg condition, resulting in destructive interference.
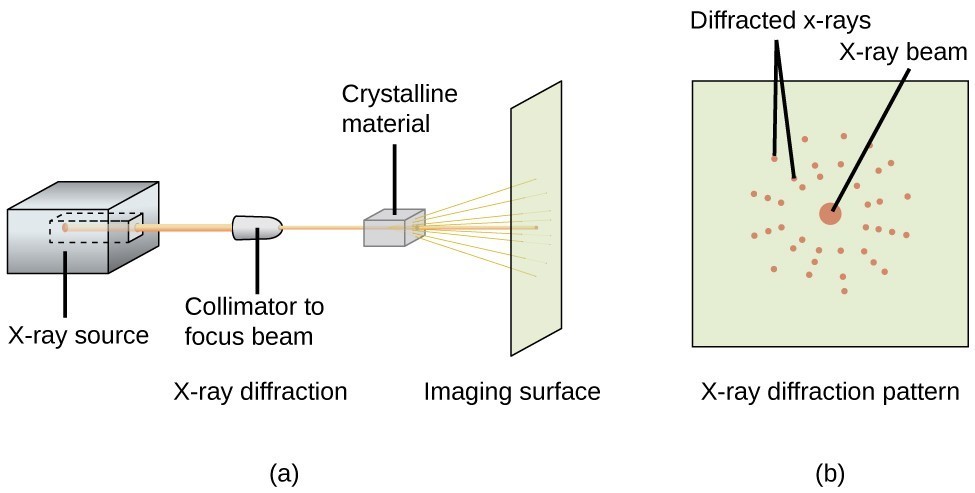
An X-ray diffractometer, such as the one illustrated in Figure 11.8.3, may be used to measure the angles at which X-rays are diffracted when interacting with a crystal as described above. From such measurements, the Bragg equation may be used to compute distances between atoms as demonstrated in the following example exercise.
Example 11.8.1: Using the Bragg Equation
In a diffractometer, X-rays with a wavelength of 0.1315 nm were used to produce a diffraction pattern for copper. The first order diffraction (n = 1) occurred at an angle [latex]\theta[/latex] = 25.25°. Determine the spacing between the diffracting planes in copper.
Show Solution
The distance between the planes is found by solving the Bragg equation, n[latex]\lambda[/latex] = 2d sin [latex]\theta[/latex], for d.
This gives: [latex]d=\dfrac{n\lambda}{2\sin\theta}=\dfrac{1\left(0.1315\text{ nm}\right)}{2\sin\left(25.25^{\circ}\right)}=0.154\text{ nm}[/latex]
Check Your Learning
Key Concepts and Summary
The type of structure and dimensions of the unit cell can be determined by X-ray diffraction measurements.
Key Equations
- [latex]n{\lambda }=2d\text{sin}\theta[/latex]
Try It
- What is the spacing between crystal planes that diffract X-rays with a wavelength of 1.541 nm at an angle [latex]\theta[/latex] of 15.55° (first order reflection)?
Show Selected Solutions
1. The Bragg equation is: n[latex]\lambda[/latex] = 2d sin [latex]\theta[/latex]
where d is the spacing between planes.
d = [latex]\frac{n{\lambda }}{\text{2 sin}\theta }=\frac{1(1.541 A)}{2\sin15.55^{\circ}}=\frac{1.541\mathring{\text{A}}}{2(0.2681)}[/latex] = 2.874 Å
Glossary
Bragg equation: equation that relates the angles at which X-rays are diffracted by the atoms within a crystal
diffraction: redirection of electromagnetic radiation that occurs when it encounters a physical barrier of appropriate dimensions
X-ray crystallography: experimental technique for determining distances between atoms in a crystal by measuring the angles at which X-rays are diffracted when passing through the crystal
experimental technique for determining distances between atoms in a crystal by measuring the angles at which X-rays are diffracted when passing through the crystal
redirection of electromagnetic radiation that occurs when it encounters a physical barrier of appropriate dimensions
equation that relates the angles at which X-rays are diffracted by the atoms within a crystal

