Chapter 12: Solutions and Colloids

Chapter 12 Practice

12.1 The Dissolution Process [Go to section 12.1]

  1. How do solutions differ from compounds? From other mixtures?
  2. Which of the principal characteristics of solutions can we see in the solutions of [latex]\ce{K2Cr2O7}[/latex] shown in Figure 12.1.1?
  3. When [latex]\ce{KNO3}[/latex] is dissolved in water, the resulting solution is significantly colder than the water was originally.
    1. Is the dissolution of [latex]\ce{KNO3}[/latex] an endothermic or an exothermic process?
    2. What conclusions can you draw about the intermolecular attractions involved in the process?
    3. Is the resulting solution an ideal solution?
  4. Give an example of each of the following types of solutions:
    1. a gas in a liquid
    2. a gas in a gas
    3. a solid in a solid
  5. Heat is released when some solutions form; heat is absorbed when other solutions form. Provide a molecular explanation for the difference between these two types of spontaneous processes.
Show Selected Solutions
  1. A solution can vary in composition, while a compound cannot vary in composition. Solutions are homogeneous at the molecular level, while other mixtures are heterogeneous.
  2. The answers are as follows:
    1. Endothermic
    2. Attraction between the [latex]\ce{K+}[/latex] and [latex]\ce{NO3-}[/latex] ions is stronger than between the ions and water molecules (the ion-ion interactions have a lower, more negative energy). Therefore, the dissolution process increases the energy of the molecular interactions, and it consumes the thermal energy of the solution to make up for the difference.
    3. No
  3. Heat is released when the total intermolecular forces (IMFs) between the solute and solvent molecules are stronger than the total IMFs in the pure solute and in the pure solvent: Breaking weaker IMFs and forming stronger IMFs releases heat. Heat is absorbed when the total IMFs in the solution are weaker than the total of those in the pure solute and in the pure solvent: Breaking stronger IMFs and forming weaker IMFs absorbs heat.


12.2 Electrolytes [Go to section 12.2]

  1. Explain why solutions of [latex]\ce{HBr}[/latex] in benzene (a non-polar solvent) are nonconductive, while solutions in water (a polar solvent) are conductive.
  2. Indicate the most important types of intermolecular attractions in each of the following solutions:
    1. The solution in Figure 12.1.1.
    2. [latex]\ce{O}(g)[/latex] in [latex]\ce{CO}(l)[/latex]
    3. [latex]\ce{Cl2}(g)[/latex] in [latex]\ce{Br2}(l)[/latex]
    4. [latex]\ce{HCl}(aq)[/latex] in benzene [latex]\ce{C6H6}(l)[/latex]
    5. Methanol [latex]\ce{CH3OH}(l)[/latex] in [latex]\ce{H2O}(l)[/latex]
  3. Compare the processes that occur when methanol ([latex]\ce{CH3OH}[/latex]), hydrogen chloride ([latex]\ce{HCl}[/latex]), and sodium hydroxide ([latex]\ce{NaOH}[/latex]) dissolve in water. Write equations and prepare sketches showing the form in which each of these compounds is present in its respective solution.
  4. Explain why the ions [latex]\ce{Na+}[/latex] and [latex]\ce{Cl−}[/latex] are strongly solvated in water but not in hexane, a solvent composed of non-polar molecules.
  5. Why are most solid ionic compounds electrically nonconductive, whereas aqueous solutions of ionic compounds are good conductors? Would you expect a liquid (molten) ionic compound to be electrically conductive or nonconductive? Explain.
  6. Consider the solutions presented:

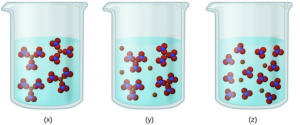
    1. Which of the following sketches best represents the ions in a solution of [latex]\ce{Fe(NO3)3}(aq)[/latex]?
    2. Write a balanced chemical equation showing the products of the dissolution of [latex]\ce{Fe(NO3)3}[/latex].
  7. What is the expected electrical conductivity of the following solutions?
    1. [latex]\ce{NaOH}(aq)[/latex]
    2. [latex]\ce{HCl}(aq)[/latex]
    3. [latex]\ce{C6H12O6}(aq)[/latex] (glucose)
    4. [latex]\ce{NH3(l)}[/latex]
  8. Indicate the most important type of intermolecular attraction responsible for solvation in each of the following solutions:
    1. the solutions in Figure 12.2.2
    2. methanol, [latex]\ce{CH3OH}[/latex], dissolved in ethanol, [latex]\ce{C2H5OH}[/latex]
    3. methane, [latex]\ce{CH4}[/latex], dissolved in benzene, [latex]\ce{C6H6}[/latex]
    4. the polar halocarbon [latex]\ce{CF2Cl2}[/latex] dissolved in the polar halocarbon [latex]\ce{CF2ClCFCl2}[/latex]
    5. [latex]\ce{O2}(l)[/latex] in [latex]\ce{N2}(l)[/latex]
Show Selected Solutions
  1. The answers are as follows:
    1. ion-dipole forces
    2. dipole-dipole forces
    3. dispersion forces
    4. dispersion forces
    5. hydrogen bonding
  2. Crystals of [latex]\ce{NaCl}[/latex] dissolve in water, a polar liquid with a very large dipole moment, and the individual ions become strongly solvated. Hexane is a non-polar liquid with a dipole moment of zero and, therefore, does not significantly interact with the ions of the [latex]\ce{NaCl}[/latex] crystals.
  3. The answers are as follows:
    1. [latex]\ce{Fe(NO3)3}[/latex] is a strong electrolyte, thus it should completely dissociate into [latex]\ce{Fe3+}[/latex] and ions. Therefore, (z) best represents the solution.
    2. [latex]\ce{Fe(NO3)3}(s) \rightarrow \ce{Fe^{3+}}(aq) + \ce{3NO3-}(aq)[/latex]
  4. The answers are as follows:
    1. ion-dipole
    2. hydrogen bonds
    3. dispersion forces
    4. dipole-dipole attractions
    5. dispersion forces

12.3 Types of Solutions and Solubility [Go to section 12.3]

  1. Suppose you are presented with a clear solution of sodium thiosulfate, [latex]\ce{Na2S2O3}[/latex]. How could you determine whether the solution is unsaturated, saturated, or supersaturated?
  2. Supersaturated solutions of most solids in water are prepared by cooling saturated solutions. Supersaturated solutions of most gases in water are prepared by heating saturated solutions. Explain the reasons for the difference in the two procedures.
  3. Suggest an explanation for the observations that ethanol, [latex]\ce{C2H5OH}[/latex], is completely miscible with water and that ethanethiol, [latex]\ce{C2H5SH}[/latex], is soluble only to the extent of 1.5 g per 100 mL of water.
  4. At 0 °C and 1.00 atm, as much as 0.70 g of [latex]\ce{O2}[/latex] can dissolve in 1 L of water. At 0 °C and 4.00 atm, how many grams of [latex]\ce{O2}[/latex] dissolve in 1 L of water?
  5. Which of the following gases is expected to be most soluble in water? Explain your reasoning.
    1. [latex]\ce{CH4}[/latex]
    2. [latex]\ce{CCl4}[/latex]
    3. [latex]\ce{CHCl3}[/latex]
  6. What mass of oxygen would be dissolved in a 6.604-gallon fish tank at 25 °C, at atmospheric pressure (1 atm). The partial pressure of [latex]\ce{O2}[/latex] at atmospheric pressure is about 0.21 atm. The Henry’s law constant for [latex]\ce{O2}[/latex] is 1.3 × 10-3M/atm at 25 °C.
  7. Refer to Figure 12.3.3.
    1. How did the concentration of dissolved [latex]\ce{CO2}[/latex] in the beverage change when the bottle was opened?
    2. What caused this change?
    3. Is the beverage unsaturated, saturated, or supersaturated with [latex]\ce{CO2}[/latex]?
Show Selected Solutions
  1. The solubility of solids usually decreases upon cooling a solution, while the solubility of gases usually decreases upon heating.
  2. 2.80 g
  3. 0.22 g

12.4 Solution Concentration [Go to section 12.4]

  1. How many liters of [latex]\ce{HCl}[/latex] gas, measured at 30.0 °C and 745 torr, are required to prepare 1.25 L of a 3.20-M solution of hydrochloric acid?
  2. Solutions of hydrogen in palladium may be formed by exposing [latex]\ce{Pd}[/latex] metal to [latex]\ce{H2}[/latex] gas. The concentration of hydrogen in the palladium depends on the pressure of [latex]\ce{H2}[/latex] gas applied, but in a more complex fashion than can be described by Henry’s law. Under certain conditions, 0.94 g of hydrogen gas is dissolved in 215 g of palladium metal.
    1. Determine the molarity of this solution (solution density = 1.8 g/cm3).
    2. Determine the molality of this solution (solution density = 1.8 g/cm3).
    3. Determine the percent by mass of hydrogen atoms in this solution (solution density = 1.8 g/cm3).
  3. Calculate the percent by mass of [latex]\ce{KBr}[/latex] in a saturated solution of [latex]\ce{KBr}[/latex] in water at 10 °C. See Figure 12.3.8 for useful data, and report the computed percentage to one significant digit.
  4. What are the mole fractions of [latex]\ce{H3PO4}[/latex] and water in a solution of 14.5 g of [latex]\ce{H3PO4}[/latex] in 125 g of water?
    1. Outline the steps necessary to answer the question.
    2. Answer the question.
  5. What are the mole fractions of [latex]\ce{HNO3}[/latex] and water in a concentrated solution of nitric acid (68.0% [latex]\ce{HNO3}[/latex] by mass)?
    1. Outline the steps necessary to answer the question.
    2. Answer the question.
  6. Calculate the mole fraction of each solute and solvent:
    1. 583 g of [latex]\ce{H2SO4}[/latex] in 1.50 kg of water—the acid solution used in an automobile battery
    2. 0.86 g of [latex]\ce{NaCl}[/latex] in 1.00 × 102 g of water—a solution of sodium chloride for intravenous injection
    3. 46.85 g of codeine, [latex]\ce{C18H21NO3}[/latex], in 125.5 g of ethanol, [latex]\ce{C2H5OH}[/latex]
    4. 25 g of I2 in 125 g of ethanol, [latex]\ce{C2H5OH}[/latex]
  7. What is the difference between a 1 M solution and a 1 m solution?
  8. Calculate the mole fractions of methanol, [latex]\ce{CH3OH}[/latex]; ethanol, [latex]\ce{C2H5OH}[/latex]; and water in a solution that is 40% methanol, 40% ethanol, and 20% water by mass. (Assume the data are good to two significant figures.)
  9. What is the molality of nitric acid in a concentrated solution of nitric acid (68.0% [latex]\ce{HNO3}[/latex] by mass)?
    1. Outline the steps necessary to answer the question.
    2. Answer the question.
  10. The concentration of glucose, [latex]\ce{C6H12O6}[/latex], in normal spinal fluid is [latex]\frac{75\text{mg}}{100\text{g}}[/latex]. What is the molality of the solution?
  11. A 13.0% solution of [latex]\ce{K2CO3}[/latex] by mass has a density of 1.09 g/cm3. Calculate the molality of the solution.
  12. Calculate the molality of each of the following solutions:
    1. 583 g of [latex]\ce{H2SO4}[/latex] in 1.50 kg of water—the acid solution used in an automobile battery
    2. 0.86 g of [latex]\ce{NaCl}[/latex] in 1.00 × 102 g of water—a solution of sodium chloride for intravenous injection
    3. 46.85 g of codeine, [latex]\ce{C18H21NO3}[/latex], in 125.5 g of ethanol, [latex]\ce{C2H5OH}[/latex]
    4. 25 g of [latex]\ce{I2}[/latex] in 125 g of ethanol, [latex]\ce{C2H5OH}[/latex]
  13. What is the molality of sulfuric acid, [latex]\ce{H2SO4}[/latex], in a solution containing10.2 g of [latex]\ce{H2SO4}[/latex] in 135 g of water?
Show Selected Solutions
  1. 102 L [latex]\ce{HCl}[/latex]
  2. 40%
  3. The answers are as follows:
    1. Determine the number of moles of each component. Then add the number of moles of components and divide that number into the moles of the component whose percentage is desired
    2. [latex]\ce{X_{H3PO4}}[/latex] = 0.0209, [latex]\ce{X_{H2O}}[/latex] = 0.979
  4. In a 1 M solution, the mole is contained in exactly 1 L of solution. In a 1 m solution, the mole is contained in exactly 1 kg of solvent.
  5. The answers are as follows:
    1. Determine the molar mass of [latex]\ce{HNO3}[/latex]. Determine the number of moles of acid in the solution. From the number of moles and the mass of solvent, determine the molality.
    2. 33.7 m
  6. 1.08 m
  7. 0.771 m

12.5 Colligative Properties [Go to section 12.5] & 12.6 Colligative Properties of Electrolyte Solutions [Go to section 12.6]

  1.  Why does 1 mol of sodium chloride depress the freezing point of 1 kg of water almost twice as much as 1 mol of glycerin?
  2. Assuming ideal solution behavior, what is the boiling point of a solution of 115.0 g of nonvolatile sucrose, [latex]\ce{C_{12}H_{22}O_{11}}[/latex], in 350.0 g of water?
    1. Outline the steps necessary to answer the question
    2. Answer the question
  3. Assuming ideal solution behavior, what is the boiling point of a solution of 9.04 g of [latex]\ce{I2}[/latex] in 75.5 g of benzene, assuming the [latex]\ce{I2}[/latex] is nonvolatile?
    1. Outline the steps necessary to answer the question.
    2. Answer the question.
  4. Assuming ideal solution behavior, what is the freezing temperature of a solution of 115.0 g of sucrose, [latex]\ce{C_{12}H_{22}O_{11}}[/latex], in 350.0 g of water?
    1. Outline the steps necessary to answer the question.
    2. Answer the question.
  5. Assuming ideal solution behavior, what is the freezing point of a solution of 9.04 g of [latex]\ce{I2}[/latex] in 75.5 g of benzene?
    1. Outline the steps necessary to answer the following question.
    2. Answer the question.
  6. Assuming ideal solution behavior, what is the osmotic pressure of an aqueous solution of 1.64 g of [latex]\ce{Ca(NO3)2}[/latex] in water at 25 °C? The volume of the solution is 275 mL.
    1. Outline the steps necessary to answer the question.
    2. Answer the question.
  7. Assuming ideal solution behavior, what is osmotic pressure of a solution of bovine insulin (molar mass, 5700 g mol[latex]^{–1}[/latex]) at 18 °C if 100.0 mL of the solution contains 0.103 g of the insulin?
    1. Outline the steps necessary to answer the question.
    2. Answer the question.
  8. Assuming ideal solution behavior, what is the molar mass of a solution of 5.00 g of a compound in 25.00 g of carbon tetrachloride (bp 76.8 °C; Kb = 5.02 °C/m) that boils at 81.5 °C at 1 atm?
    1. Outline the steps necessary to answer the question.
    2. Solve the problem.
  9. A sample of an organic compound (a non-electrolyte) weighing 1.35 g lowered the freezing point of 10.0 g of benzene by 3.66 °C. Assuming ideal solution behavior, calculate the molar mass of the compound.
  10. A 1.0 m solution of [latex]\ce{HCl}[/latex] in benzene has a freezing point of 0.4 °C. Is [latex]\ce{HCl}[/latex] an electrolyte in benzene? Explain.
  11. A solution contains 5.00 g of urea, [latex]\ce{CO(NH2)2}[/latex], a nonvolatile compound, dissolved in 0.100 kg of water. If the vapor pressure of pure water at 25 °C is 23.7 torr, what is the vapor pressure of the solution (assuming ideal solution behavior)?
  12. A 12.0-g sample of a nonelectrolyte is dissolved in 80.0 g of water. The solution freezes at –1.94 °C. Assuming ideal solution behavior, calculate the molar mass of the substance.
  13. Arrange the following solutions in order by their decreasing freezing points: 0.1 m [latex]\ce{Na3PO4}, 0.1 m \text{ } \ce{C2H5OH}, 0.01 m \text{ } \ce{CO2}, 0.15 m \text{ } \ce{NaCl}, \text{ and } 0.2 m \text{ } \ce{CaCl2}[/latex].
  14. Calculate the boiling point elevation of 0.100 kg of water containing 0.010 mol of [latex]\ce{NaCl}[/latex], 0.020 mol of [latex]\ce{Na2SO4}[/latex], and 0.030 mol of [latex]\ce{MgCl2}[/latex], assuming complete dissociation of these electrolytes and ideal solution behavior.
  15. How could you prepare a 3.08 m aqueous solution of glycerin, [latex]\ce{C3H8O3}[/latex]? Assuming ideal solution behavior, what is the freezing point of this solution?
  16. A sample of sulfur weighing 0.210 g was dissolved in 17.8 g of carbon disulfide, [latex]\ce{CS2}[/latex] (Kb = 2.34 °C/m). If the boiling point elevation was 0.107 °C, what is the formula of a sulfur molecule in carbon disulfide (assuming ideal solution behavior)?
  17. In a significant experiment performed many years ago, 5.6977 g of cadmium iodide in 44.69 g of water raised the boiling point 0.181 °C. What does this suggest about the nature of a solution of [latex]\ce{CdI2}[/latex]?
  18. Lysozyme is an enzyme that cleaves cell walls. A 0.100-L sample of a solution of lysozyme that contains 0.0750 g of the enzyme exhibits an osmotic pressure of 1.32 × 10–3 atm at 25 °C. Assuming ideal solution behavior, what is the molar mass of lysozyme?
  19. The osmotic pressure of a solution containing 7.0 g of insulin per liter is 23 torr at 25 °C. Assuming ideal solution behavior, what is the molar mass of insulin?
  20. The osmotic pressure of human blood is 7.6 atm at 37 °C. What mass of glucose, [latex]\ce{C6H_{12}O6}[/latex], is required to make 1.00 L of aqueous solution for intravenous feeding if the solution must have the same osmotic pressure as blood at body temperature, 37 °C (assuming ideal solution behavior)?
  21. Assuming ideal solution behavior, what is the freezing point of a solution of dibromobenzene, [latex]\ce{C6H4Br2}[/latex], in 0.250 kg of benzene, if the solution boils at 83.5 °C?
  22. Assuming ideal solution behavior, what is the boiling point of a solution of [latex]\ce{NaCl}[/latex] in water if the solution freezes at –0.93 °C?
  23. The sugar fructose contains 40.0% [latex]\ce{C}[/latex], 6.7% [latex]\ce{H}[/latex], and 53.3% [latex]\ce{O}[/latex] by mass. A solution of 11.7 g of fructose in 325 g of ethanol has a boiling point of 78.59 °C. The boiling point of ethanol is 78.35 °C, and Kb for ethanol is 1.20 °C/m. Assuming ideal solution behavior, what is the molecular formula of fructose?
  24. The vapor pressure of methanol, [latex]\ce{CH3OH}[/latex], is 94 torr at 20 °C. The vapor pressure of ethanol, [latex]\ce{C2H5OH}[/latex], is 44 torr at the same temperature.
    1. Calculate the mole fraction of methanol and of ethanol in a solution of 50.0 g of methanol and 50.0 g of ethanol.
    2. Ethanol and methanol form a solution that behaves like an ideal solution. Calculate the vapor pressure of methanol and of ethanol above the solution at 20 °C.
    3. Calculate the mole fraction of methanol and of ethanol in the vapor above the solution.
  25. The triple point of air-free water is defined as 273.16 K. Why is it important that the water be free of air?
  26. Meat can be classified as fresh (not frozen) even though it is stored at −1 °C. Why wouldn’t meat freeze at this temperature?
  27. An organic compound has a composition of 93.46% [latex]\ce{C}[/latex] and 6.54% [latex]\ce{H}[/latex] by mass. A solution of 0.090 g of this compound in 1.10 g of camphor melts at 158.4 °C. The melting point of pure camphor is 178.4 °C. Kf for camphor is 37.7 °C/m. Assuming ideal solution behavior, what is the molecular formula of the solute? Show your calculations.
  28. A sample of [latex]\ce{HgCl2}[/latex] weighing 9.41 g is dissolved in 32.75 g of ethanol, [latex]\ce{C2H5OH}[/latex] (Kb = 1.20 °C/m). The boiling point elevation of the solution is 1.27 °C. Is [latex]\ce{HgCl2}[/latex] an electrolyte in ethanol? Show your calculations.
  29. A salt is known to be an alkali metal fluoride. A quick approximate determination of freezing point indicates that 4 g of the salt dissolved in 100 g of water produces a solution that freezes at about −1.4 °C. What is the formula of the salt? Show your calculations.
  30. A solution of potassium nitrate, an electrolyte, and a solution of glycerin ([latex]\ce{C3H5(OH)3}[/latex]), a non-electrolyte, both boil at 100.3 °C. What other physical properties of the two solutions are identical?
  31. In a significant experiment performed many years ago, 5.6977 g of cadmium iodide in 44.69 g of water raised the boiling point 0.181 °C. What does this suggest about the nature of a solution of [latex]\ce{CdI2}[/latex]?
Show Selected Solutions
  1. The answers are as follows:
    1. Determine the molar mass of sucrose; determine the number of moles of sucrose in the solution; convert the mass of solvent to units of kilograms; from the number of moles and the mass of solvent, determine the molality; determine the difference between the boiling point of water and the boiling point of the solution; determine the new boiling point.
    2. 100.5 °C
  2. The answers are as follows:
    1. Determine the molar mass of sucrose; determine the number of moles of sucrose in the solution; convert the mass of solvent to units of kilograms; from the number of moles and the mass of solvent, determine the molality; determine the difference between the freezing temperature of water and the freezing temperature of the solution; determine the new freezing temperature.
    2. -1.8 °C
  3. The answers are as follows:
    1. Determine the molar mass of [latex]\ce{Ca(NO3)2}[/latex]; determine the number of moles of [latex]\ce{Ca(NO3)2}[/latex] in the solution; determine the number of moles of ions in the solution; determine the molarity of ions, then the osmotic pressure.
    2. 2.67 atm
  4. The answers are as follows:
    1. Determine the molal concentration from the change in boiling point and Kb; determine the moles of solute in the solution from the molal concentration and mass of solvent; determine the molar mass from the number of moles and the mass of solute
    2. Molecular mass = 2.1 × 10[latex]^2[/latex] amu
  5. No. Pure benzene freezes at 5.5 °C, and so the observed freezing point of this solution is depressed by ΔTf = 5.5 – 0.4 = 5.1 °C. The value computed, assuming no ionization of [latex]\ce{HCl}[/latex], is ΔTf = (1.0 m)(5.14 °C/m) = 5.1 °C. Agreement of these values supports the assumption that [latex]\ce{HCl}[/latex] is not ionized.
  6. Molecular mass = 144 amu
  7. 0.870 °C
  8. [latex]\ce{S8}[/latex]
  9. Molecular mass = 1.39 × 104 amu.
  10. 54 g
  11. 100.26 °C
  12. The answers are as follows:
    1. Methanol: 0.590; Ethanol: 0.410
    2. Methanol: 55 torr; Ethanol: 18 torr
    3. Methanol: 0.75; Ethanol: 0.25
  13. The ions and compounds present in the water in the beef lower the freezing point of the beef below –1 °C.
  14. 1.27 °C The observed change equals the theoretical change; therefore, no dissociation occurs.
  15. Both form homogeneous solutions; their boiling point elevations are the same, as are their lowering of vapor pressures. Osmotic pressure and the lowering of the freezing point are also the same for both solutions.


License

Icon for the Creative Commons Attribution-NonCommercial-ShareAlike 4.0 International License

Chemistry Fundamentals Copyright © by Dr. Julie Donnelly, Dr. Nicole Lapeyrouse, and Dr. Matthew Rex is licensed under a Creative Commons Attribution-NonCommercial-ShareAlike 4.0 International License, except where otherwise noted.

Share This Book