Chapter 14: Fundamental Equilibrium Concepts

14.3 Shifting Equilibria: Le Châtelier’s Principle

Learning Outcomes

  • Describe the ways in which an equilibrium system can be stressed (temperature, volume, pressure, concentration)
  • Predict the response of a stressed equilibrium using Le Châtelier’s principle

A system at equilibrium is in a state of dynamic balance, with forward and reverse reactions taking place at equal rates. If an equilibrium system is subjected to a change in conditions that affects these reaction rates differently (a stress), then the rates are no longer equal and the system is not at equilibrium. The system will subsequently experience a net reaction in the direction of greater rate (a shift) that will re-establish the equilibrium. This phenomenon is summarized by Le Châtelier’s principle: if an equilibrium system is stressed, the system will experience a shift in response to the stress that re-establishes equilibrium.

Reaction rates are affected primarily by concentrations, as described by the reaction’s rate law, and temperature, as described by the Arrhenius equation. Consequently, changes in concentration and temperature are the two stresses that can shift an equilibrium.

Effect of a Change in Concentration

If an equilibrium system is subjected to a change in the concentration of a reactant or product species, the rate of either the forward or the reverse reaction will change. As an example, consider the equilibrium reaction

[latex]\ce{H2}(g) + \ce{I2}(g) \rightleftharpoons \ce{2HI}(g)[/latex] [latex]K_c = 50.0 \text{at} 400 ^{\circ} C[/latex]

The rate laws for the forward and reverse reactions are

forward [latex]\ce{H2}(g) + \ce{I2}(g) \rightleftharpoons \ce{2HI}(g)[/latex] [latex]\text{rate}_f = k_f[\ce{H2}]^m[\ce{I2}]^n[/latex]

reverse [latex]\ce{2HI}(g) \rightleftharpoons \ce{H2}(g) + \ce{I2}(g)[/latex] [latex]\text{rate}_r = k_r[\ce{HI}]^x[/latex]

When this system is at equilibrium, the forward and reverse reaction rates are equal.

ratef = rater

If the system is stressed by adding reactant, either [latex]\ce{H2}[/latex] or [latex]\ce{I2}[/latex], the resulting increase in concentration causes the rate of the forward reaction to increase, exceeding that of the reverse reaction:

ratef > rater

The system will experience a temporary net reaction in the forward direction to re-establish equilibrium (the equilibrium will shift right). This same shift will result if some product [latex]\ce{HI}[/latex] is removed from the system, which decreases the rate of the reverse reaction, again resulting in the same imbalance in rates.

The same logic can be used to explain the left shift that results from either removing reactant or adding product to an equilibrium system. These stresses both result in an increased rate for the reverse reaction

ratef < rater

and a temporary net reaction in the reverse direction to re-establish equilibrium.

As an alternative to this kinetic interpretation, the effect of changes in concentration on equilibria can be rationalized in terms of reaction quotients. When the system is at equilibrium,

[latex]Q_c = \dfrac{\ce{[HI]}^2}{\ce{[H2]}}{\ce{[I2]}} = K_c[/latex]

If reactant is added (increasing the denominator of the reaction quotient) or product is removed (decreasing the numerator), then Qc < Kc and the equilibrium will shift right. Note that the three different ways of inducing this stress result in three different changes in the composition of the equilibrium mixture. If [latex]\ce{H2}[/latex] is added, the right shift will consume [latex]\ce{I2}[/latex] and produce HI as equilibrium is re-established, yielding a mixture with a greater concentrations of [latex]\ce{H2}[/latex] and [latex]\ce{HI}[/latex] and a lesser concentration of [latex]\ce{I2}[/latex] than was present before. If [latex]\ce{I2}[/latex] is added, the new equilibrium mixture will have greater concentrations of [latex]\ce{I2}[/latex] and [latex]\ce{HI}[/latex] and a lesser concentration of [latex]\ce{H2}[/latex]. Finally, if HI is removed, the concentrations of all three species will be lower when equilibrium is reestablished. Despite these differences in composition, the value of the equilibrium constant will be the same after the stress as it was before (per the law of mass action). The same logic may be applied for stresses involving removing reactants or adding product, in which case Qc > Kc and the equilibrium will shift left.

Effect of a Change in Volume (or Pressure)

For gas-phase equilibria such as this one, some additional perspectives on changing the concentrations of reactants and products are worthy of mention. The partial pressure P of an ideal gas is proportional to its molar concentration M,

[latex]M = \dfrac{n}{V} = \dfrac{P}{RT}[/latex]

and so changes in the partial pressures of any reactant or product are essentially changes in concentrations and thus yield the same effects on equilibria. Aside from adding or removing reactant or product, the pressures (concentrations) of species in a gas-phase equilibrium can also be changed by changing the volume occupied by the system. Since all species of a gas-phase equilibrium occupy the same volume, a given change in volume will cause the same change in concentration for both reactants and products. In order to discern what shift, if any, this type of stress will induce the stoichiometry of the reaction must be considered.

At equilibrium, the reaction [latex]\ce{H2}(g) + \ce{I2}(g) \rightleftharpoons \ce{2HI}(g)[/latex] is described by the reaction quotient

[latex]Q_p = \dfrac{P_\text{HI}^2}{P_{\text{H}_2}P_{\text{I}_2}} = K_p[/latex]

If the volume occupied by an equilibrium mixture of these species is decreased by a factor of 3, the partial pressures of all three species will be increased by a factor of 3:

[latex]Q_{p} \text{ }^{'} = \dfrac{(3P_\ce{HI})^2}{3P_{\ce{H}_2}3P_{\ce{I}_2}} = \dfrac{(9P_\ce{HI})^2}{9P_{\ce{H}_2}P_{\text{I}_2}} = \dfrac{(P_\ce{HI})^2}{P_{\ce{H}_2}P_{\ce{I}_2}} = Q_p = K_p[/latex]

[latex]Q_{p} \text{ }^{'} = Q_p = K_p[/latex]

And so, changing the volume of this gas-phase equilibrium mixture does not results in a shift of the equilibrium.

A similar treatment of a different system, [latex]\ce{2NO2} (g) \rightleftharpoons \ce{2NO}(g) + \ce{O2}(g)[/latex], however, yields a different result:

[latex]Q_p = \dfrac{P_\ce{NO}2P_{\ce{O}_2}}{P_{\ce{NO}_2}2}[/latex]

[latex]Q_p \text{ }^{'} = \dfrac{(3P_\ce{NO})^23P_{\ce{O}_2}}{(3P_{\ce{NO}_2})^2} = \dfrac{9P_\ce{NO}23P_{\ce{O}_2}}{9P_{\ce{NO}_2}2} = \dfrac{27P_\ce{NO}2P_{\ce{O}_2}}{9P_{\ce{NO}_2}2} = 3Q_p > K_p[/latex]

[latex]Q_p \text{ }^{'} = 3Q_p > K_p[/latex]

In this case, the change in volume results in a reaction quotient greater than the equilibrium constant, and so the equilibrium will shift left.

These results illustrate the relationship between the stoichiometry of a gas-phase equilibrium and the effect of a volume-induced pressure (concentration) change. If the total molar amounts of reactants and products are equal, as in the first example, a change in volume does not shift the equilibrium. If the molar amounts of reactants and products are different, a change in volume will shift the equilibrium in a direction that better “accommodates” the volume change. In the second example, two moles of reactant ([latex]\ce{NO2}[/latex]) yield three moles of product ([latex]\ce{2NO + O2}[/latex]), and so decreasing the system volume causes the equilibrium to shift left since the reverse reaction produces less gas (2 mol) than the forward reaction (3 mol). Conversely, increasing the volume of this equilibrium system would result in a shift towards products.

Effect of Change in Temperature on Equilibrium

Consistent with the law of mass action, an equilibrium stressed by a change in concentration will shift to re-establish equilibrium without any change in the value of the equilibrium constant, K. When an equilibrium shifts in response to a temperature change, however, it is re-established with a different relative composition that exhibits a different value for the equilibrium constant.

To understand this phenomenon, consider the elementary reaction

[latex]\text{A} \rightleftharpoons \text{B}[/latex]

Since this is an elementary reaction, the rates laws for the forward and reverse may be derived directly from the balanced equation’s stoichiometry:

ratef = kf[A]

rater = kr[B]

When the system is at equilibrium,

rater = ratef

Substituting the rate laws into this equality and rearranging gives

kf[A] = kr[B]

[latex]\dfrac{[\text{B}]}{[\text{A}]} = \dfrac{k_f}{k_r} = K_c[/latex]

The equilibrium constant is seen to be a mathematical function of the rate constants for the forward and reverse reactions. Since the rate constants vary with temperature as described by the Arrhenius equation, is stands to reason that the equilibrium constant will likewise vary with temperature (assuming the rate constants are affected to different extents by the temperature change). For more complex reactions involving multistep reaction mechanisms, a similar but more complex mathematical relation exists between the equilibrium constant and the rate constants of the steps in the mechanism. Regardless of how complex the reaction may be, the temperature-dependence of its equilibrium constant persists.

Predicting the shift an equilibrium will experience in response to a change in temperature is most conveniently accomplished by considering the enthalpy change of the reaction. For example, the decomposition of dinitrogen tetroxide is an endothermic (heat-consuming) process:

[latex]\ce{N2O4}(g) \rightleftharpoons \ce{2NO2}(g)[/latex] [latex]\Delta H = +57.20 kJ[/latex]

For purposes of applying Le Chatelier’s principle, heat (q) may be viewed as a reactant:

[latex]\text{heat} +\ce{N2O4}(g) \rightleftharpoons \ce{2NO2}(g)[/latex]

Raising the temperature of the system is akin to increasing the amount of a reactant, and so the equilibrium will shift to the right. Lowering the system temperature will likewise cause the equilibrium to shift left. For exothermic processes, heat is viewed as a product of the reaction and so the opposite temperature dependence is observed.

Catalysts Do Not Affect Equilibrium

The kinetics chapter of this text identifies a catalyst as a substance that enables a reaction to proceed via a different mechanism with an accelerated rate. The catalyzed reaction mechanism involves a lower energy transition state than the uncatalyzed reaction, resulting in a lower activation energy, Ea, and a correspondingly greater rate constant.

To discern the effect of catalysis on an equilibrium system, consider the reaction diagram for a simple one-step (elementary) reaction shown in Figure 14.3.1. The lowered transition state energy of the catalyzed reaction results in lowered activation energies for both the forward and the reverse reactions. Consequently, both forward and reverse reactions are accelerated, and equilibrium is achieved more quickly but without a change in the equilibrium constant.
A graph is shown labeled “Transition state.” The y-axis on the graph is labeled “Energy” and the x-axis is labeled “Extent of Reaction.” Two curves are plotted on the graph. Both start mid-way up the y-axis. The red curve has a steep initial slope as it increases, then reaches its peak where it meets a horizontal dotted line, then has a steep decline before leveling out. From the initial point to the horizontal line, there is a vertical line with arrows on each end labeled “E subscript a forward.” From the end point to the horizontal line, there is a vertical line with arrows on each end labeled “E subscript a reverse.” The second curve is less steep than the first and does not reach as high of a peak on the y-axis. It meets a separate horizontal dotted line at its peak, then declines at a similar rate to the first curve before leveling out with the first curve. From the initial point where the slope begins to increase to the horizontal line, there is a vertical line with arrows on each end labeled “E subscript a forward.” From the end point right as it levels out to the horizontal line, there is a vertical line with arrows on each end labeled “E subscript a reverse.”
Figure 14.3.1. Reaction diagrams for an elementary process in the absence (red) and presence (blue) of a catalyst. The presence of catalyst lowers the activation energies of both the forward and reverse reactions but does not affect the value of the equilibrium constant.

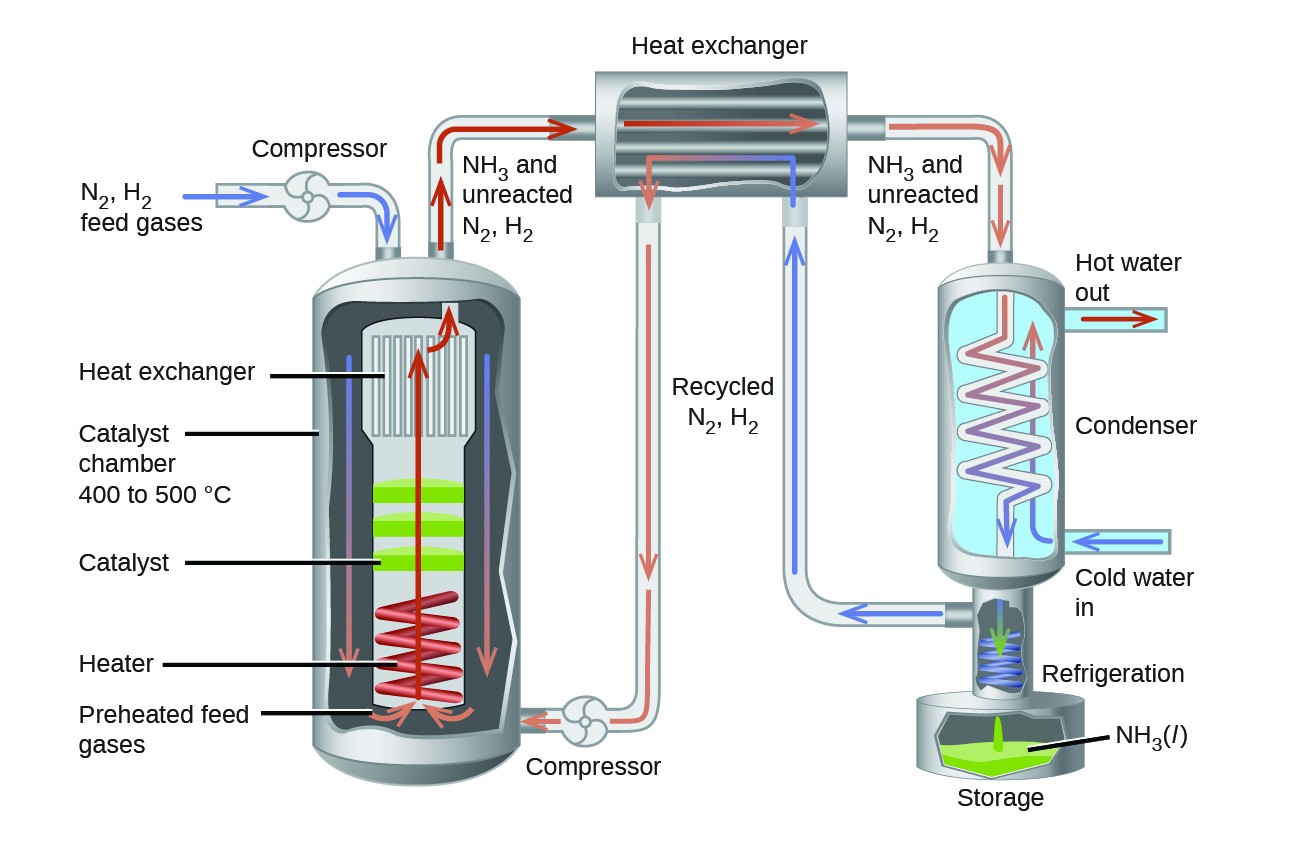
An interesting case study highlighting these equilibrium concepts is the industrial production of ammonia, NH3. This substance is among the “top 10” industrial chemicals with regard to production, with roughly two billion pounds produced annually in the US. Ammonia is used as a chemical feedstock to synthesize a wide range of commercially useful compounds, including fertilizers, plastics, dyes, and explosives.

Most industrial production of ammonia uses the Haber-Bosch process based on the following equilibrium reaction:

[latex]\ce{N2}\left(g\right)+\ce{3H2}\left(g\right)\rightleftharpoons\ce{2NH3}\left(g\right)[/latex] [latex]\Delta H = -92.2 kJ[/latex]

The traits of this reaction present challenges to its use in an efficient industrial process. The equilibrium constant is relatively small (Kp on the order of 10−5 at 25 °C), meaning very little ammonia is present in an equilibrium mixture. Also, the rate of this reaction is relatively slow at low temperatures. To raise the yield of ammonia, the industrial process is designed to operate under conditions favoring product formation:

  • High pressures (concentrations) of reactants are used, ~150−250 atm, to shift the equilibrium right, favoring product formation.
  • Ammonia is continually removed (collected) from the equilibrium mixture during the process, lowering its concentration and also shifting the equilibrium right.
  • Although low temperatures favor product formation for this exothermic process, the reaction rate at low temperatures is inefficiently slow. A catalyst is used to accelerate the reaction to reasonable rates at relatively moderate temperatures (400−500 °C).

A diagram illustrating a typical industrial setup for production of ammonia via the Haber-Bosch process is shown in Figure 14.3.2.

A diagram is shown that is composed of three main sections. The first section shows an intake pipe labeled with blue arrows and the terms, “N subscript 2, H subscript 2, feed gases,” and “Compressor.” This pipe leads to a large chamber with a turbine in the top section and a coil in the bottom section. From top to bottom, the sections of this chamber are labeled, “Heat exchanger,” “Catalyst chamber 400 to 500 degrees C,” “Catalyst,” “Heater,” and “Preheated feed gases.” One pipe leads from the top of this chamber with red arrows and is labeled, “N H subscript 3 and unreacted N subscript 2, H subscript 2,” while another pipe leads to the bottom of the chamber and reads, “Compressor,” and has orange arrows going through it. These two pipes are connected to a square container that is labeled, “Heat exchanger,” and has red arrows going into it from the upper pipe, orange arrows going away from it to the lower pipe and into a third system. The pipes leading into and out of the heat exchanger are labeled, “Recycled N subscript 2, H subscript 2.” The third system shows a container with an interior zig-zag-shaped pipe that sits on a base that contains a curled pipe on a storage tank. From the top of the image to the bottom are the terms, “N H subscript 3 and unreacted N subscript 2, H subscript 2,” “Condenser,” “Cold water in,” “Refrigeration,” “N H subscript 3 ( l ),” and “Storage” Blue arrows lead away from the base of this system and into the second system while other blue arrows lead into the system from the right side of the diagram and back out of the same chamber.
Figure 14.3.2. The figure shows a typical industrial setup for the commercial production of ammonia by the Haber-Bosch process. The process operates under conditions that stress the chemical equilibrium to favor product formation.

Key Concepts and Summary

Systems at equilibrium can be disturbed by changes to temperature, concentration, and, in some cases, volume and pressure. The system’s response to these disturbances is described by Le Châtelier’s principle: An equilibrium system subjected to a disturbance will shift in a way that counters the disturbance and re-establishes equilibrium. A catalyst will increase the rate of both the forward and reverse reactions of a reversible process, increasing the rate at which equilibrium is reached but not altering the equilibrium mixture’s composition (K does not change).

Table 14.3.1. Effects of Disturbances of Equilibrium and K
Disturbance Observed Change as Equilibrium is Restored Direction of Shift Effect on K
reactant added added reactant is partially consumed toward products none
product added added product is partially consumed toward reactants none
decrease in volume/increase in gas pressure pressure decreases toward side with fewer moles of gas none
increase in volume/decrease in gas pressure pressure increases toward side with fewer moles of gas none
temperature increase heat is absorbed toward products for endothermic, toward reactants for exothermic changes
temperature decrease heat is given off toward reactants for endothermic, toward products for exothermic changes

Try It

  1. Nitrogen and oxygen react at high temperatures.
    1. Write the expression for the equilibrium constant (Kc) for the reversible reaction
      [latex]\ce{N2}\left(g\right)+\ce{O2}\left(g\right)\rightleftharpoons\ce{2NO}\left(g\right)\Delta H=181\text{kJ}[/latex]
    2. What will happen to the concentrations of [latex]\ce{N2}[/latex], [latex]\ce{O2}[/latex], and [latex]\ce{NO}[/latex] at equilibrium if (i) more [latex]\ce{O2}[/latex] is added?
    3. What will happen to the concentrations of [latex]\ce{N2}[/latex], [latex]\ce{O2}[/latex], and [latex]\ce{NO}[/latex] at equilibrium if [latex]\ce{N2}[/latex] is removed?
    4. What will happen to the concentrations of [latex]\ce{N2}[/latex], [latex]\ce{O2}[/latex], and [latex]\ce{NO}[/latex] at equilibrium if [latex]\ce{NO}[/latex] is added?
    5. What will happen to the concentrations of [latex]\ce{N2}[/latex], [latex]\ce{O2}[/latex], and [latex]\ce{NO}[/latex] at equilibrium if the pressure on the system is increased by reducing the volume of the reaction vessel?
    6. What will happen to the concentrations of [latex]\ce{N2}[/latex], [latex]\ce{O2}[/latex], and [latex]\ce{NO}[/latex] at equilibrium if the temperature of the system is increased?

What will happen to the concentrations of [latex]\ce{N2}[/latex], [latex]\ce{O2}[/latex], and NO at equilibrium if a catalyst is added?

Show Selected Solutions

Glossary

Le Châtelier’s principle: when a chemical system at equilibrium is disturbed, it returns to equilibrium by counteracting the disturbance

position of equilibrium: concentrations or partial pressures of components of a reaction at equilibrium (commonly used to describe conditions before a disturbance)

stress: change to a reaction’s conditions that may cause a shift in the equilibrium

Licenses and Attributions (Click to expand)

CC licensed content, Shared previously

  • Chemistry 2e. Provided by: OpenStax. Located at: https://openstax.org/. License: CC BY: Attribution. License Terms: Access for free at
    https://openstax.org/books/chemistry-2e/pages/1-introduction

All rights reserved content

  • Volume Effect on Equilibrium – LeChatelier’s Principle Lab Extension. Authored by: North Carolina School of Science and Mathematics. Located at: https://youtu.be/pnU7ogsgUW8. License: Other. License Terms: Standard YouTube License
  • Le Chatelier’s Principle. Authored by: Professor Dave Explains. Located at: https://youtu.be/XmgRRmxS3is. License: Other. License Terms: Standard YouTube License
definition

License

Icon for the Creative Commons Attribution-NonCommercial-ShareAlike 4.0 International License

Chemistry Fundamentals Copyright © by Dr. Julie Donnelly, Dr. Nicole Lapeyrouse, and Dr. Matthew Rex is licensed under a Creative Commons Attribution-NonCommercial-ShareAlike 4.0 International License, except where otherwise noted.

Share This Book