4.4 Ionization energy and Electron Affinity

https://chem.libretexts.org/Bookshelves/General_Chemistry/Map%3A_A_Molecular_Approach_(Tro)/08%3A_Periodic_Properties_of_the_Elements/8.08%3A_Electron_Affinities_and_Metallic_Character

Ionization Energy

The amount of energy required to remove the most loosely bound electron from a gaseous atom in its ground state is called its first ionization energy (IS₁). The first ionization energy for an element, X, is the energy required to form a cation with +1 charge:

[latex]\text{X}\left(g\right)\longrightarrow {\text{X}}^{\text{+}}\left(g\right)+{\text{e}}^{-}{\text{IE}}_{1}[/latex]

The energy required to remove the second most loosely bound electron is called the second ionization energy (IS₂).

[latex]\ce{X+}(g)\longrightarrow \ce{X^2+}(g)+\ce{e-IE2}[/latex]

The energy required to remove the third electron is the third ionization energy, and so on. Energy is always required to remove electrons from atoms or ions, so ionization processes are endothermic and IE values are always positive. For larger atoms, the most loosely bound electron is located farther from the nucleus and so is easier to remove. Thus, as size (atomic radius) increases, the ionization energy should decrease. Relating this logic to what we have just learned about radii, we would expect first ionization energies to decrease down a group and to increase across a period.

Figure 4.4.1 graphs the relationship between the first ionization energy and the atomic number of several elements. The values of first ionization energy for the elements are given in Figure 4.4.2. Within a period, the IS₁ generally increases with increasing Z. Down a group, the IS₁ value generally decreases with increasing Z. There are some systematic deviations from this trend, however. Note that the ionization energy of boron (atomic number 5) is less than that of beryllium (atomic number 4) even though the nuclear charge of boron is greater by one proton. This can be explained because the energy of the subshells increases as l increases, due to penetration and shielding (as discussed previously in this chapter). Within any one shell, the s electrons are lower in energy than the p electrons. This means that an s electron is harder to remove from an atom than a p electron in the same shell. The electron removed during the ionization of beryllium ([latex]\ce{[He]}2s^2[/latex]) is an s electron, whereas the electron removed during the ionization of boron ([latex]\ce{[He]}2s^22p^1[/latex]) is a p electron; this results in a lower first ionization energy for boron, even though its nuclear charge is greater by one proton. Thus, we see a small deviation from the predicted trend occurring each time a new subshell begins.

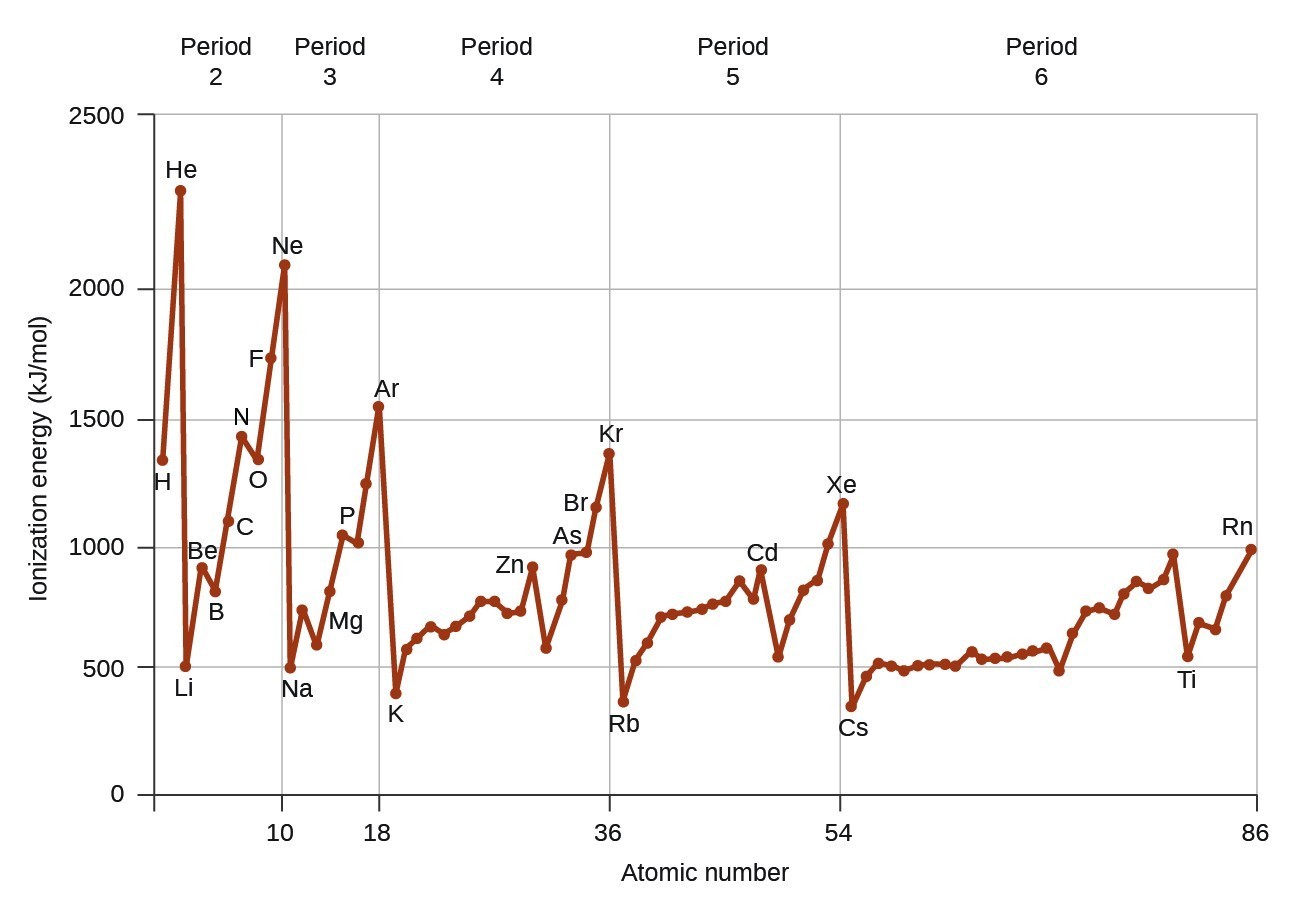
Another deviation occurs as orbitals become more than one-half filled. The first ionization energy for oxygen is slightly less than that for nitrogen, despite the trend in increasing IS₁ values across a period. Looking at the orbital diagram of oxygen, we can see that removing one electron will eliminate the electron–electron repulsion caused by pairing the electrons in the 2p orbital and will result in a half-filled orbital (which is energetically favorable). Analogous changes occur in succeeding periods (note the dip for sulfur after phosphorus in Figure 4.4.2).

Removing an electron from a cation is more difficult than removing an electron from a neutral atom because of the greater electrostatic attraction to the cation. Likewise, removing an electron from a cation with a higher positive charge is more difficult than removing an electron from an ion with a lower charge. Thus, successive ionization energies for one element always increase. As seen in Table 4.4.1, there is a large increase in the ionization energies (color change) for each element. This jump corresponds to removal of the core electrons, which are harder to remove than the valence electrons. For example, [latex]\ce{Sc}[/latex] and [latex]\ce{Ga}[/latex] both have three valence electrons, so the rapid increase in ionization energy occurs after the third ionization. This pattern explains why the chemistry of the elements normally involves only valence electrons. Too much energy is required to either remove or share the inner electrons.

Electron Affinity

The electron affinity (EA) of an element E is defined as the energy change that occurs when an electron is added to a gaseous atom or ion:

[latex]E_{(g)}+e^- \rightarrow E^-_{(g)} \;\;\;  \text{energy change=}EA \label{7.5.1}[/latex]

Unlike ionization energies, which are always positive for a neutral atom because energy is required to remove an electron, electron affinities can be negative (energy is released when an electron is added), positive (energy must be added to the system to produce an anion), or zero (the process is energetically neutral). This sign convention is consistent with a negative value corresponded to the energy change for an exothermic process, which is one in which heat is released (Figure 4.4.3).

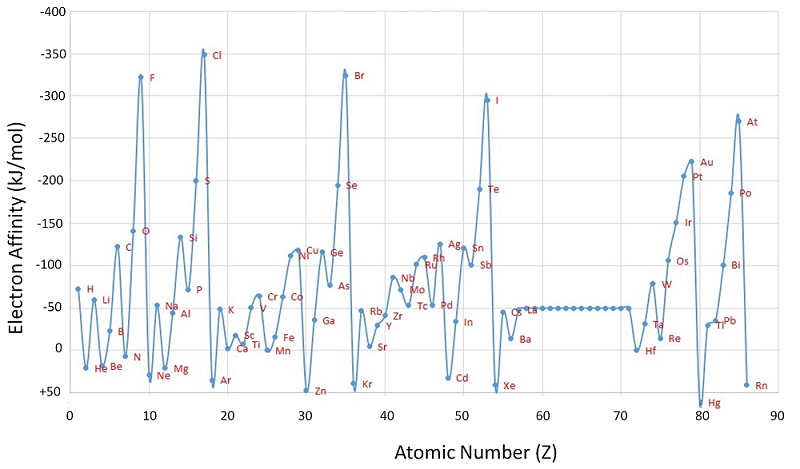
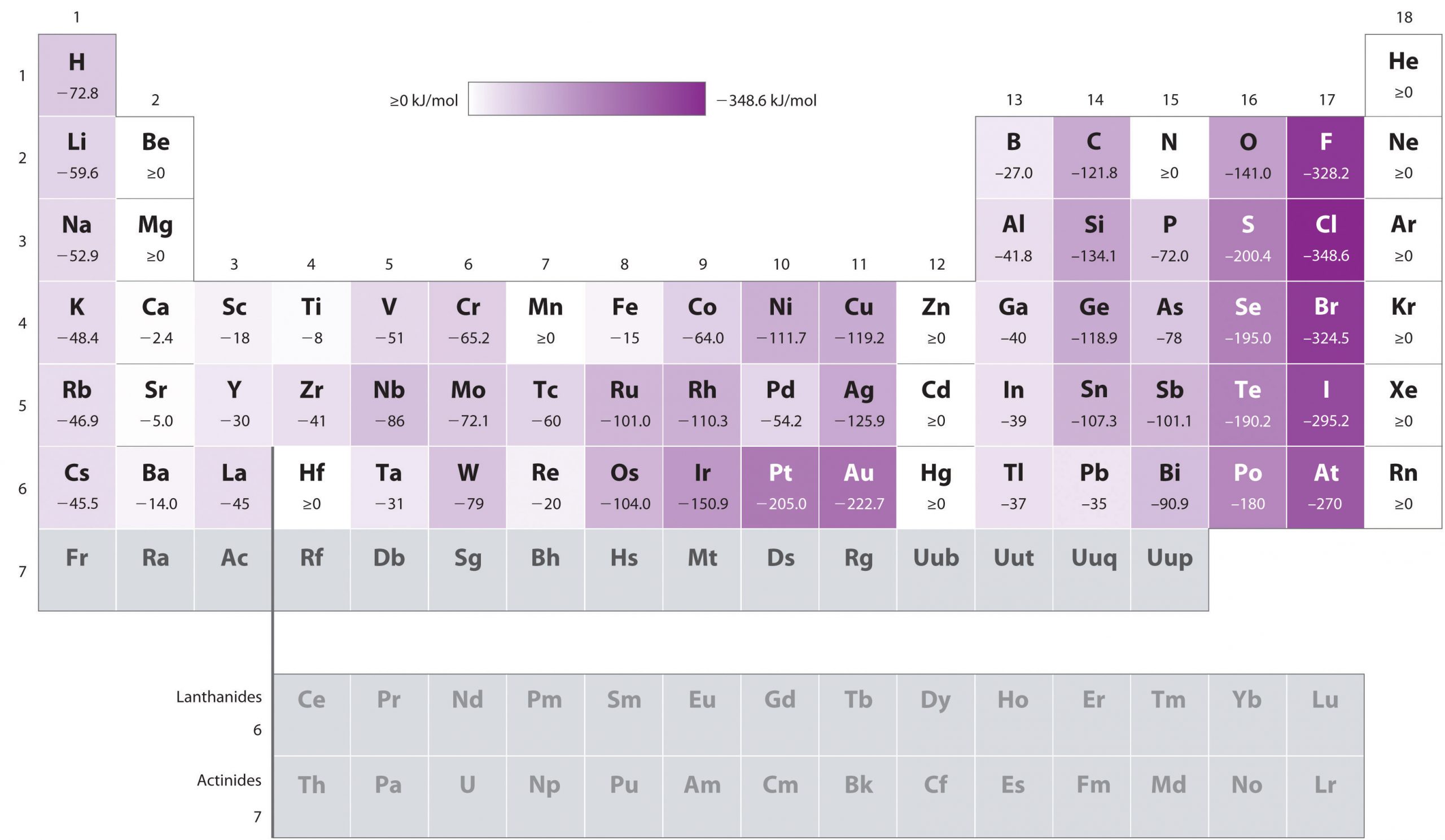
The chlorine atom has the most negative electron affinity of any element, which means that more energy is released when an electron is added to a gaseous chlorine atom than to an atom of any other element:

[latex]\ce{ Cl(g) + e^- \rightarrow Cl^- (g)} \;\;\;  EA=-346\; kJ/mol \label{7.5.2}[/latex]

In contrast, beryllium does not form a stable anion, so its effective electron affinity is

[latex]\ce{ Be(g) + e^- \rightarrow Be^- (g)} \;\;\;  EA \ge 0 \label{7.5.3}[/latex]

Nitrogen is unique in that it has an electron affinity of approximately zero. Adding an electron neither releases nor requires a significant amount of energy:

[latex]\ce{ N(g) + e^- \rightarrow N^- (g)} \;\;\;  EA \approx 0 \label{7.5.4}[/latex]

In general, electron affinities of the main-group elements become less negative as we proceed down a column. This is because as n increases, the extra electrons enter orbitals that are increasingly far from the nucleus.

Atoms with the largest radii, which have the lowest ionization energies (affinity for their own valence electrons), also have the lowest affinity for an added electron. There are, however, two major exceptions to this trend:

1. The electron affinities of elements [latex]\ce{B}[/latex] through [latex]\ce{F}[/latex] in the second row of the periodic table are less negative than those of the elements immediately below them in the third row. Apparently, the increased electron–electron repulsions experienced by electrons confined to the relatively small 2p orbitals overcome the increased electron–nucleus attraction at short nuclear distances. Fluorine, therefore, has a lower affinity for an added electron than does chlorine. Consequently, the elements of the third row (n = 3) have the most negative electron affinities. Farther down a column, the attraction for an added electron decreases because the electron is entering an orbital more distant from the nucleus. Electron–electron repulsions also decrease because the valence electrons occupy a greater volume of space. These effects tend to cancel one another, so the changes in electron affinity within a family are much smaller than the changes in ionization energy.
2. The electron affinities of the alkaline earth metals become more negative from [latex]\ce{Be}[/latex] to [latex]\ce{Ba}[/latex]. The energy separation between the filled ns² and the empty np subshells decreases with increasing n, so that formation of an anion from the heavier elements becomes energetically more favorable.

The equations for second and higher electron affinities are analogous to those for second and higher ionization energies:

[latex]E_{(g)} + e^- \rightarrow E^-_{(g)} \;\;\; \text{energy change=}EA_1 \label{7.5.5}[/latex]

[latex]E^-_{(g)} + e^- \rightarrow E^{2-}_{(g)} \;\;\; \text{energy change=}EA_2 \label{7.5.6}[/latex]

As we have seen, the first electron affinity can be greater than or equal to zero or negative, depending on the electron configuration of the atom. In contrast, the second electron affinity is always positive because the increased electron–electron repulsions in a dianion are far greater than the attraction of the nucleus for the extra electrons. For example, the first electron affinity of oxygen is −141 kJ/mol, but the second electron affinity is +744 kJ/mol:

[latex]\ce{O_{(g)}} + e^- \rightarrow \ce{O^-_{(g)}} \;\;\; EA_1=-141 \;kJ/mol \label{7.5.7}[/latex]

[latex]\ce{O^-_{(g)}} + e^- \rightarrow \ce{O^{2-}_{(g)}} \;\;\; EA_2=+744 \;kJ/mol \label{7.5.8}[/latex]

Thus the formation of a gaseous oxide ([latex]\ce{O^{2−}}[/latex]) ion is energetically quite unfavorable (estimated by adding both steps):

[latex]\ce{O_{(g)}} + 2e^- \rightarrow \ce{O^{2-}_{(g)}} \;\;\; EA=+603 \;kJ/mol \label{7.5.9}[/latex]

Similarly, the formation of all common dianions (such as [latex]\ce{S^{2−}}[/latex]) or trianions (such as [latex]\ce{P^{3−}}[/latex]) is energetically unfavorable in the gas phase.

If energy is required to form both positively charged cations and monatomic polyanions, why do ionic compounds such as [latex]\ce{MgO}[/latex], [latex]\ce{Na_2S}[/latex], and [latex]\ce{Na_3P}[/latex] form at all? The key factor in the formation of stable ionic compounds is the favorable electrostatic interactions between the cations and the anions in the crystalline salt.

Glossary

electron affinity: energy required to add an electron to a gaseous atom to form an anion

ionization energy: energy required to remove an electron from a gaseous atom or ion. The associated number (e.g., second ionization energy) corresponds to the charge of the ion produced (X²⁺)

https://chem.libretexts.org/Textbook…and_Metalloids