Chapter 14: Fundamental Equilibrium Concepts

Chapter 14 Practice

14.2 Equilibrium Constants [Go to section 14.2]

  1. For each of the following reactions, determine whether the value of the equilibrium constant favors the formation of reactants, products, or both sides equally.
    1. [latex]\ce{Br2}(g) + \ce{Cl2}(g) \leftrightarrow 2 \ce{BrCl}(g)[/latex] Keq = 3 × 106
    2. [latex]\ce{H2}(g) + \ce{Br2}(g) \leftrightarrow 2 \ce{HBr}[/latex](g) Keq = 1.15
    3. [latex]\ce{I2}(g) \leftrightarrow  \ce{I}(g) + \ce{I}[/latex](g) Keq = 4.5 × 10-7
  2. The following reaction occurs when a burner on a gas stove is lit: [latex]{\text{CH}}_{4}\left(g\right)+2{\text{O}}_{2}\left(g\right)\rightleftharpoons{\text{CO}}_{2}\left(g\right)+2{\text{H}}_{2}\text{O}\left(g\right)[/latex]
    Is an equilibrium among [latex]\ce{CH4, O2, CO2}[/latex], and [latex]\ce{H2O}[/latex] established under these conditions? Explain your answer.
  3. Molecular chlorine decomposes into atoms according to the reaction: [latex]\ce{Cl2} (g) \leftrightarrow 2 \ce{Cl}[/latex] (g)The equilibrium constant for the reaction at 25°C is 1.4 × 10-38. Would many chlorine atoms be present at this temperature? Explain how you can determine this.
Show Selected Solutions
  1. The answers are as follows:
    1. Products
    2. Both sides equally
    3. Reactants
  2. No, the equilibrium constant is quite small. When expressing the equilibrium constant, [latex]\frac{[\ce{Cl}]^2}{[\ce{Cl2}]}[/latex], for this to be such a small number the value in the numerator would need to be extremely small compared to the value in the denominator.


14.3 Shifting Equilibria: Le Châtelier’s Principle [Go to section 14.3]

  1. Chemical engineers use Le Chatêlier’s principle to predict shifts in chemical system at equilibrium resulting from changes in reaction conditions. Predict the changes needed to maximize the yield of product in each of the following industrial chemical systems:
    1. the production of ethene (ethylene) [latex]\ce{C2H6}(g) + \text{energy} \leftrightarrow \ce{C2H4}(g) + \ce{H2}(g)[/latex]
    2. the production of methanol [latex]\ce{CO}(g) + \ce{2H2}(g) \leftrightarrow \ce{CH3OH}(g)[/latex] + energy
  2. What property of a reaction can we use to predict the effect of a change in temperature on the value of an equilibrium constant?
  3. Examine the reaction, A [latex]\rightarrow[/latex] B ΔH = -100 kJ. In which direction (left or right) would the following stresses cause the system to shift?
    1. decrease the concentration of A
    2. increase the concentration of B
    3. lower the temperature
  4. A necessary step in the manufacture of sulfuric acid is the formation of sulfur trioxide, [latex]\ce{SO3}[/latex], from sulfur dioxide, [latex]\ce{SO2}[/latex], and oxygen, [latex]\ce{O2}[/latex], shown here. At high temperatures, the rate of formation of [latex]\ce{SO3}[/latex] is higher, but the equilibrium amount (concentration or partial pressure) of [latex]\ce{SO3}[/latex] is lower than it would be at lower temperatures.  [latex]\ce{2SO2}(g) + \ce{O2}(g) \longrightarrow \ce{2SO3}(g)[/latex]
    1. Does the equilibrium constant for the reaction increase, decrease, or remain about the same as the temperature increases?
    2. Is the reaction endothermic or exothermic?
  5. Explain how to recognize the conditions under which changes in pressure would affect systems at equilibrium.
  6. Suggest four ways in which the concentration of PH3 could be increased in an equilibrium described by the following equation: [latex]{\text{P}}_{4}\left(g\right)+6{\text{H}}_{2}\left(g\right)\rightleftharpoons4{\text{PH}}_{3}\left(g\right)\Delta H=110.5\text{kJ}[/latex]
  7. What would happen to the color of the solution in part (b) of Figure 1 if a small amount of [latex]\ce{NaOH}[/latex] were added and[latex]\ce{ Fe(OH)}[/latex]3 precipitated? Explain your answer.
  8. How will an increase in temperature affect each of the following equilibria? How will a decrease in the volume of the reaction vessel affect each?
    1. [latex]2{\text{H}}_{2}\text{O}\left(g\right)\rightleftharpoons2{\text{H}}_{2}\left(g\right)+{\text{O}}_{2}\left(g\right)\Delta H=484\text{kJ}[/latex]
    2. [latex]{\text{N}}_{2}\left(g\right)+3{\text{H}}_{2}\left(g\right)\rightleftharpoons2{\text{NH}}_{3}\left(g\right)\Delta H=-92.2\text{kJ}[/latex]
    3. [latex]2\text{Br}\left(g\right)\rightleftharpoons{\text{Br}}_{2}\left(g\right)\Delta H=-224\text{kJ}[/latex]
    4. [latex]{\text{H}}_{2}\left(g\right)+{\text{I}}_{2}\left(s\right)\rightleftharpoons2\text{HI}\left(g\right)\Delta H=53\text{kJ}[/latex]
  9. Suggest four ways in which the concentration of hydrazine, [latex]\ce{N2H4}[/latex], could be increased in an equilibrium described by the following equation: [latex]{\text{N}}_{2}\left(g\right)+2{\text{H}}_{2}\left(g\right)\rightleftharpoons{\text{N}}_{2}{\text{H}}_{4}\left(g\right)\Delta H=95\text{kJ}[/latex]
  10. Pure iron metal can be produced by the reduction of iron(III) oxide with hydrogen gas.
    1. Write the expression for the equilibrium constant (Kc) for the reversible reaction
      [latex]{\text{Fe}}_{2}{\text{O}}_{3}\left(s\right)+3{\text{H}}_{2}\left(g\right)\rightleftharpoons2\text{Fe}\left(s\right)+3{\text{H}}_{2}\text{O}\left(g\right)\Delta H=98.7\text{kJ}[/latex]
    2. What will happen to the concentration of each reactant and product at equilibrium if more Fe is added?
    3. What will happen to the concentration of each reactant and product at equilibrium if H2O is removed?
    4. What will happen to the concentration of each reactant and product at equilibrium if H2 is added?
    5. What will happen to the concentration of each reactant and product at equilibrium if the pressure on the system is increased by reducing the volume of the reaction vessel?
    6. What will happen to the concentration of each reactant and product at equilibrium if the temperature of the system is increased?
  11. How will an increase in temperature affect each of the following equilibria? How will a decrease in the volume of the reaction vessel affect each?
    1. [latex]2{\text{NH}}_{3}\left(g\right)\rightleftharpoons{\text{N}}_{2}\left(g\right)+3{\text{H}}_{2}\left(g\right)\Delta H=92\text{kJ}[/latex]
    2. [latex]{\text{N}}_{2}\left(g\right)+{\text{O}}_{2}\left(g\right)\rightleftharpoons2\text{NO}\left(g\right)\Delta H=181\text{kJ}[/latex]
    3. [latex]2{\text{O}}_{3}\left(g\right)\rightleftharpoons3{\text{O}}_{2}\left(g\right)\Delta H=-285\text{kJ}[/latex]
    4. [latex]\text{CaO}\left(s\right)+{\text{CO}}_{2}\left(g\right)\rightleftharpoons{\text{CaCO}}_{3}\left(s\right)\Delta H=-176\text{kJ}[/latex]
  12. Acetic acid is a weak acid that reacts with water according to this equation: [latex]{\text{CH}}_{3}{\text{CO}}_{2}\text{H}\left(aq\right)+{\text{H}}_{2}\text{O}\left(aq\right)\rightleftharpoons{\text{H}}_{3}{\text{O}}^{+}\left(aq\right)+{\text{CH}}_{3}{\text{CO}}_{2}{}^{-}\left(aq\right)[/latex]
    Will any of the following increase the percent of acetic acid that reacts and produces [latex]{\text{CH}}_{3}{\text{CO}}_{2}{}^{-}[/latex] ion?

    1. Addition of [latex]\ce{HCl}[/latex]
    2. Addition of [latex]\ce{NaOH}[/latex]
    3. Addition of [latex]\ce{NaCH3CO2}[/latex]
  13. Methanol, a liquid fuel that could possibly replace gasoline, can be prepared from water gas and hydrogen at high temperature and pressure in the presence of a suitable catalyst.
    1. Write the expression for the equilibrium constant (Kc) for the reversible reaction
      [latex]2{\text{H}}_{2}\left(g\right)+\text{CO}\left(g\right)\rightleftharpoons{\text{CH}}_{3}\text{OH}\left(g\right)\Delta H=-90.2\text{kJ}[/latex]
    2. What will happen to the concentrations of [latex]\ce{H2, CO}[/latex], and [latex]\ce{CH3OH}[/latex] at equilibrium if more [latex]\ce{H2}[/latex] is added?
    3. What will happen to the concentrations of [latex]\ce{H2}, \ce{CO}[/latex], and [latex]\ce{CH3OH}[/latex] at equilibrium if [latex]\ce{CO}[/latex] is removed?
    4. What will happen to the concentrations of [latex]\ce{H2, CO}[/latex], and [latex]\ce{CH3OH}[/latex] at equilibrium if [latex]\ce{CH3OH}[/latex] is added?
    5. What will happen to the concentrations of [latex]\ce{H2, CO}[/latex], and [latex]\ce{CH3OH}[/latex] at equilibrium if the temperature of the system is increased?
    6. What will happen to the concentrations of [latex]\ce{H2, CO}[/latex], and [latex]\ce{CH3OH}[/latex] at equilibrium if more catalyst is added?
  14. How can the pressure of water vapor be increased in the following equilibrium? [latex]{\text{H}}_{2}\text{O}\left(l\right)\rightleftharpoons{\text{H}}_{2}\text{O}\left(g\right)\Delta H=41\text{kJ}[/latex]
  15. Water gas, a mixture of [latex]\ce{H2}[/latex] and [latex]\ce{CO}[/latex], is an important industrial fuel produced by the reaction of steam with red hot coke, essentially pure carbon.
    1. Write the expression for the equilibrium constant for the reversible reaction
      [latex]\text{C}\left(s\right)+{\text{H}}_{2}\text{O}\left(g\right)\rightleftharpoons\text{CO}\left(g\right)+{\text{H}}_{2}\left(g\right)\Delta H=131.30\text{kJ}[/latex]
    2. What will happen to the concentration of each reactant and product at equilibrium if more [latex]\ce{C}[/latex] is added?
    3. What will happen to the concentration of each reactant and product at equilibrium if [latex]\ce{H2O}[/latex] is removed?
    4. What will happen to the concentration of each reactant and product at equilibrium if [latex]\ce{CO}[/latex] is added?
    5. What will happen to the concentration of each reactant and product at equilibrium if the temperature of the system is increased?
  16. Ammonia is a weak base that reacts with water according to this equation: [latex]{\text{NH}}_{3}\left(aq\right)+{\text{H}}_{2}\text{O}\left(l\right)\rightleftharpoons{\text{NH}}_{4}{}^{+}\left(aq\right)+{\text{OH}}^{-}\left(aq\right)[/latex]
    Will any of the following increase the percent of ammonia that is converted to the ammonium ion in water?

    1. Addition of [latex]\ce{NaOH}[/latex]
    2. Addition of [latex]\ce{HCl}[/latex]
    3. Addition of [latex]\ce{NH4Cl}[/latex]
  17. Suggest two ways in which the equilibrium concentration of [latex]\ce{Ag+}[/latex] can be reduced in a solution of [latex]\ce{Na+, Cl-, Ag+}[/latex], and [latex]{\text{NO}}_{3}{}^{\text{-}}[/latex], in contact with solid [latex]\ce{AgCl}[/latex]. [latex]{\text{Na}}^{+}\left(aq\right)+{\text{Cl}}^{-}\left(aq\right)+{\text{Ag}}^{+}\left(aq\right)+{\text{NO}}_{3}{}^{-}\left(aq\right)\rightleftharpoons\text{AgCl}\left(s\right)+{\text{Na}}^{+}\left(aq\right)+{\text{NO}}_{3}{}^{-}\left(aq\right)[/latex]
    [latex]\Delta H=-65.9\text{kJ}[/latex]
  18. [latex]\ce{BaSO4}[/latex], an insoluble solid, is added to a solution of barium ion and sulfate ion at equilibrium with solid barium sulfate. [latex]\ce{Ba2+}(aq) + \ce{SO42-}(aq) \longrightarrow \ce{BaSO4}(s)[/latex] Which of the following will occur?
    1. [latex]\ce{Ba2+}[/latex] and [latex]\ce{SO42-}[/latex] concentrations will remain unchanged
    2. The added barium sulfate will dissolve.
    3. Additional barium sulfate will precipitate from solution
    4. The [latex]\ce{Ba2+}[/latex] and [latex]\ce{SO42-}[/latex] concentrations will increase
Show Selected Solutions
  1. The change in enthalpy may be used. If the reaction is exothermic, the heat produced can be thought of as a product. If the reaction is endothermic the heat added can be thought of as a reactant. Additional heat would shift an exothermic reaction back to the reactants but would shift an endothermic reaction to the products. Cooling an exothermic reaction causes the reaction to shift toward the product side; cooling an endothermic reaction would cause it to shift to the reactants’ side.
  2. The answers are as follows:
    1. For the yield to decrease from that obtained at a lower temperature, the value of K must decrease with an increase in temperature.
    2. The observation that K decreases with an increase in temperature indicates the reaction is exothermic.
  3. Add [latex]\ce{P4}[/latex]; add [latex]\ce{H2}[/latex]; decrease the container volume; heat the mixture.
  4. The answers are as follows:
    1. T increase = shift right, V decrease = shift left;
    2. T increase = shift left, V decrease = shift right; T increase = shift left, V decrease = shift right;
    3. T increase = shift right, V decrease = shift left.
  5. The answers are as follows:
    1. Kc = [latex]\frac{[\ce{H2O}]^3}{[\ce{H}]^3}[/latex]
    2. no changes occur;
    3. [latex]\ce{H2}[/latex] decreases, [latex]\ce{H2O}[/latex] decreases;
    4. [latex]\ce{H2}[/latex] increases, [latex]\ce{H2O}[/latex] increases;
    5. [latex]\ce{H2}[/latex] increases, [latex]\ce{H2O}[/latex] increases (concentrations rise due to decreased volume, but there is no shift in the equilibrium);
    6. [latex]\ce{H2}[/latex] decreases, [latex]\ce{H2O}[/latex] increases. In (b), (c), (d), (e), and (f), the mass of [latex]\ce{Fe}[/latex] will change, but its concentration (activity) will not change.
  6. Only (b). In (a), the addition of [latex]\ce{HCl}[/latex] increase the [latex]\ce{H3O+}[/latex] concentration and shifts the equilibrium to the left, decreasing the acetate ion concentration and increasing the acetic acid concentration. In (b), the addition of a strong base consumes [latex]\ce{H3O+}[/latex] and shifts the equilibrium to the right, forming acetate ion. In (c), addition of the acetate ion shifts the equilibrium left, increasing the concentration of acetic acid.
  7. Add heat or reduce the pressure.
  8. b. addition of [latex]\ce{HCl}[/latex] will remove [latex]\ce{OH-}[/latex] from the mixture. This removes product and will shift equilibrium to the right.
  9. d


14.4 Equilibrium Calculations [Go to section 14.4]

  1. Acetic acid, [latex]\ce{HC2H3O2}[/latex], is in equilibrium with its ions: [latex]\ce{HC2H3O2}(aq)[/latex] [latex]\leftrightarrow[/latex] [latex]\ce{H+}(aq) +  \ce{C2H3O2-}(aq)[/latex] Keq = 1.8 × 10-5. At equilibrium, the concentration of the ions are: [latex]\ce{[H+]}[/latex] = 1.33 × 10-3 M. [latex]\ce{[C2H3O2^-]}[/latex] = 1.33 × 10-3 M. Calculate the concentration of the acid, [latex]\ce{HC2H3O2}[/latex].
  2. When heated, iodine vapor dissociates according to this equation: [latex]{\text{I}}_{2}\left(g\right)\rightleftharpoons2\text{I}\left(g\right)[/latex]
    At 1274 K, a sample exhibits a partial pressure of [latex]\ce{I2}[/latex] of 0.1122 atm and a partial pressure due to [latex]\ce{I}[/latex] atoms of 0.1378 atm. Determine the value of the equilibrium constant, KP, for the decomposition at 1274 K.
  3. [latex]\ce{CaCO3}[/latex] (chalk) can produce solid [latex]\ce{CaO}[/latex] and [latex]\ce{CO2}[/latex] gas when heated. If 6.0 moles of carbon dioxide forms in a 4.500 L reaction vessel, what is the equilibrium constant for this reaction?
  4. At a temperature of 60 °C, the vapor pressure of water is 0.196 atm. What is the value of the equilibrium constant KP for the transformation at 60 °C? [latex]{\text{H}}_{2}\text{O}\left(l\right)\rightleftharpoons{\text{H}}_{2}\text{O}\left(g\right)[/latex]
  5. Le Chatelier’s Principle states that if a stress is applied to a reversible reaction at equilibrium, the reaction will undergo a shift in order to re-establish its equilibrium. Consider the following exothermic reversible reaction at equilibrium:
    2 A ↔ B + C. Give an example of a change that would shift this reaction to the right. Give an example of a change that would shift this reaction to the left.
  6. Carbon reacts with water vapor at elevated temperatures.
    [latex]\text{C}\left(s\right)+{\text{H}}_{2}\text{O}\left(g\right)\rightleftharpoons\text{CO}\left(g\right)+{\text{H}}_{2}\left(g\right){K}_{c}=0.2\text{ at }1000^{\circ}\text{C}[/latex]
    What is the concentration of [latex]\ce{CO}[/latex] in an equilibrium mixture with [latex]\ce{H2O}[/latex] = 0.500 M at 1000 °C?
  7. For the following reaction at equilibrium at 2000°C, the concentration of [latex]\ce{N2}[/latex] and [latex]\ce{O2}[/latex] are both 4.8 M. [latex]\ce{N2}(g) + \ce{O2}(g) \leftrightarrow 2 \ce{NO}(g)[/latex] Keq = 6.3 x 10-4. Calculate the concentration of [latex]\ce{NO}[/latex] at equilibrium. Show your work; pay careful attention to exponents.
  8. A student solved the following problem and found [latex]\ce{N2O4}[/latex] = 0.16 M at equilibrium. How could this student recognize that the answer was wrong without reworking the problem? The problem was: What is the equilibrium concentration of [latex]\ce{N2O4}[/latex] in a mixture formed from a sample of [latex]\ce{NO2}[/latex] with a concentration of 0.10 M?
    [latex]2{\text{NO}}_{2}\left(g\right)\rightleftharpoons{\text{N}}_{2}{\text{O}}_{4}\left(g\right){K}_{c}=160[/latex]
  9. A reaction is represented by this equation: [latex]\text{A}\left(aq\right)+2\text{B}\left(aq\right)\rightleftharpoons2\text{C}\left(aq\right){K}_{c}=1\times {10}^{3}[/latex]
    1. Write the mathematical expression for the equilibrium constant.
    2. Using concentrations ≤ 1 M, make up two sets of concentrations that describe a mixture of A, B, and C at equilibrium.
  10. Why would we not include [latex]\ce{C}[/latex] in the equilibrium expression for the following reaction? [latex]\ce{2CO}(g) \leftrightarrow \ce{CO2}(g) + \ce{C}(s)[/latex]
  11. A reaction is represented by this equation: [latex]2\text{W}\left(aq\right)\rightleftharpoons\text{X}\left(aq\right)+2\text{Y}\left(aq\right){K}_{c}=5\times {10}^{-4}[/latex]
    1. Write the mathematical expression for the equilibrium constant.
    2. Using concentrations of ≤ 1 M, make up two sets of concentrations that describe a mixture of W, X, and Y at equilibrium.
  12. Assume that the change in concentration of [latex]\ce{COCl2}[/latex] is small enough to be neglected in the following problem. Calculate the equilibrium concentration of all species in an equilibrium mixture that results from the decomposition of [latex]\ce{COCl2}[/latex] with an initial concentration of 0.3166 M. [latex]{\text{COCl}}_{2}\left(g\right)\rightleftharpoons\text{CO}\left(g\right)+{\text{Cl}}_{2}\left(g\right){K}_{c}=2.2\times {10}^{-10}[/latex]. Show that the change is small enough to be neglected.
  13. What is the value of the equilibrium constant at 500 °C for the formation of [latex]\ce{NH3}[/latex] according to the following equation? [latex]{\text{N}}_{2}\left(g\right)+3{\text{H}}_{2}\left(g\right)\rightleftharpoons2{\text{NH}}_{3}\left(g\right)[/latex]
    An equilibrium mixture of [latex]\ce{NH3}(g), \ce{H2}(g), \text{ and } \ce{N2}(g)[/latex] at 500 °C was found to contain 1.35 M [latex]\ce{H2}[/latex], 1.15 M [latex]\ce{N2}[/latex], and 4.12 × 10-1 M [latex]\ce{NH3}[/latex].
  14. What are all concentrations after a mixture that contains [latex]\ce{[H2O]}[/latex] = 1.00 M and [latex]\ce{[Cl2O]}[/latex] = 1.00 M comes to equilibrium at 25 °C?
    [latex]{\text{H}}_{2}\text{O}\left(g\right)+{\text{Cl}}_{2}\text{O}\left(g\right)\rightleftharpoons2\text{HOCl}\left(g\right){K}_{c}=0.0900[/latex]
  15. A 0.72-mol sample of [latex]\ce{PCl5}[/latex] is put into a 1.00-L vessel and heated. At equilibrium, the vessel contains 0.40 mol of [latex]\ce{PCl3}(g)[/latex] and 0.40 mol of [latex]\ce{Cl2}(g)[/latex]. Calculate the value of the equilibrium constant for the decomposition of [latex]\ce{PCl5} \text{ to } \ce{PCl3} \text{ and } \ce{Cl2}[/latex] at this temperature.
  16. Calculate the number of moles of [latex]\ce{HI}[/latex] that are at equilibrium with 1.25 mol of [latex]\ce{H2}[/latex] and 1.25 mol of [latex]\ce{I2}[/latex] in a 5.00-L flask at 448 °C.
    [latex]{\text{H}}_{2}+{\text{I}}_{2}\rightleftharpoons2\text{HI}{K}_{c}=50.2\text{ at }448^{\circ}\text{C}[/latex]
  17. Calculate the value of the equilibrium constant KP for the reaction [latex]2\text{NO}\left(g\right)+{\text{Cl}}_{2}\left(g\right)\rightleftharpoons2\text{NOCl}\left(g\right)[/latex] from these equilibrium pressures: [latex]\ce{NO}[/latex], 0.050 atm; [latex]\ce{Cl2}[/latex], 0.30 atm; [latex]\ce{NOCl}[/latex], 1.2 atm.
  18. What is the pressure of [latex]\ce{CO2}[/latex] in a mixture at equilibrium that contains 0.50 atm [latex]\ce{H2}[/latex], 2.0 atm of [latex]\ce{H2O}[/latex], and 1.0 atm of [latex]\ce{CO}[/latex] at 990 °C? [latex]{\text{H}}_{2}\left(g\right)+{\text{CO}}_{2}\left(g\right)\rightleftharpoons{\text{H}}_{2}\text{O}\left(g\right)+\text{CO}\left(g\right){K}_{P}=1.6\text{ at }990^{\circ}\text{C}[/latex]
  19. A sample of ammonium chloride was heated in a closed container: [latex]{\text{NH}}_{4}\text{Cl}\left(s\right)\rightleftharpoons{\text{NH}}_{3}\left(g\right)+\text{HCl}\left(g\right)[/latex]
    At equilibrium, the pressure of [latex]\ce{NH3}[/latex](g) was found to be 1.75 atm. What is the value of the equilibrium constant KP for the decomposition at this temperature?
  20. Calcium chloride 6-hydrate, [latex]\ce{CaCl2}[/latex] [latex]\cdot[/latex] [latex]\ce{6H2O}[/latex], dehydrates according to the equation
    [latex]{\text{CaCl}}_{2}\cdot 6{\text{H}}_{2}\text{O}\left(s\right)\rightleftharpoons{\text{CaCl}}_{2}\left(s\right)+6{\text{H}}_{2}\text{O}\left(g\right){K}_{P}=5.09\times {10}^{-44}\text{ at }25^{\circ}\text{C}[/latex]
    What is the pressure of water vapor at equilibrium with a mixture of [latex]\ce{CaCl2}[/latex] [latex]\cdot[/latex] [latex]\ce{6H2O} \text{ and } \ce{CaCl2}[/latex]?
  21. Cobalt metal can be prepared by reducing cobalt(II) oxide with carbon monoxide.
    [latex]\text{CoO}\left(s\right)+\text{CO}\left(g\right)\rightleftharpoons\text{Co}\left(s\right)+{\text{CO}}_{2}\left(g\right){K}_{c}=4.90\times {10}^{2}\text{ at }550^{\circ}\text{C}[/latex]
    What concentration of [latex]\ce{CO}[/latex] remains in an equilibrium mixture with [latex]\ce{[CO2]}[/latex] = 0.100 M?
  22. Butane exists as two isomers, n-butane and isobutane.
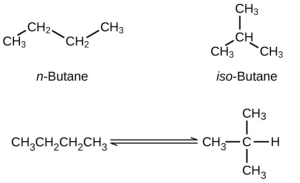
    KP = 2.5 at 25 °C What is the pressure of isobutane in a container of the two isomers at equilibrium with a total pressure of 1.22 atm?
  23.  A student solved the following problem and found the equilibrium concentrations to be [latex]\ce{[SO2]}[/latex] = 0.590 M, [latex]\ce{[O2]}[/latex] = 0.0450 M, and [latex]\ce{[SO3]}[/latex] = 0.260 M. How could this student check the work without reworking the problem? The problem was: For the following reaction at 600 °C: [latex]2{\text{SO}}_{2}\left(g\right)+{\text{O}}_{2}\left(g\right)\rightleftharpoons2{\text{SO}}_{3}\left(g\right){K}_{c}=4.32[/latex] What are the equilibrium concentrations of all species in a mixture that was prepared with [latex]\ce{[SO3]}[/latex] = 0.500 M, [latex]\ce{[SO2]}[/latex] = 0 M, and [latex]\ce{[O2]}[/latex] = 0.350 M
  24. The equilibrium constant (Kc) for this reaction is 5.0 at a given temperature: [latex]\text{CO}\left(g\right)+{\text{H}}_{2}\text{O}\left(g\right)\rightleftharpoons{\text{CO}}_{2}\left(g\right)+{\text{H}}_{2}\left(g\right)[/latex]
    1. On analysis, an equilibrium mixture of the substances present at the given temperature was found to contain 0.20 mol of [latex]\ce{CO}[/latex], 0.30 mol of water vapor, and 0.90 mol of [latex]\ce{H2}[/latex] in a liter. How many moles of [latex]\ce{CO2}[/latex] were there in the equilibrium mixture?
    2. Maintaining the same temperature, additional [latex]\ce{H2}[/latex] was added to the system, and some water vapor was removed by drying. A new equilibrium mixture was thereby established containing 0.40 mol of [latex]\ce{CO}[/latex], 0.30 mol of water vapor, and 1.2 mol of [latex]\ce{H2}[/latex] in a liter. How many moles of [latex]\ce{CO2}[/latex] were in the new equilibrium mixture? Compare this with the quantity in part (a), and discuss whether the second value is reasonable. Explain how it is possible for the water vapor concentration to be the same in the two equilibrium solutions even though some vapor was removed before the second equilibrium was established.
  25. Complete the changes in concentrations (or pressure, if requested) for each of the following reactions.
    1. [latex]\begin{array}{llll}2{\text{SO}}_{3}\left(g\right)\hfill & \rightleftharpoons\hfill & 2{\text{SO}}_{2}\left(g\right)+\hfill & {\text{O}}_{2}\left(g\right)\hfill \\ \text{ }\hfill & & \text{ }\hfill & +x\hfill \\ \text{ }\hfill & & \text{ }\hfill & 0.125M\hfill \end{array}[/latex]
    2. [latex]\begin{array}{lllll}4{\text{NH}}_{3}\left(g\right)\hfill & +3{\text{O}}_{2}\left(g\right)\hfill & \rightleftharpoons\hfill & 2{\text{N}}_{2}\left(g\right)+\hfill & 6{\text{H}}_{2}\text{O}\left(g\right)\hfill \\ \text{ }\hfill & 3x\hfill & & \text{ }\hfill & \text{ }\hfill \\ \text{ }\hfill & 0.24M\hfill & & \text{ }\hfill & \text{ }\hfill \end{array}[/latex]
    3. Change in pressure:
      [latex]\begin{array}{llll}2{\text{CH}}_{4}\left(g\right)\hfill & \rightleftharpoons\hfill & {\text{C}}_{2}{\text{H}}_{2}\left(g\right)+\hfill & 3{\text{H}}_{2}\left(g\right)\hfill \\ \text{ }\hfill & & x\hfill & \text{ }\hfill \\ \text{ }\hfill & & 25\text{torr}\hfill & \text{ }\hfill \end{array}[/latex]
    4. Change in pressure:
      [latex]\begin{array}{lllll}{\text{CH}}_{4}\left(g\right)+\hfill & {\text{H}}_{2}\text{O}\left(g\right)\hfill & \rightleftharpoons\hfill & \text{CO}\left(g\right)+\hfill & 3{\text{H}}_{2}\left(g\right)\hfill \\ \text{ }\hfill & x\hfill & & \text{ }\hfill & \text{ }\hfill \\ \text{ }\hfill & 5\text{atm}\hfill & & \text{ }\hfill & \text{ }\hfill \end{array}[/latex]
    5. [latex]\begin{array}{llll}{\text{NH}}_{4}\text{Cl}\left(s\right)\hfill & \rightleftharpoons\hfill & {\text{NH}}_{3}\left(g\right)+\hfill & \text{HCl}\left(g\right)\hfill \\ & & x\hfill & \text{ }\hfill \\ & & \hfill 1.03\times {10}^{-4}M\hfill & \text{ }\hfill \end{array}[/latex]
    6. change in pressure:
      [latex]\begin{array}{cccc}\text{Ni}\left(s\right)+\hfill & 4\text{CO}\left(g\right)\hfill & \rightleftharpoons\hfill & \text{Ni}{\left(\text{CO}\right)}_{4}\left(g\right)\hfill \\ & 4x\hfill & & \text{ }\hfill \\ & \hfill 0.40\text{atm}\hfill & & \text{ }\hfill \end{array}[/latex]
  26. Consider the equilibrium: [latex]4{\text{NO}}_{2}\left(g\right)+6{\text{H}}_{2}\text{O}\left(g\right)\rightleftharpoons4{\text{NH}}_{3}\left(g\right)+7{\text{O}}_{2}\left(g\right)[/latex]
    1. What is the expression for the equilibrium constant (Kc) of the reaction?
    2. How must the concentration of [latex]\ce{NH3}[/latex] change to reach equilibrium if the reaction quotient is less than the equilibrium constant?
    3. If the reaction were at equilibrium, how would a decrease in pressure (from an increase in the volume of the reaction vessel) affect the pressure of [latex]\ce{NO2}[/latex]?
    4. If the change in the pressure of [latex]\ce{NO2}[/latex] is 28 torr as a mixture of the four gases reaches equilibrium, how much will the pressure of [latex]\ce{O2}[/latex] change?
  27. Complete the changes in concentrations (or pressure, if requested) for each of the following reactions.
    1. [latex]\begin{array}{cccc}2{\text{H}}_{2}\left(g\right)+\hfill & {\text{O}}_{2}\left(g\right)\hfill & \rightleftharpoons\hfill & 2{\text{H}}_{2}\text{O}\left(g\right)\hfill \\ \text{ }\hfill & \text{ }\hfill & & +2x\hfill \\ \text{ }\hfill & \text{ }\hfill & & 1.50M\hfill \end{array}[/latex]
    2. [latex]\begin{array}{ccccc}{\text{CS}}_{2}\left(g\right)+\hfill & 4{\text{H}}_{2}\left(g\right)\hfill & \rightleftharpoons\hfill & {\text{CH}}_{4}\left(g\right)+\hfill & 2{\text{H}}_{2}\text{S}\left(g\right)\hfill \\ x\hfill & \text{ }\hfill & & \text{ }\hfill & \text{ }\hfill \\ 0.020M\hfill & \text{ }\hfill & & \text{ }\hfill & \text{ }\hfill \end{array}[/latex]
    3. Change in pressure:
      [latex]\begin{array}{cccc}{\text{H}}_{2}\left(g\right)+\hfill & {\text{Cl}}_{2}\left(g\right)\hfill & \rightleftharpoons\hfill & 2\text{HCl}\left(g\right)\hfill \\ x\hfill & \text{ }\hfill & & \text{ }\hfill \\ 1.50\text{atm}\hfill & \text{ }\hfill & & \text{ }\hfill \end{array}[/latex]
    4. Change in pressure:
      [latex]\begin{array}{ccccc}2{\text{NH}}_{3}\left(g\right)\hfill & +2{\text{O}}_{2}\left(g\right)\hfill & \rightleftharpoons\hfill & {\text{N}}_{2}\text{O}\left(g\right)+\hfill & 3{\text{H}}_{2}\text{O}\left(g\right)\hfill \\ \text{ }\hfill & \text{ }\hfill & & \text{ }\hfill & x\hfill \\ \text{ }\hfill & \text{ }\hfill & & \text{ }\hfill & 60.6\text{torr}\hfill \end{array}[/latex]
    5. [latex]\begin{array}{cccc}{\text{NH}}_{4}\text{HS}\left(s\right)\hfill & \rightleftharpoons\hfill & {\text{NH}}_{3}\left(g\right)+\hfill & {\text{H}}_{2}\text{S}\left(g\right)\hfill \\ & & x\hfill & \text{ }\hfill \\ & & 9.8\times {10}^{-6}M\hfill & \text{ }\hfill \end{array}[/latex]
    6. Change in pressure:
      [latex]\begin{array}{cccc}\text{Fe}\left(s\right)+\hfill & 5\text{CO}\left(g\right)\hfill & \rightleftharpoons\hfill & \text{Fe}{\left(\text{CO}\right)}_{4}\left(g\right)\hfill \\ & \text{ }\hfill & & x\hfill \\ & \text{ }\hfill & & 0.012\text{atm}\hfill \end{array}[/latex]
  28. Liquid [latex]\ce{N2O3}[/latex] is dark blue at low temperatures, but the color fades and becomes greenish at higher temperatures as the compound decomposes to [latex]\ce{NO}[/latex] and [latex]\ce{NO2}[/latex]. At 25 °C, a value of KP = 1.91 has been established for this decomposition. If 0.236 moles of [latex]\ce{N2O3}[/latex] are placed in a 1.52-L vessel at 25 °C, calculate the equilibrium partial pressures of [latex]\ce{N2O3}(g), \ce{NO2}(g), \text{ and } \ce{NO}(g)[/latex].
  29. Why would [latex]\ce{Ni}[/latex] not be included in the equilibrium equation for [latex]\ce{NIO}(s) + \ce{CO}(g) \leftrightarrow \ce{Ni}(s) + \ce{CO2}(g)[/latex] ? What property of [latex]\ce{Ni}[/latex] does change?
  30. Assume that the change in pressure of [latex]\ce{H2S}[/latex] is small enough to be neglected in the following problem. Calculate the equilibrium pressures of all species in an equilibrium mixture that results from the decomposition of [latex]\ce{H2S}[/latex] with an initial pressure of 0.824 atm.
    [latex]2{\text{H}}_{2}\text{S}\left(g\right)\rightleftharpoons2{\text{H}}_{2}\left(g\right)+{\text{S}}_{2}\left(g\right){K}_{P}=2.2\times {10}^{-6}[/latex]. Show that the change is small enough to be neglected.
  31. What are the concentrations of [latex]\ce{PCl5}, \ce{PCl3}, \text{ and } \ce{Cl2}[/latex] in an equilibrium mixture produced by the decomposition of a sample of pure [latex]\ce{PCl5}[/latex] with [latex]\ce{[PCl5]}[/latex] = 2.00 M?
    [latex]{\text{PCl}}_{5}\left(g\right)\rightleftharpoons{\text{PCl}}_{3}\left(g\right)+{\text{Cl}}_{2}\left(g\right){K}_{c}=0.0211[/latex]
  32. What is the pressure of [latex]\ce{BrCl}[/latex] in an equilibrium mixture of [latex]\ce{Cl2}, \ce{Br2}, \text{ and } \ce{BrCl}[/latex] if the pressure of [latex]\ce{Cl2}[/latex] in the mixture is 0.115 atm and the pressure of [latex]\ce{Br2}[/latex] in the mixture is 0.450 atm?
    [latex]{\text{Cl}}_{2}\left(g\right)+{\text{Br}}_{2}\left(g\right)\rightleftharpoons2\text{BrCl}\left(g\right){K}_{P}=4.7\times {10}^{-2}[/latex]
  33. Sodium sulfate 10-hydrate, [latex]\ce{Na2SO4}[/latex] [latex]\cdot[/latex] [latex]\ce{10H2O}[/latex], dehydrates according to the equation
    [latex]{\text{Na}}_{2}{\text{SO}}_{4}\cdot 10{\text{H}}_{2}\text{O}\left(s\right)\rightleftharpoons{\text{Na}}_{2}{\text{SO}}_{4}\left(s\right)+10{\text{H}}_{2}\text{O}\left(g\right){K}_{P}=4.08\times {10}^{-25}\text{ at }25^{\circ}\text{C}[/latex]
    What is the pressure of water vapor at equilibrium with a mixture of [latex]\ce{Na2SO4}[/latex] [latex]\cdot[/latex] [latex]\ce{10H2O}[/latex] and [latex]\ce{NaSO4}[/latex]?
  34. Calculate the pressures of all species at equilibrium in a mixture of [latex]\ce{NOCl}, \ce{NO}, \text{ and } \ce{Cl2}[/latex] produced when a sample of [latex]\ce{NOCl}[/latex] with a pressure of 0.500 atm comes to equilibrium according to this reaction:
    [latex]2\text{NOCl}\left(g\right)\rightleftharpoons 2\text{NO}\left(g\right)+{\text{Cl}}_{2}\left(g\right){K}_{P}=4.0\times {10}^{-5}[/latex]
  35. One of the important reactions in the formation of smog is represented by the equation
    [latex]{\text{O}}_{3}\left(g\right)+\text{NO}\left(g\right)\rightleftharpoons{\text{NO}}_{2}\left(g\right)+{\text{O}}_{2}\left(g\right){K}_{P}=6.0\times {10}^{34}[/latex]
    What is the pressure of [latex]\ce{O3}[/latex] remaining after a mixture of [latex]\ce{O3}[/latex] with a pressure of 1.2 × 10-8 atm and [latex]\ce{NO}[/latex] with a pressure of 1.2 × 10-8 atm comes to equilibrium? (Hint: KP is large; assume the reaction goes to completion then comes back to equilibrium.)
  36. Consider the following reaction: [latex]\ce{2NOCl}(g) \longrightarrow \ce{2NO}(g) + \ce{Cl2}(g)[/latex] Kp = 3.003 × 10-6. Calculate the pressures of [latex]\ce{NO}, \ce{Cl2}, \text{ and } \ce{NOCl}[/latex] in an equilibrium mixture produced by the reaction of a starting mixture with 4.0 atm [latex]\ce{NO}[/latex] and 2.0 atm [latex]\ce{Cl2}[/latex]. (Hint: KP is small; assume the reverse reaction goes to completion then comes back to equilibrium.)
  37. Calculate the number of grams of HI that are at equilibrium with 1.25 mol of [latex]\ce{H2}[/latex] and 63.5 g of iodine at 448 °C.
    [latex]{\text{H}}_{2}+{\text{I}}_{2}\rightleftharpoons2\text{HI}{K}_{c}=50.2\text{ at }448^{\circ}\text{C}[/latex]
  38. Consider the reaction: [latex]\ce{N2O4}(g) \leftrightarrow \ce{2NO2}(g)[/latex] At 25 °C and at 1 atm, the partial pressures in an equilibrium mixture of [latex]\ce{N2O4}[/latex] and [latex]\ce{NO2}[/latex] are [latex]{\text{P}}_{{\text{N}}_{2}{\text{O}}_{4}}=0.70\text{atm}[/latex] and [latex]{\text{P}}_{{\text{NO}}_{2}}=0.30\text{atm.}[/latex]
    1. Predict how the pressures of [latex]\ce{NO2}[/latex] and [latex]\ce{N2O4}[/latex] will change if the total pressure increases to 9.0 atm. Will they increase, decrease, or remain the same?
    2. Calculate the partial pressures of [latex]\ce{NO2}[/latex] and [latex]\ce{N2O4}[/latex] when they are at equilibrium at 9.0 atm and 25 °C.
  39. In a 3.0-L vessel, the following equilibrium partial pressures are measured: [latex]\ce{N2}[/latex], 190 torr; [latex]\ce{H2}[/latex], 317 torr; [latex]\ce{NH3}[/latex], 1.00 × 103 torr: [latex]{\text{N}}_{2}\left(g\right)+3{\text{H}}_{2}\left(g\right)\rightleftharpoons2{\text{NH}}_{3}\left(g\right)[/latex]
    1. How will the partial pressures of [latex]\ce{H2}, \ce{N2}, \text{ and } \ce{NH3}[/latex] change if [latex]\ce{H2}[/latex] is removed from the system? Will they increase, decrease, or remain the same?
    2. Hydrogen is removed from the vessel until the partial pressure of nitrogen, at equilibrium, is 250 torr. Calculate the partial pressures of the other substances under the new conditions.
  40. Antimony pentachloride decomposes according to this equation: [latex]{\text{SbCl}}_{5}\left(g\right)\rightleftharpoons{\text{SbCl}}_{3}\left(g\right)+{\text{Cl}}_{2}\left(g\right)[/latex]
    An equilibrium mixture in a 5.00-L flask at 448 °C contains 3.85 g of [latex]\ce{SbCl5}[/latex], 9.14 g of [latex]\ce{SbCl3}[/latex], and 2.84 g of [latex]\ce{Cl2}[/latex]. How will the masses of each component change if the volume of the vessel is changed to 2.0L?
  41. Consider the reaction between [latex]\ce{H2}[/latex] and [latex]\ce{O2}[/latex] at 1000 K
    [latex]2H_{2}(g)+O_{2}(g)\rightleftharpoons{2H_{2}O(g)}[/latex] [latex]K_{P}=\frac{(P_{H_{2}O})^{2}}{(P_{O_{2}})(P_{H_{2}})^{3}}=1.33\times{10^{20}}[/latex] If 0.500 atm of [latex]\ce{H2}[/latex] and 0.500 atm of [latex]\ce{O2}[/latex] are allowed to come to equilibrium at this temperature, what are the partial pressures of the components?
Show Selected Solutions
  1. Kp = [latex]\frac{(P_{\ce{I}})^2}{P_{\ce{I2}}}[/latex] = [latex]\frac{(0.1378)^2}{0.1122}[/latex] = 0.1692
  2. In heterogeneous equilibrium systems such as this one, the concentration of the condensed phase is constant at a given temperature. Thus, the equilibrium expression for the transformation [latex]\ce{H2O}(l) \longrightarrow \ce{H2O}(g)[/latex] is written as Kp = P[latex]\ce{H2O}[/latex]. At 60 ºC, the pressure of water vapor at equilibrium with liquid water is 0.196 atm; therefore, the equilibrium constant is KP = 0.196.
  3. From the equilibrium constant expression, Kc = [latex]\frac{[\ce{CO}][\ce{H2}]}{[\ce{H2O}]}[/latex] = [latex]\frac{[\ce{CO}][\ce{H2}]}{0.500}[/latex] = 0.2. Since [latex]\ce{CO}[/latex] must equal [latex]\ce{H2}[/latex], let the concentrations of both [latex]\ce{CO}[/latex] and [latex]\ce{H2}[/latex] be x. x2 = 0.500 × 0.2 = 0.01; x = [CO] = [H2] = 0.3 M.
  4. The stoichiometry of the reaction between [latex]\ce{2NO2}[/latex] and [latex]\ce{N2O4}[/latex] forces the concentration of [latex]\ce{N2O4}[/latex] to be no larger than one-half of that of [latex]\ce{NO2}[/latex]. Therefore, no concentration value for [latex]\ce{N2O4}[/latex] > 0.05 M is possible.
  5. We do not include pure solids in an equilibrium expression because they do not expand to fill the container, the concentration will therefore remain unchanged.
  6. The answers are as follows:
    1. Write the starting conditions, change, and equilibrium conditions in tabular form.
      [latex]\ce{[CO]}[/latex] [latex]\ce{[Cl2]}[/latex] [latex]\ce{[COCl2]}[/latex]
      Initial concentration (M) 0 0 0.3166
      Change (M) +x +x -x
      Equilibrium concentration (M) x x 0.3166 – x

      Since Kc is very small, ignore x in comparison with 0.3166 M. The equilibrium constant expression is
      Kc = [latex]\frac{\ce{[CO]}\ce{[Cl2]}}{\ce{[COCl2]}} = \frac{x^2}{0.3166}[/latex] = 2.2 × 10-10
      x2 = 6.965 × 10-11
      x = 8.3 × 10-6 = [latex]\ce{[CO]} = \ce{[Cl2]}[/latex]
      [latex]\ce{[COCl2]} =[/latex] 0.3166 – 8.3 × 10-6 = 0.3166

    2. The assumption that x is negligibly small compared to 0.3166 is confirmed by comparing the initial concentration of the [latex]\ce{COCl2}[/latex] to its concentration at equilibrium (they are identical when recorded to the proper number of significant digits).
  7. As all species are given in molar concentration, a simple Kc equilibrium can be solved using the balanced equation.
    [latex]\ce{H2O}(g) + \ce{Cl2O}(g) \rightleftharpoons2 \ce{2HOC}(g)[/latex]
    Initial concentration (M) 1.00 1.00 0
    Change (M) -x -x +2x
    Equilibrium concentration (M) 1.00 – x 1.00 – x 2x

    Kc = [latex]\frac{[2x]^2}{[1.00 - x][1.00 - x]} = \frac{[2x]^2}{[1.00 - x]^2}[/latex] = 0.0900
    Since the top and bottom are squared then take the square root of both sides.

    0.3 = [latex]\frac{[2x]}{[1.00 - x]}[/latex], 0.3 – 0.3x = 2x, 0.3 = 2.3x, x = 0.130 M
    Final equilibrium concentrations:

    [latex]\ce{[H2O]} = \ce{[Cl2O]}[/latex] = 1.00 – x = 1.00 – 0.130 = 0.870 M

    [latex]\ce{[HOCl]}[/latex] = 2x = 2(0.130 M) = 0.260 M

  8. Write the equilibrium constant expression, and then solve for [latex]\ce{[HI]}[/latex]. From [latex]\ce{[HI]}[/latex], determine the moles of [latex]\ce{HI}[/latex] present.
    Kc = [latex]\frac{\ce{[HI]^2}}{\ce{[H2]}\ce{[I2]}} = \frac{\ce{[HI]^2}}{[\frac{1.25}{5.00}] [\frac{1.25}{5.00}]}[/latex] = 50.2
    [latex]\ce{[HI]^2}[/latex] = (0.250)2 × 50.2 = 3.14
    [latex]\ce{[HI]}[/latex] = 1.77 M
    5 L × 1.77 M = 8.85 mol [latex]\ce{HI}[/latex]
  9. Write the equilibrium constant expression and solve for P[latex]\ce{CO2}[/latex]
    KP = [latex]\frac{P_{\ce{H2O}}P_{\ce{CO}}}{P_{\ce{H2}}P_{\ce{CO2}}} = \frac{(2.0)(1.0)}{(0.50)P_{\ce{CO2}}}[/latex] = 1.6
    P[latex]\ce{CO2}[/latex] = [latex]\frac{2.0 × 1.0}{0.5 × 1.6}[/latex] = 2.5 atm
  10. Two of the components of this system are solids and have activities of 1. Their pressures are constant and do not enter into the equilibrium expression.
    KP = (P[latex]\ce{H2O}[/latex])6 = 5.09 × 10-44
    P[latex]\ce{H2O}[/latex] = [latex]\sqrt [6]{5.09 × 10^{-44}}[/latex] = 6.09 × 10-8atm
  11. KP = [latex]\frac{P_{\text{isobutane}}}{P_{n-\text{butane}}}[/latex] = 2.5
    Let x be the partial pressure of n-butane.
    [latex]\frac{1.22 \text{ atm } - x}{x}[/latex] = 2.5
    2.5x + x = 1.22
    3.5x = 1.22
    x = 0.35 atm = Pn-butane
    Pisobutane = 1.22 – x = 0.87 atm
  12. The answers are as follows:
    1. For this reaction, Kc = [latex]\frac{\ce{[CO2]}\ce{[H2]}}{\ce{[CO]}\ce{[H2O]}}[/latex] = 5.0. The concentrations at equilibrium are 0.20 M [latex]\ce{CO}[/latex], 0.30 M [latex]\ce{H2O}[/latex], and 0.90 M [latex]\ce{H2}[/latex]. Substitution gives K = 5.0 = [latex]\frac{\ce{[CO2]}[0.90]}{[0.20][0.30]}[/latex]; [latex]\ce{[CO2]}[/latex] = [latex]\frac{5.0(0.20)(0.30)}{0.90}[/latex] = 0.33 M ; Amount of [latex]\ce{CO2}[/latex] = 0.33 mol  × 1 = 0.33 mol
    2. At the particular temperature of reaction, Kc remains constant at 5.0. The new concentrations are 0.40 M [latex]\ce{CO}[/latex], 0.30 M [latex]\ce{H2O}[/latex], and 1.2 M [latex]\ce{H2}[/latex]. [latex]\frac{}{}[/latex] = 0.50, [latex]\ce{[CO2]}[/latex] = 0.50 M. Amount of [latex]\ce{CO2}[/latex] = 0.50 mol × 1 = 0.50 mol. Added [latex]\ce{H2}[/latex] forms some water as a result of a shift to the left after [latex]\ce{H2}[/latex] is added.
  13. The answers are as follows:
    1. Kc = [latex]\frac{\ce{[NH3]^4}\ce{[O2]^7}}{\ce{[NO2]^4}\ce{H2O}^6}[/latex]
    2. Because [latex]\ce{[NH3]}[/latex] is in the numerator of Kc, [latex]\ce{[NH3]}[/latex] must increase for Qc to reach Kc.
    3. The increase in system volume would lower the partial pressures of all reactants (including [latex]\ce{NO2}[/latex]).
    4. The relative changes in pressures are related by the stoichiometry of the reaction. P[latex]\ce{O2}[/latex] = [latex]\frac{7}{4}P_{\ce{NO2}} = \frac{7}{4}[/latex](28 torr) = 49 torr
  14. Write the balanced equilibrium expression. With all of the species as gases, it is a straightforward KP problem to solve. However, all species must be converted to pressures, from other units related to concentration. For [latex]\ce{N2O3}[/latex], with 0.236 mol in 1.52 L at 25 ºC:
    PV = nRT
    [latex]\begin{array}{lll} P  & = & \frac{n}{V}RT \\ & = & \frac{0.236 \cancel{\text{ mol}}}{1.52 \cancel{\text{ L}}} × \frac{(0.08206 \cancel{\text{ L}} \text{ atm})(298.15 \cancel{\text{K}})}{\cancel{\text{mol  K}}} \\ & = & 3.80 \text{ atm} \\ \end{array}[/latex]
    Write the balanced equation and the equilibrium changes:

    [latex]\ce{N2O3}(g) \rightleftharpoons2 \ce{NO}(g) + \ce{NO2}(g)[/latex]
    Initial concentration (M) 3.80 0 0
    Change (M) -x +x +x
    Equilibrium concentration (M) 3.80 – x x x

    KP = [latex]\frac{(P_{\ce{NO}})(P_{\ce{NO2}})}{(P_{\ce{N2O3}})}[/latex]
    1.91 = [latex]\frac{x^2}{(3.80 - x)}[/latex]
    7.258 – 1.91 = x2
    0 = x2 + 1.91x -7.258
    0 = ax2 + bx + c
    [latex]\begin{array}{lll} x & = & \frac{-b \pm \sqrt{(b^2) - 4ac}}{2a} \\ & = & \frac{-1.91 \pm \sqrt{(1.91)^2 - 4(1)(-7.258)}}{2(1)} \\ & = & \frac{-1.91 \pm \sqrt{3.648 + 29.032}}{2} \\ & = & \frac{-1.91 \pm \sqrt{32.680}}{2} \\ & = & \frac{-1.91 \pm 5.717}{2} \\ \end{array}[/latex]
    = 1.90 atm or -3.81 atm
    As negative pressure is physically relevant and so the positive root is used. The final pressures are: P[latex]\ce{N2O3}[/latex] = 3.80 – x = 3.80 – 1.90 = 1.90 atm and P[latex]\ce{NO}[/latex] = P[latex]\ce{NO2}[/latex] = x = 1.90 atm

  15. Assume x is negligible, 2.2 × 10-6 = [latex]\frac{\ce{[H2]}\ce{[S2]}}{\ce{[H2S]^2}} = \frac{[2x]^2[x]}{[0.824 - 2x]^2}[/latex]
    [latex]\frac{[2x]^2[x]}{[0.824]^2} = \frac{[4x]^3}{[0.678976]}[/latex] = 2.2 × 10-6
    x = 0.007,  0.007 / 0.824 = 0.008495 or 0.8495%
  16. x = 0.0493 atm, 4.7 × 10-2 = [latex]\frac{\ce{[BrCl]^2}}{\ce{[Br2]}\ce{[Cl2]}} = \frac{[x]^2}{[0.450][0.115]}[/latex]
  17. [latex]\ce{[O2]}[/latex] = 3.70 × 10-4 = [latex]\ce{[HCl]}[/latex] = 1.52 × 10-3 = [latex]\ce{[Cl2]}[/latex] = [latex]\ce{[H2O]}[/latex] = 0.499
  18. [latex]\ce{[NOCl]} = 3.95 \ce{[NO]} = 0.0458 \ce{[Cl2]} =[/latex] 0.0229
  19. The answers are as follows:
    1. Both pressures will increase
    2. [latex]\ce{N2O4}[/latex] = 7.99 atm [latex]\ce{NO}[/latex] = 1.01 atm
  20. Since there are more moles of gas on the products side if we decrease the volume the pressure would then increase. We should then see the mass/moles of the reactants ([latex]\ce{SbCl5}[/latex]) increase and the products ([latex]\ce{SbCl3}[/latex] and [latex]\ce{Cl2}[/latex]) decrease.


14.5 Equilibrium and Thermodynamics [Go to section 14.5]

  1. Calculate the equilibrium constant at 25 °C for each of the following reactions from the value of ΔG° given.
    1. [latex]{\text{I}}_{2}\left(s\right)+{\text{Cl}}_{2}\left(g\right)\longrightarrow \text{2ICl}\left(g\right)\,\,\,\,\,\,\,{;}\,\,\,\,\,\,\,\Delta G^{\circ }=-\text{10.88 kJ}[/latex]
    2. [latex]{\text{H}}_{2}\left(g\right)+{\text{I}}_{2}\left(s\right)\longrightarrow \text{2HI}\left(g\right)\,\,\,\,\,\,\,{;}\,\,\,\,\,\,\,\Delta G^{\circ }=\text{3.4 kJ}[/latex]
    3. [latex]{\text{CS}}_{2}\left(g\right)+{\text{3Cl}}_{2}\left(g\right)\longrightarrow {\text{CCl}}_{4}\left(g\right)+{\text{S}}_{2}{\text{Cl}}_{2}\left(g\right)\,\,\,\,\,\,\,{;}\,\,\,\,\,\,\,\Delta G^{\circ }=-\text{39 kJ}[/latex]
    4. [latex]{\text{2SO}}_{2}\left(g\right)+{\text{O}}_{2}\left(g\right)\longrightarrow {\text{2SO}}_{3}\left(g\right)\,\,\,\,\,\,\,{;}\,\,\,\,\,\,\,\Delta G^{\circ }=-\text{141.82 kJ}[/latex]
    5. [latex]{\text{CS}}_{2}\left(g\right)\longrightarrow {\text{CS}}_{2}\left(l\right)\,\,\,\,\,\,\,{;}\,\,\,\,\,\,\,\Delta G^{\circ }=-\text{1.88 kJ}[/latex]
  2. Calculate ΔG° for each of the following reactions from the equilibrium constant at the temperature given.
    1. [latex]{\text{N}}_{2}\left(g\right)+{\text{O}}_{2}\left(g\right)\longrightarrow \text{2NO}\left(g\right)\,\,\,{;}\,\,\,\text{T}=2000^{\circ}\text{C}\,\,\,{;}\,\,\,{K}_{p}=4.1\times {10}^{-\text{4}}[/latex]
    2. [latex]{\text{H}}_{2}\left(g\right)+{\text{I}}_{2}\left(g\right)\longrightarrow \text{2HI}\left(g\right)\,\,\,{;}\,\,\,\text{T}=400^{\circ}\text{C}\,\,\,{;}\,\,\,{K}_{p}=50.0[/latex]
    3. [latex]{\text{CO}}_{2}\left(g\right)+{\text{H}}_{2}\left(g\right)\longrightarrow \text{CO}\left(g\right)+{\text{H}}_{2}\text{O}\left(g\right)\,\,\,{;}\,\,\,\text{T}=980^{\circ}\text{C}\,\,\,{;}\,\,\,{K}_{p}=1.67[/latex]
    4. [latex]{\text{CaCO}}_{3}\left(s\right)\longrightarrow \text{CaO}\left(s\right)+{\text{CO}}_{2}\left(g\right)\,\,\,{;}\,\,\,\text{T}=900^{\circ}\text{C}\,\,\,{;}\,\,\,{K}_{p}=1.04[/latex]
    5. [latex]\text{HF}\left(aq\right)+{\text{H}}_{2}\text{O}\left(l\right)\longrightarrow {\text{H}}_{3}{\text{O}}^{\text{+}}\left(aq\right)+{\text{F}}^{-}\left(aq\right)\,\,\,{;}\,\,\,\text{T}=25^{\circ}\text{C}\,\,\,{;}\,\,\,{K}_{p}=7.2\times {10}^{-\text{4}}[/latex]
    6. [latex]\text{AgBr}\left(s\right)\longrightarrow {\text{Ag}}^{\text{+}}\left(aq\right)+{\text{Br}}^{-}\left(aq\right)\,\,\,{;}\,\,\,\text{T}=25^{\circ}\text{C}\,\,\,{;}\,\,\,{K}_{p}=3.3\times {10}^{-\text{13}}[/latex]
  3. Calculate ΔG° in kJ for each of the following reactions from the equilibrium constant at the temperature given.
    1. [latex]{\text{CH}}_{3}{\text{NH}}_{2}\left(aq\right)+{\text{H}}_{2}\text{O}\left(l\right)\longrightarrow {\text{CH}}_{3}{\text{NH}}_{3}{}^{\text{+}}\left(aq\right)+{\text{OH}}^{-}\left(aq\right)\,\,\,{;}\,\,\,\text{T}=25^{\circ}\text{C}\,\,\,{;}\,\,\,{K}_{p}=4.4\times {10}^{-\text{4}}[/latex].
    2. [latex]{\text{PbI}}_{2}\left(s\right)\longrightarrow {\text{Pb}}^{2+}\left(aq\right)+{\text{2I}}^{-}\left(aq\right)\,\,\,{;}\,\,\,\text{T}=25^{\circ}\text{C}\,\,\,{;}\,\,\,{K}_{p}=8.7\times {10}^{-\text{9}}[/latex]
  4. Calculate the equilibrium constant for the following reactions given the ΔG° and the temperature
    1. [latex]\text{2LiOH}\left(s\right)+{\text{CO}}_{2}\left(g\right)\longrightarrow {\text{Li}}_{2}{\text{CO}}_{3}\left(s\right)+{\text{H}}_{2}\text{O}\left(g\right)\,\,\,\,\,\,\,{;}\,\,\,\,\,\,\,\Delta G^{\circ }=-\text{79 kJ}[/latex] T = 25°C
    2. [latex]{\text{N}}_{2}{\text{O}}_{3}\left(g\right)\longrightarrow \text{NO}\left(g\right)+{\text{NO}}_{2}\left(g\right)\,\,\,\,\,\,\,{;}\,\,\,\,\,\,\,\Delta G^{\circ }=-\text{1.6 kJ}[/latex]
    3. [latex]{\text{SnCl}}_{4}\left(l\right)\longrightarrow {\text{SnCl}}_{4}\left(l\right)\,\,\,\,\,\,\,{;}\,\,\,\,\,\,\,\Delta G^{\circ }=\text{8.0 kJ}[/latex] T = 25°C
  5. Calculate the equilibrium constant at the temperature given.
    1. [latex]{\text{I}}_{2}\left(s\right)+{\text{Cl}}_{2}\left(g\right)\longrightarrow \text{2ICl}\left(g\right)\,\,\,\,\,\,\,{;}\,\,\,\,\,\,\,\left(\text{T}=100^{\circ C}\right)[/latex]
    2. [latex]{\text{H}}_{2}\left(g\right)+{\text{I}}_{2}\left(s\right)\longrightarrow \text{2HI}\left(g\right)\,\,\,\,\,\,\,{;}\,\,\,\,\,\,\,\left(\text{T}=0.0^{\circ C}\right)[/latex]
    3. [latex]{\text{CS}}_{2}\left(g\right)+{\text{3Cl}}_{2}\left(g\right)\longrightarrow {\text{CCl}}_{4}\left(g\right)+{\text{S}}_{2}{\text{Cl}}_{2}\left(g\right)\,\,\,\,\,\,\,{;}\,\,\,\,\,\,\,\left(\text{T}=125^{\circ C}\right)[/latex]
    4. [latex]{\text{2SO}}_{2}\left(g\right)+{\text{O}}_{2}\left(g\right)\longrightarrow {\text{2SO}}_{3}\left(g\right)\,\,\,\,\,\,\,{;}\,\,\,\,\,\,\,\left(\text{T}=675^{\circ C}\right)[/latex]
    5. [latex]{\text{CS}}_{2}\left(g\right)\longrightarrow {\text{CS}}_{2}\left(l\right)\,\,\,\,\,\,\,{;}\,\,\,\,\,\,\,\left(\text{T}=90^{\circ C}\right)[/latex]
  6. Calculate the equilibrium constant at the temperature given.
    1. [latex]{\text{O}}_{2}\left(g\right)+{\text{2F}}_{2}\left(g\right)\longrightarrow {\text{2F}}_{2}\text{O}\left(g\right)\,\,\,\,\,\,\,{;}\,\,\,\,\,\,\,\left(\text{T}=100^{\circ C}\right)[/latex]
    2. [latex]{\text{I}}_{2}\left(s\right)+{\text{Br}}_{2}\left(l\right)\longrightarrow \text{2IBr}\left(g\right)\,\,\,\,\,\,\,{;}\,\,\,\,\,\,\,\left(\text{T}=0.0^{\circ C}\right)[/latex]
    3. [latex]\text{2LiOH}\left(s\right)+{\text{CO}}_{2}\left(g\right)\longrightarrow {\text{Li}}_{2}{\text{CO}}_{3}\left(s\right)+{\text{H}}_{2}\text{O}\left(g\right)\,\,\,\,\,\,\,{;}\,\,\,\,\,\,\,\left(\text{T}=575^{\circ C}\right)[/latex]
    4. [latex]{\text{N}}_{2}{\text{O}}_{3}\left(g\right)\longrightarrow \text{NO}\left(g\right)+{\text{NO}}_{2}\left(g\right)\,\,\,\,\,\,\,{;}\,\,\,\,\,\,\,\left(\text{T}=-10.0^{\circ C}\right)[/latex]
    5. [latex]{\text{SnCl}}_{4}\left(l\right)\longrightarrow {\text{SnCl}}_{4}\left(g\right)\,\,\,\,\,\,\,{;}\,\,\,\,\,\,\,\left(\text{T}=200^{\circ C}\right)[/latex]
  7. At room temperature, the equilibrium constant (Kw) for the self-ionization of water is 1.00 [latex]\times[/latex] 10−14. Using this information, calculate the standard free energy change for the aqueous reaction of hydrogen ion with hydroxide ion to produce water. (Hint: The reaction is the reverse of the self-ionization reaction.)
  8. Consider the following reaction at 298 K: [latex]{\text{N}}_{2}{\text{O}}_{4}\left(g\right)\rightleftharpoons {\text{2NO}}_{2}\left(g\right){K}_{P}=0.142[/latex] What is the standard free energy change at this temperature? Describe what happens to the initial system, where the reactants and products are in standard states, as it approaches equilibrium.
  9. Consider the decomposition of [latex]\ce{CaCO3}(s)[/latex] into [latex]\ce{CaO}(s)[/latex] and [latex]\ce{CO2}(g)[/latex]. What is the equilibrium partial pressure of [latex]\ce{CO2}[/latex] at room temperature?
  10. Hydrogen sulfide is a pollutant found in natural gas. Following its removal, it is converted to sulfur by the reaction [latex]{\text{2H}}_{2}\text{S}\left(g\right)+{\text{SO}}_{2}\left(g\right)\rightleftharpoons \frac{3}{8}{\text{S}}_{8}\left(s,\text{rhombic}\right)+{\text{2H}}_{2}\text{O}\left(l\right)[/latex]. What is the equilibrium constant for this reaction? Is the reaction endothermic or exothermic?
  11. Benzene can be prepared from acetylene. [latex]{\text{3C}}_{2}{\text{H}}_{2}\left(g\right)\rightleftharpoons {\text{C}}_{6}{\text{H}}_{6}\left(g\right)[/latex]. Determine the equilibrium constant at 25 °C and at 850 °C. Is the reaction spontaneous at either of these temperatures? Why is all acetylene not found as benzene?
  12. In the laboratory, hydrogen chloride ([latex]\ce{HCl}(g)[/latex]) and ammonia ([latex]\ce{NH3}(g)[/latex]) often escape from bottles of their solutions and react to form the ammonium chloride ([latex]\ce{NH4Cl}(s)[/latex]), the white glaze often seen on glassware. Assuming that the number of moles of each gas that escapes into the room is the same, what is the maximum partial pressure of [latex]\ce{HCl}[/latex] and [latex]\ce{NH3}[/latex] in the laboratory at room temperature? (Hint: The partial pressures will be equal and are at their maximum value when at equilibrium.)
  13. Carbon tetrachloride, an important industrial solvent, is prepared by the chlorination of methane at 850 K. [latex]{\text{CH}}_{4}\left(g\right)+{\text{4Cl}}_{2}\left(g\right)\longrightarrow {\text{CCl}}_{4}\left(g\right)+\text{4HCl}\left(g\right)[/latex] What is the equilibrium constant for the reaction at 850 K? Would the reaction vessel need to be heated or cooled to keep the temperature of the reaction constant?
  14. Carbon dioxide decomposes into [latex]\ce{CO}[/latex] and [latex]\ce{O2}[/latex] at elevated temperatures. What is the equilibrium partial pressure of oxygen in a sample at 1000 °C for which the initial pressure of [latex]\ce{CO2}[/latex] was 1.15 atm?
  15. Acetic acid, [latex]\ce{CH3CO2H}[/latex], can form a dimer, [latex]\ce{(CH3CO2H)2}[/latex], in the gas phase.
    [latex]{\text{2CH}}_{3}{\text{CO}}_{2}\text{H}\left(g\right)\longrightarrow {\left({\text{CH}}_{3}{\text{CO}}_{2}\text{H}\right)}_{2}\left(g\right)[/latex]
    The dimer is held together by two hydrogen bonds with a total strength of 66.5 kJ per mole of dimer.  At 25 °C, the equilibrium constant for the dimerization is 1.3 [latex]\times[/latex] 103 (pressure in atm). What is ΔS° for the reaction?
  16. The evaporation of one mole of water at 298 K has a standard free energy change of 8.58 kJ. [latex]{\text{H}}_{2}\text{O}\left(l\right)\rightleftharpoons {\text{H}}_{2}\text{O}\left(g\right)\Delta {G}_{298}^{\circ }=\text{8.58 kJ}[/latex]
    1. Is the evaporation of water under standard thermodynamic conditions spontaneous?
    2. Determine the equilibrium constant, KP, for this physical process.
    3. By calculating ∆G, determine if the evaporation of water at 298 K is spontaneous when the partial pressure of water, [latex]{P}_{{\text{H}}_{2}\text{O}}[/latex], is 0.011 atm.
    4. If the evaporation of water were always nonspontaneous at room temperature, wet laundry would never dry when placed outside. In order for laundry to dry, what must be the value of [latex]{P}_{{\text{H}}_{2}\text{O}}[/latex] in the air?
Show Selected Solutions
  1. The answers are as follows:
    1. ln K = [latex]\frac{-10880}{-8.314(298.15)}[/latex] = 4.389, K = 80.57
    2. ln K = [latex]\frac{3400}{-8.314(298.15)}[/latex] = -1.372, K = 0.25;
    3. ln K = [latex]\frac{-39,000}{-8.314(298.15)}[/latex] = 15.73, K = 6.8 × 106;
    4. ln K = [latex]\frac{-141,820}{-8.314(298.15)}[/latex] = 57.2127, K = 7.034 × 1024;
    5. ln K = [latex]\frac{-1880}{-8.314(298.15)}[/latex] = 0.758, K = 2.13
  2. The answers are as follows:
    1. -19 kJ
    2. -46 kJ
  3. The answers are as follows:
    1. [latex]\begin{array}{lll} \Delta Hº_{298} & = & 2\Delta Hº_{f_{\ce{ICl}(g)}} - \Delta Hº_{f_{\ce{I2}(s)}} - \Delta Hº_{f_{\ce{Cl2}(g)}} = 35.6 \text{ kJ } = 2(17.8) - 0 - 0 = 35.6 \text{ kJ} \\ \Delta Sº & = & 2\Delta Sº_{\ce{ICl}(g)} - \Delta Sº_{\ce{I2}(s)} - \Delta Sº_{\ce{Cl2}(g)} = 2(247.44) - 116.14 - 222.96 = 155.78 \text{ J K}^{-1} \\ \Delta G & = & \Delta Hº_{298} - T\Delta Sº = 35,600 \text{ J } - (373.15 \text{ K})(155.78 \text{ J K}^{-1}) = -2.25 × 10^4 \text{ J} \\ \text{ln } K & = & \frac{\Delta G}{-RT} = \frac{-22,500}{-8.314(373.15)} = 7.253, K = 1.41 × 10^3 \\ \end{array}[/latex]
    2. [latex]\begin{array}{lll} \Delta Hº_{298} & = & 2\Delta Hº_{f_{\ce{HI}(g)}} - \Delta Hº_{f_{\ce{H2}(g)}} - \Delta Hº_{f_{\ce{I2}(s)}} = 2(26.5) - 0 - 0 = 53.0 \text{ kJ} \\ \Delta Sº & = & 2\Delta Sº_{\ce{HI}(g)} - \Delta Sº_{\ce{H2}(g)} - \Delta Sº_{\ce{I2}(s)} = 2(206.48) - 130.57 - 116.14 = 166.25 \text{ J K}^{-1} \\ \Delta G & = & \Delta Hº_{298} - T\Delta Sº = 53,000 - 273.15(166.25) = 7.59 × 10^3 \text{ J} \\ \text{ln } K & = & \frac{\Delta G}{-RT} = \frac{7.59 × 10^3}{-8.314(373.15)} = -2.447, K = 0.0866 \\ \end{array}[/latex]
    3. [latex]\begin{array}{lll} \Delta Hº_{298} & = & 2\Delta Hº_{f_{\ce{CCl4}(g)}} + \Delta Hº_{f_{\ce{S2Cl2}(g)}} - \Delta Hº_{f_{\ce{CS2}(g)}} - 3\Delta Hº_{f_{\ce{Cl2}}} = -102.9 + (-18) -117.4 - 3(0) = -238 \text{ kJ} \\ \Delta Sº & = & 2\Delta Sº_{\ce{CCl4}(g)} + \Delta Sº_{\ce{S2Cl2}(g)} - \Delta Sº_{\ce{CS2}(g)} - 3\Delta Sº_{\ce{Cl2}(g)} = 309.7 + 331.4 - 237.7 - 3(222.96) = -265.5  \text{ J K}^{-1} \\ \Delta G & = & \Delta Hº_{298} - T\Delta Sº = -238,000 - 398.15(-265.5) = -132.29 \text{ kJ } = 1.32 × 10^2 \text{ J} \\ \text{ln } K & = & \frac{\Delta G}{-RT} = \frac{-132,000}{-8.314(373.15)} = 39.9, K = 2.1 × 10^{17} \\ \end{array}[/latex]
    4. [latex]\begin{array}{lll} \Delta Hº_{298} & = & 2\Delta Hº_{f_{\ce{SO3}(g)}} - 2\Delta Hº_{f_{\ce{SO2}(g)}} - \Delta Hº_{f_{\ce{O2}(g)}} = 2(-395.7) - 2(-296.83) - 0 = -197.7 \text{ kJ} \\ \Delta Sº & = & 2\Delta Sº_{\ce{SO3}(g)} - 2\Delta Sº_{\ce{SO2}(g)} - \Delta Sº_{\ce{O2}(g)} = 2(256.6) - 2(248.1) - 205.03 = -188.0  \text{ J K}^{-1} \\ \Delta G & = & \Delta Hº_{298} - T\Delta Sº = -197,700 - 948.15(-188.0) = -19,449 = -1.945 × 10^4 \text{ J} \\ \text{ln } K & = & \frac{\Delta G}{-RT} = \frac{-1.945 × 10^4}{-8.314(373.15)} = 2.467, K = 11.8 \\ \end{array}[/latex]
    5. [latex]\begin{array}{lll} \Delta Hº_{298} & = & 2\Delta Hº_{f_{\ce{CS2}(l)}} - \Delta Hº_{f_{\ce{CS2}(g)}} = 89.71 - 117.4 = -27.7 \text{ kJ} \\ \Delta Sº & = & 2\Delta Sº_{\ce{CS2}(l)} - \Delta Sº_{\ce{CS2}(g)} - \Delta Sº_{\ce{O2}(s)} = 151.3 - 237.7 = -86.4  \text{ J K}^{-1} \\ \Delta G & = & \Delta Hº_{298} - T\Delta Sº = -27,700 -363.15(-86.4) = -3.68 × 10^3 \text{ J} \\ \text{ln } K & = & \frac{\Delta G}{-RT} = \frac{3.68 × 10^3}{-8.314(373.15)} = -1.219, K = 0.296 \\ \end{array}[/latex]
  4. The reverse of the self-ionization reaction is: [latex]\ce{H+}(aq) + \ce{OH-}(aq) \longrightarrow \ce{H2O}(l)[/latex] with K = [latex]\frac{1}{K_w}[/latex] = 1.00 × 10-14. This gives [latex]\Delta Gº_{298} = -RT\text{ln}K = -(8.314 \text{ J K}^{-1})(298.15 \text{ K})(\text{ln } 1.000 × 10^{-14}) = -79.91[/latex] kJ
  5. The relevant equation and equilibrium expression is [latex]\ce{CaCO3}(s) \longrightarrow \ce{CaO}(s) + \ce{CO2}(g)[/latex] Kp = P[latex]\ce{CO2}[/latex]
    ΔG°298 = [latex]\sum v \Delta G°_f(\text{products}) - \sum v \Delta G°_f(\text{reactants})[/latex]
    ΔG°298 = [1 mol(-394.36 kJ/mol) + 1 mol(-603.3 kJ/mol)] – [1 mol(-1081.4 kJ/mol)] = 83.7 kJ
    ΔG°298 = –RTlnK
    83.7 × 103 = -8.314 × 298.15ln K
    K  = 2.2 × 10-15, As Kp = P[latex]\ce{CO2}[/latex] , the partial pressure of [latex]\ce{CO2}[/latex] above [latex]\ce{CaCO3}[/latex] at equilibrium, is 2.2 × 10-15 atm
  6. The equilibrium may be calculated from the standard values of the entropy and entropy change at room temperature: ΔH°298 = -599.27 kJ/mol and ΔS°298 = -333.5 J/mol K. The standard free energy change and equilibrium constant at room temperature is then: ΔG°298 = -499.89 kJ/mol and KP = 4.2 × 1087. At 1123 K (remember to use kelvin temperature) they are: ΔG°298 = -224.75 kJ/mol and KP = 2.8 × 1010. The reaction is spontaneous at both temperatures under standard conditions. While spontaneous, the reaction must be very slow because acetylene is commonly stored for extended periods of time and is used in welding applications.
  7. [latex]\begin{array}{lll} \Delta Hº & = & \Delta Hº_{\ce{CCl4}(g)} + 4(\Delta Hº_{\ce{HCl}(g)}) - \Delta Hº_{\ce{CH4}(g)} - 4(\Delta Hº_{\ce{Cl2}(g)}) \\ & = & (1 \text{ mol})(-102.9 \text{ kJ mol}^{-1}) + (4 \text{ mol})(-92.307 \text{ kJ mol}^{-1}) - (1 \text{ mol})(-74.81 \text{ kJ mol}^{-1}) - (4 \text{ mol})(0 \text{ kJ mol}^{-1}) \\ & = & -397.3 \text{ kJ} \\ \end{array}[/latex]
    [latex]\begin{array}{lll} \Delta Sº & = & \Delta Sº_{\ce{CCl4}(g)} + 4(\Delta Sº_{\ce{HCl}(g)}) - \Delta Sº_{\ce{CH4}(g)} - 4(\Delta Sº_{\ce{Cl2}(g)}) \\ & = & (1 \text{ mol})(309.7 \text{ J K}^{-1} \text{ mol}^{-1}) + (4 \text{ mol})(-186.80 \text{ J K}^{-1} \text{ mol}^{-1}) - (1 \text{ mol})(186.15 \text{ J K}^{-1} \text{ mol}^{-1}) - (4 \text{ mol})(222.96 \text{ J K}^{-1} \text{ mol}^{-1}) \\ & = & -21.1 \text{ J K}^{-1} \text{ mol}^{-1} \\ \end{array}[/latex]
    ΔG° = (-397,300 J) – (850 K)(-21.1 J K-1) = 379,400 J = -379.4 kJ
    Two valid ways of calculating K give slightly different answers because of rounding errors.
    log K=[latex]\frac{-379,400 \text{ J}}{(-2.303)(8.314 \text{ J K}^{-1})(850 \text{ K})}[/latex] = +23.31, K = 2.04 × 1023
    or ln K  = [latex]\frac{-379,400 \text{ J}}{-(8.314 \text{ J K}^{-1})(850 \text{ K})}[/latex] = 53.39, K = 2.07 × 1023
    ΔH° is negative, so the reaction is exothermic and must be cooled to maintain constant temperature.
  8. The enthalpy of the reaction should be –66.5 kJ from the strength of the hydrogen bonds of the dimer. We can solve for Gibb’s Free Energy from the equilibrium constant ΔG = –RT lnK,  ΔG = -17.8 kJ, ΔG = ΔH – TΔS, -17.8 kJ = -66.5 kJ – 298ΔS, ΔS = -163.5 J


License

Icon for the Creative Commons Attribution-NonCommercial-ShareAlike 4.0 International License

Chemistry Fundamentals Copyright © by Dr. Julie Donnelly, Dr. Nicole Lapeyrouse, and Dr. Matthew Rex is licensed under a Creative Commons Attribution-NonCommercial-ShareAlike 4.0 International License, except where otherwise noted.

Share This Book