3.4 The Wavelength Nature of Matter – Chemistry LibreTexts

website:
https://chem.libretexts.org/Bookshelves/General_Chemistry/Map%3A_A_Molecular_Approach_(Tro)/07%3A_The_Quantum-Mechanical_Model_of_the_Atom/7.04%3A_The_Wavelength_Nature_of_Matter

Bohr’s model explained the experimental data for the hydrogen atom and was widely accepted, but it also raised many questions. Why did electrons orbit at only fixed distances defined by a single quantum number n = 1, 2, 3, and so on, but never in between? Why did the model work so well describing hydrogen and one-electron ions, but could not correctly predict the emission spectrum for helium or any larger atoms? To answer these questions, scientists needed to completely revise the way they thought about matter.

Behavior in the Microscopic World

We know how matter behaves in the macroscopic world—objects that are large enough to be seen by the naked eye follow the rules of classical physics. A billiard ball moving on a table will behave like a particle: It will continue in a straight line unless it collides with another ball or the table cushion, or is acted on by some other force (such as friction). The ball has a well-defined position and velocity (or a well-defined momentum, p = mv, defined by mass m and velocity v) at any given moment. In other words, the ball is moving in a classical trajectory. This is the typical behavior of a classical object.

When waves interact with each other, they show interference patterns that are not displayed by macroscopic particles such as the billiard ball. For example, interacting waves on the surface of water can produce interference patters similar to those shown on Figure 3.4.1. This is a case of wave behavior on the macroscopic scale, and it is clear that particles and waves are very different phenomena in the macroscopic realm.

As technological improvements allowed scientists to probe the microscopic world in greater detail, it became increasingly clear by the 1920s that very small pieces of matter follow a different set of rules from those we observe for large objects. The unquestionable separation of waves and particles was no longer the case for the microscopic world.

One of the first people to pay attention to the special behavior of the microscopic world was Louis de Broglie. He asked the question: If electromagnetic radiation can have particle-like character, can electrons and other submicroscopic particles exhibit wavelike character? In his 1925 doctoral dissertation, de Broglie extended the wave–particle duality of light that Einstein used to resolve the photoelectric-effect paradox to material particles. He predicted that a particle with mass m and velocity v (that is, with linear momentum p) should also exhibit the behavior of a wave with a wavelength value [latex]\lambda[/latex], given by this expression in which h is the familiar Planck’s constant:

[latex]\lambda =\dfrac{h}{mv}=\dfrac{h}{p}[/latex]

This is called the de Broglie wavelength. Unlike the other values of [latex]\lambda[/latex] discussed in this chapter, the de Broglie wavelength is a characteristic of particles and other bodies, not electromagnetic radiation (note that this equation involves velocity [v, m/s], not frequency [[latex]\nu[/latex], Hz]. Although these two symbols are identical, they mean very different things). Where Bohr had postulated the electron as being a particle orbiting the nucleus in quantized orbits, de Broglie argued that Bohr’s assumption of quantization can be explained if the electron is considered not as a particle, but rather as a circular standing wave such that only an integer number of wavelengths could fit exactly within the orbit (Figure 3.4.2).

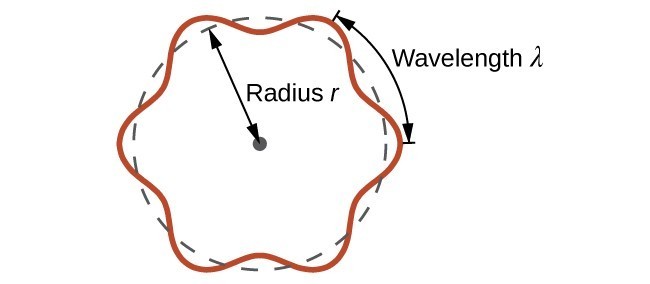
For a circular orbit of radius r, the circumference is [latex]2\pi{r}[/latex], and so de Broglie’s condition is:

2[latex]\pi[/latex] r=n[latex]\lambda[/latex] ,n=1,2,3,  . . .

Standing Waves

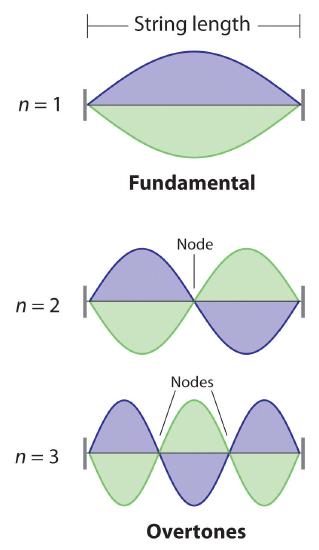
De Broglie also investigated why only certain orbits were allowed in Bohr’s model of the hydrogen atom. He hypothesized that the electron behaves like a standing wave (a wave that does not travel in space). An example of a standing wave is the motion of a string of a violin or guitar. When the string is plucked, it vibrates at certain fixed frequencies because it is fastened at both ends (Figure 3.4.3). If the length of the string is L, then the lowest-energy vibration (the fundamental) has wavelength

[latex]\begin{align} \dfrac{\lambda }{2} & =L \nonumber \\ \lambda &= 2L \nonumber \end{align} \label{6.4.4}[/latex]

Higher-energy vibrations are called overtones (the vibration of a standing wave that is higher in energy than the fundamental vibration) and are produced when the string is plucked more strongly; they have wavelengths given by

[latex]\lambda=\dfrac{2L}{n} \label{6.4.5}[/latex]

where n has any integral value. When plucked, all other frequencies die out immediately. Only the resonant frequencies survive and are heard. Thus, we can think of the resonant frequencies of the string as being quantized. Notice in Figure 3.4.3 that all overtones have one or more nodes, points where the string does not move. The amplitude of the wave at a node is zero.

Quantized vibrations and overtones containing nodes are not restricted to one-dimensional systems, such as strings. A two-dimensional surface, such as a drumhead, also has quantized vibrations. Similarly, when the ends of a string are joined to form a circle, the only allowed vibrations are those with wavelength

[latex]2πr = n\lambda \label{6.4.6}[/latex]

where r is the radius of the circle. De Broglie argued that Bohr’s allowed orbits could be understood if the electron behaved like a standing circular wave (Figure 3.4.4). The standing wave could exist only if the circumference of the circle was an integral multiple of the wavelength such that the propagated waves were all in phase, thereby increasing the net amplitudes and causing constructive interference. Otherwise, the propagated waves would be out of phase, resulting in a net decrease in amplitude and causing destructive interference. The nonresonant waves interfere with themselves! De Broglie’s idea explained Bohr’s allowed orbits and energy levels nicely: in the lowest energy level, corresponding to n = 1 above, one complete wavelength would close the circle. Higher energy levels would have successively higher values of n with a corresponding number of nodes.

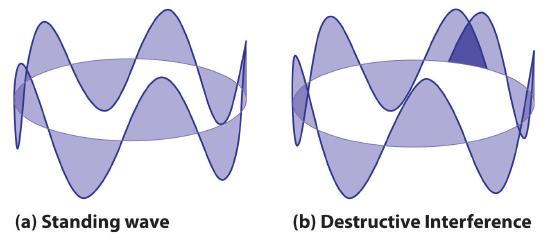
Like all analogies, although the standing wave model helps us understand much about why Bohr’s theory worked, it also, if pushed too far, can mislead. As you will see, some of de Broglie’s ideas are retained in the modern theory of the electronic structure of the atom: the wave behavior of the electron and the presence of nodes that increase in number as the energy level increases. Unfortunately, his (and Bohr’s) explanation also contains one major feature that we now know to be incorrect: in the currently accepted model, the electron in a given orbit is not always at the same distance from the nucleus.

The Heisenberg Uncertainty Principle

Because a wave is a disturbance that travels in space, it has no fixed position. One might therefore expect that it would also be hard to specify the exact position of a particle that exhibits wavelike behavior. A characteristic of light is that is can be bent or spread out by passing through a narrow slit. You can literally see this by half closing your eyes and looking through your eye lashes. This reduces the brightness of what you are seeing and somewhat fuzzes out the image, but the light bends around your lashes to provide a complete image rather than a bunch of bars across the image. This is called diffraction.

This behavior of waves is captured in Maxwell’s equations (1870 or so) for electromagnetic waves and was and is well understood. An “uncertainty principle” for light is, if you will, merely a conclusion about the nature of electromagnetic waves and nothing new. De Broglie’s idea of wave-particle duality means that particles such as electrons which exhibit wavelike characteristics will also undergo diffraction from slits whose size is on the order of the electron wavelength.

This situation was described mathematically by the German physicist Werner Heisenberg (1901–1976; Nobel Prize in Physics, 1932), who related the position of a particle to its momentum. Referring to the electron, Heisenberg stated that “at every moment the electron has only an inaccurate position and an inaccurate velocity, and between these two inaccuracies there is this u certainty relation.” Mathematically, the Heisenberg uncertainty principle states that the uncertainty in the position of a particle ([latex]\Delta[/latex]x) multiplied by the uncertainty in its mometum [[latex]\Delta[/latex](mv)] is greater than or equal to Planck’s constant divided by 4[latex]\pi[/latex]:

[latex]\left ( \Delta x \right )\left ( \Delta \left [ mv \right ] \right )\ge \dfrac{h}{4\pi } \label{6.4.7}[/latex]

Because Planck’s constant is a very small number, the Heisenberg uncertainty principle is important only for particles such as electrons that have very low masses. These are the same particles predicted by de Broglie’s equation to have measurable wavelengths.

If the precise position x of a particle is known absolutely ([latex]\Delta[/latex]x = 0), then the uncertainty in its momentum must be infinite:

[latex]\left ( \Delta \left [ mv \right ] \right )= \dfrac{h}{4\pi \left ( \Delta x \right ) }=\dfrac{h}{4\pi \left ( 0 \right ) }=\infty \label{6.4.8}[/latex]

Because the mass of the electron at rest (m) is both constant and accurately known, the uncertainty in [latex]\Delta[/latex](mv) must be due to the [latex]\Delta[/latex]v term, which would have to be infinitely large for [latex]\Delta[/latex](mv) to equal infinity. That is, according to the equation above, the more accurately we know the exact position of the electron (as [latex]\Delta[/latex]x [latex]\ce{->}[/latex] 0), the less accurately we know the speed and the kinetic energy of the electron ([latex]\frac{1}{2}mv^2[/latex]) because [latex]\Delta[/latex](mv) [latex]\ce{->}[/latex] ∞. Conversely, the more accurately we know the precise momentum (and the energy) of the electron [as [latex]\Delta[/latex](mv) [latex]\ce{->}[/latex] 0], then [latex]\Delta[/latex]x [latex]\ce{->}[/latex] ∞ and we have no idea where the electron is.

Bohr’s model of the hydrogen atom violated the Heisenberg uncertainty principle by trying to specify simultaneously both the position (an orbit of a particular radius) and the energy (a quantity related to the momentum) of the electron. Moreover, given its mass and wavelike nature, the electron in the hydrogen atom could not possibly orbit the nucleus in a well-defined circular path as predicted by Bohr. You will see, however, that the most probable radius of the electron in the hydrogen atom is exactly the one predicted by Bohr’s model.

Glossary

de Broglie wavelength: The wavelength (λ) that is associated with an object in relation to its momentum and mass

Standing wave: A wave that does not travel in space

Constructive interference: The interference of two or more waves of equal frequency and are in phase thereby increasing the net amplitudes

Destructive interference: The propagated waves would be out of phase, resulting in a net decrease in amplitude and causing

Heisenberg uncertainty principle: States that the uncertainty in the position of a particle is impossible to describe both the location and speed of particles that exhibit wave like behavior

Contributors and Attributions