Chapter 12: Solutions and Colloids

12.6 Colligative Properties of Electrolyte Solutions

Learning Outcomes

  • Explain and calculate properties of solutions containing an electrolyte as a solute

Colligative Properties of Electrolytes

As noted previously in this chapter, the colligative properties of a solution depend only on the number, not on the identity, of solute species dissolved. The concentration terms in the equations for various colligative properties (freezing point depression, boiling point elevation, osmotic pressure) pertain to all solute species present in the solution. For the solutions considered thus far in this chapter, the solutes have been nonelectrolytes that dissolve physically without dissociation or any other accompanying process. Each molecule that dissolves yields one dissolved solute molecule. The dissolution of an electroyte, however, is not this simple, as illustrated by the two common examples below:

dissociation [latex]\ce{ NaCl}(s) \rightarrow \ce{Na+} (aq) + \ce{Cl-} (aq)[/latex]

ionization [latex]\ce{HCL}(aq) + \ce{H2O} (l) \rightarrow \ce{Cl-}(aq) + \ce{H3+}(aq)[/latex]

Considering the first of these examples, and assuming complete dissociation, a 1.0 m aqueous solution of NaCl contains 2.0 mole of ions (1.0 mol [latex]\ce{Na+}[/latex] and 1.0 mol [latex]\ce{Cl-}[/latex]) per each kilogram of water, and its freezing point depression is expected to be

[latex]\Delta{T}_{\text{f}}=2.0\text{mol ions/kg water}\times 1.86^{\circ}\text{C kg water/mol ion}=3.7^{\circ}\text{C}[/latex]

When this solution is actually prepared and its freezing point depression measured, however, a value of 3.4 °C is obtained. Similar discrepancies are observed for other ionic compounds, and the differences between the measured and expected colligative property values typically become more significant as solute concentrations increase. These observations suggest that the ions of sodium chloride (and other strong electrolytes) are not completely dissociated in solution.

To account for this and avoid the errors accompanying the assumption of total dissociation, an experimentally measured parameter named in honor of Nobel Prize-winning German chemist Jacobus Henricus van’t Hoff is used. The van’t Hoff factor (i) is defined as the ratio of solute particles in solution to the number of formula units dissolved:

[latex]i=\dfrac{\text{moles of particles in solution}}{\text{moles of formula units dissolved}}[/latex]

Values for measured van’t Hoff factors for several solutes, along with predicted values assuming complete dissociation, are shown in Table 12.6.1.

Table 12.6.1. Expected and Observed van’t Hoff Factors for Several 0.050 m Aqueous Electrolyte Solutions
Electrolyte Particles in Solution i (Predicted) i (Measured)
[latex]\ce{HCl}[/latex] [latex]\ce{H+}[/latex], [latex]\ce{Cl-}[/latex] 2 1.9
[latex]\ce{NaCl}[/latex] [latex]\ce{Na+}[/latex], [latex]\ce{Cl-}[/latex] 2 1.9
[latex]\ce{MgSO4}[/latex] [latex]\ce{Mg^2+}[/latex], [latex]\ce{SO4^2-}[/latex] 2 1.3
[latex]\ce{MgCl2}[/latex] [latex]\ce{Mg^2+}[/latex], [latex]\ce{2Cl-}[/latex] 3 2.7
[latex]\ce{FeCl3}[/latex] [latex]\ce{Fe^3+}[/latex], [latex]\ce{3Cl-}[/latex] 4 3.4
glucose[1] [latex]\ce{C_{12}H_{22}O_{11}}[/latex] 1 1.0

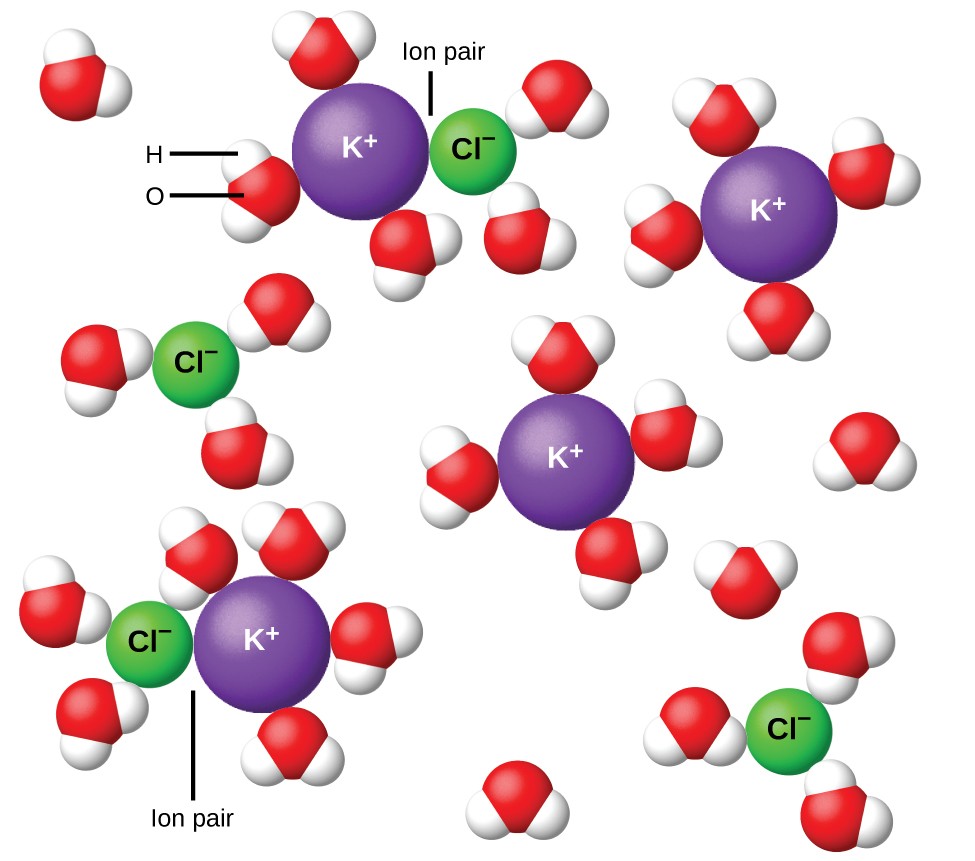
The diagram shows four purple spheres labeled K superscript plus and four green spheres labeled C l superscript minus dispersed in H subscript 2 O as shown by clusters of single red spheres with two white spheres attached. Red spheres represent oxygen and white represent hydrogen. In two locations, the purple and green spheres are touching. In these two locations, the diagram is labeled ion pair. All red and green spheres are surrounded by the white and red H subscript 2 O clusters. The white spheres are attracted to the purple spheres and the red spheres are attracted to the green spheres.
Figure 12.6.1. Ions become more and more widely separated the more dilute the solution, and the residual interionic attractions become less.

In 1923, the chemists Peter Debye and Erich Hückel proposed a theory to explain the apparent incomplete ionization of strong electrolytes. They suggested that although interionic attraction in an aqueous solution is very greatly reduced by solvation of the ions and the insulating action of the polar solvent, it is not completely nullified. The residual attractions prevent the ions from behaving as totally independent particles (Figure 12.6.1). In some cases, a positive and negative ion may actually touch, giving a solvated unit called an ion pair. Thus, the activity, or the effective concentration, of any particular kind of ion is less than that indicated by the actual concentration. Ions become more and more widely separated the more dilute the solution, and the residual interionic attractions become less and less. Thus, in extremely dilute solutions, the effective concentrations of the ions (their activities) are essentially equal to the actual concentrations. Note that the van’t Hoff factors for the electrolytes in Table 12.6.1 are for 0.05 m solutions, at which concentration the value of i for NaCl is 1.9, as opposed to an ideal value of 2.

Example 12.6.1: The Freezing Point of a Solution of an Electrolyte

The concentration of ions in seawater is approximately the same as that in a solution containing 4.2 g of [latex]\ce{NaCl}[/latex] dissolved in 125 g of water. Assume that each of the ions in the [latex]\ce{NaCl}[/latex] solution has the same effect on the freezing point of water as a nonelectrolyte molecule, and determine the freezing temperature the solution (which is approximately equal to the freezing temperature of seawater).

Show Solution

We can solve this problem using the following series of steps.
This is a diagram with six boxes oriented horizontally and linked together with arrows numbered 1 to 5 pointing from each box in succession to the next one to the right. The first box is labeled, “Mass of N a C l.” Arrow 1 points from this box to a second box labeled, “Moles of N a C l.” Arrow 2 points from this box to to a third box labeled, Moles of ions.” Arrow labeled 3 points from this box to a fourth box labeled, “Molality of solution.” Arrow 4 points to a fifth box labeled, “Change in freezing point.” Arrow 5 points to a sixth box labeled, “New freezing point.”

  1. Convert from grams to moles of [latex]\ce{NaCl}[/latex] using the molar mass of [latex]\ce{NaCl}[/latex] in the unit conversion factor: 0.072 mol [latex]\ce{NaCl}[/latex]
  2. Determine the number of moles of ions present in the solution using the number of moles of ions in 1 mole of [latex]\ce{NaCl}[/latex] as the conversion factor (2 mol ions/1 mol [latex]\ce{NaCl}[/latex]): 0.14 mol ions
  3. Determine the molality of the ions in the solution from the number of moles of ions and the mass of solvent, in kilograms: 1.1 m
  4. Use the direct proportionality between the change in freezing point and molal concentration to determine how much the freezing point changes: 2.0 °C
  5. Determine the new freezing point from the freezing point of the pure solvent and the change: -2.0 °C. Check each result as a self-assessment.

Check Your Learning

Key Concepts and Summary

Ionic compounds may not completely dissociate in solution due to activity effects, in which case observed colligative effects may be less than predicted.

Try It

  1. Arrange the following solutions in order by their decreasing freezing points: 0.1 m [latex]\ce{Na3PO4}[/latex], 0.1 m [latex]\ce{C2H5OH}[/latex], 0.01 m [latex]\ce{CO2}[/latex], 0.15 m [latex]\ce{NaCl}[/latex], and 0.2 m [latex]\ce{CaCl2}[/latex].
  2. What is the boiling point of a solution of [latex]\ce{NaCl}[/latex] in water if the solution freezes at -0.93 °C?
Show Selected Solutions

6. Find the molality of the solution from the freezing point depression. Using that value, determine the boiling point elevation and then the boiling point.

[latex]\begin{array}{l}\Delta{T}_{\text{f}}=|0.0^{\circ}\text{C}-0.93^{\circ}\text{C}|=0.93^{\circ}\text{C}={k}_{\text{f}}m=1.86^{\circ}\text{C}{m}^{\text{-1}}\times m\\ m\ce{NaCl}=\frac{0.93^{\circ}\text{C}}{1.86^{\circ}\text{C}{m}^{-1}}=0.50m\end{array}[/latex]

[latex]\Delta[/latex]Tb = Kbm = 0.512 °C m−1 × 0.50 m = 0.256 °C

The boiling point of pure water is 100.00 °C. Addition gives 100.00 °C + 0.26 °C = 100.26 °C.

Glossary

activity: effective concentration of ions in solution; it is lower than the actual concentration, due to ionic interactions.

van’t Hoff factor (i): the ratio of the number of moles of particles in a solution to the number of moles of formula units dissolved in the solution

  1. A nonelectrolyte shown for comparison. ↵
definition

License

Icon for the Creative Commons Attribution-NonCommercial-ShareAlike 4.0 International License

Chemistry Fundamentals Copyright © by Dr. Julie Donnelly, Dr. Nicole Lapeyrouse, and Dr. Matthew Rex is licensed under a Creative Commons Attribution-NonCommercial-ShareAlike 4.0 International License, except where otherwise noted.

Share This Book