Chapter 17: Electrochemistry
17.4 Potential, Free Energy, and Equilibrium
Learning Outcomes
- Explain the relations between potential, free energy change, and equilibrium constants
- Perform calculations involving the relations between cell potentials, free energy changes, and equilibrium
- Use the Nernst equation to determine cell potentials under nonstandard conditions
So far in this chapter, the relationship between the cell potential and reaction spontaneity has been described, suggesting a link to the free energy change for the reaction (see chapter on thermodynamics). The interpretation of potentials as measures of oxidant strength was presented, bringing to mind similar measures of acid-base strength as reflected in equilibrium constants (see the chapter on acid-base equilibria). This section provides a summary of the relationships between potential and the related thermodynamic properties [latex]\Delta G[/latex] and K.
[latex]E^\circ[/latex] and [latex]\Delta G^\circ[/latex]
The standard free energy change of a process, [latex]\Delta G^\circ[/latex], was defined in a previous chapter as the maximum work that could be performed by a system, [latex]w_{max}[/latex]. In the case of a redox reaction taking place within a galvanic cell under standard state conditions, essentially all the work is associated with transferring the electrons from reductant-to-oxidant, [latex]w_{elec}[/latex]:
[latex]\Delta G^\circ = w_{max} = w_{elec}[/latex]
The work associated with transferring electrons is determined by the total amount of charge (coulombs) transferred and the cell potential:
[latex]\Delta G^\circ = w_{elec} = -nFE_{cell}^\circ[/latex]
[latex]\Delta G^\circ = -nFE_{cell}^\circ[/latex]
where n is the number of moles of electrons transferred, F is Faraday’s constant, and [latex]E_{cell}^\circ[/latex] is the standard cell potential. The relation between free energy change and standard cell potential confirms the sign conventions and spontaneity criteria previously discussed for both of these properties: spontaneous redox reactions exhibit positive potentials and negative free energy changes.
[latex]E^\circ[/latex] and K
Combining a previously derived relation between [latex]\Delta G^\circ[/latex] and K (see the chapter on thermodynamics) and the equation above relating [latex]\Delta G^\circ[/latex] and [latex]E_{cell}^\circ[/latex] yields the following:
[latex]\Delta G^\circ = -RT\text{ln}K = -nFE_{cell}^\circ[/latex]
[latex]E_{cell}^\circ = (\dfrac{RT}{nF})\text{ln}K[/latex]
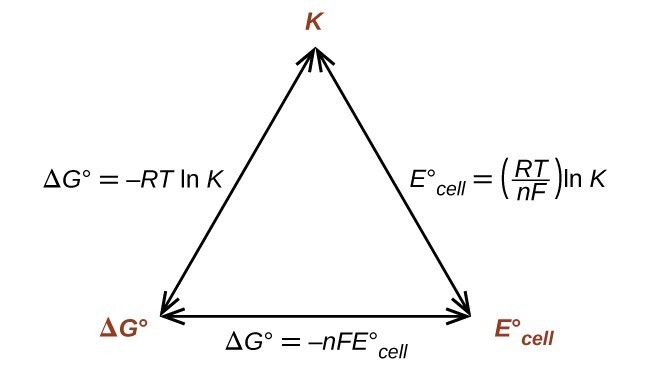
This equation indicates redox reactions with large (positive) standard cell potentials will proceed far towards completion, reaching equilibrium when the majority of reactant has been converted to product. A summary of the relations between [latex]E^\circ[/latex], [latex]\Delta G^\circ[/latex] and [latex]K[/latex] is depicted in Figure 17.4.1, and a table correlating reaction spontaneity to values of these properties is provided in Table 17.4.1.
Example 17.4.1: Equilibrium Constants, Standard Cell Potentials, and Standard Free Energy Changes
What is the standard free energy change and equilibrium constant for the following reaction at 25 °C?
[latex]\ce{Ag}(aq)+\ce{Fe}(s)\rightleftharpoons \ce{2Ag}(s)+\ce{Fe^2+}(aq)[/latex]
Show Solution
The reaction involves an oxidation-reduction reaction, so the standard cell potential can be calculated using the data in Standard Electrode (Half-Cell) Potentials.
[latex]\begin{array}{rll}\text{anode (oxidation):}&\ce{Fe}\left(s\right)\longrightarrow {\ce{Fe}}^{2+}\left(aq\right)+{\text{2e}}^{-}&{E}_{{\ce{Fe}}^{2+}\ce{/Fe}}^{\circ }=-\text{0.447 V}\\ \text{cathode (reduction):}&2\times \left({\ce{Ag}}^{\text{+}}\left(aq\right)+{\text{e}}^{-}\longrightarrow \ce{Ag}\left(s\right)\right)&{E}_{{\ce{Ag}}^{\text{+}}\ce{/Ag}}^{\circ }=\text{0.7996 V}\end{array}[/latex]
[latex]{E}_{\text{cell}}^{\circ }={E}_{\text{cathode}}^{\circ }-{E}_{\text{anode}}^{\circ }=\qquad{E}_{{\ce{Ag}}^{\text{+}}\ce{/Ag}}^{\circ }-{E}_{{\ce{Fe}}^{2+}\ce{/Fe}}^{\circ }=\text{+1.247 V}[/latex]
Remember that the cell potential for the cathode is not multiplied by two when determining the standard cell potential. With n = 2, the equilibrium constant is then
[latex]\begin{array}{rll}{E}_{\text{cell}}^{\circ }&=&\frac{\text{0.0592 V}}{n}\log{K}\\K&=&{10}^{n\times {E}_{\text{cell}}^{\circ }\text{/}\text{0.0592 V}}\\{}&=&{10}^{2\times \text{1.247 V/0.0592 V}}\\{}&=&{10}^{42.128}\\{}&=&1.3\times {10}^{42}\end{array}[/latex]
The two equilibrium constants differ slightly due to rounding in the constants 0.0257 V and 0.0592 V. The standard free energy is then
[latex]\Delta {G}^{\circ }=-nF{E}_{\text{cell}}^{\circ }[/latex]
[latex]\Delta G^{\circ }=-2\times\text{96,485}\frac{\text{J}}{\text{V}\cdot \text{mol}}\times \text{1.247 V}=-240.6\frac{\text{kJ}}{\text{mol}}[/latex]
The reaction is spontaneous, as indicated by a negative free energy change and a positive cell potential. The K value is very large, indicating the reaction proceeds to near completion to yield an equilibrium mixture containing mostly products.
Check Your Learning
Potentials at Nonstandard Conditions: The Nernst Equation
Most of the redox processes that interest science and society do not occur under standard state conditions, and so the potentials of these systems under nonstandard conditions are a property worthy of attention. Having established the relationship between potential and free energy change in this section, the previously discussed relation between free energy change and reaction mixture composition can be used for this purpose.
[latex]\Delta G = \Delta G^\circ + RT\text{ln}Q[/latex]
Notice the reaction quotient, [latex]Q[/latex], appears in this equation, making the free energy change dependent upon the composition of the reaction mixture. Substituting the equation relating free energy change to cell potential yields the Nernst equation:
[latex]-nFE_{cell} = -nFE_{cell}^\circ + RT\text{ln}Q[/latex]
[latex]E_{cell} = E_{cell}^\circ - \dfrac{RT}{nF}\text{ln}Q[/latex]
This equation describes how the potential of a redox system (such as a galvanic cell) varies from its standard state value, specifically, showing it to be a function of the number of electrons transferred, [latex]n[/latex] the temperature, [latex]T[/latex], and the reaction mixture composition as reflected in [latex]Q[/latex]. A convenient form of the Nernst equation for most work is one in which values for the fundamental constants (R and F) and a factor converting from natural to base-10 logarithms have been included.
[latex]E_{cell} = E_{cell}^\circ - \dfrac{0.0592 \text{V}}{n}\text{log}Q[/latex]
Example 17.4.2: Predicting Redox Spontaneity Under Nonstandard Conditions
Use the Nernst equation to predict the spontaneity of the redox reaction shown below.
[latex]\ce{Co}(s)+\ce{Fe^2+}(aq, \text{1.94}M)\longrightarrow \ce{Co^2+}(aq, \text{0.15}M)+\ce{Fe}(s)[/latex]
Show Solution
There are two ways to solve the problem. If the thermodynamic information in Standard Thermodynamic Properties for Selected Substances were available, you could calculate the free energy change. If the free energy change is negative, the process is spontaneous. The other approach, which we will use, requires information like that given in Standard Electrode (Half-Cell) Potentials. Using those data, the cell potential can be determined. If the cell potential is positive, the process is spontaneous. Collecting information from Standard Electrode (Half-Cell) Potentials and the problem,
[latex]\begin{array}{rll}\text{Anode (oxidation):}&\ce{Co}\left(s\right)\longrightarrow {\ce{Co}}^{2+}\left(aq\right)+{\text{2e}}^{-}&{E}_{{\ce{Co}}^{2+}\ce{/Co}}^{\circ }=-\text{0.28 V}\\ \text{Cathode (reduction):}&{\ce{Fe}}^{2+}\left(aq\right)+{\text{2e}}^{-}\longrightarrow \ce{Fe}\left(s\right)&{E}_{{\ce{Fe}}^{2+}\ce{/Fe}}^{\circ }=-\text{0.447 V}\end{array}[/latex]
[latex]{E}_{\text{cell}}^{\circ }={E}_{\text{cathode}}^{\circ }-{E}_{\text{anode}}^{\circ }=\qquad{-}\text{0.447 V}-\left(-\text{0.28 V}\right)=-\text{0.17 V}[/latex]
Notice the negative value of the standard cell potential indicates the process is not spontaneous under standard conditions. Substitution of the Nernst equation terms for the nonstandard conditions yields:
[latex]\begin{array}{rll}Q &=&\frac{\left[\ce{Co}^{2+}\right]}{\left[\ce{Fe}^{2+}\right]}=\dfrac{0.15M}{1.94M}=0.077\\{E}_{\text{cell}}&=&{E}_{\text{cell}}^{\circ }-\frac{0.0592 V}{n}\log{Q}\\{E}_{\text{cell}}&=&-0.1\text{7 V}-\frac{0.0592 V}{2}\log{0.077}\\{E}_{\text{cell}}&=&-\text{0.17 V}+0.033 V=-0.014 V\end{array}[/latex]
The cell potential remains negative (slightly) under the specified conditions, and so the reaction remains nonspontaneous.
Check Your Learning
A concentration cell is constructed by connecting two nearly identical half-cells, each based on the same half-reaction and using the same electrode, varying only in the concentration of one redox species. The potential of a concentration cell, therefore, is determined only by the difference in concentration of the chosen redox species. The example problem below illustrates the use of the Nernst equation in calculations involving concentration cells.
Example 17.4.3: Concentration Cells
What is the cell potential of the concentration cell described by
[latex]\ce{Zn}(s)\mid \ce{Zn^2+}(aq\text{, 0.10}M)\parallel \ce{Zn^2+}(aq, \text{0.50}M)\mid \ce{Zn}(s)[/latex]
Show Solution
From the information given:
[latex]\begin{array}{rll}\text{Anode:}&\ce{Zn}\left(s\right)\longrightarrow {\ce{Zn}}^{2+}\left(aq\text{, 0.10}M\right)+{\text{2e}}^{-}&{E}_{\text{anode}}^{\circ }=-\text{0.7618 V}\\ \text{Cathode:}&{\ce{Zn}}^{2+}\left(aq\text{, 0.50}M\right)+{\text{2e}}^{-}\longrightarrow \ce{Zn}\left(s\right)&{E}_{\text{cathode}}^{\circ }=-\text{0.7618 V}\\ \\ \text{Overall:}&{\ce{Zn}}^{2+}\left(aq\text{, 0.50}M\right)\longrightarrow {\ce{Zn}}^{2+}\left(aq\text{, 0.10}M\right)&{E}_{\text{cell}}^{\circ }=\text{0.000 V}\end{array}[/latex]
Substituting into the Nernst equation,
[latex]{E}_{\text{cell}}=\text{0.000 V}-\dfrac{\text{0.0592 V}}{2}\log\dfrac{0.10}{0.50}=+0.021 V[/latex]
The positive value for cell potential indicates the overall cell reaction (see above) is spontaneous. This spontaneous reaction is one in which the zinc ion concentration in the cathode falls (it is reduced to elemental zinc) while that in the anode rises (it is produced by oxidation of the zinc anode). A greater driving force for zinc reduction is present in the cathode, where the zinc(II) ion concentration is greater (Ecathode > Eanode).
Check Your Learning
Key Concepts and Summary
Potential is a thermodynamic quantity reflecting the intrinsic driving force of a redox process, and it is directly related to the free energy change and equilibrium constant for the process. For redox processes taking place in electrochemical cells, the maximum (electrical) work done by the system is easily computed from the cell potential and the reaction stoichiometry and is equal to the free energy change for the process. The equilibrium constant for a redox reaction is logarithmically related to the reaction’s cell potential, with larger (more positive) potentials indicating reactions with greater driving force that equilibrate when the reaction has proceeded far towards completion (large value of K). Finally, the potential of a redox process varies with the composition of the reaction mixture, being related to the reactions standard potential and the value of its reaction quotient, Q, as described by the Nernst equation.
Key Equations
- [latex]{E}_{\text{cell}}^{\circ }=\dfrac{RT}{nF}\ln{K}[/latex]
- [latex]{E}_{\text{cell}}^{\circ }=\dfrac{0.02\text{57 V}}{n}\ln{K}=\dfrac{0.0\text{592 V}}{n}\log{K}\left(\text{at 298.15}K\right)[/latex]
- [latex]{E}_{\text{cell}}={E}_{\text{cell}}^{\circ }-\dfrac{RT}{nF}\ln{Q}\text{(Nernst equation)}[/latex]
- [latex]{E}_{\text{cell}}={E}_{\text{cell}}^{\circ }-\dfrac{0.02\text{57 V}}{n}\ln{Q}={E}_{\text{cell}}^{\circ }-\dfrac{0.05\text{92 V}}{n}\log{Q}\left(\text{at 298.15}K\right)[/latex]
- [latex]\Delta{G}=-nF{E}_{\text{cell}}[/latex]
- [latex]\Delta {G}^{\circ }=-nF{E}_{\text{cell}}^{\circ }[/latex]
- [latex]{w}_{\text{ele}}={w}_{\text{max}}=-nF{E}_{\text{cell}}[/latex]
Try It
- For the standard cell potentials given here, determine the [latex]\Delta[/latex]G° for the cell in kJ.
- 0.000 V, n = 2
- +0.434 V, n = 2
- −2.439 V, n = 1
- For the [latex]\Delta[/latex]G° values given here, determine the standard cell potential for the cell.
- 12 kJ/mol, n = 3
- −45 kJ/mol, n = 1
- Determine the standard cell potential and the cell potential under the stated conditions for the electrochemical reactions described here. State whether each is spontaneous or nonspontaneous under each set of conditions at 298.15 K.
- [latex]\ce{Hg}(l)+\ce{S^2-}(aq\text{, 0.10}M)+\ce{2Ag+}(aq\text{, 0.25}M)\longrightarrow \ce{2Ag}(s)+\ce{HgS}(s)[/latex]
- The galvanic cell made from a half-cell consisting of an aluminum electrode in 0.015 M aluminum nitrate solution and a half-cell consisting of a nickel electrode in 0.25 M nickel(II) nitrate solution.
- The cell made of a half-cell in which 1.0 M aqueous bromine is oxidized to 0.11 M bromide ion and a half-cell in which aluminum ion at 0.023 M is reduced to aluminum metal. Assume the standard reduction potential for [latex]\ce{Br2}[/latex](l) is the same as that of [latex]\ce{Br2}[/latex](aq).
- Determine [latex]\Delta[/latex]G and [latex]\Delta[/latex]G° for each of the reactions in the previous problem.
- Use the data in Standard Electrode (Half-Cell) Potentials to determine the equilibrium constant for the following reactions. Assume 298.15 K if no temperature is given.
- [latex]\ce{AgCl}(s)\rightleftharpoons \ce{Ag+}(aq)+\ce{Cl-}(aq)[/latex]
- [latex]\ce{CdS}(s)\rightleftharpoons \ce{Cd^2+}(aq)+\ce{S^2-}(aq)\text{at 377 K}[/latex]
- [latex]\ce{Hg^2+}(aq)+\ce{4Br-}(aq)\rightleftharpoons \ce{[HgBr4]^2-}(aq)[/latex]
- [latex]\ce{H2O}(l)\rightleftharpoons \ce{H+}(aq)+\ce{OH-}(aq)\text{at 25}^\circ C[/latex]
Show Selected Solutions
- [latex]\Delta G^{\circ }=-nF{E}_{\text{cell}}^{\circ }[/latex]
- [latex]\Delta G^{\circ }=-nF{E}_{\text{cell}}^{\circ }=-\left(2\right)\left(96485\frac{\text{C}}{\text{V mol}}\right)\left(\text{0.000 V}\right)=\text{0 J/mol}=\text{0 kJ/mol}[/latex]
- [latex]\Delta G^{\circ }=-nF{E}_{\text{cell}}^{\circ }=-\left(2\right)\left(96485\frac{\text{C}}{\text{V mol}}\right)\left(\text{+0.434 V}\right)=-\text{83749 J/mol}=-\text{83.7 kJ/mol}[/latex]
- [latex]\Delta G^{\circ }=-nF{E}_{\text{cell}}^{\circ }=-\left(1\right)\left(96485\frac{\text{C}}{\text{V mol}}\right)\left(-\text{2.439 V}\right)=\text{+235327 J/mol}=\text{+235.3 kJ/mol}[/latex]
- All reactions are at 298.15 K and use [latex]{E}_{\text{cell}}={E}_{\text{cell}}^{\circ }-\frac{RT}{nF}\ln{Q}={E}_{\text{cell}}^{\circ }-\frac{0.0592}{n}\log{Q}:[/latex]
- [latex]\begin{array}{rl}\text{anode: Hg}&\left(l\right)+\text{S}^{2-}\left(aq\text{, 0.25}M\right)\longrightarrow \text{HgS}\left(s\right)+{2\text{e}}^{-}{E}_{\text{anode}}^{\circ}=-0.70\text{ V}\\ \text{cathode:}&2\times\left(\text{Ag}^{+}\left(aq\text{, 0.25}M\right)+{\text{e}}^{-}\longrightarrow \text{Ag}\left(s\right)\right){E}_{\text{cathode}}^{\circ}=\text{0.7996 V}\\ \\ \text{overall: Hg}&\left(l\right)+{\text{S}}^{2-}\left(aq\right)+{\text{2Ag}}^{\text{+}}\left(aq\right)\longrightarrow \text{2Ag}\left(s\right)+\text{HgS}\left(s\right)\end{array}[/latex]
[latex]{E}_{\text{cell}}^{\circ }={E}_{\text{cathode}}^{\circ }-{E}_{\text{anode}}^{\circ }=\text{0.7996 V}-\left(-\text{0.70 V}\right)=\text{1.50 V}\left(\text{spontaneous}\right)[/latex]
[latex]{E}_{\text{cell}}^{\circ }={E}_{\text{cell}}^{\circ }-\frac{\text{0.0592 V}}{2}\log\frac{1}{0.10\times {0.25}^{2}}=\text{1.43 V (spontaneous)}[/latex] - standard cell potential: 1.405 V, spontaneous; cell potential under stated conditions: 1.423 V, spontaneous
- Oxidation occurs at the anode and reduction at the cathode.
- [latex]\begin{array}{rl}\text{anode: Hg}&\left(l\right)+\text{S}^{2-}\left(aq\text{, 0.25}M\right)\longrightarrow \text{HgS}\left(s\right)+{2\text{e}}^{-}{E}_{\text{anode}}^{\circ}=-0.70\text{ V}\\ \text{cathode:}&2\times\left(\text{Ag}^{+}\left(aq\text{, 0.25}M\right)+{\text{e}}^{-}\longrightarrow \text{Ag}\left(s\right)\right){E}_{\text{cathode}}^{\circ}=\text{0.7996 V}\\ \\ \text{overall: Hg}&\left(l\right)+{\text{S}}^{2-}\left(aq\right)+{\text{2Ag}}^{\text{+}}\left(aq\right)\longrightarrow \text{2Ag}\left(s\right)+\text{HgS}\left(s\right)\end{array}[/latex]
- All use [latex]K={e}^{nF{E}_{\text{cell}}^{\circ }\text{/}RT}[/latex] with [latex]{E}_{\text{cell}}^{\circ }={E}_{\text{cathode}}^{\circ }-{E}_{\text{anode}}^{\circ }\text{:}[/latex]
- 1.7 × 10−10
- 2.6 × 10−21
- 8.9 × 1019
- 1.0 × 10−14
Glossary
concentration cell: galvanic cell in which the two half-cells are the same except for the concentration of the solutes; spontaneous when the overall reaction is the dilution of the solute
electrical work (wele): negative of total charge times the cell potential; equal to wmax for the system, and so equals the free energy change ([latex]\Delta[/latex]G)
Faraday’s constant (F): charge on 1 mol of electrons; F = 96,485 C/mol e−
Nernst equation: equation that relates the logarithm of the reaction quotient (Q) to nonstandard cell potentials; can be used to relate equilibrium constants to standard cell potentials
Licenses and Attributions (Click to expand)
CC licensed content, Shared previously
- Chemistry 2e. Provided by: OpenStax. Located at: https://openstax.org/. License: CC BY: Attribution. License Terms: Access for free at
https://openstax.org/books/chemistry-2e/pages/1-introduction
All rights reserved content
- Practice Problem: Cell Potential, Equilibrium Constants, and Free Energy Change. Authored by: Professor Dave Explains. Located at: https://youtu.be/cW7RpCYAOdI. License: Other. License Terms: Standard YouTube License
charge on 1 mol of electrons; F = 96,485 C/mol e−
equation that relates the logarithm of the reaction quotient (Q) to nonstandard cell potentials; can be used to relate equilibrium constants to standard cell potentials
galvanic cell in which the two half-cells are the same except for the concentration of the solutes; spontaneous when the overall reaction is the dilution of the solute

