"

Chapter 16: Equilibria of Other Reaction Classes

16.1 Precipitation and Dissolution

Learning Outcomes

  • Write chemical equations and equilibrium expressions representing solubility equilibria
  • Carry out equilibrium computations involving solubility, equilibrium expressions, and solute concentrations

Solubility equilibria are established when the dissolution and precipitation of a solute species occur at equal rates. These equilibria underlie many natural and technological processes, ranging from tooth decay to water purification. An understanding of the factors affecting compound solubility is, therefore, essential to the effective management of these processes. This section applies previously introduced chapter on equilibrium concepts and tools to systems involving dissolution and precipitation.

The Solubility Product

Recall from the chapter on solutions that the solubility of a substance can vary from essentially zero (insoluble or sparingly soluble) to infinity (miscible). A solute with finite solubility can yield a saturated solution when it is added to a solvent in an amount exceeding its solubility, resulting in a heterogeneous mixture of the saturated solution and the excess, undissolved solute. For example, a saturated solution of silver chloride (AgCl) is one in which the equilibrium shown below has been established.

[latex]\text{AgCl}\left(s\right){\underset{\text{precipitation}}{\overset{\text{dissolution}}{\rightleftharpoons}}}{\text{Ag}}^{+}\left(aq\right)+{\text{Cl}}^{-}\left(aq\right)[/latex]

In this solution, an excess of solid AgCl dissolves and dissociates to produce aqueous [latex]\ce{Ag+}[/latex] and [latex]\ce{Cl-}[/latex] ions at the same rate that these aqueous ions combine and precipitate to form solid [latex]\ce{AgCl}[/latex] (Figure 16.1.1). Because silver chloride is a sparingly soluble salt, the equilibrium concentration of its dissolved ions in the solution is relatively low.

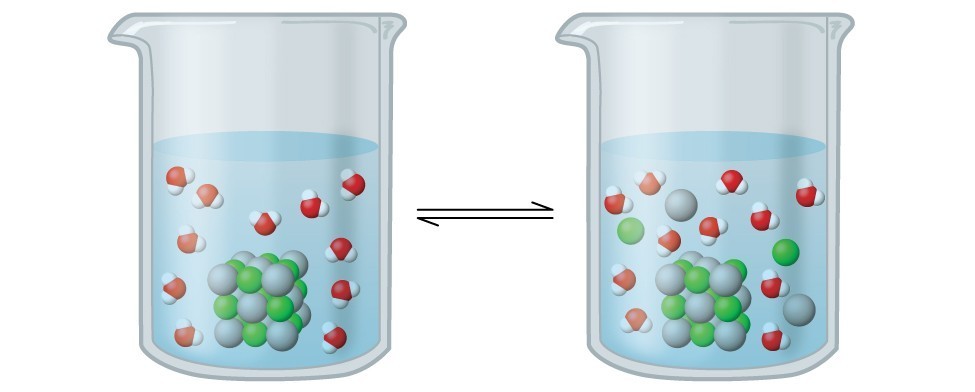
Two beakers are shown with a bidirectional arrow between them. Both beakers are just over half filled with a clear, colorless liquid. The beaker on the left shows a cubic structure composed of alternating green and slightly larger grey spheres. Evenly distributed in the region outside, 11 space filling models are shown. These are each composed of a central red sphere with two smaller white spheres attached in a bent arrangement. In the beaker on the right, the green and grey spheres are no longer connected in a cubic structure. Nine green spheres, 10 grey spheres, and 11 red and white molecules are evenly mixed and distributed throughout the liquid in the beaker.
Figure 16.1.1. Silver chloride is a sparingly soluble ionic solid. When it is added to water, it dissolves slightly and produces a mixture consisting of a very dilute solution of Ag+ and Cl– ions in equilibrium with undissolved silver chloride. (Ag = gray spheres; Cl = green spheres; H = white spheres; O = red spheres)

The equilibrium constant for the equilibrium between a slightly soluble ionic solid and a solution of its ions is called the solubility product (Ksp) of the solid. Recall from the chapter on solutions and colloids that we use an ion’s concentration as an approximation of its activity in a dilute solution. For silver chloride, at equilibrium:

[latex]\text{AgCl}\left(s\right)\rightleftharpoons {\text{Ag}}^{\text{+}}\left(aq\right)+{\text{Cl}}^{-}\left(aq\right)\qquad{K}_{\text{sp}}=\left[{\text{Ag}}^{\text{+}}\left(aq\right)\right]\left[{\text{Cl}}^{-}\left(aq\right)\right][/latex]

Recall that only gases and solutes are represented in equilibrium constant expressions, so the Ksp does not include a term for the undissolved [latex]\ce{AgCl}[/latex]. A listing of solubility product constants for several sparingly soluble compounds is provided in Solubility Products. Each of these equilibrium constants is much smaller than 1 because the compounds listed are only slightly soluble. A small Ksp represents a system in which the equilibrium lies to the left, so that relatively few hydrated ions would be present in a saturated solution.

Table 16.1.1. Common Solubility Products by Decreasing Equilibrium Constants
Substance Ksp at 25 °C
[latex]\ce{CuCl}[/latex] 1.2 × 10–6
[latex]\ce{CuBr}[/latex] 6.27 × 10–9
[latex]\ce{AgI}[/latex] 1.5 × 10–16
[latex]\ce{PbS}[/latex] 7 × 10–29
[latex]\ce{Al(OH)3}[/latex] 2 × 10–32
[latex]\ce{Fe(OH)3}[/latex] 4 × 10–38

Example 16.1.1: Writing Equations and Solubility Products

Write the dissolution equation and the solubility product expression for each of the following slightly soluble ionic compounds:

  1. [latex]\ce{AgI}[/latex], silver iodide, a solid with antiseptic properties
  2. [latex]\ce{CaCO3}[/latex], calcium carbonate, the active ingredient in many over-the-counter chewable antacids
  3. [latex]\ce{Mg(OH)2}[/latex], magnesium hydroxide, the active ingredient in Milk of Magnesia
  4. [latex]\ce{Mg(NH4)PO4}[/latex], magnesium ammonium phosphate, an essentially insoluble substance used in tests for magnesium
  5. [latex]\ce{Ca5(PO4)3OH}[/latex], the mineral apatite, a source of phosphate for fertilizers

(Hint: When determining how to break 4 and 5 up into ions, refer to the list of polyatomic ions in the section on chemical nomenclature.)

Show Solution
  1. [latex]\text{AgI}\left(s\right)\rightleftharpoons\text{Ag}^{+}\left(aq\right)+\text{I}^{-}\left(aq\right)\,\,\,\,\,\,\,{;}\,\,\,\,\,\,\,{K}_{\text{sp}}=\left[\text{Ag}^{+}\right]\left[\text{I}^{-}\right][/latex]
  2. [latex]\text{CaCO}_{3}\left(s\right)\rightleftharpoons\text{Ca}^{2+}\left(aq\right)+\text{CO}_{3}^{2-}\left(aq\right)\,\,\,\,\,\,\,{;}\,\,\,\,\,\,\,{K}_{\text{sp}}=\left[\text{Ca}^{2+}\right]\left[\text{CO}_{3}^{2-}\right][/latex]
  3. [latex]\text{Mg}\left(\text{OH}\right)_{2}\left(s\right)\rightleftharpoons\text{Mg}^{2+}\left(aq\right)+2\text{OH}^{-}\left(aq\right)\,\,\,\,\,\,\,{;}\,\,\,\,\,\,\,{K}_{\text{sp}}=\left[\text{Mg}^{2+}\right]\left[\text{OH}^{-}\right]^{2}[/latex]
  4. [latex]\text{Mg}\left(\text{NH}_{4}\right)\text{PO}_{4}\left(s\right)\rightleftharpoons\text{Mg}^{2+}\left(aq\right)+\text{NH}_{4}^{+}\left(aq\right)+\text{PO}_{4}^{3-}\left(aq\right) \,\,\,\,\,\,\,{;}\,\,\,\,\,\,\,{K}_{\text{sp}}=\left[\text{Mg}^{2+}\right]\left[\text{NH}_{4}^\text{+}\right]\left[\text{PO}_{4}^{3-}\right][/latex]
  5. [latex]\text{Ca}_{5}\left(\text{PO}_{4}\right)3\text{OH}\left(\text{s}\right)\rightleftharpoons5\text{Ca}^{2+}\left(aq\right)+3\text{PO}_{4}^{3-}\left(aq\right)+\text{OH}-\left(aq\right)\,\,\,\,\,\,\,{;}\,\,\,\,\,\,\,{K}_{\text{sp}}=\left[\text{Ca}^{2+}\right]^{5}\left[\text{PO}_{4}^{3-}\right]^{3}\left[\text{OH}^{-}\right][/latex]

Check Your Learning

Now we will extend the discussion of Ksp and show how the solubility product constant is determined from the solubility of its ions, as well as how Ksp can be used to determine the molar solubility of a substance.

Ksp and Solubility

The Ksp of a slightly soluble ionic compound may be simply related to its measured solubility provided the dissolution process involves only dissociation and solvation, for example:

[latex]{\text{M}}_{p}{\text{X}}_{q}\left(s\right)\rightleftharpoons p{\text{M}}^{\text{m+}}\left(aq\right)+q{\text{X}}^{\text{n}-}\left(aq\right)[/latex]

For cases such as these, one may derive Ksp values from provided solubilities, or vice-versa. Calculations of this sort are most conveniently performed using a compound’s molar solubility, measured as moles of dissolved solute per liter of saturated solution.

Example 16.1.2: Calculation of Ksp from Equilibrium Concentrations

Fluorite, [latex]\ce{CaF2}[/latex], is a slightly soluble solid that dissolves according to the equation:

[latex]{\text{CaF}}_{2}\left(s\right)\rightleftharpoons {\text{Ca}}^{\text{2+}}\left(aq\right)+{\text{2F}}^{-}\left(aq\right)[/latex]

The concentration of [latex]\ce{Ca^2+}[/latex] in a saturated solution of [latex]\ce{CaF2}[/latex] is 2.15 × 10–4M. What is the solubility product of fluorite?

Show Solution

According to the stoichiometry of the dissolution equation, the fluoride ion molarity of a [latex]\ce{CaF2}[/latex] solution is equal to twice its calcium ion molarity:

[latex][\text{F}^{-}]=(2\text{ mol F}^{-}/1\text{ mol Ca}^{2+})=(2)(2.15\times{10}^{-4}M)=4.30\times{10}^{-4}M[/latex]

Substituting the ion concentrations into the Ksp expression gives

[latex]{K}_{\text{sp}}={\text{[Ca}}^{\text{2+}}\text{]}\text{[}{\text{F}}^{-}{]}^{2}=\text{(2.15}\times {10}^{-4}\big){\left(4.30\times {10}^{-4}\right)}^{2}=\text{3.98}\times {10}^{-11}[/latex]

Check Your Learning

Example 16.1.3: Determination of Molar Solubility from Ksp

The Ksp of copper(I) bromide, [latex]\ce{CuBr}[/latex], is 6.3 × 10–9. Calculate the molar solubility of copper bromide.

Show Solution

The solubility product constant of copper(I) bromide is 6.3 × 10–9. The reaction is:

[latex]\text{CuBr}\left(s\right)\rightleftharpoons {\text{Cu}}^{\text{+}}\left(aq\right)+{\text{Br}}^{-}\left(aq\right)[/latex]

First, write out the solubility product equilibrium constant expression:

[latex]{K}_{\text{sp}}=\text{[}{\text{Cu}}^{\text{+}}{]\text{[}\text{Br}}^{-}\text{]}[/latex]

Create an ICE table (as introduced in the chapter on fundamental equilibrium concepts), leaving the [latex]\ce{CuBr}[/latex] column empty as it is a solid and does not contribute to the Ksp:

This table has two main columns and four rows. The first row for the first column does not have a heading and then has the following in the first column: Initial concentration ( M ), Change ( M ), and Equilibrium concentration ( M ). The second column has the header of, “C u B r equilibrium arrow C u superscript positive sign plus B r superscript negative sign.” Under the second column is a subgroup of three rows and three columns. The first column is blank. The second column has the following: 0, x, 0 plus x equals x. The third column has the following 0, x, 0 plus x equals x.

At equilibrium:

[latex]{K}_{\text{sp}}=\left[\text{Cu}^{+}\right]\left[\text{Br}^{-}\right][/latex]
[latex]6.3\times {10}^{-9}=\left(x\right)\left(x\right)={x}^{2}[/latex]
[latex]x=\sqrt{\left(6.3\times {10}^{-9}\right)}=\text{7.9}\times {10}^{-5}[/latex]

Therefore, the molar solubility of [latex]\ce{CuBr}[/latex] is 7.9 × 10–5M.

Check Your Learning

Example 16.1.4: Determination of Molar Solubility from Ksp, Part II

The Ksp of calcium hydroxide, [latex]\ce{Ca(OH)2}[/latex], is 1.3 × 10–6. Calculate the molar solubility of calcium hydroxide.

Show Solution

The dissolution equation and solubility product expression are

[latex]{\text{Ca(OH)}}_{2}\left(s\right)\rightleftharpoons {\text{Ca}}^{\text{2+}}\left(aq\right)+{\text{2OH}}^{-}\left(aq\right)[/latex]

[latex]{K}_{\text{sp}}=\left[\text{Ca}^{2+}\right]\left[\text{OH}^{-}\right]^{2}[/latex]

Create an ICE table, leaving the [latex]\ce{Ca(OH)2}[/latex] column empty as it is a solid and does not contribute to the Ksp:

This table has two main columns and four rows. The first row for the first column does not have a heading and then has the following in the first column: Initial concentration ( M ), Change ( M ), and Equilibrium concentration ( M ). The second column has the header of, “C a ( O H ) subscript 2 equilibrium arrow C a superscript 2 positive sign plus 2 O H superscript negative sign.” Under the second column is a subgroup of three rows and three columns. The first column is blank. The second column has the following: 0, positive x, x. The third column has the following 0, positive 2 x, 2 x.

At equilibrium:

[latex]{K}_{\text{sp}}=\left[\text{Ca}^{2+}\right]\left[\text{OH}^{-}\right]^{2}[/latex]
[latex]1.3\times{10}^{-6}=\left(x\right)\left(2x\right)^{2}=\left(x\right)\left(4x^{2}\right)=4{x}^{3}[/latex]
[latex]x=\sqrt[3]{\dfrac{1.3\times {10}^{-6}}{4}}=\text{6.9}\times {10}^{-3}[/latex]

Therefore, the molar solubility of [latex]\ce{Ca(OH)2}[/latex] is 6.9 × 10–3M.

Check Your Learning

Note that solubility is not always given as a molar value. When the solubility of a compound is given in some unit other than moles per liter, we must convert the solubility into moles per liter (i.e., molarity) in order to use it in the solubility product constant expression. Example 16.1.5 shows how to perform those unit conversions before determining the solubility product equilibrium.

Example 16.1.5: Determination of Ksp from Gram Solubility

Many of the pigments used by artists in oil-based paints (Figure 16.1.2) are sparingly soluble in water. For example, the solubility of the artist’s pigment chrome yellow, [latex]\ce{PbCrO4}[/latex], is 4.6 × 10–6 g/L. Determine the solubility product for [latex]\ce{PbCrO4}[/latex].

A photograph is shown of a portion of an oil painting which reveals colors of orange, brown, yellow, green, blue, and purple colors in its strokes. A few water droplets rest on the surface.
Figure 16.1.2. Oil paints contain pigments that are very slightly soluble in water. In addition to chrome yellow ([latex]\ce{PbCrO4}[/latex]), examples include Prussian blue ([latex]\ce{Fe7(CN)_{18}}[/latex]), the reddish-orange color vermilion ([latex]\ce{HgS}[/latex]), and green color veridian ([latex]\ce{Cr2O3}[/latex]). (credit: Sonny Abesamis)
Show Solution

We are given the solubility of [latex]\ce{PbCrO4}[/latex] in grams per liter. If we convert this solubility into moles per liter, we can find the equilibrium concentrations of Pb2+ and [latex]{\text{CrO}}_{4}^{2-}[/latex], then Ksp:This figure shows four horizontally oriented rectangles. The first three from the left are shaded green and the last one at the right is shaded white. Right pointing arrows between the rectangles are labeled “1,” “2,” and “3” moving left to right across the diagram. The first rectangle is labeled “Solubility of P b C r O subscript 4, in g divdided by L.” The second rectangle is labeled “[ P b C r O subscript 4 ], in m o l divided by L.” The third is labeled “[ P b superscript 2 plus] and [ C r O subscript 4 superscript 2 negative ].” The fourth rectangle is labeled “K subscript s p.”Step 1. Use the molar mass of [latex]\ce{PbCrO4}[/latex], [latex]\left(\dfrac{323.2\text{g}}{1\text{mol}}\right)[/latex], to convert the solubility of PbCrO4 in grams per liter into moles per liter:

[latex]\begin{array}{l}{ }\left[{\text{PbCrO}}_{4}\right]&=&\dfrac{4.6\times {10}^{-6}{\text{g PbCrO}}_{4}}{1\text{L}}\times \dfrac{1{\text{mol PbCrO}}_{4}}{323.2{\text{g PbCrO}}_{4}}\\& =&\dfrac{1.4\times {10}^{-8}{\text{mol PbCrO}}_{4}}{1\text{L}}\\& =&\text{}1.4\times {10}^{-8}M\end{array}[/latex]

Step 2. The chemical equation for the dissolution indicates that 1 mol of [latex]\ce{PbCrO4}[/latex] gives 1 mol of [latex]\ce{Pb^2+}[/latex](aq) and 1 mol of [latex]{\text{CrO}}_{4}{}^{\text{2-}}\text{(}aq\text{)}:[/latex]

[latex]{\text{PbCrO}}_{4}\left(s\right)\rightleftharpoons {\text{Pb}}^{2+}\left(aq\right)+{\text{CrO}}_{4}{}^{2-}\left(aq\right)[/latex]

The dissolution stoichiometry shows a 1:1 relation between the molar amounts of compound and its two ions, and so both [latex]\ce{[Pb^2+]}[/latex] and [latex]\left[{\text{CrO}}_{4}{}^{\text{2-}}\right][/latex] are equal to the molar solubility of [latex]\ce{PbCrO4}[/latex]

[latex]\left[\text{Pb}^{2+}\right]=\left[\text{CrO}_{4}^{2-}\right]=1.4\times{10}^{-8}M[/latex]

Step 3. Solve.

[latex]K_{\text{sp}}= [\text{Pb}^{2+}]\left[{\text{CrO}}_{4}{}^{2-}\right]=(1.4\times{10}^{-8})(1.4\times{10}^{-8}) = 2.0\times{10}^{-16}[/latex]

Check Your Learning

Example 16.1.6: Calculating the Solubility of [latex]\ce{Hg2Cl2}[/latex]

Calomel, [latex]\ce{Hg2Cl2}[/latex], is a compound composed of the diatomic ion of mercury(I), [latex]{\text{Hg}}_{2}{}^{\text{2+}}[/latex], and chloride ions, [latex]\ce{Cl-}[/latex]. Although most mercury compounds are now known to be poisonous, eighteenth-century physicians used calomel as a medication. Their patients rarely suffered any mercury poisoning from the treatments because calomel is quite insoluble:

[latex]{\text{Hg}}_{2}{\text{Cl}}_{2}\left(s\right)\rightleftharpoons {\text{Hg}}_{2}{}^{\text{2+}}\left(aq\right)+{\text{2Cl}}^{-}\left(aq\right)\qquad{K}_{\text{sp}}=\text{1.1}\times {10}^{-18}[/latex]

Calculate the molar solubility of [latex]\ce{Hg2Cl2}[/latex].

Show Solution

The molar solubility of [latex]\ce{Hg2Cl2}[/latex] is equal to the concentration of [latex]{\text{Hg}}_{2}{}^{\text{2+}}[/latex] ions because for each 1 mol of [latex]\ce{Hg2Cl2}[/latex] that dissolves, 1 mol of [latex]{\text{Hg}}_{2}{}^{\text{2+}}[/latex] forms:

This figure shows four horizontally oriented light green rectangles. Right pointing arrows are placed between them. The first rectangle is labeled “Determine the direction of change.” The second rectangle is labeled “Determine x and the equilibrium concentrations.” The third is labeled “Solve for x and the equilibrium concentrations.” The fourth rectangle is labeled “Check the math.”

  1. Determine the direction of change. Before any [latex]\ce{Hg2Cl2}[/latex] dissolves, Q is zero, and the reaction will shift to the right to reach equilibrium.
  2. Determine x and equilibrium concentrations. Concentrations and changes are given in the following ICE table:This table has two main columns and four rows. The first row for the first column does not have a heading and then has the following in the first column: Initial concentration ( M ), Change ( M ), Equilibrium concentration ( M ). The second column has the header of, “H g subscript 2 C l subscript 2 equilibrium arrow H g subscript 2 superscript 2 positive sign plus 2 C l superscript negative sign.” Under the second column is a subgroup of three rows and three columns. The first column is blank. The second column has the following: 0, x, 0 plus x equals x. The third column has the following: 0, 2 x, 0 plus 2 x equals 2 x.
  3. Note that the change in the concentration of [latex]\ce{Cl-}[/latex] (2x) is twice as large as the change in the concentration of [latex]{\text{Hg}}_{2}{}^{\text{2+}}[/latex] (x) because 2 mol of Cl– forms for each 1 mol of [latex]{\text{Hg}}_{2}{}^{\text{2+}}[/latex] that forms. [latex]\ce{Hg2Cl2}[/latex] is a pure solid, so it does not appear in the calculation.
  4. Solve for x and the equilibrium concentrations. We substitute the equilibrium concentrations into the expression for Ksp and calculate the value of x: [latex]{K}_{\text{sp}}=\left[\text{Hg}_{2}^{2+}\right]\left[\text{Cl}^{-}\right]^{2}[/latex][latex]1.1\times{10}^{-18}=\left(x\right)\left(2x\right)^{2}[/latex][latex]4{x}^{3}=\text{1.1}\times {10}^{-18}[/latex][latex]x=\sqrt[3]{\left(\frac{1.1\times {10}^{-18}}{4}\right)}=\text{6.5}\times {10}^{-7}\text{}M[/latex][latex]\left[{\text{Hg}}_{2}{}^{\text{2+}}\right]=\text{6.5}\times {10}^{-7}\text{}M=\text{6.5}\times {10}^{-7}\text{}M[/latex][latex]\left[\text{Cl}^{-}\right]=2x=2\left(6.5\times{10}^{-7}\right)=1.3\times {10}^{-6}M[/latex]The molar solubility of [latex]\ce{Hg2Cl2}[/latex] is equal to [latex]{\text{[Hg}}_{2}{}^{\text{2+}}][/latex], or 6.5 × 10–7M.
  5. Check the work. At equilibrium, Q = Ksp:
    [latex]Q=\left[\text{Hg}_{2}^{2+}\right]\left[\text{Cl}^{-}\right]^{2}=\left(6.5\times{10}^{-7}\right)\left(1.3\times{10}^{-6}\right)^{2}=1.1\times{10}^{-18}[/latex]
    The calculations check.

Check Your Learning

Tabulated Ksp values can also be compared to reaction quotients calculated from experimental data to tell whether a solid will precipitate in a reaction under specific conditions: Q equals Ksp at equilibrium; if Q is less than Ksp, the solid will dissolve until Q equals Ksp; if Q is greater than Ksp, precipitation will occur at a given temperature until Q equals Ksp.

Predicting Precipitation

The equation that describes the equilibrium between solid calcium carbonate and its solvated ions is:

[latex]{\text{CaCO}}_{3}\left(s\right)\rightleftharpoons {\text{Ca}}^{\text{2+}}\left(aq\right)+{\text{CO}}_{3}^{2-}\left(aq\right)\qquad{K}_{sp} = [\text{Ca}^{2+}][\text{CO}_3^{2-}] = 8.7 \times{10}^{-9}[/latex]

It is important to realize that this equilibrium is established in any aqueous solution containing [latex]\ce{Ca^2+}[/latex] and [latex]\ce{CO3^2-}[/latex] ions, not just in a solution formed by saturating water with calcium carbonate. Consider, for example, mixing aqueous solutions of the soluble compounds sodium carbonate and calcium nitrate. If the concentrations of calcium and carbonate ions in the mixture do not yield a reaction quotient, Qsp, that exceeds the solubility product, Ksp, then no precipitation will occur. If the ion concentrations yield a reaction quotient greater than the solubility product, then precipitation will occur, lowering those concentrations until equilibrium is established (Qsp = Ksp). The comparison of Qsp to Ksp to predict precipitation is an example of the general approach to predicting the direction of a reaction first introduced in the chapter on equilibrium. For the specific case of solubility equilibria:

Qsp < Ksp: the reaction proceeds in the forward direction (solution is not saturated; no precipitation observed)

Qsp > Ksp: the reaction proceeds in the reverse direction (solution is supersaturated; precipitation will occur)

This predictive strategy and related calculations are demonstrated in the next few example exercises.

Example 16.1.7: Precipitation of [latex]\ce{Mg(OH)2}[/latex]

The first step in the preparation of magnesium metal is the precipitation of [latex]\ce{Mg(OH)2}[/latex] from sea water by the addition of lime, [latex]\ce{Ca(OH)2}[/latex], a readily available inexpensive source of [latex]\ce{OH-}[/latex] ion:

[latex]{\text{Mg(OH)}}_{2}\left(s\right)\rightleftharpoons {\text{Mg}}^{\text{2+}}\left(aq\right)+{\text{2OH}}^{-}\left(aq\right)\,\,\,\,\,\,\,{;}\,\,\,\,\,\,\,{K}_{\text{sp}}=\text{2.1}\times {10}^{-13}[/latex]

The concentration of Mg2+(aq) in sea water is 0.0537 M. Will Mg(OH)2 precipitate when enough [latex]\ce{Ca(OH)2}[/latex] is added to give a [latex]\ce{[OH-]}[/latex] of 0.0010 M?

Show Solution

This problem asks whether the reaction:

[latex]{\text{Mg(OH)}}_{2}\left(s\right)\rightleftharpoons {\text{Mg}}^{\text{2+}}\left(aq\right)+{\text{2OH}}^{-}\left(aq\right)[/latex]

shifts to the left and forms solid [latex]\ce{Mg(OH)2}[/latex] when [latex]\ce{[Mg^2+]}[/latex] = 0.0537 M and [latex]\ce{[OH-]}[/latex] = 0.0010 M. The reaction shifts to the left if Q is greater than Ksp. Calculation of the reaction quotient under these conditions is shown here:

[latex]Q=\left[\text{Mg}^{2+}\right]\left[\text{OH}^{-}\right]^{2}=\left(0.0537\right)\left(0.0010\right)^{2}=5.4\times{10}^{-8}[/latex]

Because Q is greater than Ksp (Q = 5.4 × 10–8 is larger than Ksp = 2.1 × 10–13), we can expect the reaction to shift to the left and form solid magnesium hydroxide. [latex]\ce{Mg(OH)2}[/latex](s) forms until the concentrations of magnesium ion and hydroxide ion are reduced sufficiently so that the value of Q is equal to Ksp.

Check Your Learning

Example 16.1.8: Precipitation of AgCl upon Mixing Solutions

Does silver chloride precipitate when equal volumes of a 2.0 × 10–4–M solution of [latex]\ce{AgNO3}[/latex] and a 2.0 × 10–4–M solution of [latex]\ce{NaCl}[/latex] are mixed?

(Note: The solution also contains Na+ and [latex]{\text{NO}}_{3}^{-}[/latex] ions, but when referring to solubility rules, one can see that sodium nitrate is very soluble and cannot form a precipitate.)

Show Solution

The equation for the equilibrium between solid silver chloride, silver ion, and chloride ion is:

[latex]\text{AgCl}\left(s\right)\rightleftharpoons {\text{Ag}}^{\text{+}}\left(aq\right)+{\text{Cl}}^{-}\left(aq\right)[/latex]

The solubility product is 1.6 × 10–10 (see Solubility Products).

[latex]\ce{AgCl}[/latex] will precipitate if the reaction quotient calculated from the concentrations in the mixture of [latex]\ce{AgNO3}[/latex] and [latex]\ce{NaCl}[/latex] is greater than Ksp. The volume doubles when we mix equal volumes of [latex]\ce{AgNO3}[/latex] and [latex]\ce{NaCl}[/latex] solutions, so each concentration is reduced to half its initial value. Consequently, immediately upon mixing, [latex]\ce{[Ag+]}[/latex] and [latex]\ce{[Cl-]}[/latex] are both equal to:

[latex]\frac{1}{2}\left(2.0\times {10}^{-4}\right)\text{}M=\text{1.0}\times {10}^{-4}\text{}M[/latex].

The reaction quotient, Q, is momentarily greater than Ksp for [latex]\ce{AgCl}[/latex], so a supersaturated solution is formed:

[latex]Q=\left[\text{Ag}^{+}\right]\left[\text{Cl}^{-}\right]=\left(1.0\times{10}^{-4}\right)\left(1.0\times {10}^{-4}\right)=1.0\times{10}^{-8}\gt{K}_{\text{sp}}[/latex]

Since supersaturated solutions are unstable, [latex]\ce{AgCl}[/latex] will precipitate from the mixture until the solution returns to equilibrium, with Q equal to Ksp.

Check Your Learning

In the previous two examples, we have seen that Mg(OH)2 or [latex]\ce{AgCl}[/latex] precipitate when Q is greater than Ksp. In general, when a solution of a soluble salt of the Mm+ ion is mixed with a solution of a soluble salt of the Xn– ion, the solid, MpXq precipitates if the value of Q for the mixture of Mm+ and Xn– is greater than Ksp for MpXq. Thus, if we know the concentration of one of the ions of a slightly soluble ionic solid and the value for the solubility product of the solid, then we can calculate the concentration that the other ion must exceed for precipitation to begin. To simplify the calculation, we will assume that precipitation begins when the reaction quotient becomes equal to the solubility product constant.

Example 16.1.9: Precipitation of Calcium Oxalate

Blood will not clot if calcium ions are removed from its plasma. Some blood collection tubes contain salts of the oxalate ion, [latex]{\text{C}}_{2}{\text{O}}_{4}^{2-}[/latex], for this purpose (Figure 16.1.4). At sufficiently high concentrations, the calcium and oxalate ions form solid, [latex]\ce{CaC2O2·H2O}[/latex] (which also contains water bound in the solid). The concentration of [latex]\ce{Ca^2+}[/latex] in a sample of blood serum is 2.2 × 10–3M. What concentration of [latex]{\text{C}}_{2}{\text{O}}_{4}^{2-}[/latex] ion must be established before [latex]\ce{CaC2O4·H2O}[/latex] begins to precipitate?

A photograph is shown of 6 vials of blood resting on and near a black and white document. Two of the vials have purple caps, three have tan caps, and one has a red cap. Each has a label and the vials with tan caps have a small amount of an off-white material present in a layer at the base of the vial.
Figure 16.1.4. Anticoagulants can be added to blood that will combine with the [latex]\ce{Ca^2+}[/latex] ions in blood serum and prevent the blood from clotting. (credit: modification of work by Neeta Lind)
Show Solution

The equilibrium expression is:

[latex]{\text{CaC}}_{2}{\text{O}}_{4}\left(s\right)\rightleftharpoons {\text{Ca}}^{\text{2+}}\left(aq\right)+{\text{C}}_{2}{\text{O}}_{4}{}^{2-}\left(aq\right)[/latex]

For this reaction:

[latex]{K}_{\text{sp}}=\left[{\text{Ca}}^{\text{2+}}\right]\left[{\text{C}}_{2}{\text{O}}_{4}^{2-}\right]=1.96\times {10}^{-8}[/latex] (see Solubility Products)

[latex]\ce{CaC2O4}[/latex] does not appear in this expression because it is a solid. Water does not appear because it is the solvent.

Solid [latex]\ce{CaC2O4}[/latex] does not begin to form until Q equals Ksp. Because we know Ksp and [latex]\ce{[Ca^2+]}[/latex], we can solve for the concentration of [latex]{\text{C}}_{2}{\text{O}}_{4}^{2-}[/latex] that is necessary to produce the first trace of solid:

[latex]Q={K}_{\text{sp}}=\left[\text{Ca}^{2+}\right]\left[\text{C}_{2}\text{O}_{4}^{2-}\right]=1.96\times{10}^{-8}[/latex]

[latex]\left(2.2\times {10}^{-3}\right){\text{[C}}_{2}{\text{O}}_{4}{}^{\text{2-}}]=\text{1.96}\times {10}^{-8}[/latex]

[latex]\left[{\text{C}}_{2}{\text{O}}_{4}{}^{2-}\right]=\dfrac{1.96\times {10}^{-8}}{2.2\times {10}^{-3}}=8.9\times {10}^{-6}[/latex]

A concentration of [latex]\left[{\text{C}}_{2}{\text{O}}_{4}^{2-}\right][/latex] = 8.9 × 10–6M is necessary to initiate the precipitation of CaC2O4 under these conditions.

Check Your Learning

It is sometimes useful to know the concentration of an ion that remains in solution after precipitation. We can use the solubility product for this calculation too: If we know the value of Ksp and the concentration of one ion in solution, we can calculate the concentration of the second ion remaining in solution. The calculation is of the same type as that in Example 16.1.9—calculation of the concentration of a species in an equilibrium mixture from the concentrations of the other species and the equilibrium constant. However, the concentrations are different; we are calculating concentrations after precipitation is complete, rather than at the start of precipitation.

Example 16.1.10: Concentrations Following Precipitation

Clothing washed in water that has a manganese [[latex]\ce{Mn^2+}[/latex](aq)] concentration exceeding 0.1 mg/L (1.8 × 10–6M) may be stained by the manganese upon oxidation, but the amount of Mn2+ in the water can be reduced by adding a base. If a person doing laundry wishes to add a buffer to keep the pH high enough to precipitate the manganese as the hydroxide, [latex]\ce{Mn(OH)2}[/latex], what pH is required to keep [latex]\ce{[Mn^2+]}[/latex] equal to 1.8 × 10–6M?

Show Solution

The dissolution of [latex]\ce{Mn(OH)2}[/latex] is described by the equation:

[latex]{\text{Mn(OH)}}_{2}\left(s\right)\rightleftharpoons {\text{Mn}}^{\text{2+}}\left(aq\right)+{\text{2OH}}^{-}\left(aq\right)\,\,\,\,\,\,\,{;}\,\,\,\,\,\,\,{K}_{\text{sp}}=\text{2}\times {10}^{-13}[/latex]

We need to calculate the concentration of [latex]\ce{OH-}[/latex] when the concentration of [latex]\ce{Mn^2+}[/latex] is 1.8 × 10–6M. From that, we calculate the pH. At equilibrium:

[latex]{K}_{\text{sp}}=\left[\text{Mn}^{2+}\right]\left[\text{OH}^{-}\right]^{2}\qquad\text{ or }\qquad\left(1.8\times {10}^{-6}\right){\left[{\text{OH}}^{-}\right]}^{2}=\text{2}\times {10}^{-13}[/latex]

so

[latex]\left[{\text{OH}}^{-}\right]=\text{3.3}\times {10}^{-4}M[/latex].

Now we calculate the pH from the pOH:

[latex]\begin{array}{c}\text{pOH}=-\text{log}\left[{\text{OH}}^{-}\right]=-\text{log}\left(3.3\times {10}^{- 4}\right)=\text{3.48}\\ \text{pH}=\text{14.00}-\text{pOH}=\text{14.00}-\text{3.48}=\text{10.52}\end{array}[/latex]

(final result rounded to one significant digit, limited by the certainty of the Ksp)

Check Your Learning

In solutions containing two or more ions that may form insoluble compounds with the same counter ion, an experimental strategy called selective precipitation may be used to remove individual ions from solution. By increasing the counter ion concentration in a controlled manner, ions in solution may be precipitated individually, assuming their compound solubilities are adequately different. In solutions with equal concentrations of target ions, the ion forming the least soluble compound will precipitate first (at the lowest concentration of counter ion), with the other ions subsequently precipitating as their compound’s solubilities are reached. As an illustration of this technique, the next example exercise describes separation of a two halide ions via precipitation of one as a silver salt.

Example 16.1.11: Precipitation of Silver Halides

A solution contains 0.00010 mol of [latex]\ce{KBr}[/latex] and 0.10 mol of [latex]\ce{KCl}[/latex] per liter. [latex]\ce{AgNO3}[/latex] is gradually added to this solution. Which forms first, solid [latex]\ce{AgBr}[/latex] or solid [latex]\ce{AgCl}[/latex]?

Show Solution

The two equilibria involved are:

[latex]\text{AgCl}\left(s\right)\rightleftharpoons {\text{Ag}}^{\text{+}}\left(aq\right)+{\text{Cl}}^{-}\left(aq\right)\,\,\,\,\,\,\,{;}\,\,\,\,\,\,\,{K}_{\text{sp}}=\text{1.6}\times {10}^{-10}[/latex]
[latex]\text{AgBr}\left(s\right)\rightleftharpoons {\text{Ag}}^{\text{+}}\left(aq\right)+{\text{Br}}^{-}\left(aq\right)\,\,\,\,\,\,\,{;}\,\,\,\,\,\,\,K_{\text{sp}}=\text{5.0}\times {10}^{-13}[/latex]

If the solution contained about equal concentrations of [latex]\ce{Cl-}[/latex] and [latex]\ce{Br-}[/latex], then the silver salt with the smallest Ksp ([latex]\ce{AgBr}[/latex]) would precipitate first. The concentrations are not equal, however, so we should find the [latex]\ce{[Ag+]}[/latex] at which [latex]\ce{AgCl}[/latex] begins to precipitate and the [latex]\ce{[Ag+]}[/latex] at which [latex]\ce{AgBr}[/latex] begins to precipitate. The salt that forms at the lower [latex]\ce{[Ag+]}[/latex] precipitates first.

[latex]\ce{AgBr}[/latex] precipitates when Q equals Ksp for [latex]\ce{AgBr}[/latex]

[latex]Q=K_{\text{sp}}=\left[\text{Ag}^{+}\right]\left[\text{Br}^{-}\right]=\left[\text{Ag}^{+}\right]\left(0.00010\right)=5.0\times {10}^{-13}[/latex]
[latex][{\text{Ag}}^{\text{+}}\text{]}=\dfrac{\text{5.0}\times {10}^{-13}}{0.00010}=\text{5.0}\times {10}^{-9}[/latex]

[latex]\ce{AgBr}[/latex] begins to precipitate when [Ag+] is 5.0 × 10–9M.

For [latex]\ce{AgCl}[/latex]: [latex]\ce{AgCl}[/latex] precipitates when Q equals Ksp for [latex]\ce{AgCl}[/latex] (1.6 × 10–10). When [latex]\ce{[Cl-]}[/latex] = 0.10 M:

[latex]{Q}_{\text{sp}}=K_{\text{sp}}=\left[\text{Ag}^{+}\right]\left[\text{Cl}^{-}\right]=\left[\text{Ag}^{+}\right]\left(0.10\right)=1.6\times{10}^{-10}[/latex]
[latex][{\text{Ag}}^{\text{+}}\text{]}=\dfrac{1.6\times {10}^{-10}}{0.10}\text{=1.6}\times {10}^{-9}M[/latex]

[latex]\ce{AgCl}[/latex] begins to precipitate when [latex]\ce{[Ag+]}[/latex] is 1.6 × 10–9M.

[latex]\ce{AgCl}[/latex] begins to precipitate at a lower [latex]\ce{[Ag+]}[/latex] than [latex]\ce{AgBr}[/latex], so [latex]\ce{AgCl}[/latex] begins to precipitate first. Note the chloride ion concentration of the initial mixture was significantly greater than the bromide ion concentration, and so silver chloride precipitated first despite having a Ksp greater than that of silver bromide.

Check Your Learning

Common Ion Effect

Compared with pure water, the solubility of an ionic compound is less in aqueous solutions containing a common ion (one also produced by dissolution of the ionic compound). This is an example of a phenomenon known as the common ion effect, which is a consequence of the law of mass action that may be explained using Le ChÂtelier’s principle. Consider the dissolution of silver iodide:

[latex]\text{AgI}\left(s\right)\rightleftharpoons {\text{Ag}}^{\text{+}}\left(aq\right)+{\text{I}}^{-}\left(aq\right)[/latex]

This solubility equilibrium may be shifted left by the addition of either silver(I) or iodide ions, resulting in the precipitation of AgI and lowered concentrations of dissolved [latex]\ce{Ag+}[/latex] and [latex]\ce{I-}[/latex]. In solutions that already contain either of these ions, less [latex]\ce{AgI}[/latex] may be dissolved than in solutions without these ions.

This effect may also be explained in terms of mass action as represented in the solubility product expression:

[latex]K_{sp} = [\text{Ag}^+][\text{I}^-][/latex]

The mathematical product of silver(I) and iodide ion molarities is constant in an equilibrium mixture regardless of the source of the ions, and so an increase in one ion’s concentration must be balanced by a proportional decrease in the other.

Example 16.1.12: Common Ion Effect on Solubility

What is the effect on the amount of solid [latex]\ce{Mg(OH)2}[/latex] and the concentrations of [latex]\ce{Mg^2+}[/latex] and [latex]\ce{OH-}[/latex] when each of the following are added to a saturated solution of [latex]\ce{Mg(OH)2}[/latex]?

  1. [latex]\ce{MgCl2}[/latex]
  2. [latex]\ce{KOH}[/latex]
  3. [latex]\ce{NaNO3}[/latex]
  4. [latex]\ce{Mg(OH)2}[/latex]
Show Solution

The solubility equilibrium is

[latex]\text{Mg(OH)}_2(s) \rightleftharpoons \text{Mg}^{2+} (aq) + 2\text{OH}^- (aq)[/latex]

  1. Adding a common ion, [latex]\ce{Mg^2+}[/latex], will increase the concentration of this ion and shift the solubility equilibrium to the left, decreasing the concentration of hydroxide ion and increasing the amount of undissolved magnesium hydroxide.
  2. Adding a common ion, [latex]\ce{OH-}[/latex], will increase the concentration of this ion and shift the solubility equilibrium to the left, decreasing the concentration of magnesium ion and increasing the amount of undissolved magnesium hydroxide.
  3. The added compound does not contain a common ion, and no effect on the magnesium hydroxide solubility equilibrium is expected.
  4. Adding more solid magnesium hydroxide will increase the amount of undissolved compound in the mixture. The solution is already saturated, though, so the concentrations of dissolved magnesium and hydroxide ions will remain the same.
  5. [latex]Q = [\text{Mg}^{2+}][\text{OH}^-]^2[/latex]
  6. Thus, changing the amount of solid magnesium hydroxide in the mixture has no effect on the value of Q, and no shift is required to restore Q to the value of the equilibrium constant.

Check Your Learning

Key Concepts and Summary

The equilibrium constant for an equilibrium involving the precipitation or dissolution of a slightly soluble ionic solid is called the solubility product, Ksp, of the solid. When we have a heterogeneous equilibrium involving the slightly soluble solid MpXq and its ions Mm+ and Xn–:

[latex]\text{M}_{\text{p}}{\text{X}}_{\text{q}}\left(s\right)\rightleftharpoons p{\text{M}}^{\text{m+}}\left(aq\right)+q{\text{X}}^{\text{n}-}\left(aq\right)[/latex]

We write the solubility product expression as:

[latex]{K}_{\text{sp}}={{\text{[M}}^{\text{m+}}\text{]}}^{\text{p}}{{\text{[X}}^{\text{n}-}]}^{\text{q}}[/latex]

The solubility product of a slightly soluble electrolyte can be calculated from its solubility; conversely, its solubility can be calculated from its Ksp, provided the only significant reaction that occurs when the solid dissolves is the formation of its ions.

A slightly soluble electrolyte begins to precipitate when the magnitude of the reaction quotient for the dissolution reaction exceeds the magnitude of the solubility product. Precipitation continues until the reaction quotient equals the solubility product.

Key Equations

  • [latex]\text{Mp}_{\text{Xq}}\left(s\right)\rightleftharpoons p{\text{M}}^{\text{m+}}\left(aq\right)+q{\text{X}}^{\text{n}-}\left(aq\right)\,\,\,\,\,\,\,{;}\,\,\,\,\,\,\,{K}_{\text{sp}}=\left[\text{M}^{\text{m+}}\right]^{\text{p}}\left[\text{X}^{\text{n}-}\right]^\text{q}[/latex]

Try It

  1. Complete the changes in concentrations for each of the following reactions:
    1. [latex]\begin{array}{ccc}\text{AgI}\left(s\right)\longrightarrow & {\text{Ag}}^{\text{+}}\left(aq\right)& +{\text{I}}^{-}\left(aq\right)\\ & x&\text{ _____}\end{array}[/latex]
    2. [latex]\begin{array}{ccc}{\text{CaCO}}_{3}\left(s\right)\longrightarrow & {\text{Ca}}^{\text{2+}}\left(aq\right)+& {\text{CO}}_{3}{}^{2-}\left(aq\right)\\ & \text{____}& x\end{array}[/latex]
    3. [latex]\begin{array}{ccc}\text{Mg}{\left(\text{OH}\right)}_{2}\left(s\right)\longrightarrow & {\text{Mg}}^{\text{2+}}\left(aq\right)+& 2{\text{OH}}^{-}\left(aq\right)\\ & x&\text{ _____}\end{array}[/latex]
    4. [latex]\begin{array}{ccc}{\text{Mg}}_{3}{\left({\text{PO}}_{4}\right)}_{2}\left(s\right)\longrightarrow & 3{\text{Mg}}^{\text{2+}}\left(aq\right)+& 2{\text{PO}}_{4}{}^{3-}\left(aq\right)\\ & & x\text{_____}\end{array}[/latex]
    5. [latex]\begin{array}{cccc}{\text{Ca}}_{5}{\left({\text{PO}}_{4}\right)}_{3}\text{OH}\left(s\right)\longrightarrow & 5{\text{Ca}}^{\text{2+}}\left(aq\right)+& 3{\text{PO}}_{4}^{3-}\left(aq\right)+& {\text{OH}}^{-}\left(aq\right)\\ & \text{_____}& \text{_____}& x\end{array}[/latex]
  2. How do the concentrations of [latex]\ce{Ag+}[/latex] and [latex]{\text{CrO}}_{4}^{2-}[/latex] in a saturated solution above 1.0 g of solid [latex]\ce{Ag2CrO4}[/latex] change when 100 g of solid [latex]\ce{Ag2CrO4}[/latex] is added to the system? Explain.
  3. Assuming that no equilibria other than dissolution are involved, calculate the concentrations of ions in a saturated solution of each of the following (see Solubility Products):
    1. [latex]\ce{AgI}[/latex]
    2. [latex]\ce{Ag2SO4}[/latex]
    3. [latex]\ce{Mn(OH)2}[/latex]
    4. [latex]\ce{Sr(OH)2·8H2O}[/latex]
    5. the mineral brucite, [latex]\ce{Mg(OH)2}[/latex]
Show Selected Solutions
  1. In dissolution, one unit of substance produces a quantity of discrete ions or polyatomic ions that equals the number of times that the subunit appears in the formula.
    1. [latex]\begin{array}{ccc}\text{AgI}\left(s\right)\rightleftharpoons & {\text{Ag}}^{\text{+}}\left(aq\right)+& {\text{I}}^{-}\left(aq\right)\\ & x& {x}\end{array}[/latex]
      Dissolving AgI(s) must produce the same amount of I– ion as it does Ag+ ion.
    2. [latex]\begin{array}{ccc}{\text{CaCO}}_{3}\left(s\right)\rightleftharpoons & {\text{Ca}}^{\text{2+}}\left(aq\right)+& {\text{CO}}_{3}^{2-}\left(aq\right)\\ & {x}& x\end{array}[/latex]
      Dissolving [latex]\ce{CaCO3}[/latex](s) must produce the same amount of [latex]\ce{Ca^2+}[/latex] ion as it does [latex]{\text{CO}}_{3}^{2-}[/latex] ion.
    3. [latex]\begin{array}{lll}\text{Mg}{\left(\text{OH}\right)}_{2}\left(s\right)\longrightarrow \hfill & {\text{Mg}}^{\text{2+}}\left(aq\right)\hfill & +2{\text{OH}}^{-}\left(aq\right)\hfill \\ \hfill & x\hfill & {\text{2}x}\hfill \end{array}[/latex]
      When one unit of [latex]\ce{Mg(OH)2}[/latex] dissolves, two ions of [latex]\ce{OH-}[/latex] are formed for each [latex]\ce{Mg^2+}[/latex] ion.
    4. [latex]\begin{array}{ccc}{\text{Mg}}_{3}{\left({\text{PO}}_{4}\right)}_{2}\left(s\right)\rightleftharpoons & {\text{3Mg}}^{\text{2+}}\left(aq\right)+& {\text{2PO}}_{4}^{3-}\left(aq\right)\\ & {3x}& 2x\end{array}[/latex]
      One unit of [latex]\ce{Mg3(PO4)2}[/latex] provides two units of [latex]{\text{PO}}_{4}^{3-}[/latex] ion and three units of [latex]\ce{Mg^2+}[/latex] ion.
    5. [latex]\begin{array}{cccc}{\text{Ca}}_{5}{\left({\text{PO}}_{4}\right)}_{3}\text{OH}\left(s\right)\rightleftharpoons & {\text{5Ca}}^{\text{2+}}\left(aq\right)+& {\text{3PO}}_{4}^{3-}\left(aq\right)+& {\text{OH}}^{-}\left(aq\right)\\ & {5x}& {3x}& x\end{array}[/latex]
      One unit of [latex]\ce{Ca5(PO4)3OH}[/latex] dissolves into five units of [latex]\ce{Ca^2+}[/latex] ion, three units of [latex]{\text{PO}}_{4}^{3-}[/latex] ion, and one unit of [latex]\ce{OH-}[/latex] ion.
  2. There is no change. A solid has an activity of 1 whether there is a little or a lot.
  3. In each of the following, allow x to be the molar concentration of the ion occurring only once in the formula.
    1. Ksp = [Ag+][I–] = 1.5 – 10–16 = [x2], [x] = 1.2 – 10–8M, [Ag+] = [I–] = 1.2 × 10–8M
    2. Ksp = [latex]{{\text{[Ag}}^{\text{+}}]}^{2}\left[{\text{SO}}_{4}^{2-}\right][/latex] = 1.18 × 10–5 = [2x]2[x], 4x3 = 1.18 × 10–5, x = 1.43 × 10–2M
      As there are 2 Ag+ ions for each [latex]{\text{SO}}_{4}^{2-}[/latex] ion, [Ag+] = 2.86 × 10–2M, [latex]{\text{[SO}}_{4}^{2-}][/latex] = 1.43 × 10–2M; (c) Ksp = [Mn2+]2[OH–]2 = 4.5 × 10–14 = [x][2x]2, 4x3 = 4.5 × 10–14, x = 2.24 × 10–5M.
    3. Since there are two OH– ions for each Mn2+ ion, multiplication of x by 2 gives 4.48 × 10–5M. If the value of x is rounded to the correct number of significant figures, [Mn2+] = 2.2 × 10–5M. [OH–] = 4.5 × 10–5M. If the value of x is rounded before determining the value of [OH–], the resulting value of [OH–] is 4.4 × 10–5M. We normally maintain one additional figure in the calculator throughout all calculations before rounding.
    4. Ksp = [Sr2+][OH–]2 = 3.2 × 10–4 = [x][2x]2, 4x3 = 3.2 × 10–4, x = 4.3 × 10–2M.
      Substitution gives [Sr2+] = 4.3 × 10–2 M, [OH–] = 8.6 × 10–2M
    5. Ksp = [Mg2+]2[OH–]2 = 1.5 × 10–11 = [x][2x]2, 4x3 = 1.5 × 10–11, x = 1.55 × 10–4M, 2x = 3.1 × 10–4.
      Substitution and taking the correct number of significant figures gives [Mg2+] = 1.6 × 10–4M, [OH–] = 3.1 × 10–4M. If the number is rounded first, the first value is still [Mg2+] = 1.6 × 10–4M, but the second is [OH–] = 3.2 × 10–4M.

Glossary

common ion effect: effect on equilibrium when a substance with an ion in common with the dissolved species is added to the solution; causes a decrease in the solubility of an ionic species, or a decrease in the ionization of a weak acid or base

molar solubility: solubility of a compound expressed in units of moles per liter (mol/L)

selective precipitation: process in which ions are separated using differences in their solubility with a given precipitating reagent

solubility product (Ksp): equilibrium constant for the dissolution of a slightly soluble electrolyte

Licenses and Attributions (Click to expand)

CC licensed content, Shared previously

  • Chemistry 2e. Provided by: OpenStax. Located at: https://openstax.org/. License: CC BY: Attribution. License Terms: Access for free at
    https://openstax.org/books/chemistry-2e/pages/1-introduction

All rights reserved content

  • Solubility Product Constant (Ksp). Authored by: Professor Dave Explains. Located at: https://youtu.be/WjiXbemBXkE. License: Other. License Terms: Standard YouTube License
  • Predicting Precipitation With Ksp Values. Authored by: Professor Dave Explains. Located at: https://youtu.be/TBtaeyKkykU. License: Other. License Terms: Standard YouTube License
  • The Common Ion Effect. Authored by: Professor Dave Explains. Located at: https://youtu.be/qawipem0LwA. License: Other. License Terms: Standard YouTube License
definition

License

Icon for the Creative Commons Attribution-NonCommercial-ShareAlike 4.0 International License

Chemistry Fundamentals Copyright © by Dr. Julie Donnelly, Dr. Nicole Lapeyrouse, and Dr. Matthew Rex is licensed under a Creative Commons Attribution-NonCommercial-ShareAlike 4.0 International License, except where otherwise noted.

Share This Book