Chapter 4: Periodic Properties of the Elements

4.2 Electron shielding and effective nuclear charge

https://chem.libretexts.org/Bookshelves/Physical_and_Theoretical_Chemistry_Textbook_Maps/Supplemental_Modules_(Physical_and_Theoretical_Chemistry)/Quantum_Mechanics/10%3A_Multi-electron_Atoms/Multi-Electron_Atoms/Penetration_and_Shielding

https://chem.libretexts.org/Bookshelves/General_Chemistry/Map%3A_A_Molecular_Approach_(Tro)/08%3A_Periodic_Properties_of_the_Elements/8.06%3A_Periodic_Trends_in_the_Size_of_Atoms_and_Effective_Nuclear_Charge

Learning Objectives

  • To understand the basics of electron shielding and penetration

Penetration and shielding are two underlying principles in determining the physical and chemical properties of elements. We can predict basic properties of elements by using shielding and penetration characteristics to assess basic trends.

Introduction

Electrons are negatively charged and are pulled pretty close to each other by their attraction to the positive charge of a nucleus. The electrons are attracted to the nucleus at the same time as electrons repel each other. The balance between attractive and repulsive forces results in shielding. The orbital (n) and subshell (ml) define how close an electron can approach the nucleus. The ability of an electron to get close to the nucleus is penetration.

Coulomb’s Law can be used to describe the attraction and repulsion between atomic particles. The force that an electron feels is dependent on the distance from the nearest charge (i.e., an electron, usually with bigger atoms and on the outer shells) and the amount of charge. More distance between the charges will result in less force, and more charge will have more force of attraction or repulsion. In the simplest case, every electron in an atom would feel the same amount of “pull” from the nucleus. For example, in [latex]\ce{Li}[/latex], all three electrons might “feel” the +3 charge from the nucleus. However, this is not the case when observing atomic behavior. When considering the core electrons (or the electrons closest to the nucleus), the nuclear charge “felt” by the electrons (Effective Nuclear Charge (Zeff)) is close to the actual nuclear charge. As you proceed from the core electrons to the outer valence electrons, Zeff falls significantly. This is because of shielding, or simply the electrons closest to the nucleus decrease the amount of nuclear charge affecting the outer electrons. Shielding is caused by the combination of partial neutralization of nuclear charge by core electrons, and by electron-electron repulsion.

The amount of charge felt by an electron depends on its distance from the nucleus. The closer an electron comes to the nucleus, or the more it penetrates, the stronger its attraction to the nucleus. Core electrons penetrate more and feel more of the nucleus than the other electrons.

$$E=1/(4πϵ_o )⋅(q_1 q_2)/r^2$$

with

  • E is the potential energy
  • q refers to the charged particles
  • r is the separation distance of the particle
  • [latex]\epsilon[/latex]o is a constant and is equal to 8.95 × 10-12 C2/Jm

Shielding

An atom (assuming its atomic number is greater than 2) has core electrons that are extremely attracted to the nucleus in the middle of the atom. However the number of protons in the nucleus are never equal to the number of core electrons (relatively) adjacent to the nucleus. The number of protons increase by one across the periodic table, but the number of core electrons change by periods. The first period has no core electrons, the second has 2, the third has 10, and etc. This number is not equal to the number of protons. So that means that the core electrons feel a stronger pull towards the nucleus than any other electron within the system. The valence electrons are farther out from the nucleus, so they experience a smaller force of attraction.

Shielding refers to the core electrons repelling the outer rings and thus lowering the 1:1 ratio. Hence, the nucleus has “less grip” on the outer electrons and are shielded from them. Electrons that have greater penetration can get closer to the nucleus and effectively block out the charge from electrons that have less proximity. For example, Zeff is calculated by subtracting the magnitude of shielding from the total nuclear charge. The value of Zeff will provide information on how much of a charge an electron actually experiences.

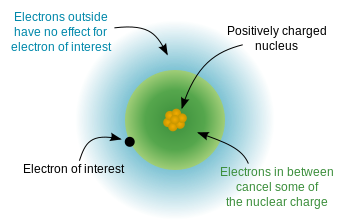
Figure 4.2.1: This image shows how inner electrons can shield outer electrons from the nuclear charge. (CC BY-SA 3.0; from Wikipedia).

Because the order of electron penetration from greatest to least is s, p, d, f; the order of the amount of shielding done is also in the order s, p, d, f.

Since the 2s electron has more density near the nucleus of an atom than a 2p electron, it is said to shield the 2p electron from the full effective charge of the nucleus. Therefore the 2p electron feels a lesser effect of the positively charged nucleus of the atom due to the shielding ability of the electrons closer to the nucleus than itself, (i.e. 2s electron).

These electrons that are shielded from the full charge of the nucleus are said to experience an effective nuclear charge (Zeff)of the nucleus, which is some degree less than the full nuclear charge an electron would feel in a hydrogen atom or hydrogenlike ions. The effective nuclear charge of an atom is given by the equation:

Zeff = Z [latex]-[/latex] S

where

  • Z is the atomic number (number of protons in nucleus) and
  • S is the shielding constant

We can see from this equation that the effective nuclear charge of an atom increases as the number of protons in an atom increases. Therefore as we go from left to right on the periodic table the effective nuclear charge of an atom increases in strength and holds the outer electrons closer and tighter to the nucleus. As we will discuss later on in the chapter, this phenomenon can explain the decrease in atomic radii we see as we go across the periodic table as electrons are held closer to the nucleus due to increase in number of protons and increase in effective nuclear charge.

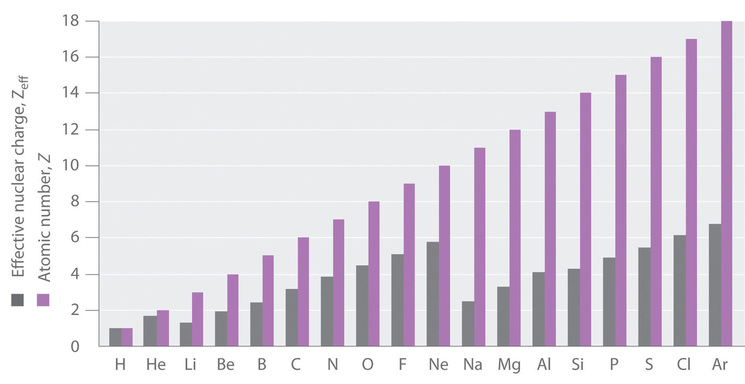
Figure 4.2.2: Relationship between the Effective Nuclear Charge Zeff and the Atomic Number Z for the Outer Electrons of the Elements of the First Three Rows of the Periodic Table. Except for hydrogen, (Zeff is always less than Z, and (Zeff increases from left to right as you go across a row.

Electron Penetration

The approximation in Equation 1 is a good first order description of electron shielding, but the actual Zeff experienced by an electron in a given orbital depends not only on the spatial distribution of the electron in that orbital but also on the distribution of all the other electrons present. This leads to large differences in Zeff for different elements, as shown in Figure 4.2.2 for the elements of the first three rows of the periodic table.

Penetration describes the proximity to which an electron can approach to the nucleus. In a multi-electron system, electron penetration is defined by an electron’s relative electron density (probability density) near the nucleus of an atom (Figure 4.2.3). Electrons in different orbitals have different electron densities around the nucleus. In other words, penetration depends on the shell (n) and subshell (l). Electrons that have greater penetration can get closer to the nucleus and effectively block out the charge from electrons that have less proximity.

For example, a 1s electron (Figure 4.2.3; purple curve) has greater electron density near the nucleus than a 2p electron (Figure 4.2.3; red curve) and has a greater penetration. This related to the shielding constants since the 1s electrons are closer to the nucleus than a 2p electron, hence the 1s screens a 2p electron almost perfectly (S = 1. However, the 2s electron has a lower shielding constant (S < 1 because it can penetrate close to the nucleus in the small area of electron density within the first spherical node (Figure 4.2.3; green curve). In this way the 2s electron can “avoid” some of the shielding effect of the inner 1s electron.

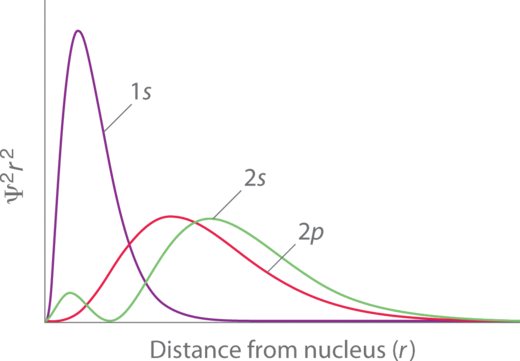
Figure 4.2.3: Orbital Penetration. A comparison of the radial probability distribution of the 2s and 2p orbitals for various states of the hydrogen atom shows that the 2s orbital penetrates inside the 1s orbital more than the 2p orbital does. Consequently, when an electron is in the small inner lobe of the 2s orbital, it experiences a relatively large value of Zeff, which causes the energy of the 2s orbital to be lower than the energy of the 2p orbital.

For the same shell value (n) the penetrating power of an electron follows this trend in subshells (Figure 4.2.3):

s > p > d  [latex]\approx[/latex] f.

for different values of shell (n) and subshell (l), penetrating power of an electron follows this trend:

1s > 2s > 2p > 3s > 3p > 4s > 3d > 4p > 5s > 4d > 5p > 6s > 4f . . .

Table 4.2.1: Effective Nuclear Charges for Selected Atoms
Atom Sublevel Z Zeff
[latex]\ce{H}[/latex] 1s 1 1
[latex]\ce{He}[/latex] 1s 2 1.69
[latex]\ce{Li}[/latex] 1s, 2s 3 2.69, 1.28
[latex]\ce{Be}[/latex] 1s, 2s 4 3.68, 1.91
[latex]\ce{B}[/latex] 1s, 2s, 2p 5 4.68, 2.58, 2.42
[latex]\ce{F}[/latex] 1s, 2s, 2p 9 8.65, 5.13, 5.10
[latex]\ce{Na}[/latex] 1s, 2s, 2p, 3s 11 10.63, 6.57, 6.80, 2.51

Data from E. Clementi and D. L. Raimondi; The Journal of Chemical Physics 38, 2686 (1963).

Because of the effects of shielding and the different radial distributions of orbitals with the same value of n but different values of l, the different subshells are not degenerate in a multielectron atom. For a given value of n, the ns orbital is always lower in energy than the np orbitals, which are lower in energy than the nd orbitals, and so forth. As a result, some subshells with higher principal quantum numbers are actually lower in energy than subshells with a lower value of n; for example, the 4s orbital is lower in energy than the 3d orbitals for most atoms.

Key Concepts and Summary

The calculation of orbital energies in atoms or ions with more than one electron (multielectron atoms or ions) is complicated by repulsive interactions between the electrons. The concept of electron shielding, in which intervening electrons act to reduce the positive nuclear charge experienced by an electron, allows the use of hydrogen-like orbitals and an effective nuclear charge (Zeff) to describe electron distributions in more complex atoms or ions. The degree to which orbitals with different values of l and the same value of n overlap or penetrate filled inner shells results in slightly different energies for different subshells in the same principal shell in most atoms.

Try It

  1. Which orbital is more effective in shielding? 1s or 2p ?
  2. True/False: The greater the penetration of an orbital, the greater the shielding capability of that orbital.
  3. Which of these have the smallest electron affinity? [latex]\ce{B}[/latex], [latex]\ce{C}[/latex], [latex]\ce{N}[/latex], [latex]\ce{O}[/latex], or [latex]\ce{F}[/latex].
  4. Which atom has a stronger effective nuclear charge and why? (assuming [latex]\ce{S}[/latex] is the same in both cases) [latex]\ce{Li}[/latex], or [latex]\ce{N}[/latex]
  5. Why does the Hydrogen electron experiences the full charge of the nucleus without any shielding?
  6. Which atom has a smaller radii? [latex]\ce{Be}[/latex] or [latex]\ce{F}[/latex]?
  7. Which electron has higher energy level? 2s or 2p ? and why?
  8. Why do the orbitals of a hydrogen atom increase energy as follows: 1s < 2s = 2p < 3s = 3p = 3d < 4s = 4p = 4d < . . . .
  9. Which electrons shields better in an atom? 2s or 2p ? 3p or 3d?
  10. Why can we relate classical physics to quantum mechanics when it comes to subatomic activity?
  11. What is penetration?
Show Selected Solutions
  1. 1s
  2. T
  3. nitrogen atom has a stronger effective nuclear charge than lithium due to its greater number of protons in the nucleus holding the electrons tighter.
  4. Hydrogen atom has only one electron total, therefore there are no other, lower energy (more penetrating), electrons available to help shield this electron from the nucleus.
  5. Fluorine has a smaller radii than Beryllium due to its greater number of protons providing a greater effective nuclear charge on the outer electrons and therefore pulling them in tighter and providing a smaller atomic radii.
  6. 2p  has higher energy level because the negatively charged electron experiences less of an effective nuclear charge than the 2s electron.
  7. because a Hydrogen atom has only one electron, that experiences no shielding from other electrons and therefore its energy level only depends on its distance away from the nucleus, which is dependent on it value of (n).
  8. 2s shields the atom better than 2p because the s orbitals is much closer and surrounds the nucleus more than the p orbitals, which extend farther out. 3p shields better than 3d because p orbitals are closer to the nucleus than the 3d orbitals.
  9. Classical physics and quantum mechanics both can deal with subatomic activity such as electron interactions, orbital location, size, and shape, and distances to find forces of attractions.
  10. Penetration is how well the outer electrons are shielded from the nucleus by the core electrons. The outer electrons therefore experience less of an attraction to the nucleus.

Glossary

  • Atomic Radius: The atomic radius decreases from left to right, and increases from top to bottom.
  • Effective Nuclear Charge (Zeff): The effective nuclear charge increases from left to right and increases from top to bottom on the periodic table.
  • Electron penetration: The ability of an electron to get close to the nucleus, which is defined by the orbital (n) and subshell (ml) on how close an electron can approach the nucleus

Contributors and Attributions: The LibreTexts libraries are Powered by MindTouch®and are supported by the Department of Education Open Textbook Pilot Project, the UC Davis Office of the Provost, the UC Davis Library, the California State University Affordable Learning Solutions Program, and Merlot. We also acknowledge previous National Science Foundation support under grant numbers 1246120, 1525057, and 1413739. Unless otherwise noted, LibreTexts content is licensed by CC BY-NC-SA 3.0. Legal. Have questions or comments? For more information contact us at info@libretexts.org or check out our status page at https://status.libretexts.org.

References

  1. Petrucci, Ralph H., William S. Harwood, F. Geoffrey Herring, and Jeffry D. Madura. General Chemistry: Principles and Modern Applications, Ninth Edition. Pearson Education Inc. Upper Saddle River, New Jersey: 2007.
  2. Raymond Chang. Physical Chemistry for Biological Sciences. Sausalito, California: University Science Books, 2005
  3. R. S. Mulliken, Electronic Structures of Molecules and Valence. II General Considerations, Physical Review, vol. 41, pp. 49-71 (1932)
  4. Anastopoulos, Charis (2008). Particle Or Wave: The Evolution of the Concept of Matter in Modern Physics. Princeton University Press. pp. 236–237. ISBN0691135126. http://books.google.com/?id=rDEvQZhpltEC&pg=PA236.

Contributors and Attributions

  • Sidra Ayub (UCD), Alan Chu (UCD)
Licenses and Attributions (Click to expand)

CC licensed content, Shared previously

License

Icon for the Creative Commons Attribution-NonCommercial-ShareAlike 4.0 International License

Chemistry Fundamentals Copyright © by Dr. Julie Donnelly, Dr. Nicole Lapeyrouse, and Dr. Matthew Rex is licensed under a Creative Commons Attribution-NonCommercial-ShareAlike 4.0 International License, except where otherwise noted.

Share This Book