Chapter 15: Acid-Based Equilibria
15.3 Relative Strengths of Acids and Bases
Learning Outcomes
- Assess the relative strengths of acids and bases according to their ionization constants
- Rationalize trends in acid–base strength in relation to molecular structure
- Carry out equilibrium calculations for weak acid–base systems
The relative strength of an acid or base is the extent to which it ionizes when dissolved in water. If the ionization reaction is essentially complete, the acid or base is termed strong; if relatively little ionization occurs, the acid or base is weak. As will be evident throughout the remainder of this chapter, there are many more weak acids and bases than strong ones. The most common strong acids and bases are listed in Table 15.3.1.
The relative strengths of acids may be quantified by measuring their equilibrium constants in aqueous solutions. In solutions of the same concentration, stronger acids ionize to a greater extent, and so yield higher concentrations of hydronium ions than do weaker acids. The equilibrium constant for an acid is called the acid-ionization constant, Ka. For the reaction of an acid HA:
[latex]\text{HA}\left(aq\right)+{\text{H}}_{2}\text{O}\left(l\right)\rightleftharpoons {\text{H}}_{3}{\text{O}}^{+}\left(aq\right)+{\text{A}}^{-}\left(aq\right)[/latex]
the acid ionization constant is written
[latex]{K}_{\text{a}}=\dfrac{\left[{\text{H}}_{3}{\text{O}}^{+}\right]\left[{\text{A}}^{-}\right]}{\text{[HA]}}[/latex]
where the concentrations are those at equilibrium. Although water is a reactant in the reaction, it is the solvent as well, so we do not include [H2O] in the equation. The larger the Ka of an acid, the larger the concentration of [latex]{\text{H}}_{3}{\text{O}}^{+}[/latex]and A− relative to the concentration of the nonionized acid, HA, in an equilibrium mixture, and the stronger the acid. An acid is classified as “strong” when it undergoes complete ionization, in which case the concentration of HA is zero and the acid ionization constant is immeasurably large (Ka ≈ ∞). Acids that are partially ionized are called “weak,” and their acid ionization constants may be experimentally measured. A table of ionization constants for weak acids is provided in Ionization Constants of Weak Acids.
To illustrate this idea, three acid ionization equations and Ka values are shown below. The ionization constants increase from first to last of the listed equations, indicating the relative acid strength increases in the order [latex]\text{CH}_{3}\text{CO}_{2}\text{H}[/latex] < [latex]\text{HNO}_{2}[/latex] < [latex]{\text{HSO}}_{4}^{-}:[/latex]
[latex]{\text{CH}}_{3}{\text{CO}}_{2}\text{H}\left(aq\right)+\text{H}_{2}\text{O}\left(l\right)\rightleftharpoons {\text{H}}_{3}{\text{O}}^{+}\left(aq\right)+{\text{CH}}_{3}{\text{CO}}_{2}^{-}\left(aq\right)\qquad{K}_{\text{a}}=1.8\times {10}^{-5}[/latex]
[latex]{\text{HNO}}_{2}\left(aq\right)+{\text{H}}_{2}\text{O}\left(l\right)\rightleftharpoons {\text{H}}_{3}{\text{O}}^{+}\left(aq\right)+{\text{NO}}_{2}^{-}\left(aq\right)\qquad{K}_{\text{a}}=4.6\times {10}^{-4}[/latex]
[latex]{\text{HSO}}_{4}^{-}\left(aq\right)+{\text{H}}_{2}\text{O}\left(aq\right)\rightleftharpoons {\text{H}}_{3}{\text{O}}^{+}\left(aq\right)+{\text{SO}}_{4}^{2-}\left(aq\right)\qquad{K}_{\text{a}}=1.2\times {10}^{-2}[/latex]
Another measure of the strength of an acid is its percent ionization. The percent ionization of a weak acid is defined in terms of the compostion of an equilibrium mixture:
[latex]\text{% ionization}=\dfrac{{\left[{\text{H}}_{3}{\text{O}}^{+}\right]}_{\text{eq}}}{{\left[\text{HA}\right]}_{0}}\times 100[/latex]
where the numerator is equivalent to the concentration of the acid's conjugate base (per stoichiometry, [A−] = [latex]\ce{[H3O+]}[/latex]). Unlike the Ka value, the percent ionization of a weak acid varies with the initial concentration of acid, typically decreasing as concentration increases. Equilibrium calculations of the sort described later in this chapter can be used to confirm this behavior.
Example 15.3.1: Calculation of Percent Ionization from pH
Calculate the percent ionization of a 0.125-M solution of nitrous acid (a weak acid), with a pH of 2.09.
Show Solution
The percent ionization for an acid is:
[latex]\dfrac{{\left[{\text{H}}_{3}{\text{O}}^{+}\right]}_{\text{eq}}}{{\left[{\text{HNO}}_{2}\right]}_{0}}\times 100[/latex]
The chemical equation for the dissociation of the nitrous acid is: [latex]{\text{HNO}}_{2}\left(aq\right)+{\text{H}}_{2}\text{O}\left(l\right)\rightleftharpoons {\text{NO}}_{2}^{-}\left(aq\right)+{\text{H}}_{3}{\text{O}}^{+}\left(aq\right)[/latex]. Since 10−pH = [latex]\left[\text{H}_{3}\text{O}^{+}\right][/latex], we find that 10−2.09 = 8.1 × 10−3M, so that percent ionization is:
[latex]\dfrac{8.1\times {10}^{-3}}{0.125}\times 100=6.5\%[/latex]
Remember, the logarithm 2.09 indicates a hydronium ion concentration with only two significant figures.
Check Your Learning
As we did with acids, we can measure the relative strengths of bases by measuring their base-ionization constant, (Kb) in aqueous solutions. In solutions of the same concentration, stronger bases ionize to a greater extent, and so yield higher hydroxide ion concentrations than do weaker bases. A stronger base has a larger ionization constant than does a weaker base. For the reaction of a base, B:
[latex]\text{B}\left(aq\right)+{\text{H}}_{2}\text{O}\left(l\right)\rightleftharpoons {\text{HB}}^{+}\left(aq\right)+{\text{OH}}^{-}\left(aq\right)[/latex],
we write the equation for the ionization constant as:
[latex]{K}_{\text{b}}=\dfrac{\left[{\text{HB}}^{+}\right]\left[{\text{OH}}^{-}\right]}{\left[\text{B}\right]}[/latex]
where the concentrations are those at equilibrium. Again, we do not include [latex]\ce{[H2O]}[/latex] in the equation because water is the solvent. The chemical reactions and ionization constants of the three bases shown are:
[latex]{\text{NO}}_{2}^{-}\left(aq\right)+{\text{H}}_{2}\text{O}\left(l\right)\rightleftharpoons {\text{HNO}}_{2}\left(aq\right)+{\text{OH}}^{-}\left(aq\right)\qquad{K}_{\text{b}}=2.22\times {10}^{-11}[/latex]
[latex]{\text{CH}}_{3}{\text{CO}}_{2}^{-}\left(aq\right)+{\text{H}}_{2}\text{O}\left(l\right)\rightleftharpoons {\text{CH}}_{3}{\text{CO}}_{2}\text{H}\left(aq\right)+{\text{OH}}^{-}\left(aq\right)\qquad{K}_{\text{b}}=5.6\times {10}^{-10}[/latex]
[latex]{\text{NH}}_{3}\left(aq\right)+{\text{H}}_{2}\text{O}\left(l\right)\rightleftharpoons {\text{NH}}_{4}^{+}\left(aq\right)+{\text{OH}}^{-}\left(aq\right)\qquad{K}_{\text{b}}=1.8\times {10}^{-5}[/latex]
A table of ionization constants of weak bases appears in Ionization Constants of Weak Bases. As for acids, the relative strength of a base is also reflected in its percent ionization, computed as
[latex]\%\text{ ionization}=[\text{OH}^{-}]_{eq}/[\text{B}]_{0}\times{100}\%[/latex]
but will vary depending on the base ionization constant and the initial concentration of the solution.
Relative Strengths of Conjugate Acid-Base Pairs
Brønsted-Lowry acid-base chemistry is the transfer of protons; thus, logic suggests a relation between the relative strengths of conjugate acid-base pairs. The strength of an acid or base is quantified in its ionization constant, Ka or Kb, which represents the extent of the acid or base ionization reaction. For the conjugate acid-base pair HA / A−, ionization equilibrium equations and ionization constant expressions are
[latex]\text{HA}\left(aq\right)+{\text{H}}_{2}\text{O}\left(l\right)\rightleftharpoons {\text{H}}_{3}{\text{O}}^{+}\left(aq\right)+{\text{A}}^{-}\left(aq\right)\qquad{K}_{\text{a}}=\dfrac{\left[{\text{H}}_{3}{\text{O}}^{+}\right]\left[{\text{A}}^{-}\right]}{\left[\text{HA}\right]}[/latex]
[latex]{\text{A}}^{-}\left(aq\right)+{\text{H}}_{2}\text{O}\left(l\right)\rightleftharpoons {\text{OH}}^{-}\left(aq\right)+\text{HA}\left(aq\right)\qquad{K}_{\text{b}}=\dfrac{\left[\text{HA}\right]\left[\text{OH}\right]}{\left[{\text{A}}^{-}\right]}[/latex]
Adding these two chemical equations yields the equation for the autoionization for water:
[latex]\cancel{\text{HA}\left(aq\right)}+\text{H}_{2}\text{O}\left(l\right)+\cancel{\text{A}^{-}\left(aq\right)}+\text{H}_{2}\text{O}\left(l\right)\rightleftharpoons\text{H}_{3}\text{O}^{+}\left(aq\right)+\cancel{\text{A}^{-}\left(aq\right)}+\text{OH}^{-}\left(aq\right)+\cancel{\text{HA}\left(aq\right)}[/latex]
[latex]{\text{2H}}_{2}\text{O}\left(l\right)\rightleftharpoons {\text{H}}_{3}{\text{O}}^{+}\left(aq\right)+{\text{OH}}^{-}\left(aq\right)[/latex]
As discussed in another chapter on equilibrium, the equilibrium constant for a summed reaction is equal to the mathematical product of the equilibrium constants for the added reactions, and so
[latex]{K}_{\text{a}}\times {K}_{\text{b}}=\dfrac{\left[{\text{H}}_{3}{\text{O}}^{+}\right]\left[{\text{A}}^{-}\right]}{\text{[HA]}}\times \dfrac{\text{[HA]}\left[{\text{OH}}^{-}\right]}{\left[{\text{A}}^{-}\right]}=\left[{\text{H}}_{3}{\text{O}}^{+}\right]\left[{\text{OH}}^{-}\right]={K}_{\text{w}}[/latex]
This equation states the relation between ionization constants for any conjugate acid-base pair, namely, their mathematical product is equal to the ion product of water, Kw. By rearranging this equation, a reciprocal relation between the strengths of a conjugate acid-base pair becomes evident:
[latex]K_{\text{a}}=K_{\text{w}}/K_{\text{b}}\qquad\text{ or }\qquad{K}_{\text{b}}=K_{\text{w}}/K_{\text{a}}[/latex]
The inverse proportional relation between Ka and Kb means the stronger the acid or base, the weaker its conjugate partner. Figure 15.3.1 illustrates this relation for several conjugate acid-base pairs.
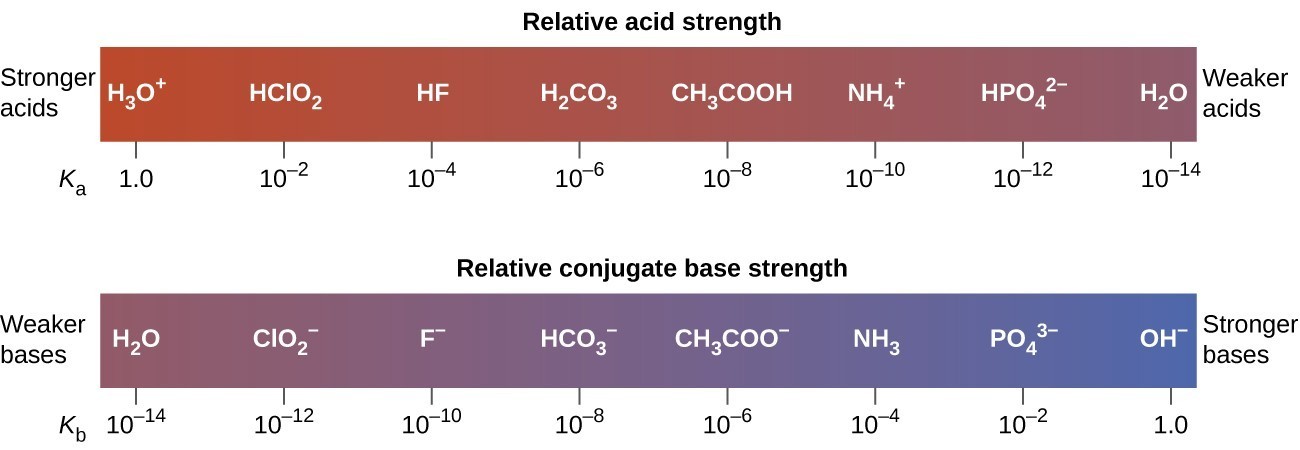
The listing of conjugate acid–base pairs shown in Figure 15.3.2 is arranged to show the relative strength of each species as compared with water, whose entries are highlighted in each of the table’s columns. In the acid column, those species listed below water are weaker acids than water. These species do not undergo acid ionization in water; they are not Bronsted-Lowry acids. All the species listed above water are stronger acids, transferring protons to water to some extent when dissolved in an aqueous solution to generate hydronium ions. Species above water but below hydronium ion are weak acids, undergoing partial acid ionization, wheres those above hydronium ion are strong acids that are completely ionized in aqueous solution.
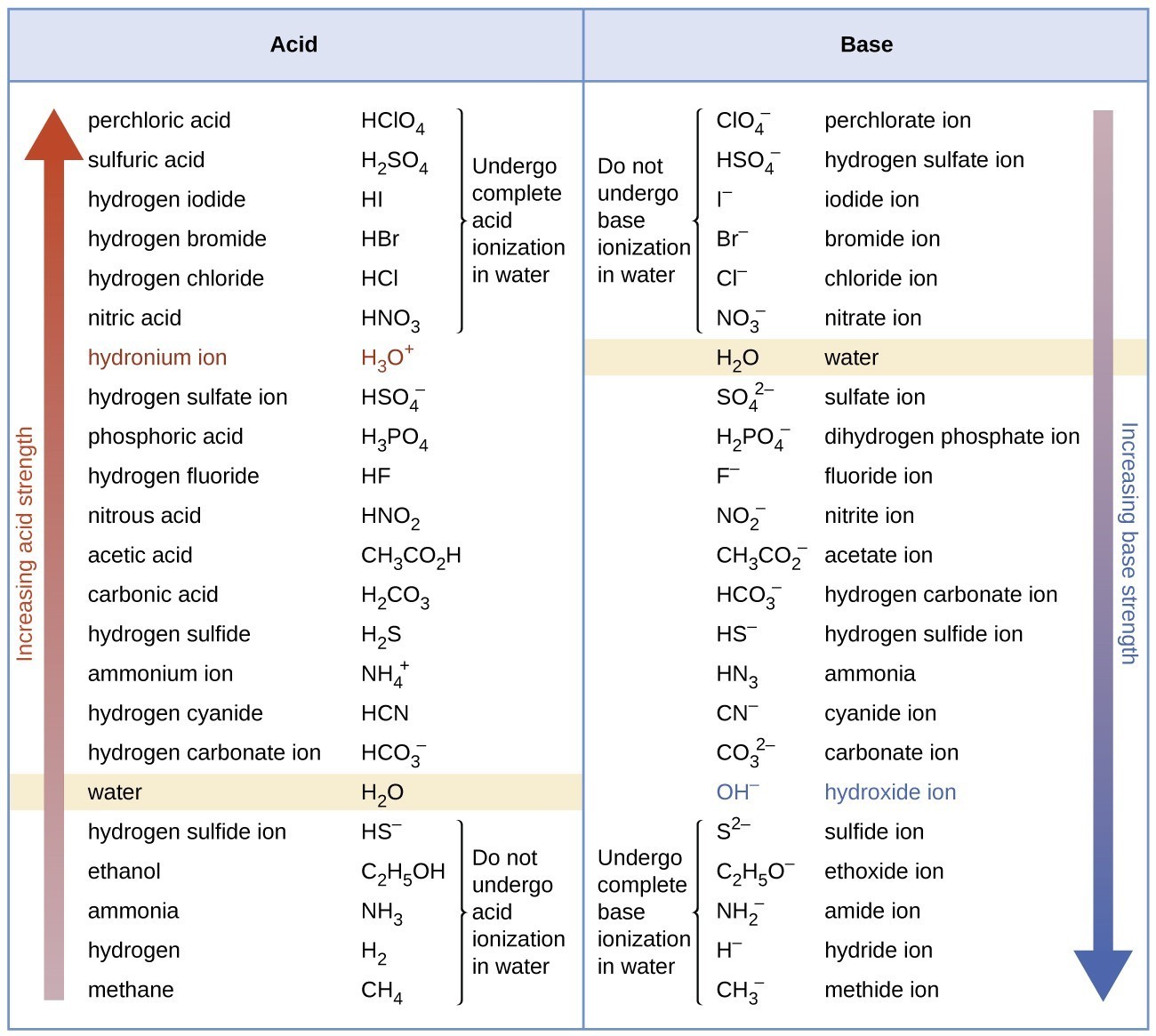
If all these strong acids are completely ionized in water, why does the column indicate they vary in strength, with nitric acid being the weakest and perchloric acid the strongest? Notice that the sole acid species present in an aqueous solution of any strong acid is H3O+(aq), meaning that hydronium ion is the strongest acid that may exist in water; any stronger acid will react completely with water to generate hydronium ions. This limit on the acid strength of solutes in a solution is called a leveling effect. To measure the differences in acid strength for “strong” acids, the acids must be dissolved in a solvent that is less basic than water. In such solvents, the acids will be “weak,” and so any differences in the extent of their ionization can be determined. For example, the binary hydrogen halides HCl, HBr, and HI are strong acids in water but weak acids in ethanol (strength increasing HCl < HBr < HI).
The right column of Figure 15.3.2 lists a number of substances in order of increasing base strength from top to bottom. Following the same logic as for the left column, species listed above water are weaker bases and so they don’t undergo base ionization when dissolved in water. Species listed between water and its conjugate base, hydroxide ion, are weak bases that partially ionize. Species listed below hydroxide ion are strong bases that completely ionize in water to yield hydroxide ions (i.e., they are leveled to hydroxide). A comparison of the acid and base columns in this table supports the reciprocal relation between the strengths of conjugate acid-base pairs. For example, the conjugate bases of the strong acids (top of table) are all of negligible strength. A strong acid exhibits an immeasurably large Ka, and so its conjugate base will exhibit a Kb that is essentially zero:
strong acid: [latex]K_a[/latex] ≈ [latex]\infty[/latex]
conjugate base: [latex]K_b = K_w/K_a = K_w/\infty[/latex] ≈ 0
A similar approach can be used to support the observation that conjugate acids of strong bases (Kb ≈ ∞) are of negligible strength (Ka ≈ 0).
Example 15.3.2: Calculating Ionization Constants for Conjugate Acid-Base Pairs
Use the Kb for the nitrite ion, [latex]{\text{NO}}_{2}^{-}[/latex], to calculate the Ka for its conjugate acid.
Show Solution
Kb for [latex]{\text{NO}}_{2}^{-}[/latex] is given in this section as 2.22 × 10−11. The conjugate acid of [latex]{\text{NO}}_{2}^{-}[/latex] is HNO2; Ka for HNO2 can be calculated using the relationship:
[latex]{K}_{\text{a}}\times {K}_{\text{b}}=1.0\times {10}^{-14}={K}_{\text{w}}[/latex]
Solving for Ka, we get:
[latex]{K}_{\text{a}}=\dfrac{{K}_{\text{w}}}{{K}_{\text{b}}}=\dfrac{1.0\times {10}^{-14}}{2.22\times {10}^{-11}}=4.5\times {10}^{-4}[/latex]
This answer can be verified by finding the Ka for HNO2 in Ionization Constants of Weak Acids.
Check Your Learning
Try It
- Explain why the neutralization reaction of a weak acid and a strong base gives a weakly basic solution.
- Explain why the ionization constant, Ka, for H2SO4 is larger than the ionization constant for H2SO3.
- What is the ionization constant at 25 °C for the weak acid [latex]{\text{CH}}_{3}{\text{NH}}_{3}^{+}[/latex], the conjugate acid of the weak base CH3NH2, Kb = 4.4 × 10−4.
Show Selected Solutions
- The salt ionizes in solution, but the anion slightly reacts with water to form the weak acid. This reaction also forms OH−, which causes the solution to be basic. An example is NaCN. The CN− reacts with water as follows:
- [latex]{\text{CN}}^{-}\left(aq\right)+{\text{H}}_{2}\text{O}\left(l\right)\rightleftharpoons \text{HCN}\left(aq\right)+{\text{OH}}^{-}\left(aq\right)[/latex]
- The oxidation state of the sulfur in H2SO4 is greater than the oxidation state of the sulfur in H2SO3.
- Kw = Ka × Kb; thus,
- [latex]\begin{array}{rcl}{K}_{\text{a}}&=&\frac{{K}_{\text{w}}}{{K}_{\text{b}}}\\{K}_{\text{a}}&=&\frac{1.0\times {10}^{-14}}{4.4\times {10}^{-4}}=2.3\times {10}^{-11}\end{array}[/latex]
Acid- Base Equilibrium Calculations
The chapter on chemical equilibria introduced several types of equilibrium calculations and the various mathematical strategies that are helpful in performing them. These strategies are generally useful for equilibrium systems regardless of chemical reaction class, and so they may be effectively applied to acid-base equilibrium problems. This section presents several example exercises involving equilibrium calculations for acid-base systems.
Table 15.3.2 gives the ionization constants for several weak acids; additional ionization constants can be found in Ionization Constants of Weak Acids.
The ionization constants of several weak bases are given in Table 3 and in Ionization Constants of Weak Bases.
Think about It
Both HF and HCN ionize in water to a limited extent. Which of the conjugate bases, F− or CN−, is the stronger base? See Table 15.3.3.
Try It
- Calculate the equilibrium concentration of the nonionized acids and all ions in a solution that is 0.25 M in HCO2H and 0.10 M in HClO.
- Calculate the equilibrium concentration of the nonionized acids and all ions in a solution that is 0.134 M in HNO2 and 0.120 M in HBrO.
- Calculate the equilibrium concentration of the nonionized bases and all ions in a solution that is 0.25 M in CH3NH2 and 0.10 M in C5H5N (Kb = 1.7 × 10−9).
- Calculate the equilibrium concentration of the nonionized bases and all ions in a solution that is 0.115 M in NH3 and 0.100 M in C6H5NH2.
- Using the Ka values in Ionization Constants of Weak Acids, place [latex]\text{Al}{\left({\text{H}}_{2}\text{O}\right)}_{6}^{3+}[/latex] in the correct location in Figure 15.3.3.
Show Solutions
2. The reactions and equilibrium constants are:
[latex]\begin{array}{l}{\text{HNO}}_{2}\left(aq\right)+{\text{H}}_{2}\text{O}\left(l\right)\rightleftharpoons {\text{H}}_{3}{\text{O}}^{+}\left(aq\right)+{\text{NO}}_{2}^{-}\left(aq\right){K}_{\text{a}}=4.5\times {10}^{-4}\\ \text{HBrO}\left(aq\right)+{\text{H}}_{2}\text{O}\left(l\right)\rightleftharpoons {\text{H}}_{3}{\text{O}}^{+}\left(aq\right)+{\text{BrO}}^{-}\left(aq\right){K}_{\text{a}}=2\times {10}^{-9}\end{array}[/latex]
As Ka is much larger for HNO2 than for HBrO, the first equilibrium will dominate. The equilibrium expression is [latex]{K}_{\text{a}}=\frac{\left[{\text{NO}}_{2}^{-}\right]\left[{\text{H}}_{3}{\text{O}}^{+}\right]}{\left[{\text{HNO}}_{2}\right]}=4.5\times {10}^{-5}[/latex]
The initial and equilibrium concentrations for this system can be written as follows:
| [HNO2] | [H3O+] | [NO2−] | |
|---|---|---|---|
| Initial concentration (M) | 0.134 | 0 | 0 |
| Change (M) | −x | x | x |
| Equilibrium (M) | 0.134 − x | x | x |
Substituting the equilibrium concentrations into the equilibrium expression and making the assumption that (0.134 − x) ≈ 0.134 gives:
[latex]\frac{\left[{\text{NO}}_{2}^{-}\right]\left[{\text{H}}_{3}{\text{O}}^{+}\right]}{\left[{\text{HNO}}_{2}\right]}=\frac{\left(x\right)\left(x\right)}{\left(0.134-x\right)}\approx \frac{\left(x\right)\left(x\right)}{0.134}=4.5\times {10}^{-4}[/latex]
Solving for x gives 7.77 × 10−3M. Because this value is 5.8% of 0.134, our assumption is incorrect. Therefore, we must use the quadratic formula. Using the data gives the following equation: x2 + 4.5 × 10−7x − 6.03 × 10−5 = 0
Using the quadratic formula gives (a = 1, b = 4.5 × 10−4, and c = −6.03 × 10−5)
[latex]\begin{array}{rcl}{ }x&=&\frac{-b\pm \sqrt{{b}^{\text{2+}}-4ac}}{2a}=\frac{-\left(4.5\times {10}^{-4}\right)\pm \sqrt{{\left(4.5\times {10}^{-4}\right)}^{\text{2+}}-4\left(1\right)\left(-6.03\times {10}^{-5}\right)}}{2\left(1\right)}\\{}&=&\frac{-\left(4.5\times {10}^{-4}\right)\pm \left(1.55\times {10}^{-2}\right)}{2}=7.54\times {10}^{-3}M\left(\text{positive root}\right)\end{array}[/latex]
The equilibrium concentrations are therefore:
- [latex]\left[{\text{H}}_{3}{\text{O}}^{+}\right]=\left[{\text{NO}}_{2}^{-}\right]=7.54\times {10}^{-3}=7.5\times {10}^{-3}M[/latex]
- [HNO2] = 0.134 − 7.54 × 10−3 = 0.1264 = 0.126
[OH−] can be calculated using Kw:
[latex]\left[{\text{OH}}^{-}\right]=\frac{{K}_{\text{w}}}{\left[{\text{H}}_{3}{\text{O}}^{+}\right]}=\frac{1.0\times {10}^{-14}}{7.54\times {10}^{-3}}=1.33\times {10}^{-12}=1.3\times {10}^{-12}M[/latex]
Finally, use the other equilibrium to find the other concentrations. Assume for [HBrO] that (0.120 − x) ≈ 0.124 M.
[latex]{K}_{\text{a}}=\frac{\left[{\text{BrO}}^{-}\right]\left[{\text{H}}_{3}{\text{O}}^{+}\right]}{\left[\text{HBrO}\right]}=2\times {10}^{-9}\approx \frac{\left[{\text{BrO}}^{-}\right]\left(7.54\times {10}^{-3}\right)}{0.120}[/latex]
Solving for [BrO−] gives:
- [BrO−] = 3.2 × 10−8 = 3.2 × 10−8M
- [HBrO] = 0.120 − 3.2 × 10−8 = 0.120 M
4. The reactions and equilibrium constants are:
[latex]\begin{array}{l}{}{\text{NH}}_{3}\left(aq\right)+{\text{H}}_{2}\text{O}\left(l\right)\rightleftharpoons {\text{OH}}^{-}\left(aq\right)+{\text{NH}}_{4}^{+}\left(aq\right){K}_{\text{b}}=1.8\times {10}^{-5}\\ {\text{C}}_{6}{\text{H}}_{5}{\text{NH}}_{2}\left(aq\right)+{\text{H}}_{2}\text{O}\left(l\right)\rightleftharpoons {\text{OH}}^{-}\left(aq\right)+{\text{C}}_{6}{\text{H}}_{5}{\text{NH}}_{3}^{+}\left(aq\right){K}_{\text{b}}=4.6\times {10}^{-10}\end{array}[/latex]
As Kb is much larger for NH3 than for C6H5NH2, the first equilibrium will dominate. The equilibrium expression is [latex]{K}_{\text{b}}=\frac{\left[{\text{NH}}_{4}^{+}\right]\left[{\text{OH}}^{-}\right]}{\left[{\text{NH}}_{3}\right]}=1.8\times {10}^{-5}[/latex]
The initial and equilibrium concentrations for this system can be written as follows:
| [NH3] | [OH−] | [NH4+] | |
|---|---|---|---|
| Initial concentration (M) | 0.115 | 0 | 0 |
| Change (M) | −x | x | x |
| Equilibrium (M) | 0.115 − x | x | x |
Substituting the equilibrium concentrations into the equilibrium expression and making the assumption that (0.115 − x) ≈ 0.115 gives:
[latex]\frac{\left[{\text{NH}}_{4}^{+}\right]\left[{\text{OH}}^{-}\right]}{\left[{\text{NH}}_{3}\right]}=\frac{\left(x\right)\left(x\right)}{\left(0.115-x\right)}\approx \frac{\left(x\right)\left(x\right)}{0.115}=1.8\times {10}^{-5}[/latex]
Solving for x gives 1.44 × 10−3M. Because this value is less than 5% of 0.115 M, our assumption is correct. The equilibrium concentrations are therefore:
- [OH−] = [latex]\left[{\text{NO}}_{4}^{+}\right][/latex] = 1.44 × 10−3 = 0.0014 M
- [NH3] = 0.115 − 0.00144 = 0.1136 = 0.144 M
[latex]\left[{\text{H}}_{3}{\text{O}}^{+}\right][/latex] can be calculated using Kw:
[latex]\left[{\text{H}}_{3}{\text{O}}^{+}\right]=\frac{{K}_{\text{w}}}{\left[{\text{OH}}^{-}\right]}=\frac{1.0\times {10}^{-14}}{0.00144}=6.94\times {10}^{-12}=6.9\times {10}^{-12}M[/latex]
Finally, use the other equilibrium to find the other concentrations. Assume for [C6H5NH2] that (0.100 − x) ≈ 0.100 M:
[latex]\left[{\text{H}}_{3}{\text{O}}^{+}\right]=\frac{{K}_{\text{w}}}{\left[{\text{OH}}^{-}\right]}=\frac{1.0\times {10}^{-14}}{0.00144}=6.94\times {10}^{-12}=6.9\times {10}^{-12}M[/latex]
Solving for [latex]\left[{\text{C}}_{6}{\text{H}}_{5}{\text{NH}}_{3}^{+}\right][/latex] gives:
- [latex]\left[{\text{C}}_{6}{\text{H}}_{5}{\text{NH}}_{3}^{+}\right][/latex] = 3.9 × 10−8M
- [C6H5NH2] = 0.100 − 3.19 × 10−8 = 0.100 M
Example 15.3.3: Determination of Ka from Equilibrium Concentrations
Acetic acid is the principal ingredient in vinegar (Figure 15.3.5); that's why it tastes sour. At equilibrium, a solution contains [CH3CO2H] = 0.0787 M and [latex]\left[{\text{H}}_{3}{\text{O}}^{+}\right]=\left[{\text{CH}}_{3}{\text{CO}}_{2}^{-}\right]=0.00118M[/latex]. What is the value of Ka for acetic acid?

Show Solution
We are asked to calculate an equilibrium constant from equilibrium concentrations. At equilibrium, the value of the equilibrium constant is equal to the reaction quotient for the reaction:
[latex]{\text{CH}}_{3}{\text{CO}}_{2}\text{H}\left(aq\right)+{\text{H}}_{2}\text{O}\left(l\right)\rightleftharpoons {\text{H}}_{3}{\text{O}}^{+}\left(aq\right)+{\text{CH}}_{3}{\text{CO}}_{2}^{-}\left(aq\right)[/latex]
[latex]{K}_{\text{a}}=\dfrac{\left[{\text{H}}_{3}{\text{O}}^{+}\right]\left[{\text{CH}}_{3}{\text{CO}}_{2}^{-}\right]}{\left[{\text{CH}}_{3}{\text{CO}}_{2}\text{H}\right]}=\dfrac{\left(0.00118\right)\left(0.00118\right)}{0.0787}=1.77\times {10}^{-5}[/latex]
Check Your Learning
Example 15.3.4: Determination of Kb from Equilibrium Concentrations
Caffeine, C8H10N4O2 is a weak base. What is the value of Kb for caffeine if a solution at equilibrium has [C8H10N4O2] = 0.050 M, [latex]\left[{\text{C}}_{8}{\text{H}}_{10}{\text{N}}_{4}{\text{O}}_{2}{\text{H}}^{+}\right][/latex] = 5.0 × 10−3M, and [OH−] = 2.5 × 10−3M?
Show Solution
At equilibrium, the value of the equilibrium constant is equal to the reaction quotient for the reaction:
[latex]{\text{C}}_{8}{\text{H}}_{10}{\text{N}}_{4}{\text{O}}_{2}\left(aq\right)+{\text{H}}_{2}\text{O}\left(l\right)\rightleftharpoons {\text{C}}_{8}{\text{H}}_{10}{\text{N}}_{4}{\text{O}}_{2}{\text{H}}^{+}\left(aq\right)+{\text{OH}}^{-}\left(aq\right)[/latex]
[latex]{K}_{\text{b}}=\dfrac{\left[{\text{C}}_{8}{\text{H}}_{10}{\text{N}}_{4}{\text{O}}_{2}{\text{H}}^{+}\right]\left[{\text{OH}}^{-}\right]}{\left[{\text{C}}_{8}{\text{H}}_{10}{\text{N}}_{4}{\text{O}}_{2}\right]}=\dfrac{\left(5.0\times {10}^{-3}\right)\left(2.5\times {10}^{-3}\right)}{0.050}=2.5\times {10}^{-4}[/latex]
Check Your Learning
Example 15.3.5: Determination of Ka or Kb from pH
The pH of a 0.0516-M solution of nitrous acid, HNO2, is 2.34. What is its Ka?
[latex]{\text{HNO}}_{2}\left(aq\right)+{\text{H}}_{2}\text{O}\left(l\right)\rightleftharpoons {\text{H}}_{3}{\text{O}}^{+}\left(aq\right)+{\text{NO}}_{2}^{-}\left(aq\right)[/latex]
Show Solution
The nitrous acid concentration provided is a formal concentration, one that does not account for any chemical equilibria that may be established in solution. Such concentrations are treated as “initial” values for equilibrium calculations using the ICE table approach (see previous chapter on ICE tables). Notice the initial value of hydronium ion is listed as approximately zero because a small concentration of H3O+ is present (1 × 10−7 M) due to the autoprotolysis of water. In many cases, such as all the ones presented in this chapter, this concentration is much less than that generated by ionization of the acid (or base) in question and may be neglected.
The pH provided is a logarithmic measure of the hydronium ion concentration resulting from the acid ionization of the nitrous acid, and so it represents an “equilibrium” value for the ICE table:
[latex]\left[{\text{H}}_{3}{\text{O}}^{+}\right]={10}^{-2.34}=0.0046M[/latex]
The ICE table for this system is then:
Finally, we calculate the value of the equilibrium constant using the data in the table:
[latex]{K}_{\text{a}}=\dfrac{\left[{\text{H}}_{3}{\text{O}}^{+}\right]\left[{\text{NO}}_{2}^{-}\right]}{\left[{\text{HNO}}_{2}\right]}=\dfrac{\left(0.0046\right)\left(0.0046\right)}{\left(0.0470\right)}=4.5\times {10}^{-4}[/latex]
Check Your Learning
Example 15.3.6: Equilibrium Concentrations in a Solution of a Weak Acid
Formic acid, HCO2H, is the irritant that causes the body’s reaction to ant stings (Figure 15.3.6).

What is the concentration of hydronium ion and the pH in a 0.534-M solution of formic acid?
[latex]{\text{HCO}}_{2}\text{H}\left(aq\right)+{\text{H}}_{2}\text{O}\left(l\right)\rightleftharpoons {\text{H}}_{3}{\text{O}}^{+}\left(aq\right)+{\text{HCO}}_{2}^{-}\left(aq\right){K}_{\text{a}}=1.8\times {10}^{-4}[/latex]
Show Solution
Step 1: Determine x and equilibrium concentrations
The ICE table for this system is
Substituting the equilibrium concentration terms into the Ka expression gives
[latex]\begin{array}{rcl}{K}_{\text{a}}&=&1.8\times {10}^{-4}=\dfrac{\left[{\text{H}}_{3}{\text{O}}^{+}\right]\left[{\text{HCO}}_{2}^{-}\right]}{\left[{\text{HCO}}_{2}\text{H}\right]}\\{}&=&\dfrac{\left(x\right)\left(x\right)}{0.534-x}=1.8\times {10}^{-4}\end{array}[/latex]
Because the initial concentration of acid is reasonably large and Ka is very small, we assume that x << 0.534, which permits us to simplify the denominator term as (0.534 − x) = 0.534. This gives:
[latex]{K}_{\text{a}}=1.8\times {10}^{-4}=\dfrac{{x}^{\text{2}}}{0.534}[/latex]
Solve for x as follows:
[latex]\begin{array}{rcl}{x}^{\text{2}}&=&0.534\times \left(1.8\times {10}^{-4}\right)=9.6\times {10}^{-5}\\x&=&\sqrt{9.6\times {10}^{-5}}\\&=&9.8\times {10}^{-3} M\end{array}[/latex]
To check the assumption that x is small compared to 0.534, we calculate:
[latex]\dfrac{x}{0.534}=\dfrac{9.8\times{10}^{-3}}{0.534}=1.8\times{10}^{-2}\left(1.8\%\text{ of 0.534}\right)[/latex]
x is less than 5% of the initial concentration; the assumption is valid.
As defined in the ICE table, x is equal to the equilibrium concentration of hydronium ion:
[latex]x=[\text{H}_{3}\text{O}^{+}]=0.0098 M[/latex]
Finally, the pH is calculated to be
[latex]\text{pH}=\text{log}[\text{H}_{3}\text{O}^{+}]=-\text{log}(0.0098)=2.01[/latex]
Check Your Learning
Example 15.3.7 shows that the concentration of products produced by the ionization of a weak base can be determined by the same series of steps used with a weak acid.
Example 15.3.7: Equilibrium Concentrations in a Solution of a Weak Base
Find the concentration of hydroxide ion in a 0.25-M solution of trimethylamine, a weak base:
[latex]{\left({\text{CH}}_{3}\right)}_{3}\text{N}\left(aq\right)+{\text{H}}_{2}\text{O}\left(l\right)\rightleftharpoons {\left({\text{CH}}_{3}\right)}_{3}{\text{NH}}^{+}\left(aq\right)+{\text{OH}}^{-}\left(aq\right)\qquad{K}_{\text{b}}=6.3\times {10}^{-5}[/latex]
Show Solution
The ICE table for this system is

At equilibrium:
[latex]{K}_{\text{b}}=\dfrac{\left[{\left({\text{CH}}_{3}\right)}_{3}{\text{NH}}^{+}\right]\left[{\text{OH}}^{-}\right]}{\left[{\left({\text{CH}}_{3}\right)}_{3}\text{N}\right]}=\dfrac{\left(x\right)\left(x\right)}{0.25-x}=6.3\times {10}^{-5}[/latex]
If we assume that x is small relative to 0.25, then we can replace (0.25 − x) in the preceding equation with 0.25. Solving the simplified equation gives [latex]x=4.0\times {10}^{-3}[/latex].
This change is less than 5% of the initial concentration (0.25), so the assumption is justified. Recall that, for this computation, x is equal to the equilibrium concentration of hydroxide ion in the solution (see earlier tabulation):
[latex]\left[{\text{OH}}^{-}\right]=\text{~}0+x=x=4.0\times {10}^{-3}M[/latex]
[latex]=4.0\times {10}^{-3}M[/latex]
Then calculate pOH as follows:
[latex]\text{pOH}=-\text{log}\left(4.0\times {10}^{-3}\right)=2.40[/latex]
Using the relation introduced in the previous section of this chapter, we get
[latex]\text{pH}+\text{pOH}=\text{p}{K}_{\text{w}}=14.00[/latex]
which permits the computation of pH:
[latex]\text{pH}=14.00-\text{pOH}=14.00 - 2.40=11.60[/latex]
Step 3: Check the work
A check of our arithmetic shows that Kb = 6.3 × 10−5.
Check Your Learning
In some cases, the strength of the weak acid or base and its formal (initial) concentration result in an appreciable ionization. Though the ICE strategy remains effective for these systems, the algebra is a bit more involved because the simplifying assumption that x is negligible can not be made. Calculations of this sort are demonstrated in Example 15.3.8 below.
Example 15.3.8: Calculating Equilibrium Concentrations without simplifying assumptions
Sodium bisulfate, NaHSO4, is used in some household cleansers because it contains the [latex]{\text{HSO}}_{4}^{-}[/latex] ion, a weak acid. What is the pH of a 0.50-M solution of [latex]{\text{HSO}}_{4}^{-}?[/latex]
[latex]{\text{HSO}}_{4}^{-}\left(aq\right)+{\text{H}}_{2}\text{O}\left(l\right)\rightleftharpoons {\text{H}}_{3}{\text{O}}^{+}\left(aq\right)+{\text{SO}}_{4}^{2-}\left(aq\right)\qquad{K}_{\text{a}}=1.2\times {10}^{-2}[/latex]
Show Solution
The ICE table for this system is:

As we begin solving for x, we will find this is more complicated than in previous examples. As we discuss these complications we should not lose track of the fact that it is still the purpose of this step to determine the value of x. At equilibrium:
[latex]{K}_{\text{a}}=1.2\times {10}^{-2}=\dfrac{\left[{\text{H}}_{3}{\text{O}}^{+}\right]\left[{\text{SO}}_{4}^{2-}\right]}{\left[{\text{HSO}}_{4}^{-}\right]}=\dfrac{\left(x\right)\left(x\right)}{0.50-x}[/latex]
If we assume that x is small and approximate (0.50 − x) as 0.50, we find [latex]x=7.7\times {10}^{-2}M[/latex]. When we check the assumption, we calculate:
[latex]\dfrac{x}{{\left[{\text{HSO}}_{4}^{-}\right]}_{\text{i}}}[/latex]
[latex]\dfrac{x}{0.50}=\dfrac{7.7\times {10}^{-2}}{0.50}=0.15\left(15\%\right)[/latex]
The value of x is not less than 5% of 0.50, so the assumption is not valid. We need the quadratic formula to find x.
[latex]{K}_{\text{a}}=1.2\times {10}^{-2}=\dfrac{\left(x\right)\left(x\right)}{0.50-x}[/latex]
Rearranging this equation yields
[latex]6.0\times {10}^{-3}-1.2\times {10}^{-2}x={x}^{2}[/latex]
Writing the equation in quadratic form gives
[latex]{x}^{2}+1.2\times {10}^{-2}x - 6.0\times {10}^{-3}=0[/latex]
Solving for the two roots of this quadratic equation results in a negative value that may be discarded as physically irrelevant and a positive value equal to x. As defined in the ICE table, x is equal to the hydronium concentration.
[latex]\left[{\text{H}}_{3}{\text{O}}^{+}\right]=~0+x=0+7.2\times {10}^{-2}M=7.2\times {10}^{-2}M[/latex]
[latex]\text{pH}=-\text{log}\left[{\text{H}}_{3}{\text{O}}^{+}\right]=-\text{log}(7.2\times {10}^{-2})=1.14[/latex]
Check Your Learning
Try It
Calculate the concentration of all solute species in each of the following solutions of acids or bases. Assume that the ionization of water can be neglected, and show that the change in the initial concentrations can be neglected. Ionization constants can be found in Ionization Constants of Weak Acids and Ionization Constants of Weak Bases.
Solution 1
0.0092 M HClO, a weak acid
Show Solution
The reaction is: [latex]\text{HClO}\left(aq\right)+{\text{H}}_{2}\text{O}\left(l\right)\rightleftharpoons {\text{H}}_{3}{\text{O}}^{+}\left(aq\right)+{\text{ClO}}^{-}\left(aq\right)[/latex]
The equilibrium expression is [latex]{K}_{\text{a}}=\frac{\left[{\text{H}}_{3}{\text{O}}^{+}\right]\left[{\text{ClO}}^{-}\right]}{\left[\text{HClO}\right]}=3.5\times {10}^{-8}[/latex]
The initial and equilibrium concentrations for this system can be written as follows:
| [HClO] | [H3O+] | [ClO−] | |
|---|---|---|---|
| Initial concentration (M) | 0.0092 | 0 | 0 |
| Change (M) | −x | x | x |
| Equilibrium (M) | 0.0092 − x | x | x |
Substituting the equilibrium concentrations into the equilibrium expression and making the assumption that (0.0092 − x) ≈ 0.0092 gives:
[latex]\frac{\left[{\text{H}}_{3}{\text{O}}^{+}\right]\left[{\text{ClO}}^{-}\right]}{\left[\text{HClO}\right]}=\frac{\left(x\right)\left(x\right)}{\left(0.0092-x\right)}\approx \frac{\left(x\right)\left(x\right)}{0.0092}=3.5\times {10}^{-8}[/latex]
Solving for x gives 1.79 × 10−5M. This value is less than 5% of 0.0092, so the assumption that it can be neglected is valid. Thus, the concentrations of solute species at equilibrium are:
- [latex]\left[{\text{H}}_{3}{\text{O}}^{+}\right][/latex] = [ClO] = 1.8 × 10−5M
- [HClO] = 0.0092 − 1.79 × 10−5 = 0.00918 = 0.00092 M
- [latex]\left[{\text{OH}}^{-}\right]=\frac{{K}_{\text{w}}}{\left[{\text{H}}_{3}{\text{O}}^{+}\right]}=\frac{1.0\times {10}^{-14}}{1.79\times {10}^{-5}}=5.6\times {10}^{-10}M[/latex]
Solution 2
0.0784 M C6H5NH2, a weak base
Show Solution
The reaction is [latex]{\text{C}}_{6}{\text{H}}_{5}{\text{NH}}_{2}\left(aq\right)+{\text{H}}_{2}\text{O}\left(l\right)\rightleftharpoons {\text{C}}_{6}{\text{H}}_{5}{\text{NH}}_{3}^{+}\left(aq\right)+{\text{OH}}^{-}\left(aq\right)[/latex]
The equilibrium expression is [latex]{K}_{\text{a}}=\frac{\left[{\text{C}}_{6}{\text{H}}_{5}{\text{NH}}_{3}^{+}\right]\left[{\text{OH}}^{-}\right]}{\left[{\text{C}}_{6}{\text{H}}_{5}{\text{NH}}_{2}\right]}=4.6\times {10}^{-10}[/latex]
The initial and equilibrium concentrations for this system can be written as follows:
| [C6H5NH2] | [C5H5NH3+] | [OH−] | |
|---|---|---|---|
| Initial concentration (M) | 0.0784 | 0 | 0 |
| Change (M) | −x | x | x |
| Equilibrium (M) | 0.0784 − x | x | x |
Substituting the equilibrium concentrations into the equilibrium expression and making the assumption that (0.0784 − x) ≈ 0.0784 gives:
[latex]\frac{\left[{\text{C}}_{6}{\text{H}}_{5}{\text{NH}}_{3}^{+}\right]\left[{\text{OH}}^{-}\right]}{\left[{\text{C}}_{6}{\text{H}}_{5}{\text{NH}}_{2}\right]}=\frac{\left(x\right)\left(x\right)}{\left(0.0784-x\right)}\approx \frac{\left(x\right)\left(x\right)}{0.0784}=4.6\times {10}^{-10}[/latex]
Solving for x gives 6.01 × 10−6M. This value is less than 5% of 0.0784, so the assumption that it can be neglected is valid. Thus, the concentrations of solute species at equilibrium are:
- [latex]\left[{\text{CH}}_{3}{\text{CO}}_{2}^{-}\right][/latex] = [OH−] = 6.0 × 10−6M
- [C6H5NH2] = 0.0784 − 6.01 × 10−6 = 0.007839 = 0.00784
- [latex]\left[{\text{H}}_{3}{\text{O}}^{+}\right]=\frac{{K}_{\text{w}}}{\left[{\text{OH}}^{-}\right]}=\frac{1.0\times {10}^{-14}}{6.01\times {10}^{-6}}=1.7\times {10}^{-9}M[/latex]
Solution 3
0.0810 M HCN, a weak acid
Show Solution
The reaction is [latex]\text{HCN}\left(aq\right)+{\text{H}}_{2}\text{O}\left(l\right)\rightleftharpoons {\text{H}}_{3}{\text{O}}^{+}\left(aq\right)+{\text{CN}}^{-}\left(aq\right)[/latex].
The equilibrium expression is [latex]{K}_{\text{a}}=\frac{\left[{\text{H}}_{3}{\text{O}}^{+}\right]\left[{\text{CN}}^{-}\right]}{\left[\text{HCN}\right]}=4\times {10}^{-10}[/latex]
The initial and equilibrium concentrations for this system can be written as follows:
| [HClO] | [H3O+] | [CN−] | |
|---|---|---|---|
| Initial concentration (M) | 0.0810 | 0 | 0 |
| Change (M) | −x | x | x |
| Equilibrium (M) | 0.0810 − x | x | x |
Substituting the equilibrium concentrations into the equilibrium expression and making the assumption that (0.0810 − x) ≈ 0.0810 gives:
[latex]\frac{\left[{\text{H}}_{3}{\text{O}}^{+}\right]\left[{\text{CN}}^{-}\right]}{\left[\text{HCN}\right]}=\frac{\left(x\right)\left(x\right)}{\left(0.0810-x\right)}\approx \frac{\left(x\right)\left(x\right)}{0.0810}=4\times {10}^{-10}[/latex]
Solving for x gives 5.69 × 10−6M. This value is less than 5% of 0.0810, so the assumption that it can be neglected is valid. Thus, the concentrations of solute species at equilibrium are:
- [latex]\left[{\text{H}}_{3}{\text{O}}^{+}\right][/latex] = [CN−] = 5.7 × 10−6M
- [HCN] = 0.0810 − 5.69 × 10−6 = 0.08099 = 0.0810 M
- [latex]\left[{\text{OH}}^{-}\right]=\frac{{K}_{\text{w}}}{\left[{\text{H}}_{3}{\text{O}}^{+}\right]}=\frac{1.0\times {10}^{-14}}{5.69\times {10}^{-6}}=1.8\times {10}^{-9}M[/latex]
Solution 4
0.11 M (CH3)3N, a weak base
Show Solution
The reaction is [latex]{\left({\text{CH}}_{3}\right)}_{3}\text{N}\left(aq\right)+{\text{H}}_{2}\text{O}\left(l\right)\rightleftharpoons {\left({\text{CH}}_{3}\right)}_{3}{\text{NH}}^{+}\left(aq\right)+{\text{OH}}^{-}\left(aq\right)[/latex]
The equilibrium expression is [latex]{K}_{\text{b}}=\frac{\left[{\left({\text{CH}}_{3}\right)}_{3}{\text{NH}}^{+}\right]\left[{\text{OH}}^{-}\right]}{\left[{\left({\text{CH}}_{3}\right)}_{3}\text{N}\right]}=7.4\times {10}^{-5}[/latex]
The initial and equilibrium concentrations for this system can be written as follows:
| [(CH3)3N] | [(CH3)3NH+] | [OH−] | |
|---|---|---|---|
| Initial concentration (M) | 0.11 | 0 | 0 |
| Change (M) | −x | x | x |
| Equilibrium (M) | 0.11 − x | x | x |
Substituting the equilibrium concentrations into the equilibrium expression and making the assumption that (0.11 − x) ≈ 0.11 gives:
[latex]\frac{\left[{\left({\text{CH}}_{3}\right)}_{3}{\text{NH}}^{+}\right]\left[{\text{OH}}^{-}\right]}{\left[{\left({\text{CH}}_{3}\right)}_{3}\text{N}\right]}=\frac{\left(x\right)\left(x\right)}{\left(0.11-x\right)}\approx \frac{\left(x\right)\left(x\right)}{0.11}=7.4\times {10}^{-5}[/latex]
Solving for x gives 2.85 × 10−3M. This value is less than 5% of 0.11, so the assumption that it can be neglected is valid. Thus, the concentrations of solute species at equilibrium are:
- [latex]\left[{\left({\text{CH}}_{3}\right)}_{3}{\text{NH}}^{+}\right][/latex] = [OH−] = 2.9 × 10−3M
- [(CH3)3N] = 0.11 − 2.85 × 10−3 = 0.107 = 0.11 M
- [latex]\left[{\text{H}}_{3}{\text{O}}^{+}\right]=\frac{{K}_{\text{w}}}{\left[{\text{OH}}^{-}\right]}=\frac{1.0\times {10}^{-14}}{2.85\times {10}^{-3}}=3.5\times {10}^{-12}M[/latex]
Solution 5
0.120 M [latex]\text{Fe}{\left({\text{H}}_{2}\text{O}\right)}_{6}^{2+}[/latex] a weak acid, Ka = 1.6 × 10−7
Show Solution
The reaction is [latex]\text{Fe}{\left({\text{H}}_{2}\text{O}\right)}_{6}^{2+}\left(aq\right)+{\text{H}}_{2}\text{O}\left(l\right)\rightleftharpoons \text{Fe}{\left({\text{H}}_{2}\text{O}\right)}_{5}{\left(\text{OH}\right)}^{+}\left(aq\right)+{\text{H}}_{3}{\text{O}}^{+}\left(aq\right)[/latex]
The equilibrium expression is [latex]{K}_{\text{a}}=\frac{\left[\text{Fe}{\left({\text{H}}_{2}\text{O}\right)}_{5}{\left(\text{OH}\right)}^{+}\right]\left[{\text{H}}_{3}{\text{O}}^{+}\right]}{\left[\text{Fe}{\left({\text{H}}_{2}\text{O}\right)}_{6}^{2+}\right]}=1.6\times {10}^{-7}[/latex]
The initial and equilibrium concentrations for this system can be written as follows:
| [Fe(H2O)62+] | [H3O+] | [Fe(H2O)5(OH)+] | |
|---|---|---|---|
| Initial concentration (M) | 0.120 | 0 | 0 |
| Change (M) | −x | x | x |
| Equilibrium (M) | 0.120 − x | x | x |
Substituting the equilibrium concentrations into the equilibrium expression and making the assumption that (0.120 − x) ≈ 0.120 gives:
[latex]\frac{\left[\text{Fe}{\left({\text{H}}_{2}\text{O}\right)}_{5}{\left(\text{OH}\right)}^{+}\right]\left[{\text{H}}_{3}{\text{O}}^{+}\right]}{\left[\text{Fe}{\left({\text{H}}_{2}\text{O}\right)}_{6}^{2+}\right]}=\frac{\left(x\right)\left(x\right)}{\left(0.120-x\right)}\approx \frac{\left(x\right)\left(x\right)}{0.120}=1.6\times {10}^{-7}[/latex]
Solving for x gives 1.39 × 10−4M. This value is less than 5% of 0.120, so the assumption that it can be neglected is valid. Thus, the concentrations of solute species at equilibrium are:
- [latex]\left[\text{Fe}{\left({\text{H}}_{2}\text{O}\right)}_{5}{\left(\text{OH}\right)}^{+}\right][/latex] = [latex]\left[{\text{H}}_{3}{\text{O}}^{+}\right][/latex] = 1.4 × 10−4M
- [latex]\left[\text{Fe}{\left({\text{H}}_{2}\text{O}\right)}_{6}^{2+}\right][/latex] = 0.120 − 1.39 × 10−4 = 0.1199 = 0.120 M
- [latex]\left[{\text{OH}}^{-}\right]=\frac{{K}_{\text{w}}}{\left[{\text{H}}_{3}{\text{O}}^{+}\right]}=\frac{1.0\times {10}^{-14}}{1.39\times {10}^{-4}}=7.2\times {10}^{-11}M[/latex]
Effect of Molecular Structure on Acid-Base Strength
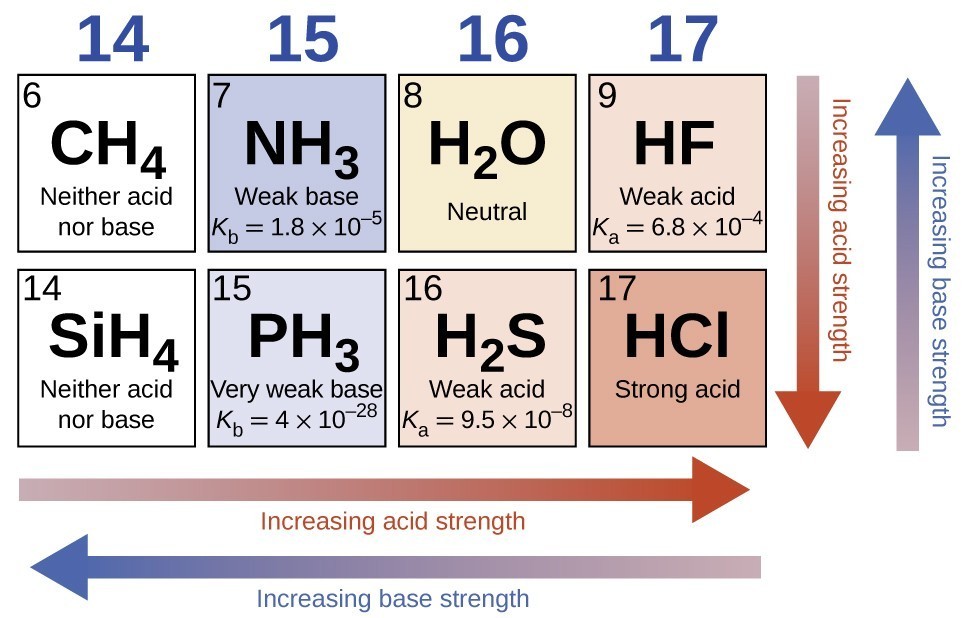
In the absence of any leveling effect, the acid strength of binary compounds of hydrogen with nonmetals (A) increases as the H-A bond strength decreases down a group in the periodic table. For group 7A, the order of increasing acidity is HF < HCl < HBr < HI. Likewise, for group 6A, the order of increasing acid strength is H2O < H2S < H2Se < H2Te.
Across a row in the periodic table, the acid strength of binary hydrogen compounds increases with increasing electronegativity of the nonmetal atom because the polarity of the H-A bond increases. Thus, the order of increasing acidity (for removal of one proton) across the second row is CH4 < NH3 < H2O < HF; across the third row, it is SiH4 < PH3 < H2S < HCl (see Figure 15.3.7).
Ternary Acids and Bases
Compounds containing oxygen and one or more hydroxyl (OH) groups can be acidic, basic, or amphoteric, depending on the position in the periodic table of the central atom E, the atom bonded to the hydroxyl group. Such compounds have the general formula OnE(OH)m, and include sulfuric acid, O2S(OH)2, sulfurous acid, OS(OH)2, nitric acid, O2NOH, perchloric acid, O3ClOH, aluminum hydroxide, Al(OH)3, calcium hydroxide, Ca(OH)2, and potassium hydroxide, KOH:

If the central atom, E, has a low electronegativity, its attraction for electrons is low. Little tendency exists for the central atom to form a strong covalent bond with the oxygen atom, and bond a between the element and oxygen is more readily broken than bond b between oxygen and hydrogen. Hence bond a is ionic, hydroxide ions are released to the solution, and the material behaves as a base—this is the case with Ca(OH)2 and KOH. Lower electronegativity is characteristic of the more metallic elements; hence, the metallic elements form ionic hydroxides that are by definition basic compounds.
If, on the other hand, the atom E has a relatively high electronegativity, it strongly attracts the electrons it shares with the oxygen atom, making bond a relatively strongly covalent. The oxygen-hydrogen bond, bond b, is thereby weakened because electrons are displaced toward E. Bond b is polar and readily releases hydrogen ions to the solution, so the material behaves as an acid. High electronegativities are characteristic of the more nonmetallic elements. Thus, nonmetallic elements form covalent compounds containing acidic −OH groups that are called oxyacid.
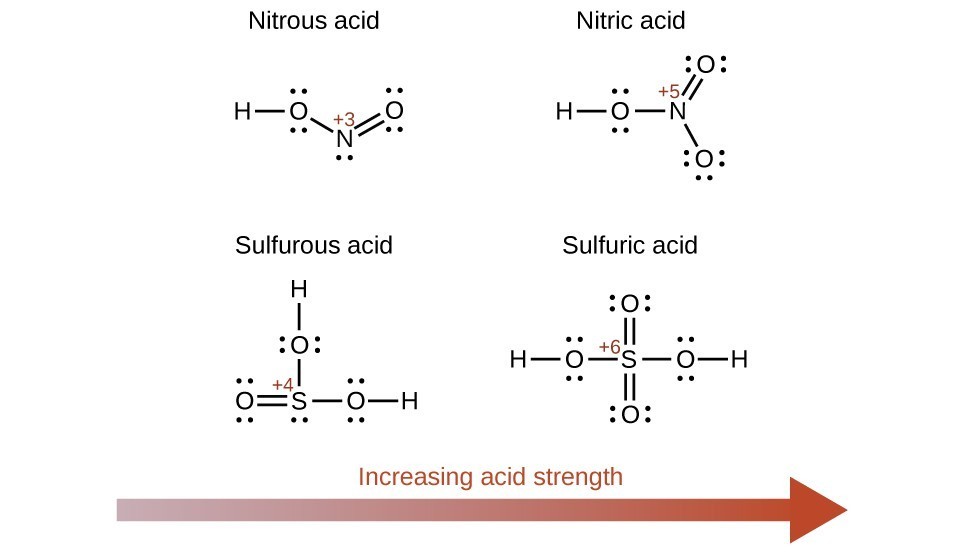
Increasing the oxidation number of the central atom E also increases the acidity of an oxyacid because this increases the attraction of E for the electrons it shares with oxygen and thereby weakens the O-H bond. Sulfuric acid, H2SO4, or O2S(OH)2 (with a sulfur oxidation number of +6), is more acidic than sulfurous acid, H2SO3, or OS(OH)2 (with a sulfur oxidation number of +4). Likewise nitric acid, HNO3, or O2NOH (N oxidation number = +5), is more acidic than nitrous acid, HNO2, or ONOH (N oxidation number = +3). In each of these pairs, the oxidation number of the central atom is larger for the stronger acid (Figure 15.3.8).
Hydroxy compounds of elements with intermediate electronegativities and relatively high oxidation numbers (for example, elements near the diagonal line separating the metals from the nonmetals in the periodic table) are usually amphoteric. This means that the hydroxy compounds act as acids when they react with strong bases and as bases when they react with strong acids. The amphoterism of aluminum hydroxide, which commonly exists as the hydrate Al(H2O)3(OH)3, is reflected in its solubility in both strong acids and strong bases. In strong bases, the relatively insoluble hydrated aluminum hydroxide, Al(H2O)3(OH)3, is converted into the soluble ion, [latex]{\left[\text{Al}{\left({\text{H}}_{2}\text{O}\right)}_{2}{\left(\text{OH}\right)}_{4}\right]}^{-}[/latex], by reaction with hydroxide ion:
[latex]\text{Al}{\left({\text{H}}_{2}\text{O}\right)}_{3}{\left(\text{OH}\right)}_{3}\left(aq\right)+{\text{OH}}^{-}\left(aq\right)\rightleftharpoons {\text{H}}_{2}\text{O}\left(l\right)+{\left[\text{Al}{\left({\text{H}}_{2}\text{O}\right)}_{2}{\left(\text{OH}\right)}_{4}\right]}^{-}\left(aq\right)[/latex]
In this reaction, a proton is transferred from one of the aluminum-bound H2O molecules to a hydroxide ion in solution. The Al(H2O)3(OH)3 compound thus acts as an acid under these conditions. On the other hand, when dissolved in strong acids, it is converted to the soluble ion [latex]{\left[\text{Al}{\left({\text{H}}_{2}\text{O}\right)}_{6}\right]}^{3+}[/latex] by reaction with hydronium ion:
[latex]{\text{3H}}_{3}{\text{O}}^{+}\left(aq\right)+\text{Al}{\left({\text{H}}_{2}\text{O}\right)}_{3}{\left(\text{OH}\right)}_{3}\left(aq\right)\rightleftharpoons \text{Al}{\left({\text{H}}_{2}\text{O}\right)}_{6}^{3+}\left(aq\right)+{\text{3H}}_{2}\text{O}\left(l\right)[/latex]
In this case, protons are transferred from hydronium ions in solution to Al(H2O)3(OH)3, and the compound functions as a base.
Try It
- Propionic acid, C2H5CO2H (Ka = 1.34 × 10−5), is used in the manufacture of calcium propionate, a food preservative. What is the hydronium ion concentration in a 0.698-M solution of C2H5CO2H?
- White vinegar is a 5.0% by mass solution of acetic acid in water. If the density of white vinegar is 1.007 g/cm3, what is the pH?
- The ionization constant of lactic acid, CH3CH(OH)CO2H, an acid found in the blood after strenuous exercise, is 1.36 × 10−4. If 20.0 g of lactic acid is used to make a solution with a volume of 1.00 L, what is the concentration of hydronium ion in the solution?
- Nicotine, C10H14N2, is a base that will accept two protons (K1 = 7 × 10−7, K2 = 1.4 × 10−11). What is the concentration of each species present in a 0.050-M solution of nicotine?
- The pH of a 0.20-M solution of HF is 1.92. Determine Ka for HF from these data.
- The pH of a 0.15-M solution of [latex]{\text{HSO}}_{4}^{-}[/latex] is 1.43. Determine Ka for [latex]{\text{HSO}}_{4}^{-}[/latex] from these data.
- The pH of a 0.10-M solution of caffeine is 11.16. Determine Kb for caffeine from these data:
- The pH of a solution of household ammonia, a 0.950 M solution of NH3, is 11.612. Determine Kb for NH3 from these data.
Show Solutions
2. First, find the mass of acetic acid. d = 1.007 g/cm3. Take 1.0 L of solution to have the quantities on a mole basis. Then, since 1000 cm3 = 1.0 L, 1000 cm3 × 1.007 g/cm3 = 1007 g in 1.0 L. Then, 5.00% of this is the mass of acetic acid:
[latex]\text{Mass (acetic acid)}=\text{1007 g}\times \frac{5.0%}{100%}=\text{50.35 g}[/latex]
Now calculate the number of moles of acetic acid present. The molar mass of acetic acid is 60.053 g/mol:
[latex]\text{mol acetic acid}=\frac{50.35\cancel{\text{g}}}{60.053\cancel{\text{g}}{\text{mol}}^{-1}}=\text{0.838 mol}[/latex]
From the moles of acetic acid and Ka, calculate [latex]\left[{\text{H}}_{3}{\text{O}}^{+}\right]:[/latex]
[latex]{K}_{\text{a}}=1.8\times {10}^{-5}=\frac{\left[{\text{CH}}_{3}{\text{CO}}_{2}^{-}\right]\left[{\text{H}}_{3}{\text{O}}^{+}\right]}{\left[{\text{CH}}_{3}{\text{CO}}_{2}\text{H}\right]}[/latex]
| [CH3CO2H] | [H3O+] | [CH3CO2−] | |
|---|---|---|---|
| Initial concentration (M) | 0.838 | 0 | 0 |
| Change (M) | −x | x | x |
| Equilibrium (M) | 0.838 − x | x | x |
Substitution gives: [latex]{K}_{\text{a}}=1.8\times {10}^{-5}=\frac{{x}^{\text{2}}}{0.838-x}[/latex]
Drop x because it is small in comparison with 0.838 M.
- x2 = 0.838(1.8 × 10−5) = 1.508 × 10−5 = 3.88 × 10−3 = 2.41
- pH = −log(3.88 × 10−3) = 2.41
4.
[latex]\begin{array}{l}{ }{\text{C}}_{10}{\text{H}}_{14}{\text{N}}_{2}\left(aq\right)+{\text{H}}_{2}\text{O}\left(l\right)\rightleftharpoons {\text{C}}_{10}{\text{H}}_{14}{\text{N}}_{2}{\text{H}}^{+}\left(aq\right)+{\text{OH}}^{-}\left(aq\right)\left({K}_{\text{b1}}=7\times {10}^{-7}\right)\\ {\text{C}}_{10}{\text{H}}_{14}{\text{N}}_{2}{\text{H}}^{+}\left(aq\right)+{\text{H}}_{2}\text{O}\left(l\right)\rightleftharpoons {\text{C}}_{10}{\text{H}}_{14}{\text{N}}_{2}{\text{H}}_{2}^{2+}\left(aq\right)+{\text{OH}}^{-}\left(aq\right)\left({K}_{\text{b2}}=1.4\times {10}^{-11}\right)\end{array}[/latex]
First set up a concentration table:
| [C10H14N2] | [C10H14N2H+] | [OH−] | |
|---|---|---|---|
| Initial concentration (M) | 0.050 | 0 | 0 |
| Change (M) | −x | x | x |
| Equilibrium (M) | 0.050 − x | x | x |
Substituting the equilibrium concentrations into the equilibrium equation and making the assumption that (0.050 − x) = 0.050, we get:
[latex]\begin{array}{rcl}{K}_{\text{b1}}&=&\frac{\left[{\text{C}}_{10}{\text{H}}_{14}{\text{N}}_{2}{\text{H}}^{+}\right]\left[{\text{OH}}^{-}\right]}{\left[{\text{C}}_{10}{\text{H}}_{14}{\text{N}}_{2}\right]}=7\times {10}^{-7}\\{}&=&\frac{\left(x\right)\left(x\right)}{\left(0.050-x\right)}=\frac{{x}^{\text{2+}}}{0.050}=7\times {10}^{-7}\end{array}[/latex]
Solving for x gives 1.87 × 10−4 = 2 × 10−4M = [OH−]
Because x is less than 5% of 0.050 and [OH−] is greater than 4.5 × 10−7 M, our customary assumptions are justified. We can calculate
- [C10H14N2] = 0.050 − x = 0.050 − 2 × 10−4 = 0.048 M
- [OH−] = [latex]\left[{\text{C}}_{10}{\text{H}}_{14}{\text{N}}_{2}{\text{H}}^{+}\right][/latex] = x = 2 × 10−4M
Now calculate the concentration of [latex]{\text{C}}_{10}{\text{H}}_{2}{\text{N}}_{2}{\text{H}}_{2}^{2+}[/latex] in a solution with [OH−] and [latex]\left[{\text{C}}_{10}{\text{H}}_{2}{\text{N}}_{2}{\text{H}}_{2}^{2+}\right][/latex] equal to 2 × 10−4M. The equilibrium between these species is
[latex]{\text{C}}_{10}{\text{H}}_{14}{\text{N}}_{2}{\text{H}}^{+}\left(aq\right)+{\text{H}}_{2}\text{O}\left(l\right)\rightleftharpoons {\text{C}}_{10}{\text{H}}_{14}{\text{N}}_{2}{\text{H}}_{2}^{\text{2+}}\left(aq\right)+{\text{OH}}^{-}\left(aq\right)[/latex]
We know [C10H14N2H+] and [OH−], so we can calculate the concentration of [latex]{\text{C}}_{10}{\text{H}}_{2}{\text{N}}_{2}{\text{H}}_{2}^{2+}[/latex] from the equilibrium expression:
[latex]\begin{array}{rcl}{}{K}_{\text{b2}}&=&\frac{\left[{\text{C}}_{10}{\text{H}}_{14}{\text{N}}_{2}{\text{H}}_{2}^{2+}\right]\left[{\text{OH}}^{-}\right]}{\left[{\text{C}}_{10}{\text{H}}_{14}{\text{N}}_{2}{\text{H}}^{+}\right]}=1.4\times {10}^{-11}\\{}&=&\frac{\left[{\text{C}}_{10}{\text{H}}_{14}{\text{N}}_{2}{\text{H}}_{2}^{2+}\right]\left[2\times {10}^{-4}\right]}{\left[2\times {10}^{-4}\right]}\\ \left[{\text{C}}_{10}{\text{H}}_{14}{\text{N}}_{2}{\text{H}}_{2}^{2+}\right]&=&1.4\times {10}^{-11}M\end{array}[/latex]
The concentration of OH− produced in this ionization is equal to the concentration of [latex]{\text{C}}_{10}{\text{H}}_{2}{\text{N}}_{2}{\text{H}}_{2}^{2+}[/latex], 1.4 × 10−11M, which is much smaller than the 2 ×10−4M produced in the first ionization; therefore, we are justified in neglecting the OH− formed from [latex]{\text{C}}_{10}{\text{H}}_{14}{\text{N}}_{2}{\text{H}}^{+}[/latex].
We can now calculate the concentration of H2O+ present from the ionization of water:
Ka = 1 × 10−14 = [latex]\left[{\text{H}}_{3}{\text{O}}^{+}\right][/latex] [OH−]
[latex]\left[{\text{H}}_{3}{\text{O}}^{+}\right]=\frac{1\times {10}^{-14}}{\left[{\text{OH}}^{-}\right]}=\frac{1\times {10}^{-14}}{1.9\times {10}^{-4}}=5.3\times {10}^{-11}M[/latex]
We can now summarize the concentrations of all species in solution as follows:
- [C10H14N2] = 0.049 M
- [latex]\left[{\text{C}}_{10}{\text{H}}_{14}{\text{N}}_{2}{\text{H}}^{+}\right][/latex] = 1.9 × 10−4 M
- [latex]\left[{\text{C}}_{10}{\text{H}}_{14}{\text{N}}_{2}{\text{H}}_{2}^{2+}\right]=1.4\times {10}^{-11}M[/latex]
- [OH−] = 1.9 × 10−4M
- [latex]\left[{\text{H}}_{3}{\text{O}}^{+}\right][/latex] = 5.3 × 10−11M
6. The reaction is [latex]{\text{HSO}}_{4}^{-}\left(aq\right)+{\text{H}}_{2}\text{O}\left(l\right)\rightleftharpoons {\text{H}}_{3}{\text{O}}^{+}\left(aq\right)+{\text{SO}}_{2}^{2-}\left(aq\right)[/latex].
The concentrations at equilibrium are [latex]\left[{\text{SO}}_{4}^{2-}\right][/latex] = [latex]\left[{\text{H}}_{3}{\text{O}}^{+}\right][/latex] = 10−pH = 10−1.43 = 0.0372 M
- [HF] = 0.15 − 0.0372 M = 0.113 M
- [latex]{K}_{\text{a}}=\frac{\left[{\text{SO}}_{4}^{2-}\right]\left[{\text{H}}_{3}{\text{O}}^{+}\right]}{\left[{\text{HSO}}_{4}^{-}\right]}=\frac{\left(0.0372\right)\left(0.0372\right)}{\left(0.113\right)}=1.2\times {10}^{-2}[/latex]
8. The reaction is [latex]{\text{NH}}_{3}\left(aq\right)+{\text{H}}_{2}\text{O}\left(l\right)\rightleftharpoons {\text{NH}}_{4}^{+}\left(aq\right)+{\text{OH}}^{-}\left(aq\right)[/latex].
The pOH can be determined from pOH = 14.000 − pH = 14.000 − 11.612 = 2.388. Therefore, the concentrations at equilibrium are [latex]\left[{\text{NH}}_{4}^{+}\right][/latex] = [OH−] = 10−pOH = 10−2.388 = 0.004093 M
- [NH3] = 0.950 − 0.004093 = 0.9459 M
- [latex]{K}_{\text{b}}=\frac{\left[{\text{NH}}_{4}^{+}\right]\left[{\text{OH}}^{-}\right]}{\left[{\text{NH}}_{3}\right]}=\frac{\left(0.004093\right)\left(0.004093\right)}{\left(0.9459\right)}=1.77\times {10}^{-5}[/latex]
Key Concepts and Summary
The strengths of Brønsted-Lowry acids and bases in aqueous solutions can be determined by their acid or base ionization constants. Stronger acids form weaker conjugate bases, and weaker acids form stronger conjugate bases. Thus strong acids are completely ionized in aqueous solution because their conjugate bases are weaker bases than water. Weak acids are only partially ionized because their conjugate bases are strong enough to compete successfully with water for possession of protons. Strong bases react with water to quantitatively form hydroxide ions. Weak bases give only small amounts of hydroxide ion. The strengths of the binary acids increase from left to right across a period of the periodic table (CH4 < NH3 < H2O < HF), and they increase down a group (HF < HCl < HBr < HI). The strengths of oxyacids that contain the same central element increase as the oxidation number of the element increases (H2SO3 < H2SO4). The strengths of oxyacids also increase as the electronegativity of the central element increases [H2SeO4 < H2SO4].
Key Equations
- [latex]{K}_{\text{a}}=\frac{\left[{\text{H}}_{3}{\text{O}}^{+}\right]\left[{\text{A}}^{-}\right]}{\left[\text{HA}\right]}[/latex]
- [latex]{K}_{\text{b}}=\frac{\left[{\text{HB}}^{+}\right]\left[{\text{OH}}^{-}\right]}{\left[\text{B}\right]}[/latex]
- Ka × Kb = 1.0 × 10−14 = Kw
- [latex]\text{Percent ionization}=\frac{{\left[{\text{H}}_{3}{\text{O}}^{+}\right]}_{\text{eq}}}{{\left[\text{HA}\right]}_{0}}\times 100[/latex]
Try It
- The odor of vinegar is due to the presence of acetic acid, CH3CO2H, a weak acid. List, in order of descending concentration, all of the ionic and molecular species present in a 1-M aqueous solution of this acid.
- Household ammonia is a solution of the weak base NH3 in water. List, in order of descending concentration, all of the ionic and molecular species present in a 1-M aqueous solution of this base.
- Which base, CH3NH2 or (CH3)2NH, is the strongest base? Which conjugate acid, [latex]{\left({\text{CH}}_{3}\right)}_{2}{\text{NH}}_{2}^{+}[/latex] or (CH3)2NH, is the strongest acid?
- Which is the stronger acid, [latex]{\text{NH}}_{4}^{+}[/latex] or HBrO?
- Which is the stronger base, (CH3)3N or [latex]{\text{H}}_{2}{\text{BO}}_{3}^{-}?[/latex]
- Predict which acid in each of the following pairs is the stronger and explain your reasoning for each.
- H2O or HF
- B(OH)3 or Al(OH)3
- [latex]{\text{HSO}}_{3}^{-}[/latex] or [latex]{\text{HSO}}_{4}^{-}[/latex]
- NH3 or H2S
- H2O or H2Te
- Predict which compound in each of the following pairs of compounds is more acidic and explain your reasoning for each.
- [latex]{\text{HSO}}_{4}^{-}[/latex] or [latex]{\text{HSeO}}_{4}^{-}[/latex]
- NH3 or H2O
- PH3 or HI
- NH3 or PH3
- H2S or HBr
- Rank the compounds in each of the following groups in order of increasing acidity or basicity, as indicated, and explain the order you assign.
- acidity: HCl, HBr, HI
- basicity: H2O, OH−, H−, Cl−
- basicity: Mg(OH)2, Si(OH)4, ClO3(OH) (Hint: Formula could also be written as HClO4).
- acidity: HF, H2O, NH3, CH4
- Rank the compounds in each of the following groups in order of increasing acidity or basicity, as indicated, and explain the order you assign.
- acidity: NaHSO3, NaHSeO3, NaHSO4
- basicity: [latex]{\text{BrO}}_{2}^{-}[/latex], [latex]{\text{ClO}}_{2}^{-}[/latex], [latex]{\text{IO}}_{2}^{-}[/latex]
- acidity: HOCl, HOBr, HOI
- acidity: HOCl, HOClO, HOClO2, HOClO3
- basicity: [latex]{\text{NH}}_{2}^{-}[/latex], HS−, HTe−, [latex]{\text{PH}}_{2}^{-}[/latex]
- basicity: BrO−, [latex]{\text{BrO}}_{2}^{-}[/latex], [latex]{\text{BrO}}_{3}^{-}[/latex], [latex]{\text{BrO}}_{4}^{-}[/latex]
- The active ingredient formed by aspirin in the body is salicylic acid, C6H4OH(CO2H). The carboxyl group (−CO2H) acts as a weak acid. The phenol group (an OH group bonded to an aromatic ring) also acts as an acid but a much weaker acid. List, in order of descending concentration, all of the ionic and molecular species present in a 0.001-M aqueous solution of C6H4OH(CO2H).
Show Solution
- [H2O] > [CH3CO2H] > [latex]\left[{\text{H}}_{3}{\text{O}}^{+}\right][/latex] ≈ [latex]\left[{\text{CH}}_{3}{\text{CO}}_{2}^{-}\right][/latex] > [OH−]
- The strongest base or strongest acid is the one with the larger Kb or Ka, respectively. In these two examples, they are (CH3)2NH and [latex]{\text{CH}}_{3}{\text{NH}}_{3}^{+}[/latex].
- Look up Ionization Constants of Weak Bases the value of Kb for (CH3)3N and the value of Ka for H3BO3. From the latter, calculate the value of Kb for [latex]{\text{H}}_{2}{\text{BO}}_{3}^{-}[/latex]. Then compare values:
- Kb(CH3)3N = 7.4 × 10−5
- [latex]{K}_{\text{a}}\left({\text{H}}_{3}{\text{BO}}_{3}\right)=5.8\times {10}^{-10}=\frac{{K}_{\text{w}}}{{K}_{\text{b}}}[/latex], [latex]{K}_{\text{b}}=\frac{1.0\times {10}^{-14}}{5.8\times {10}^{-10}}=1.7\times {10}^{-5}[/latex]
- A comparison shows that the larger Kb is that of triethylamine.
- The more acidic compounds are as follows:
- [latex]{\text{HSO}}_{4}^{-}[/latex]; higher electronegativity of the central ion.
- H2O; NH3 is a base and water is neutral, or decide on the basis of Ka values.
- HI; PH3 is weaker than HCl; HCl is weaker than HI. Thus, PH3 is weaker than HI.
- PH3; in binary compounds of hydrogen with nonmetals, the acidity increases for the element lower in a group.
- HBr; in a period, the acidity increases from left to right; in a group, it increases from top to bottom. Br is to the left and below S, so HBr is the stronger acid.
- The correct ordered lists are as follows:
- NaHSeO3 < NaHSO3 < NaHSO4; in polyoxy acids, the more electronegative central element—S, in this case—forms the stronger acid. The larger number of oxygen atoms on the central atom (giving it a higher oxidation state) also creates a greater release of hydrogen atoms, resulting in a stronger acid. As a salt, the acidity increases in the same manner.
- [latex]{\text{ClO}}_{2}^{-}<{\text{BrO}}_{2}^{-}<{\text{IO}}_{2}^{-}[/latex]; the basicity of the anions in a series of acids will be the opposite of the acidity in their oxyacids. The acidity increases as the electronegativity of the central atom increases. Cl is more electronegative than Br, and I is the least electronegative of the three.
- HOI < HOBr < HOCl; in a series of the same form of oxyacids, the acidity increases as the electronegativity of the central atom increases. Cl is more electronegative than Br, and I is the least electronegative of the three.
- HOCl < HOClO < HOClO2 < HOClO3; in a series of oxyacids of the same central element, the acidity increases as the number of oxygen atoms increases (or as the oxidation state of the central atom increases).
- [latex]{\text{HTe}}^{-}<{\text{HS}}^{-}<<{\text{PH}}_{2}^{-}<{\text{NH}}_{2}^{-}[/latex]; [latex]{\text{PH}}_{2}^{-}[/latex] and [latex]{\text{NH}}_{2}^{-}[/latex] are anions of weak bases, so they act as strong bases toward H+. [latex]{\text{HTe}}^{-}[/latex] and HS− are anions of weak acids, so they have less basic character. In a periodic group, the more electronegative element has the more basic anion.
- [latex]{\text{BrO}}_{4}^{-}<{\text{BrO}}_{3}^{-}<{\text{BrO}}_{2}^{-}<{\text{BrO}}^{-}[/latex]; with a larger number of oxygen atoms (that is, as the oxidation state of the central ion increases), the corresponding acid becomes more acidic and the anion consequently less basic.
- [latex]\left[\text{H}_{2}\text{O}\right]\gt\left[\text{C}_{6}\text{H}_{4}\text{OH}\left(\text{CO}_{2}\text{H}\right)\right]\gt\left[\text{H}^{+}\right]\text{O}\gt\left[\text{C}_{6}\text{H}_{4}\text{OH}\left(\text{CO}_{2}\right)^{-}\right]\gt\left[\text{C}_{6}\text{H}_{4}\text{O}\left(\text{CO}_{2}\text{H}\right)^{-}\right]\gt\left[\text{OH}^{-}\right][/latex]
Try It
- Nitric acid reacts with insoluble copper(II) oxide to form soluble copper(II) nitrate, Cu(NO3)2, a compound that has been used to prevent the growth of algae in swimming pools. Write the balanced chemical equation for the reaction of an aqueous solution of HNO3 with CuO.
- Gastric juice, the digestive fluid produced in the stomach, contains hydrochloric acid, HCl. Milk of Magnesia, a suspension of solid Mg(OH)2 in an aqueous medium, is sometimes used to neutralize excess stomach acid. Write a complete balanced equation for the neutralization reaction, and identify the conjugate acid-base pairs
- What do we represent when we write: [latex]{\text{CH}}_{3}{\text{CO}}_{2}\text{H}\left(aq\right)+{\text{H}}_{2}\text{O}\left(l\right)\rightleftharpoons {\text{H}}_{3}{\text{O}}^{+}\left(aq\right)+{\text{CH}}_{3}{\text{CO}}_{2}^{-}\left(aq\right)?[/latex]
- Explain why equilibrium calculations are not necessary to determine ionic concentrations in solutions of certain strong electrolytes such as NaOH and HCl. Under what conditions are equilibrium calculations necessary as part of the determination of the concentrations of all ions of some other strong electrolytes in solution?
- Are the concentrations of hydronium ion and hydroxide ion in a solution of an acid or a base in water directly proportional or inversely proportional? Explain your answer.
- What two common assumptions can simplify calculation of equilibrium concentrations in a solution of a weak acid?
- What two common assumptions can simplify calculation of equilibrium concentrations in a solution of a weak base?
Show Selected Solutions
- [latex]\begin{array}{cccccc}\text{Mg}{\left(\text{OH}\right)}_{2}\left(s\right)+& \text{HCl}\left(aq\right)& \longrightarrow & {\text{Mg}}^{2+}\left(aq\right)+& 2{\text{Cl}}^{-}\left(aq\right)+& {\text{2H}}_{2}\text{O}\left(l\right)\\ \text{BB}& \text{BA}& & \text{CB}& \text{CA}& \end{array}[/latex]
- Strong electrolytes are 100% ionized, and, as long as the component ions are neither weak acids nor weak bases, the ionic species present result from the dissociation of the strong electrolyte. Equilibrium calculations are necessary when one (or more) of the ions is a weak acid or a weak base.
- The two assumptions are
- Assume that the change in initial concentration of the acid as the equilibrium is established can be neglected, so this concentration can be assumed constant and equal to the initial value of the total acid concentration.
- Assume we can neglect the contribution of water to the equilibrium concentration of [latex]{\text{H}}_{3}{\text{O}}^{+}[/latex].
Try It
- Which of the following will increase the percent of NH3 that is converted to the ammonium ion in water (Hint: Use LeChâtelier’s principle.)?
- addition of NaOH
- addition of HCl
- addition of NH4Cl
- Which of the following will increase the percent of HF that is converted to the fluoride ion in water?
- addition of NaOH
- addition of HCl
- addition of NaF
- What is the effect on the concentrations of [latex]{\text{NO}}_{2}^{-}[/latex], HNO2, and OH− when the following are added to a solution of KNO2 in water:
- HCl
- HNO2
- NaOH
- NaCl
- KNO
The equation for the equilibrium is: [latex]{\text{NO}}_{2}^{-}\left(aq\right)+{\text{H}}_{2}\text{O}\left(l\right)\rightleftharpoons {\text{HNO}}_{2}\left(aq\right)+{\text{OH}}^{-}\left(aq\right)[/latex]
- What is the effect on the concentration of hydrofluoric acid, hydronium ion, and fluoride ion when the following are added to separate solutions of hydrofluoric acid?
- HCl
- KF
- NaCl
- KOH
- HF
The equation for the equilibrium is: [latex]\text{HF}\left(aq\right)+{\text{H}}_{2}\text{O}\left(l\right)\rightleftharpoons {\text{H}}_{3}{\text{O}}^{+}\left(aq\right)+{\text{F}}^{-}\left(aq\right)[/latex]
- Why is the hydronium ion concentration in a solution that is 0.10 M in HCl and 0.10 M in HCOOH determined by the concentration of HCl?
- From the equilibrium concentrations given, calculate Ka for each of the weak acids and Kb for each of the weak bases.
- CH3CO2H: [latex]\left[{\text{H}}_{3}{\text{O}}^{+}\right][/latex] = 1.34 × 10−3M; [latex]\left[{\text{CH}}_{3}{\text{CO}}_{2}^{-}\right][/latex] = 1.34 × 10−3M; [CH3CO2H] = 9.866 × 10−2M
- ClO−: [OH−] = 4.0 × 10−4M; [HClO] = 2.38 × 10−5M; [ClO−] = 0.273 M
- HCO2H: [HCO2H] = 0.524 M; [latex]\left[{\text{H}}_{3}{\text{O}}^{+}\right][/latex] = 9.8 × 10−3M; [latex]\left[{\text{HCO}}_{2}^{-}\right][/latex] = 9.8 × 10−3M
- [latex]{\text{C}}_{6}{\text{H}}_{5}{\text{NH}}_{3}^{+}:[/latex] [latex]\left[{\text{C}}_{6}{\text{H}}_{5}{\text{NH}}_{3}^{+}\right][/latex] = 0.233 M; [C6H5NH2] = 2.3 × 10−3M; [latex]\left[{\text{H}}_{3}{\text{O}}^{+}\right][/latex] = 2.3 × 10−3M
- From the equilibrium concentrations given, calculate Ka for each of the weak acids and Kb for each of the weak bases.
- NH3: [OH−] = 3.1 × 10−3M; [latex]\left[{\text{NH}}_{4}^{+}\right][/latex] = 3.1 × 10−3M; [NH3] = 0.533 M
- HNO2: [latex]\left[{\text{H}}_{3}{\text{O}}^{+}\right][/latex] = 0.011 M; [latex]\left[{\text{NO}}_{2}^{-}\right][/latex] = 0.0438 M; [HNO2] = 1.07 M
- (CH3)3N: [(CH3)3N] = 0.25 M; [latex]\left[{\left({\text{CH}}_{3}\right)}_{3}{\text{NH}}^{+}\right][/latex] = 4.3 × 10−3M; [OH−] = 4.3 × 10−3M
- [latex]{\text{NH}}_{4}^{+}:[/latex] [latex]\left[{\text{NH}}_{4}^{+}\right][/latex] = 0.100 M; [NH3] = 7.5 × 10−6M; [latex]\left[{\text{H}}_{3}{\text{O}}^{+}\right][/latex] = 7.5 × 10−6M
- Determine Kb for the nitrite ion, [latex]{\text{NO}}_{2}^{-}[/latex]. In a 0.10-M solution this base is 0.0015% ionized.
- Determine Ka for hydrogen sulfate ion, [latex]{\text{HSO}}_{4}^{-}[/latex]. In a 0.10-M solution the acid is 29% ionized.
- Calculate the ionization constant for each of the following acids or bases from the ionization constant of its conjugate base or conjugate acid:
- F−
- [latex]{\text{NH}}_{4}^{+}[/latex]
- [latex]{\text{AsO}}_{4}^{3-}[/latex]
- [latex]{\left({\text{CH}}_{3}\right)}_{2}{\text{NH}}_{2}^{+}[/latex]
- [latex]{\text{NO}}_{2}^{-}[/latex]
- [latex]{\text{HC}}_{2}{\text{O}}_{4}^{-}[/latex] (as a base)
- Calculate the ionization constant for each of the following acids or bases from the ionization constant of its conjugate base or conjugate acid:
- HTe− (as a base)
- [latex]{\left({\text{CH}}_{3}\right)}_{3}{\text{NH}}^{+}[/latex]
- [latex]{\text{HAsO}}_{4}^{3-}[/latex] (as a base)
- [latex]{\text{HO}}_{2}^{-}[/latex] (as a base)
- [latex]{\text{C}}_{6}{\text{H}}_{5}{\text{NH}}_{3}^{+}[/latex]
- [latex]{\text{HSO}}_{3}^{-}[/latex] (as a base)
- For which of the following solutions must we consider the ionization of water when calculating the pH or pOH?
- 3 × 10−8M HNO3
- 0.10 g HCl in 1.0 L of solution
- 0.00080 g NaOH in 0.50 L of solution
- 1 × 10−7M Ca(OH)2
- 0.0245 M KNO3
- Even though both NH3 and C6H5NH2 are weak bases, NH3 is a much stronger acid than C6H5NH2. Which of the following is correct at equilibrium for a solution that is initially 0.10 M in NH3 and 0.10 M in C6H5NH2?
- [latex]\left[{\text{OH}}^{-}\right]=\left[{\text{NH}}_{4}^{+}\right][/latex]
- [latex]\left[{\text{NH}}_{4}^{+}\right]=\left[{\text{C}}_{6}{\text{H}}_{5}{\text{NH}}_{3}^{+}\right][/latex]
- [latex]\left[{\text{OH}}^{-}\right]=\left[{\text{C}}_{6}{\text{H}}_{5}{\text{NH}}_{3}^{+}\right][/latex]
- [NH3] = [C6H5NH2]
- both a and b are correct
Show Selected Solutions
- The equilibrium is [latex]{\text{NH}}_{3}\left(aq\right)+{\text{H}}_{2}\text{O}\left(l\right)\rightleftharpoons {\text{NH}}_{4}^{+}\left(aq\right)+{\text{OH}}^{-}\left(aq\right)[/latex]
- The addition of NaOH adds OH− to the system and, according to Le Châtelier’s principle, the equilibrium will shift to the left. Thus, the percent of converted NH3 will decrease.
- The addition of HCl will add [latex]{\text{H}}_{3}{\text{O}}^{+}[/latex] ions, which will then react with the OH− ions. Thus, the equilibrium will shift to the right, and the percent will increase.
- The addition of NH4Cl adds [latex]{\text{NH}}_{4}^{+}[/latex] ions, shifting the equilibrium to the left. Thus, the percent will decrease.
- The effects are as follows:
- Adding HCl will add [latex]{\text{H}}_{3}{\text{O}}^{+}[/latex] ions, which will then react with the OH− ions, lowering their concentration. The equilibrium will shift to the right, increasing the concentration of HNO2, and decreasing the concentration of [latex]{\text{NO}}_{2}^{-}[/latex] ions.
- Adding HNO2 increases the concentration of HNO2 and shifts the equilibrium to the left, increasing the concentration of [latex]{\text{NO}}_{2}^{-}[/latex] ions and decreasing the concentration of OH− ions.
- Adding NaOH adds OH− ions, which shifts the equilibrium to the left, increasing the concentration of [latex]{\text{NO}}_{2}^{-}[/latex] ions and decreasing the concentrations of HNO2.
- Adding NaCl has no effect on the concentrations of the ions.
- Adding KNO2 adds [latex]{\text{NO}}_{2}^{-}[/latex] ions and shifts the equilibrium to the right, increasing the HNO2 and OH− ion concentrations.
- The equations of the occurring chemical processes are:
- [latex]\text{HCl}\left(aq\right)+{\text{H}}_{2}\text{O}\left(l\right)\longrightarrow {\text{H}}_{3}{\text{O}}^{+}\left(aq\right)+{\text{Cl}}^{-}\left(aq\right)[/latex]
- [latex]{\text{CH}}_{3}\text{COOH}\left(aq\right)+{\text{H}}_{2}\text{O}\left(l\right)\rightleftharpoons {\text{H}}_{3}{\text{O}}^{+}\left(aq\right)+{\text{CH}}_{3}{\text{COO}}^{-}\left(aq\right)[/latex]
- This is a case in which the solution contains a mixture of acids of different ionization strengths. In solution, the HCO2H exists primarily as HCO2H molecules because the ionization of the weak acid is suppressed by the strong acid. Therefore, the HCO2H contributes a negligible amount of hydronium ions to the solution. The stronger acid, HCl, is the dominant producer of hydronium ions because it is completely ionized. In such a solution, the stronger acid determines the concentration of hydronium ions, and the ionization of the weaker acid is fixed by the [latex]\left[{\text{H}}_{3}{\text{O}}^{+}\right][/latex] produced by the stronger acid.
- Ka and Kb are as follows:
- The reaction is [latex]{\text{NH}}_{3}\left(aq\right)+{\text{H}}_{2}\text{O}\left(l\right)\rightleftharpoons {\text{OH}}^{-}\left(aq\right)+{\text{NH}}_{4}^{+}\left(aq\right)[/latex]
[latex]{K}_{\text{b}}=\frac{\left[{\text{NH}}_{4}^{+}\right]\left[{\text{OH}}^{-}\right]}{\left[{\text{NH}}_{3}\right]}=\frac{\left(3.1\times {10}^{-3}\right)\left(3.1\times {10}^{-3}\right)}{\left(0.533\right)}=1.8\times {10}^{-5}[/latex] - The reaction is [latex]{\text{HNO}}_{2}\left(aq\right)+{\text{H}}_{2}\text{O}\left(l\right)\rightleftharpoons {\text{H}}_{3}{\text{O}}^{+}\left(aq\right)+{\text{NO}}_{2}^{-}\left(aq\right)[/latex]
[latex]{K}_{\text{a}}=\frac{\left[{\text{NO}}_{2}^{-}\right]\left[{\text{H}}_{3}{\text{O}}^{+}\right]}{\left[{\text{HNO}}_{2}\right]}=\frac{\left(0.0438\right)\left(0.011\right)}{\left(1.07\right)}=4.5\times {10}^{-4}[/latex] - The reaction is [latex]{\left({\text{CH}}_{3}\right)}_{3}\text{N}\left(aq\right)+{\text{H}}_{2}\text{O}\left(l\right)\rightleftharpoons {\text{OH}}^{-}\left(aq\right)+{\left({\text{CH}}_{3}\right)}_{3}{\text{NH}}^{+}\left(aq\right)[/latex]
[latex]{K}_{\text{b}}=\frac{\left[{\left({\text{CH}}_{3}\right)}_{3}{\text{NH}}^{+}\right]\left[{\text{OH}}^{-}\right]}{\left[{\left({\text{CH}}_{3}\right)}_{3}\text{N}\right]}=\frac{\left(4.3\times {10}^{-3}\right)\left(4.3\times {10}^{-3}\right)}{\left(0.25\right)}=7.4\times {10}^{-5}[/latex] - The reaction is [latex]{\text{NH}}_{4}^{+}\left(aq\right)+{\text{H}}_{2}\text{O}\left(l\right)\rightleftharpoons {\text{H}}_{3}{\text{O}}^{+}\left(aq\right)+{\text{NH}}_{3}\left(aq\right)[/latex]
[latex]{K}_{\text{a}}=\frac{\left[{\text{NH}}_{3}\right]\left[{\text{H}}_{3}{\text{O}}^{+}\right]}{\left[{\text{NH}}_{4}^{+}\right]}=\frac{\left(7.5\times {10}^{-6}\right)\left(7.5\times {10}^{-6}\right)}{\left(0.100\right)}=5.6\times {10}^{-10}[/latex]
- The reaction is [latex]{\text{NH}}_{3}\left(aq\right)+{\text{H}}_{2}\text{O}\left(l\right)\rightleftharpoons {\text{OH}}^{-}\left(aq\right)+{\text{NH}}_{4}^{+}\left(aq\right)[/latex]
- The reaction is [latex]{\text{HSO}}_{4}^{-}\left(aq\right)+{\text{H}}_{2}\text{O}\left(l\right)\rightleftharpoons {\text{H}}_{3}{\text{O}}^{+}\left(aq\right)+{\text{SO}}_{4}^{2-}\left(aq\right)[/latex].
- The concentrations at equilibrium are:
- [latex]\left[{\text{H}}_{3}{\text{O}}^{+}\right][/latex] = [latex]\left[{\text{SO}}_{4}^{2-}\right][/latex] = (0.29)(0.10 M) = 0.029 M
- [latex]\left[{\text{HSO}}_{4}^{-}\right][/latex] = 0.10 M − 0.029 M = 0.071 M
- [latex]{K}_{\text{a}}=\frac{\left[{\text{SO}}_{4}^{2-}\right]\left[{\text{H}}_{3}{\text{O}}^{+}\right]}{\left[{\text{HSO}}_{4}^{-}\right]}=\frac{\left(0.029\right)\left(0.029\right)}{\left(0.071\right)}=1.2\times {10}^{-2}[/latex]
- The ionization constants are as follows:
- [latex]{K}_{\text{b}}=\frac{{K}_{\text{w}}}{{K}_{\text{a}}}=\frac{\left(1.00\times {10}^{-14}\right)}{2.3\times {10}^{-3}}=4.3\times {10}^{-12}[/latex]
- [latex]{K}_{\text{a}}=\frac{{K}_{\text{w}}}{{K}_{\text{b}}}=\frac{\left(1.00\times {10}^{-14}\right)}{7.4\times {10}^{-5}}=1.4\times {10}^{-10}[/latex]
- [latex]{K}_{\text{b}}=\frac{{K}_{\text{w}}}{{K}_{\text{a}}}=\frac{\left(1.00\times {10}^{-14}\right)}{1\times {10}^{-7}}=1\times {10}^{-7}[/latex]
- [latex]{K}_{\text{b}}=\frac{{K}_{\text{w}}}{{K}_{\text{a}}}=\frac{\left(1.00\times {10}^{-14}\right)}{2.4\times {10}^{-12}}=4.2\times {10}^{-3}[/latex]
- [latex]{K}_{\text{b}}=\frac{{K}_{\text{w}}}{{K}_{\text{a}}}=\frac{\left(1.00\times {10}^{-14}\right)}{2.4\times {10}^{-12}}=4.2\times {10}^{-3}[/latex]
- [latex]{K}_{\text{b}}=\frac{{K}_{\text{w}}}{{K}_{\text{a}}}=\frac{\left(1.00\times {10}^{-14}\right)}{1.2\times {10}^{-2}}=8.3\times {10}^{-13}[/latex]
- The reactions are:
- [latex]\begin{array}{l}{\text{NH}}_{3}\left(aq\right)+{\text{H}}_{2}\text{O}\left(l\right)\rightleftharpoons {\text{NH}}_{4}^{+}\left(aq\right)+{\text{OH}}^{-}\left(aq\right)\\ {\text{C}}_{6}{\text{H}}_{5}{\text{NH}}_{2}\left(aq\right)+{\text{H}}_{2}\text{O}\left(l\right)\rightleftharpoons {\text{C}}_{6}{\text{H}}_{5}{\text{NH}}_{3}^{+}\left(aq\right)+{\text{OH}}^{-}\left(aq\right)\end{array}[/latex]
- Because NH3 is much stronger than C6H5NH2, it dissociates more. As the initial concentrations of both bases are the same, at equilibrium, [NH3] < [C6H5NH2], [latex]\left[{\text{NH}}_{4}^{+}\right][/latex] > [latex]\left[{\text{C}}_{6}{\text{H}}_{5}{\text{NH}}_{3}^{+}\right][/latex], and [OH−] > [latex]\left[{\text{C}}_{6}{\text{H}}_{5}{\text{NH}}_{3}^{+}\right][/latex]. Therefore, (a) is the correct statement. The contribution to the total [OH−] at equilibrium from C6H5NH2 is negligible compared to HN3. Therefore [latex]\left[{\text{OH}}^{-}\right]=\left[{\text{NH}}_{4}^{+}\right][/latex].
Glossary
acid ionization constant (Ka): equilibrium constant for the ionization of a weak acid
base ionization constant (Kb): equilibrium constant for the ionization of a weak base
leveling effect of water: any acid stronger than [latex]{\text{H}}_{3}{\text{O}}^{+}[/latex], or any base stronger than OH− will react with water to form [latex]{\text{H}}_{3}{\text{O}}^{+}[/latex], or OH−, respectively; water acts as a base to make all strong acids appear equally strong, and it acts as an acid to make all strong bases appear equally strong
oxyacid: compound containing a nonmetal and one or more hydroxyl groups
percent ionization: ratio of the concentration of the ionized acid to the initial acid concentration, times 100
Licenses and Attributions (Click to expand)
CC licensed content, Shared previously
- Chemistry 2e. Provided by: OpenStax. Located at: https://openstax.org/. License: CC BY: Attribution. License Terms: Access for free at
https://openstax.org/books/chemistry-2e/pages/1-introduction
All rights reserved content
- Acids and Bases Chemistry - Basic Introduction. Authored by: The Organic Chemistry Tutor. Located at: https://youtu.be/ZNo6gfCAgWE. License: Other. License Terms: Standard YouTube License
equilibrium constant for the ionization of a weak acid
ratio of the concentration of the ionized acid to the initial acid concentration, times 100
equilibrium constant for the ionization of a weak base
equilibrium constant for the ionization of a weak base
any acid stronger than [latex]{\text{H}}_{3}{\text{O}}^{+}[/latex], or any base stronger than OH− will react with water to form [latex]{\text{H}}_{3}{\text{O}}^{+}[/latex], or OH−, respectively; water acts as a base to make all strong acids appear equally strong, and it acts as an acid to make all strong bases appear equally strong
compound containing a nonmetal and one or more hydroxyl groups

