Chapter 5: Molecules, Compounds, and Chemical Equations

5.5 Formula mass

Learning Outcomes

  • Calculate formula masses for covalent and ionic compounds
  • Define the amount unit mole and the related quantity Avogadro’s number
  • Explain the relation between mass, moles, and numbers of atoms or molecules, and perform calculations deriving these quantities from one another

We can argue that modern chemical science began when scientists started exploring the quantitative as well as the qualitative aspects of chemistry. For example, Dalton’s atomic theory was an attempt to explain the results of measurements that allowed him to calculate the relative masses of elements combined in various compounds. Understanding the relationship between the masses of atoms and the chemical formulas of compounds allows us to quantitatively describe the composition of substances.

Formula Mass

Earlier, we described the development of the atomic mass unit, the concept of average atomic masses, and the use of chemical formulas to represent the elemental makeup of substances. These ideas can be extended to calculate the formula mass of a substance by summing the average atomic masses of all the atoms represented in the substance’s formula.

Molar Mass for Covalent Substances

Referring back to Chapter 2 we defined molar mass in respect to an element. The molar mass of an element is the mass in grams of 1 mole of that substance, a property expressed in units of grams per mole, which is equivalent to the atomic mass of that element. We can extend this concept to the molar mass of a compound, which is the mass in grams of 1 mole of that molecule or formula unit. The molar mass is calculated in the same was as the formula mass and are numerically equivalent.

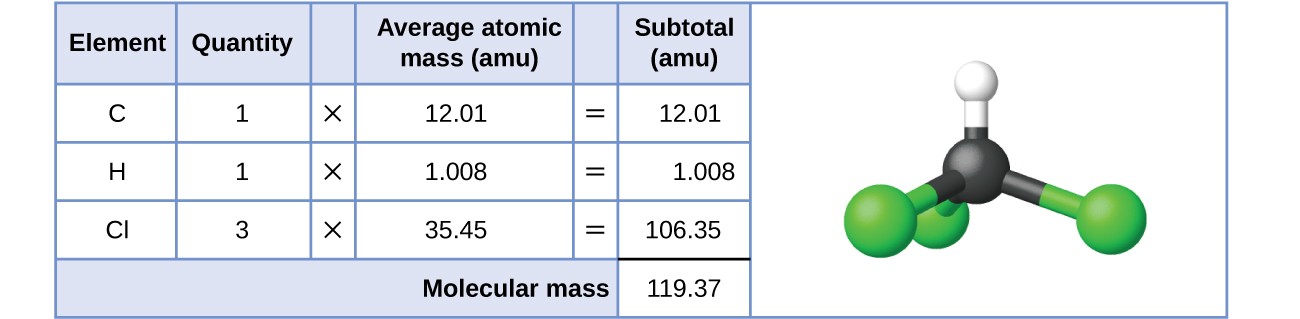
For covalent substances, the formula represents the numbers and types of atoms composing a single molecule of the substance; therefore, the formula mass may be correctly referred to as a molecular mass or molar mass. Consider chloroform ([latex]\ce{CHCl3}[/latex]), a covalent compound once used as a surgical anesthetic and now primarily used in the production of the “anti-stick” polymer, Teflon. The molecular formula of chloroform indicates that a single molecule contains one carbon atom, one hydrogen atom, and three chlorine atoms. The average molecular mass of a chloroform molecule is therefore equal to the sum of the average atomic masses of these atoms. Figure 5.5.1 outlines the calculations used to derive the molecular mass of chloroform, which is 119.37 amu.

A table and diagram are shown. The table is made up of six columns and five rows. The header row reads: “Element,” “Quantity,” a blank space, “Average atomic mass (a m u),” a blank space, and “Subtotal (a m u).” The first column contains the symbols “C,” “H,” “C l” and a blank, merged cell that runs the width of the first five columns. The second column contains the numbers “1,” “1,” and “3” as well as the merged cell. The third column contains the multiplication symbol in each cell except for the last, merged cell. The fourth column contains the numbers “12.01,” “1.008,” and “35.45” as well as the merged cell. The fifth column contains the symbol “=” in each cell except for the last, merged cell. The sixth column contains the values “12.01,” “1.008,” “106.35,” and “119.37.” There is a thick black line below the number 106.35. The merged cell under the first five columns reads “Molecular mass.” To the left of the table is a diagram of a molecule. Three green spheres are attached to a slightly smaller black sphere, which is also attached to a smaller white sphere. The green spheres lie beneath and to the sides of the black sphere while the white sphere is located straight up from the black sphere.
Figure 5.5.1. The average mass of a chloroform molecule, [latex]\ce{CHCl3}[/latex], is 119.37 amu, which is the sum of the average atomic masses of each of its constituent atoms. The black spheres represent carbon, white represents hydrogen, and green represents chlorine. The model shows the molecular structure of chloroform.

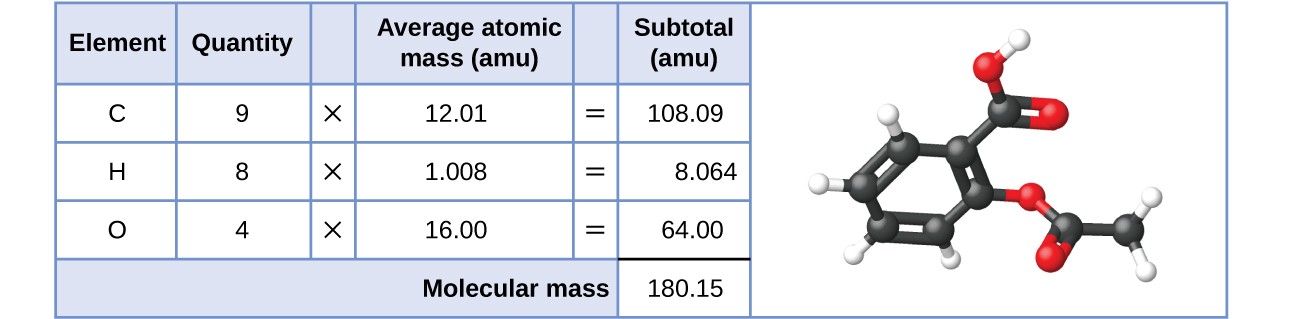
Likewise, the molecular mass of an aspirin molecule, [latex]\ce{C9H8O4}[/latex], is the sum of the atomic masses of nine carbon atoms, eight hydrogen atoms, and four oxygen atoms, which amounts to 180.15 amu (Figure 5.5.2).

A table and diagram are shown. The table is made up of six columns and five rows. The header row reads: “Element,” “Quantity,” a blank space, “Average atomic mass (a m u),” a blank space, and “Subtotal (a m u).” The first column contains the symbols “C,” “H,” “O,” and a merged cell. The merged cell runs the length of the first five columns. The second column contains the numbers “9,” “8,” and “4” as well as the merged, cell. The third column contains the multiplication symbol in each cell except for the last, merged cell. The fourth column contains the numbers “12.01,” “1.008,” and “16.00” as well as the merged cell. The fifth column contains the symbol “=” in each cell except for the last, merged cell. The sixth column contains the values: “108.09,” “8.064,” “64.00,” and “180.15.” There is a thick black line below the number 64.00. The merged cell under the first five columns reads “Molecular mass.” To the left of the table is a diagram of a molecule. Six black spheres are located in a six-sided ring and connected by alternating double and single black bonds. Attached to each of the four black spheres is one smaller white sphere. Attached to the farthest right black sphere is a red sphere, connected to two more black spheres, all in a row. Attached to the last black sphere of that row are two more white spheres. Attached to the first black sphere of that row is another red sphere. A black sphere, attached to two red spheres and a white sphere is attached to the black sphere on the top right of the six-sided ring.
Figure 5.5.2. The average mass of an aspirin molecule is 180.15 amu. The model shows the molecular structure of aspirin, [latex]\ce{C9H9O4}[/latex]. The black spheres represent carbon, white represents hydrogen, and red represents oxygen.

Example 5.5.1: Computing Molecular Mass for a Covalent Compound

Ibuprofen, [latex]\ce{C_{13}H_{18}O2}[/latex], is a covalent compound and the active ingredient in several popular nonprescription pain medications, such as Advil and Motrin. What is the molecular mass (amu) for this compound?

Show Solution

Molecules of this compound are comprised of 13 carbon atoms, 18 hydrogen atoms, and 2 oxygen atoms. Following the approach described above, the average molecular mass for this compound is therefore:
A table is shown that is made up of six columns and five rows. The header row reads: “Element,” “Quantity,” a blank space, “Average atomic mass (a m u),” a blank space, and “Subtotal (a m u).” The first column contains the symbols “C,” “H,” “O,” and a merged cell. The merged cell runs the length of the first five columns. The second column contains the numbers “13,” “8,” and “2” as well as the merged cell. The third column contains the multiplication symbol in each cell except for the last, merged cell. The fourth column contains the numbers “12.01,” “1.008,” and “16.00” as well as the merged cell. The fifth column contains the symbol “=” in each cell except for the last, merged cell. The sixth column contains the values “156.13,” “18.114,” “32.00,” and “206.27.” There is a thick black line below the number 32.00. The merged cell under the first five columns reads “Molecular mass.” To the right is a ball-and-stick model of the structure. At the center, it shows six black spheres arranged in a six-sided ring with alternating double bonds. The two black spheres at the top and bottom of the six-sided ring are each bonded to one, smaller, white sphere. The black sphere on the left side of the six-sided ring is connect to another black sphere. This sphere is connected to two smaller, white spheres and another black sphere. This black sphere is connected to one, smaller white sphere, and two other black spheres. Each of these last two black spheres is connected to two smaller, white spheres. The black sphere on the right side of the six-sided ring is connected to another black sphere. This black sphere is connected to one smaller, white sphere and two other black spheres. The black sphere that is connected to it and is situated to the top right is connected to two smaller, white spheres. The black sphere connected towards the bottom right is connected to two red spheres. It forms a double bond with one of these red spheres and the other red sphere is connected to a smaller, white sphere.

Check Your Learning

Formula Mass for Ionic Compounds

Ionic compounds are composed of discrete cations and anions combined in ratios to yield electrically neutral bulk matter. The formula mass for an ionic compound is calculated in the same way as the formula mass for covalent compounds: by summing the average atomic masses of all the atoms in the compound’s formula. Keep in mind, however, that the formula for an ionic compound does not represent the composition of a discrete molecule, so it is not correct to be referred to as the “molecular mass”. Keep in mind ionic compounds are not comprised of individual molecules so it is not correct to refer to the as molecules but is more appropriate to refer to them as a formula unit.

As an example, consider sodium chloride, [latex]\ce{NaCl}[/latex], the chemical name for common table salt. Sodium chloride is an ionic compound composed of sodium cations, [latex]\ce{Na+}[/latex], and chloride anions, [latex]\ce{Cl-}[/latex], combined in a 1:1 ratio. The formula mass for this compound is computed as 58.44 amu (see Figure 5.5.3).

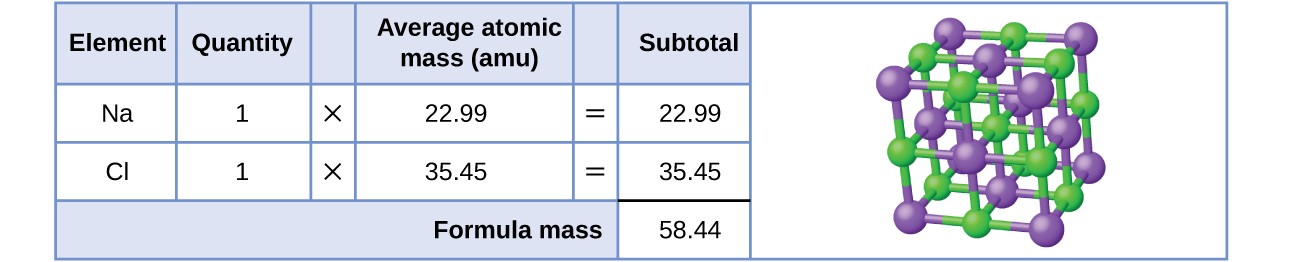
A table and diagram are shown. The table is made up of six columns and four rows. The header row reads: “Element,” “Quantity,” a blank space, “Average atomic mass (a m u),” a blank space and “Subtotal (a m u).” The first column contains the symbols “N a”, “C l,” and a merged cell. The merged cell runs the length of the first five columns. The second column contains the numbers “1” and “1” as well as the merged cell. The third column contains the multiplication symbol in each cell except for the last, merged cell. The fourth column contains the numbers “22.99” and “35.45” as well as the merged cell. The fifth column contains the symbol “=” in each cell except for the last, merged cell. The sixth column contains the values “22.99,” “35.45,” and “58.44.” There is a thick black line below the number “35.45.” The merged cell under the first five columns reads “Formula mass.” To the left of the table is a diagram of a chemical structure. The diagram shows green and purple spheres placed in an alternating pattern, making up the corners of eight stacked cubes to form one larger cube. The green spheres are slightly smaller than the purple spheres.
Figure 5.5.3. Table salt, NaCl, contains an array of sodium and chloride ions combined in a 1:1 ratio. Its formula mass is 58.44 amu.

Note that the average masses of neutral sodium and chlorine atoms were used in this computation, rather than the masses for sodium cations and chlorine anions. This approach is perfectly acceptable when computing the formula mass of an ionic compound. Even though a sodium cation has a slightly smaller mass than a sodium atom (since it is missing an electron), this difference will be offset by the fact that a chloride anion is slightly more massive than a chloride atom (due to the extra electron). Moreover, the mass of an electron is negligibly small with respect to the mass of a typical atom. Even when calculating the mass of an isolated ion, the missing or additional electrons can generally be ignored, since their contribution to the overall mass is negligible, reflected only in the nonsignificant digits that will be lost when the computed mass is properly rounded. The few exceptions to this guideline are very light ions derived from elements with precisely known atomic masses.

Example 5.5.2: Computing Formula Mass for an Ionic Compound

Aluminum sulfate, [latex]\ce{Al2(SO4)3}[/latex], is an ionic compound that is used in the manufacture of paper and in various water purification processes. What is the formula mass (amu) of this compound?

Show Solution

The formula for this compound indicates it contains [latex]\ce{Al^3+}[/latex] and [latex]\ce{SO4^2-}[/latex] ions combined in a 2:3 ratio. For purposes of computing a formula mass, it is helpful to rewrite the formula in the simpler format, [latex]\ce{Al2S3O_{12}}[/latex]. Following the approach outlined above, the formula mass for this compound is calculated as follows:

A table is shown that is made up of six columns and five rows. The header row reads: “Element,” “Quantity,” a blank space, “Average atomic mass (a m u),” a blank space, and “Subtotal (a m u).” The first column contains the symbols “A l,” “S,” “O,” and a merged cell. The merged cell runs the length of the first five columns. The second column contains the numbers “2,” “3,” and “12” as well as the merged cell. The third column contains the multiplication symbol in each cell except for the last, merged cell. The fourth column contains the numbers “26.98,” “32.06,” and “16.00” as well as the merged cell. The fifth column contains the symbol “=” in each cell except for the last, merged cell. The sixth column contains the values “53.96,” “96.18,” “192.00,” and “342.14.” There is a thick black line under the number 192.00. The merged cell under the first five columns reads “Molecular mass.” To the right of this table is a ball-and-stick structure. It shows yellow and grey sphere connected to red spheres in a complex pattern. The yellow and grey spheres are similar in size, but the red spheres appear to be smaller by comparison.

Check Your Learning

Molar Mass and mole conversion examples

Example 5.5.3: Deriving Moles from Grams for a Compound

Our bodies synthesize protein from amino acids. One of these amino acids is glycine, which has the molecular formula [latex]\ce{C2H5O2N}[/latex]. How many moles of glycine molecules are contained in 28.35 g of glycine?

Show Solution

We can derive the number of moles of a compound from its mass following the same procedure we used for an element in Example 5.5.3:
A diagram of two boxes connected by a right-facing arrow is shown. The box on the left contains the phrase, “Mass of C subscript 2 H subscript 5 O subscript 2 N ( g )” while the box on the right contains the phrase, “Moles of C subscript 2 H subscript 5 O subscript 2 N ( mol ).” There is a phrase under the arrow that says “Divide by molar mass (g / mol).”

The molar mass of glycine is required for this calculation, and it is computed in the same fashion as its molecular mass. One mole of glycine, [latex]\ce{C2H5O2N}[/latex], contains 2 moles of carbon, 5 moles of hydrogen, 2 moles of oxygen, and 1 mole of nitrogen:
A table is shown that is made up of six columns and six rows. The header row reads: “Element,” “Quantity (mol element / mol compound,” a blank space, “Molar mass (g / mol element),” a blank space, and “Subtotal (a m u).” The first column contains the symbols “C,” “H,” “O,” “N,” and a merged cell. The merged cell runs the width of the first five columns. The second column contains the numbers “2,” “5,” “2,” and “1” as well as the merged cell. The third column contains the multiplication symbol in each cell except for the last, merged cell. The fourth column contains the numbers “12.01,” “1.008,” “16.00,” and “14.007” as well as the merged cell. The fifth column contains the symbol “=” in each cell except for the last, merged cell. The sixth column contains the values “24.02,” “5.040,” “32.00,” “14.007,” and “75.07.” There is a thick black line under the number 14.007. The merged cell under the first five columns reads “Molar mass (g / mol compound). There is a ball-and-stick drawing to the right of this table. It shows a black sphere that forms a double bond with a slightly smaller red sphere, a single bond with another red sphere, and a single bond with another black sphere. The red sphere that forms a single bond with the black sphere also forms a single bond with a smaller, white sphere. The second black sphere forms a single bond with a smaller, white sphere and a smaller blue sphere. The blue sphere forms a single bond with two smaller, white spheres each.

The provided mass of glycine (~28 g) is a bit more than one-third the molar mass (~75 g/mol), so we would expect the computed result to be a bit greater than one-third of a mole (~0.33 mol). Dividing the compound’s mass by its molar mass yields:

[latex]28.35\cancel{\text{g}}\text{glycine}\left(\dfrac{\text{mol glycine}}{75.07\cancel{\text{g}}}\right)=0.378\text{ mol glycine}[/latex]

This result is consistent with our rough estimate.

Check Your Learning

Example 5.5.4: Deriving Grams from Moles for a Compound

Vitamin C has the molecular formula [latex]\ce{C6H8O6}[/latex]. The recommended daily dietary allowance of vitamin C for children aged 4–8 years is 1.42 × 10-4 mol. What is the mass of this allowance in grams?

Show Solution

As for elements, the mass of a compound can be derived from its molar amount as shown:
A diagram of two boxes connected by a right-facing arrow is shown. The box on the left contains the phrase, “Moles of vitamin C ( mol )” while the one the right contains the phrase, “Mass of vitamin C ( g )”. There is a phrase under the arrow that says “Multiply by molar mass (g / mol).”

The molar mass for this compound is computed to be 176.124 g/mol. The given number of moles is a very small fraction of a mole (~10-4 or one-ten thousandth); therefore, we would expect the corresponding mass to be about one-ten thousandth of the molar mass (~0.02 g). Performing the calculation, we get:

[latex]1.42\times {10}^{-4}\cancel{\text{mol}}\text{vitamin C}\left(\dfrac{176.124\text{g}}{\cancel{\text{mol}}\text{vitamin C}}\right)=0.0250\text{g vitamin C}[/latex]

This is consistent with the anticipated result.

Check Your Learning

Key Concepts and Summary

The formula mass of a substance is the sum of the average atomic masses of each atom represented in the chemical formula and is expressed in atomic mass units. The formula mass of a compound is also called the molecular mass. A convenient amount unit for expressing very large numbers of atoms or molecules is the mole. Experimental measurements have determined the number of entities composing 1 mole of substance to be 6.022 × 1023, a quantity called Avogadro’s number. The mass in grams of 1 mole of substance is its molar mass. Due to the use of the same reference substance in defining the atomic mass unit and the mole, the formula mass (amu) and molar mass (g/mol) for any substance are numerically equivalent (for example, one [latex]\ce{H2O}[/latex] molecule weighs approximately18 amu and 1 mole of [latex]\ce{H2O}[/latex] molecules weighs approximately 18 g).

Try It

  1. What is the total mass (amu) of carbon in each of the following molecules?
    1. [latex]\ce{CH4}[/latex]
    2. [latex]\ce{CHCl3}[/latex]
    3. [latex]\ce{C_{12}H_{10}O6}[/latex]
    4. [latex]\ce{CH3CH2CH2CH2CH3}[/latex]
  2. Calculate the molar mass of each of the following compounds:
    1. hydrogen fluoride, [latex]\ce{HF}[/latex]
    2. ammonia, [latex]\ce{NH3}[/latex]
    3. nitric acid, [latex]\ce{HNO3}[/latex]
    4. silver sulfate,[latex]\ce{ Ag2SO4}[/latex]
    5. boric acid, [latex]\ce{B(OH)3}[/latex]
  3. Determine the mass of each of the following:
    1. 2.345 mol [latex]\ce{LiCl}[/latex]
    2. 0.0872 mol acetylene, [latex]\ce{C2H2}[/latex]
    3. 3.3 × 10-2 mol [latex]\ce{Na2CO3}[/latex]
    4. 1.23 × 103 mol fructose, [latex]\ce{C6H_{12}O6}[/latex]
    5. 0.5758 mol [latex]\ce{FeSO4(H2O)7}[/latex]
  4. Which contains the greatest mass of oxygen: 0.75 mol of ethanol (C2H5OH), 0.60 mol of formic acid (HCO2H), or 1.0 mol of water (H2O)? Explain why.
Show Selected Solutions
  1. Each molecule has the following mass (amu) of carbon.
    1. [latex]1\times 12.01\text{ amu}=12.01\text{ amu}[/latex]
    2. [latex]1\times 12.01\text{ amu}=12.01\text{ amu}[/latex]
    3. [latex]12\times 12.01\text{ amu}=144.12\text{ amu}[/latex]
    4. [latex]5\times 12.01\text{ amu}=60.05\text{ amu}[/latex]
  2. Formic acid. Its formula has twice as many oxygen atoms as the other two compounds (one each). Therefore, 0.60 mol of formic acid would be equivalent to 1.20 mol of a compound containing a single oxygen atom.

Glossary

formula mass: sum of the average masses for all atoms represented in a chemical formula; for covalent compounds, this is also the molecular mass

Licenses and Attributions (Click to expand)

CC licensed content, Shared previously

definition

License

Icon for the Creative Commons Attribution-NonCommercial-ShareAlike 4.0 International License

Chemistry Fundamentals Copyright © by Dr. Julie Donnelly, Dr. Nicole Lapeyrouse, and Dr. Matthew Rex is licensed under a Creative Commons Attribution-NonCommercial-ShareAlike 4.0 International License, except where otherwise noted.

Share This Book