3.1 Electromagnetic Energy

A Collective Work

Chapter 3: The Quantum-Mechanical Model of the Atom

3.1 Electromagnetic Energy

Learning Outcomes

Explain the basic behavior of waves, including traveling waves and standing waves
Describe the wave nature of light
Use appropriate equations to calculate related light-wave properties such as frequency, wavelength, and energy
Distinguish between line and continuous emission spectra
Describe the particle nature of light
sdfsdf

The nature of light has been a subject of inquiry since antiquity. In the seventeenth century, Isaac Newton performed experiments with lenses and prisms and was able to demonstrate that white light consists of the individual colors of the rainbow combined together. Newton explained his optics findings in terms of a “corpuscular” view of light, in which light was composed of streams of extremely tiny particles travelling at high speeds according to Newton’s laws of motion. Others in the seventeenth century, such as Christiaan Huygens, had shown that optical phenomena such as reflection and refraction could be equally well explained in terms of light as waves travelling at high speed through a medium called “luminiferous aether” that was thought to permeate all space. Early in the nineteenth century, Thomas Young demonstrated that light passing through narrow, closely spaced slits produced interference patterns that could not be explained in terms of Newtonian particles but could be easily explained in terms of waves. Later in the nineteenth century, after James Clerk Maxwell developed his theory of electromagnetic radiation and showed that light was the visible part of a vast spectrum of electromagnetic waves, the particle view of light became thoroughly discredited. By the end of the nineteenth century, scientists viewed the physical universe as roughly comprising two separate domains: matter composed of particles moving according to Newton’s laws of motion, and electromagnetic radiation consisting of waves governed by Maxwell’s equations. Today, these domains are referred to as classical mechanics and classical electrodynamics (or classical electromagnetism). Although there were a few physical phenomena that could not be explained within this framework, scientists at that time were so confident of the overall soundness of this framework that they viewed these aberrations as puzzling paradoxes that would ultimately be resolved somehow within this framework. As we shall see, these paradoxes led to a contemporary framework that intimately connects particles and waves at a fundamental level called wave-particle duality, which has superseded the classical view.

Visible light and other forms of electromagnetic radiation play important roles in chemistry, since they can be used to infer the energies of electrons within atoms and molecules. Much of modern technology is based on electromagnetic radiation. For example, radio waves from a mobile phone, X-rays used by dentists, the energy used to cook food in your microwave, the radiant heat from red-hot objects, and the light from your television screen are forms of electromagnetic radiation that all exhibit wavelike behavior.

Waves

A wave is an oscillation or periodic movement that can transport energy from one point in space to another. Common examples of waves are all around us. Shaking the end of a rope transfers energy from your hand to the other end of the rope, dropping a pebble into a pond causes waves to ripple outward along the water’s surface, and the expansion of air that accompanies a lightning strike generates sound waves (thunder) that can travel outward for several miles. In each of these cases, kinetic energy is transferred through matter (the rope, water, or air) while the matter remains essentially in place. An insightful example of a wave occurs in sports stadiums when fans in a narrow region of seats rise simultaneously and stand with their arms raised up for a few seconds before sitting down again while the fans in neighboring sections likewise stand up and sit down in sequence. While this wave can quickly encircle a large stadium in a few seconds, none of the fans actually travel with the wave-they all stay in or above their seats.

Waves need not be restricted to travel through matter. As Maxwell showed, electromagnetic waves consist of an electric field oscillating in step with a perpendicular magnetic field, both of which are perpendicular to the direction of travel. These waves can travel through a vacuum at a constant speed of 2.998 × 10⁸ m/s, the speed of light (denoted by c).

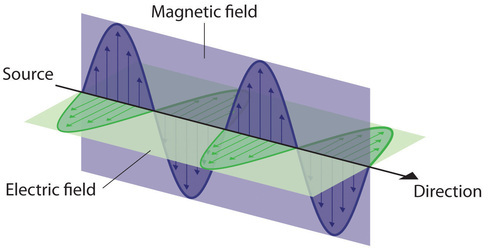
Figure 3.1.1: The Nature of Electromagnetic Radiation. All forms of electromagnetic radiation consist of perpendicular oscillating electric and magnetic fields.

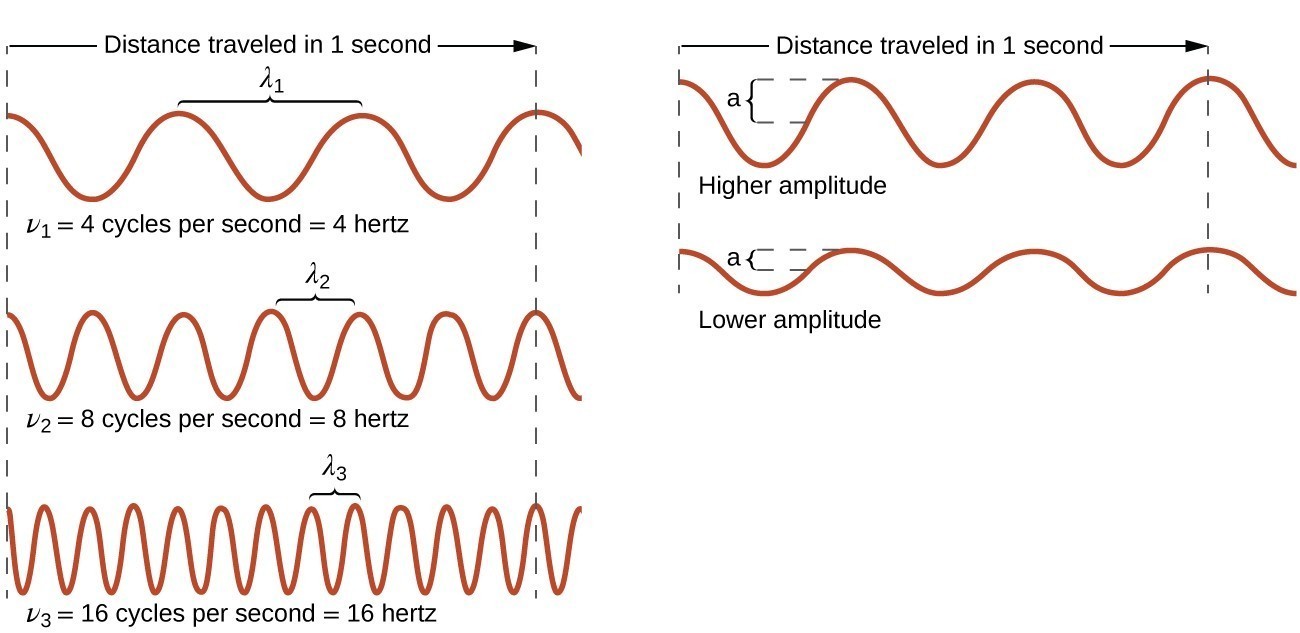
All waves, including forms of electromagnetic radiation, are characterized by a wavelength ([latex]\lambda[/latex]) [latex]\nu[/latex], the lowercase Greek letter nu), and an amplitude. As can be seen in Figure 3.1.1, the wavelength ([latex]\lambda[/latex]) is the distance between two consecutive peaks or troughs in a wave (measured in meters in the SI system). Electromagnetic waves have wavelengths that fall within an enormous range-wavelengths of kilometers (10³ m) to picometers (10^{[latex]-[/latex]12} m) have been observed. The frequency is the number of wave cycles that pass a specified point in space in a specified amount of time (in the SI system, this is measured in seconds). A cycle corresponds to one complete wavelength. The unit for frequency, expressed as cycles per second [s^{[latex]-[/latex]1}], is the hertz (Hz). Common multiples of this unit are megahertz, (1 MHz = 1 × 10⁶ Hz) and gigahertz (1 GHz = 1 × 10⁹ Hz). The amplitude corresponds to the magnitude of the wave’s displacement and so, in Figure 3.1.1, this corresponds to one-half the height between the peaks and troughs. The amplitude is related to the intensity of the wave, which for light is the brightness, and for sound is the loudness.

This figure includes 5 one-dimensional sinusoidal waves in two columns. The column on the left includes three waves, and the column on the right includes two waves. In each column, dashed vertical line segments extend down the left and right sides of the column. A right pointing arrow extends from the left dashed line to the right dashed line in both columns and is labeled, “Distance traveled in 1 second.” The waves all begin on the left side at a crest. The wave at the upper left shows 3 peaks to the right of the starting point. A bracket labeled, “lambda subscript 1,” extends upward from the second and third peaks. Beneath this wave is the label, “nu subscript 1 equals 4 cycles per second equals 4 hertz.” The wave below has six peaks to the right of the starting point with a bracket similarly connecting the third and fourth peaks which is labeled, “lambda subscript 2.” Beneath this wave is the label, “nu subscript 2 equals 8 cycles per second equals 8 hertz.” The third wave in the column has twelve peaks to the right of the starting point with a bracket similarly connecting the seventh and eighth peaks which is labeled, “lambda subscript 3.” Beneath this wave is the label, “nu subscript 3 equals 12 cycles per second equals 12 hertz.” All waves in this column appear to have the same vertical distance from peak to trough. In the second column, the two waves are similarly shown, but lack the lambda labels. The top wave in this column has a greater vertical distance between the peaks and troughs and is labeled, “Higher amplitude.” The wave beneath it has a lesser distance between the peaks and troughs and is labeled, “Lower amplitude.” — Figure 3.1.2 One-dimensional sinusoidal waves show the relationship among wavelength, frequency, and speed. The wave with the shortest wavelength has the highest frequency. Amplitude is one-half the height of the wave from peak to trough.

The product of a wave’s wavelength ([latex]\lambda[/latex]) and its frequency ([latex]\nu[/latex]), [latex]\lambda\nu[/latex], is the speed of the wave. Thus, for electromagnetic radiation in a vacuum, speed is equal to the fundamental constant, [latex]c[/latex]:

[latex]c=2.998\times {10}^{8}{\text{ms}}^{-1}=\lambda \nu[/latex]

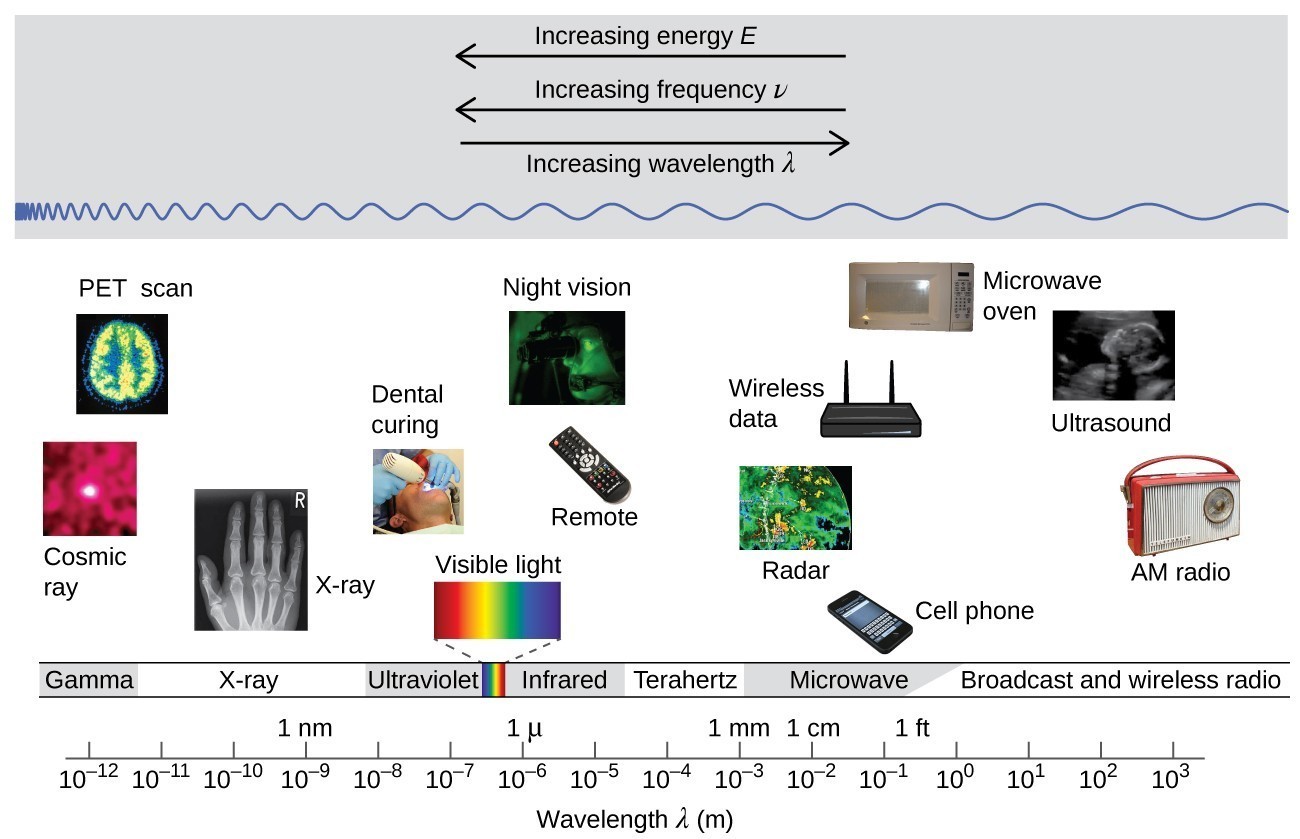
Wavelength and frequency are inversely proportional: As the wavelength increases, the frequency decreases. The inverse proportionality is illustrated in Figure 3.1.3. This figure also shows the electromagnetic spectrum, the range of all types of electromagnetic radiation. Each of the various colors of visible light has specific frequencies and wavelengths associated with them, and you can see that visible light makes up only a small portion of the electromagnetic spectrum. Because the technologies developed to work in various parts of the electromagnetic spectrum are different, for reasons of convenience and historical legacies, different units are typically used for different parts of the spectrum. For example, radio waves are usually specified as frequencies (typically in units of MHz), while the visible region is usually specified in wavelengths (typically in units of nm or angstroms).

The figure includes a portion of the electromagnetic spectrum which extends from gamma radiation at the far left through x-ray, ultraviolet, visible, infrared, terahertz, and microwave to broadcast and wireless radio at the far right. At the top of the figure, inside a grey box, are three arrows. The first points left and is labeled, “Increasing energy E.” A second arrow is placed just below the first which also points left and is labeled, “Increasing frequency nu.” A third arrow is placed just below which points right and is labeled, “Increasing wavelength lambda.” Inside the grey box near the bottom is a blue sinusoidal wave pattern that moves horizontally through the box. At the far left end, the waves are short and tightly packed. They gradually lengthen moving left to right across the figure, resulting in significantly longer waves at the right end of the diagram. Beneath the grey box are a variety of photos aligned above the names of the radiation types and a numerical scale that is labeled, “Wavelength lambda ( m ).” This scale runs from 10 superscript negative 12 meters under gamma radiation increasing by powers of ten to a value of 10 superscript 3 meters at the far right under broadcast and wireless radio. X-ray appears around 10 superscript negative 10 meters, ultraviolet appears in the 10 superscript negative 8 to 10 superscript negative 7 range, visible light appears between 10 superscript negative 7 and 10 superscript negative 6, infrared appears in the 10 superscript negative 6 to 10 superscript negative 5 range, teraherz appears in the 10 superscript negative 4 to 10 superscript negative 3 range, microwave infrared appears in the 10 superscript negative 2 to 10 superscript negative 1 range, and broadcast and wireless radio extend from 10 to 10 superscript 3 meters. Labels above the scale are placed to indicate 1 n m at 10 superscript negative 9 meters, 1 micron at 10 superscript negative 6 meters, 1 millimeter at 10 superscript negative 3 meters, 1 centimeter at 10 superscript negative 2 meters, and 1 foot between 10 superscript negative 1 meter and 10 superscript 0 meters. A variety of images are placed beneath the grey box and above the scale in the figure to provide examples of related applications that use the electromagnetic radiation in the range of the scale beneath each image. The photos on the left above gamma radiation show cosmic rays and a multicolor PET scan image of a brain. A black and white x-ray image of a hand appears above x-rays. An image of a patient undergoing dental work, with a blue light being directed into the patient's mouth is labeled, “dental curing,” and is shown above ultraviolet radiation. Between the ultraviolet and infrared labels is a narrow band of red, orange, yellow, green, blue, indigo, and violet colors in narrow, vertical strips. From this narrow band, two dashed lines extend a short distance above to the left and right of an image of the visible spectrum. The image, which is labeled, “visible light,” is just a broader version of the narrow bands of color in the label area. Above infrared are images of a television remote and a black and green night vision image. At the left end of the microwave region, a satellite radar image is shown. Just right of this and still above the microwave region are images of a cell phone, a wireless router that is labeled, “wireless data,” and a microwave oven. Above broadcast and wireless radio are two images. The left most image is a black and white medical ultrasound image. A wireless AM radio is positioned at the far right in the image, also above broadcast and wireless radio. — Figure 3.1.3 Portions of the electromagnetic spectrum are shown in order of decreasing frequency and increasing wavelength. Examples of some applications for various wavelengths include positron emission tomography (PET) scans, X-ray imaging, remote controls, wireless Internet, cellular telephones, and radios. (credit “Cosmic ray”: modification of work by NASA; credit “PET scan”: modification of work by the National Institute of Health; credit “X-ray”: modification of work by Dr. Jochen Lengerke; credit “Dental curing”: modification of work by the Department of the Navy; credit “Night vision”: modification of work by the Department of the Army; credit “Remote”: modification of work by Emilian Robert Vicol; credit “Cell phone”: modification of work by Brett Jordan; credit “Microwave oven”: modification of work by Billy Mabray; credit “Ultrasound”: modification of work by Jane Whitney; credit “AM radio”: modification of work by Dave Clausen)

Example 3.1.1: Determining the Frequency and Wavelength of Radiation

A sodium streetlight gives off yellow light that has a wavelength of 589 nm (1 nm = 1× 10^{[latex]-[/latex]9} m). What is the frequency of this light?

Show Solution

We can rearrange the equation c = [latex]\lambda\nu[/latex] to solve for the frequency: [latex]\nu =\frac{c}{\lambda }[/latex]

Since c is expressed in meters per second, we must also convert 589 nm to meters.

[latex]\nu =\left(\dfrac{2.998\times {10}^{8}\cancel{\text{m}}{\text{s}}^{-1}}{589\cancel{\text{nm}}}\right)\left(\dfrac{1\times {10}^{9}\cancel{\text{nm}}}{1\cancel{\text{m}}}\right)=5.09\times {10}^{14}{\text{s}}^{-1}[/latex]

Check Your Learning

One particularly characteristic phenomenon of waves results when two or more waves come into contact: They interfere with each other. Figure 3.1.4 shows the interference patterns that arise when light passes through narrow slits closely spaced about a wavelength apart. The fringe patterns produced depend on the wavelength, with the fringes being more closely spaced for shorter wavelength light passing through a given set of slits. When the light passes through the two slits, each slit effectively acts as a new source, resulting in two closely spaced waves coming into contact at the detector (the camera in this case). The dark regions in Figure 3.1.4 correspond to regions where the peaks for the wave from one slit happen to coincide with the troughs for the wave from the other slit (destructive interference), while the brightest regions correspond to the regions where the peaks for the two waves (or their two troughs) happen to coincide (constructive interference). Likewise, when two stones are tossed close together into a pond, interference patterns are visible in the interactions between the waves produced by the stones. Such interference patterns cannot be explained by particles moving according to the laws of classical mechanics.

This image shows interference patterns for light passing through a narrow slit. Four distinct colored bands are arranged from top to bottom. The top band shows white light, the second red, the third green, and the fourth is blue. Each band shows a central square of color with narrower vertically oriented bands extending left and right on a black background. — Figure 3.1.4 Interference fringe patterns are shown for light passing through two closely spaced, narrow slits. The spacing of the fringes depends on the wavelength, with the fringes being more closely spaced for the shorter-wavelength blue light. (credit: PASCO)

Dorothy Hodgkin

Because the wavelengths of X-rays (10-10,000 picometers [pm]) are comparable to the size of atoms, X-rays can be used to determine the structure of molecules. When a beam of X-rays is passed through molecules packed together in a crystal, the X-rays collide with the electrons and scatter. Constructive and destructive interference of these scattered X-rays creates a specific diffraction pattern. Calculating backward from this pattern, the positions of each of the atoms in the molecule can be determined very precisely. One of the pioneers who helped create this technology was Dorothy Crowfoot Hodgkin.

She was born in Cairo, Egypt, in 1910, where her British parents were studying archeology. Even as a young girl, she was fascinated with minerals and crystals. When she was a student at Oxford University, she began researching how X-ray crystallography could be used to determine the structure of biomolecules. She invented new techniques that allowed her and her students to determine the structures of vitamin [latex]\ce{B_{12}}[/latex], penicillin, and many other important molecules. Diabetes, a disease that affects 382 million people worldwide, involves the hormone insulin. Hodgkin began studying the structure of insulin in 1934, but it required several decades of advances in the field before she finally reported the structure in 1969. Understanding the structure has led to better understanding of the disease and treatment options.

Not all waves are travelling waves. Standing waves (also known as stationary waves) remain constrained within some region of space. As we shall see, standing waves play an important role in our understanding of the electronic structure of atoms and molecules. The simplest example of a standing wave is a one-dimensional wave associated with a vibrating string that is held fixed at its two end points. Although the string’s motion lies mostly within a plane, the wave itself is considered to be one dimensional, since it lies along the length of the string. The motion of string segments in a direction perpendicular to the string length generates the waves and so the amplitude of the waves is visible as the maximum displacement of the curves seen in Figure 3.1.5. The key observation from the figure is that only those waves having an integer number, n, of half-wavelengths between the end points can form. A system with fixed end points such as this restricts the number and type of the possible waveforms. This is an example of quantization, in which only discrete values from a more general set of continuous values of some property are observed. Another important observation is that the harmonic waves (those waves displaying more than one-half wavelength) all have one or more points between the two end points that are not in motion. These special points are nodes. The energies of the standing waves with a given amplitude in a vibrating string increase with the number of half-wavelengths n. Since the number of nodes is n [latex]-[/latex] 1, the energy can also be said to depend on the number of nodes, generally increasing as the number of nodes increases.

This figure shows four one-dimensional standing waves. The waves are shown in a tan color and are composed of curves to represent standing waves that can be generated using string. The first image at the top of the figure shows a single long wave with no nodes, or points where the string appears to cross between the endpoints at the left and right sides of the figure. The second diagram just below shows a single node at the center of the wave, which divides the wave into two identical halves to the left and right. The third diagram shows two nodes, dividing the image into three identical parts to the left, center, and right. Similarly, the last image at the bottom of the figure shows three nodes, dividing the image into four identical parts. — Figure 3.1.5 A vibrating string shows some one-dimensional standing waves. Since the two end points of the string are held fixed, only waves having an integer number of half-wavelengths can form. The points on the string between the end points that are not moving are called the nodes.

An example of two-dimensional standing waves is shown in Figure 3.1.6, which shows the vibrational patterns on a flat surface. Although the vibrational amplitudes cannot be seen like they could in the vibrating string, the nodes have been made visible by sprinkling the drum surface with a powder that collects on the areas of the surface that have minimal displacement. For one-dimensional standing waves, the nodes were points on the line, but for two-dimensional standing waves, the nodes are lines on the surface (for three-dimensional standing waves, the nodes are two-dimensional surfaces within the three-dimensional volume).

This figure includes four images. In each image, a brown circular platform has been sprinkled with a tan powder, yellow wires connect to a cylindrical base beneath the platform. To the right of the platform is a white box with a blue front which is labeled, “5.289 k H z Function Generator.” The image in the top left shows three distinct rings formed from the tan powder evenly spaced from the center of the platform, with the first ring very close to the center of the platform. The box reads, “2.434 k H z.” The image in the top right is similar except that the rings are closer together and the central ring has a significantly greater radius than in the first diagram. In this photo, the box reads, “3.986 k H z.” The image at the lower left is similar to the image in the upper left except that more of the powder is present, and 8 evenly-spaced radii are formed from the tan powder on the platform, making a web-like image. In this photo, the box reads, “5.289 k H z.” In the lower right of the figure, the image is similar to what is shown in the upper right except that four evenly spaced radii are shown composed of the tan powder on the platform. In this photo, the box reads, “5.670 K H z.” — Figure 3.1.6 Two-dimensional standing waves can be visualized on a vibrating surface. The surface has been sprinkled with a powder that collects near the nodal lines. There are two types of nodes visible: radial nodes (circles) and angular nodes (radii).

Key Concepts and Summary

Light and other forms of electromagnetic radiation move through a vacuum with a constant speed, c, of 2.998 × 10⁸ m s⁻¹. This radiation shows wavelike behavior, which can be characterized by a frequency, [latex]\nu[/latex], and a wavelength, [latex]\lambda[/latex], such that c = [latex]\lambda\nu[/latex]. Light is an example of a travelling wave. Other important wave phenomena include standing waves, periodic oscillations, and vibrations. Standing waves exhibit quantization, since their wavelengths are limited to discrete integer multiples of some characteristic lengths. Electromagnetic radiation that passes through two closely spaced narrow slits having dimensions roughly similar to the wavelength will show an interference pattern that is a result of constructive and destructive interference of the waves.

Key Equation

[latex]c = \lambda\nu[/latex]

Try It

An FM radio station found at 103.1 on the FM dial broadcasts at a frequency of 1.031 × 10⁸ s^{[latex]-[/latex]1} (103.1 MHz). What is the wavelength of these radio waves in meters?
A bright violet line occurs at 435.8 nm in the emission spectrum of mercury vapor. What amount of energy, in joules, must be released by an electron in a mercury atom to produce a photon of this light?
When rubidium ions are heated to a high temperature, two lines are observed in its line spectrum at wavelengths (a) 7.9 × 10^{[latex]-[/latex]7} m and (b) 4.2 × 10^{[latex]-[/latex]7} m. What are the frequencies of the two lines? What color do we see when we heat a rubidium compound?

Show Solutions

Glossary

amplitude: extent of the displacement caused by a wave (for sinusoidal waves, it is one-half the difference from the peak height to the trough depth, and the intensity is proportional to the square of the amplitude)

electromagnetic radiation: energy transmitted by waves that have an electric-field component and a magnetic-field component

electromagnetic spectrum: range of energies that electromagnetic radiation can comprise, including radio, microwaves, infrared, visible, ultraviolet, X-rays, and gamma rays; since electromagnetic radiation energy is proportional to the frequency and inversely proportional to the wavelength, the spectrum can also be specified by ranges of frequencies or wavelengths

frequency ([latex]\nu[/latex]): number of wave cycles (peaks or troughs) that pass a specified point in space per unit time

hertz (Hz): the unit of frequency, which is the number of cycles per second, s^{[latex]-[/latex]1}

intensity: property of wave-propagated energy related to the amplitude of the wave, such as brightness of light or loudness of sound

interference pattern: pattern typically consisting of alternating bright and dark fringes; it results from constructive and destructive interference of waves

node: any point of a standing wave with zero amplitude

quantization: occurring only in specific discrete values, not continuous

standing wave: (also, stationary wave) localized wave phenomenon characterized by discrete wavelengths determined by the boundary conditions used to generate the waves; standing waves are inherently quantized

wave: oscillation that can transport energy from one point to another in space

wavelength ([latex]\lambda[/latex]): distance between two consecutive peaks or troughs in a wave

Licenses and Attributions (Click to expand)

CC licensed content, Shared previously

Chemistry 2e. Provided by: OpenStax. Located at: https://openstax.org/. License: CC BY: Attribution. License Terms: Access for free at
https://openstax.org/books/chemistry-2e/pages/1-introduction

Outrageous acts of science. Standing wave in salt. Authored by: firescience13. Located at: https://youtu.be/gmBYKLyC6Q4. License: Other. License Terms: Standard YouTube License

License

Icon for the Creative Commons Attribution-NonCommercial-ShareAlike 4.0 International License

Chemistry Fundamentals Copyright © by Dr. Julie Donnelly, Dr. Nicole Lapeyrouse, and Dr. Matthew Rex is licensed under a Creative Commons Attribution-NonCommercial-ShareAlike 4.0 International License, except where otherwise noted.