Chapter 17: Electrochemistry

17.6 Electrolysis

Learning Outcomes

  • Describe the process of electrolysis
  • Compare the operation of electrolytic cells with that of galvanic cells
  • Perform stoichiometric calculations for electrolytic processes

Electrochemical cells in which spontaneous redox reactions take place (galvanic cells) have been the topic of discussion so far in this chapter. In these cells, electrical work is done by a redox system on its surroundings as electrons produced by the redox reaction are transferred through an external circuit. This final section of the chapter will address an alternative scenario in which an external circuit does work on a redox system by imposing a voltage sufficient to drive an otherwise nonspontaneous reaction, a process known as electrolysis. A familiar example of electrolysis is recharging a battery, which involves use of an external power source to drive the spontaneous (discharge) cell reaction in the reverse direction, restoring to some extent the composition of the half-cells and the voltage of the battery. Perhaps less familiar is the use of electrolysis in the refinement of metallic ores, the manufacture of commodity chemicals, and the electroplating of metallic coatings on various products (e.g., jewelry, utensils, auto parts). To illustrate the essential concepts of electrolysis, a few specific processes will be considered.

The Electrolysis of Molten Sodium Chloride

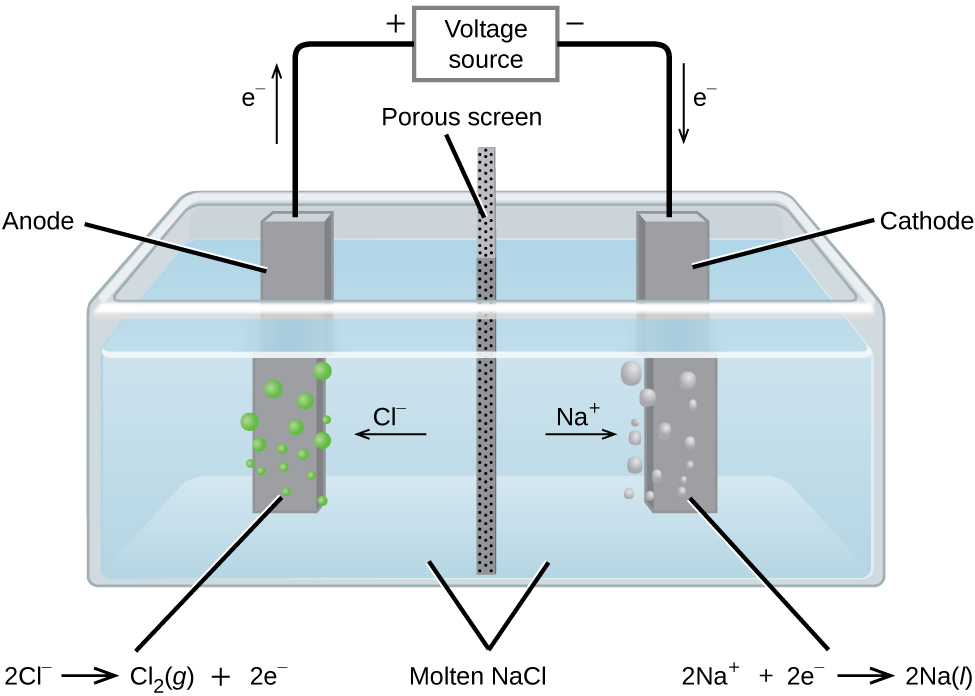
Metallic sodium, Na, and chlorine gas, [latex]\ce{Cl2}[/latex], are used in numerous applications, and their industrial production relies on the large-scale electrolysis of molten sodium chloride, NaCl(l). The industrial process typically uses a Downs cell similar to the simplified illustration shown in Figure 17.6.1. The reactions associated with this process are:

[latex]\text{anode:} \,\,\,\, \ce{2Cl-} (l) \longrightarrow \ce{Cl2} (g) + \ce{2e-}[/latex][latex]\text{cathode:} \,\,\,\, \ce{Na+} (l) + \ce{e-} \longrightarrow \ce{Na} (l)[/latex]
[latex]\text{cell:} \,\,\,\, \ce{2Na+} (l) + \ce{2Cl-} (l) \longrightarrow \ce{2Na} (l) + \ce{Cl2} (g)[/latex]

The cell potential for the above process is negative, indicating the reaction as written (decomposition of liquid [latex]\ce{NaCl}[/latex]) is not spontaneous. To force this reaction, a positive potential of magnitude greater than the negative cell potential must be applied to the cell.

This diagram shows a tank containing a light blue liquid, labeled “Molten N a C l.” A vertical dark grey divider with small, evenly distributed dark dots, labeled “Porous screen” is located at the center of the tank dividing it into two halves. Dark grey bars are positioned at the center of each of the halves of the tank. The bar on the left, which is labeled “Anode” has green bubbles originating from it. The bar on the right which is labeled “Cathode” has light grey bubbles originating from it. An arrow points left from the center of the tank toward the anode, which is labeled “C l superscript negative.” An arrow points right from the center of the tank toward the cathode, which is labeled “N a superscript plus.” A line extends from the tops of the anode and cathode to a rectangle centrally placed above the tank which is labeled “Voltage source.” An arrow extends upward above the anode to the left of the line which is labeled “e superscript negative.” A plus symbol is located to the left of the voltage source and a negative sign it located to its right. An arrow points downward along the line segment leading to the cathode. This arrow is labeled “e superscript negative.” The left side of below the diagram is the label “2 C l superscript negative right pointing arrow C l subscript 2 ( g ) plus 2 e superscript negative.” At the right, below the diagram is the label “2 N a superscript plus plus 2 e superscript negative right pointing arrow 2 N a ( l ).”
Figure 17.6.1. Cells of this sort (a cell for the electrolysis of molten sodium chloride) are used in the Downs process for production of sodium and chlorine, and they typically use iron cathodes and carbon anodes.

The Electrolysis of Water

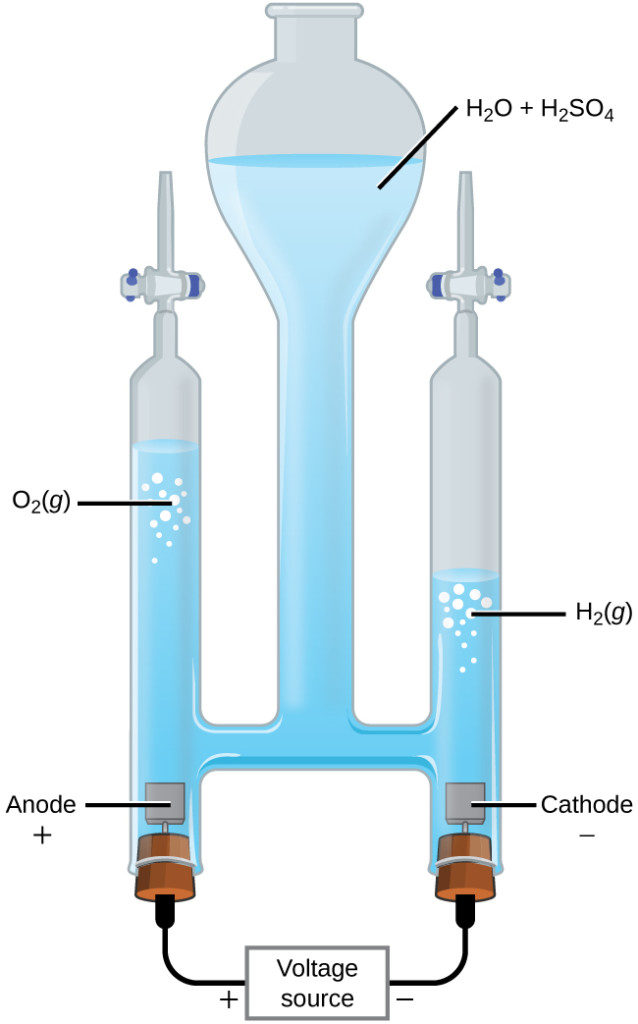
Water may be electrolytically decomposed in a cell similar to the one illustrated in Figure 17.6.2. To improve electrical conductivity without introducing a different redox species, the hydrogen ion concentration of the water is typically increased by addition of a strong acid. The redox processes associated with this cell are

[latex]\text{anode:} \,\,\,\, \ce{2H2O} (l) \longrightarrow \ce{O2} (g)+ \ce{4H+} (aq) + \ce{4e-} \,\,\,\,\, \text{E}^{\circ}_\text{anode} = +1.229\text{V}[/latex][latex]\text{cathode:} \,\,\,\, \ce{2H+} (aq) + \ce{2e-} \longrightarrow \text{H2}(g) \,\,\,\,\, \text{E}^{\circ}_\text{cathode} = 0\text{V}[/latex]
[latex]\text{cell:} \,\,\,\, \ce{2H2O} (l) \longrightarrow \ce{2H2} (g) + \ce{O2} (g) \,\,\,\,\, \text{E}^{\circ}_\text{cell} = -1.229\text{V}[/latex]

Again, the cell potential as written is negative, indicating a nonspontaneous cell reaction that must be driven by imposing a cell voltage greater than +1.229 V. Keep in mind that standard electrode potentials are used to inform thermodynamic predictions here, though the cell is not operating under standard state conditions. Therefore, at best, calculated cell potentials should be considered ballpark estimates.

This figure shows an apparatus used for electrolysis. A central chamber with an open top has a vertical column extending below that is nearly full of a clear, colorless liquid, which is labeled “H subscript 2 O plus H subscript 2 S O subscript 4.” A horizontal tube in the apparatus connects the central region to vertical columns to the left and right, each of which has a valve or stopcock at the top and a stoppered bottom. On the left, the stopper at the bottom has a small brown square connected just above it in the liquid. The square is labeled “Anode plus.” A black wire extends from the stopper at the left to a rectangle which is labeled “Voltage source” on to the stopper at the right. The left side of the rectangle is labeled with a plus symbol and the right side is labeled with a negative sign. The stopper on the right also has a brown square connected to it which is in the liquid in the apparatus. This square is labeled “Cathode negative.” The level of the solution on the left arm or tube of the apparatus is significantly higher than the level of the right arm. Bubbles are present near the surface of the liquid on each side of the apparatus, with the bubbles labeled as “O subscript 2 ( g )” on the left and “H subscript 2 ( g )” on the right.
Figure 17.6.2. The electrolysis of water produces stoichiometric amounts of oxygen gas at the anode and hydrogen at the anode.

The Electrolysis of Aqueous Sodium Chloride

When aqueous solutions of ionic compounds are electrolyzed, the anode and cathode half-reactions may involve the electrolysis of either water species ([latex]\ce{H2O}[/latex], [latex]\ce{H+}[/latex], [latex]\ce{OH-}[/latex]) or solute species (the cations and anions of the compound). As an example, the electrolysis of aqueous sodium chloride could involve either of these two anode reactions:

(i) [latex]\ce{2Cl-}(aq) \longrightarrow \ce{Cl2}(g) + \ce{2e-} \,\,\,\,\,\,\, \text{E}^\circ_{\text{anode}} = +1.35827 \text{V}[/latex]

(ii) [latex]\ce{2H2O}(l) \longrightarrow \ce{O2}(g) + \ce{4H+}(aq) + \ce{4e-}\,\,\,\,\,\,\,\text{E}^\circ_{\text{anode}}= +1.229 \text{V}[/latex]

The standard electrode (reduction) potentials of these two half-reactions indicate water may be oxidized at a less negative/more positive potential (–1.229 V) than chloride ion (–1.358 V). Thermodynamics thus predicts that water would be more readily oxidized, though in practice it is observed that both water and chloride ion are oxidized under typical conditions, producing a mixture of oxygen and chlorine gas.

Turning attention to the cathode, the possibilities for reduction are:

(iii) [latex]\ce{2H+}(aq) + \ce{2e-} \longrightarrow \ce{H2}(g) \,\,\,\,\,\,\, \text{E}^\circ_{\text{cathode}}= 0 \text{V}[/latex]

(iv) [latex]\ce{2H2O}(l) + \ce{2e-} \longrightarrow \ce{H2}(g) + \ce{2OH-}(aq) \,\,\,\,\,\,\, \text{E}^\circ_{\text{cathode}}= −0.8277 \text{V}[/latex]

(v) [latex]\ce{Na+}(aq) + \ce{e-} \longrightarrow \ce{Na}(s) \,\,\,\,\,\,\, \text{E}^\circ_{\text{cathode}}= −2.71 \text{V}[/latex]

Comparison of these standard half-reaction potentials suggests the reduction of hydrogen ion is thermodynamically favored. However, in a neutral aqueous sodium chloride solution, the concentration of hydrogen ion is far below the standard state value of 1 M (approximately 10-7 M), and so the observed cathode reaction is actually reduction of water. The net cell reaction in this case is then

[latex]\text{cell: } \ce{2H2O}(l) + \ce{Cl-}(aq) \longrightarrow \ce{H2}(g) + \ce{Cl2}(g) + \ce{2OH-}(aq) \,\,\,\,\,\,\, \text{E}^\circ_{\text{cell}} = −2.186 \text{V}[/latex]

This electrolysis reaction is part of the chlor-alkali process used by industry to produce chlorine and sodium hydroxide (lye).

Electroplating

An important use for electrolytic cells is in electroplating. Electroplating results in a thin coating of one metal on top of a conducting surface. Reasons for electroplating include making the object more corrosion resistant, strengthening the surface, producing a more attractive finish, or for purifying metal. The metals commonly used in electroplating include cadmium, chromium, copper, gold, nickel, silver, and tin. Common consumer products include silver-plated or gold-plated tableware, chrome-plated automobile parts, and jewelry. We can get an idea of how this works by investigating how silver-plated tableware is produced (Figure 17.6.3).

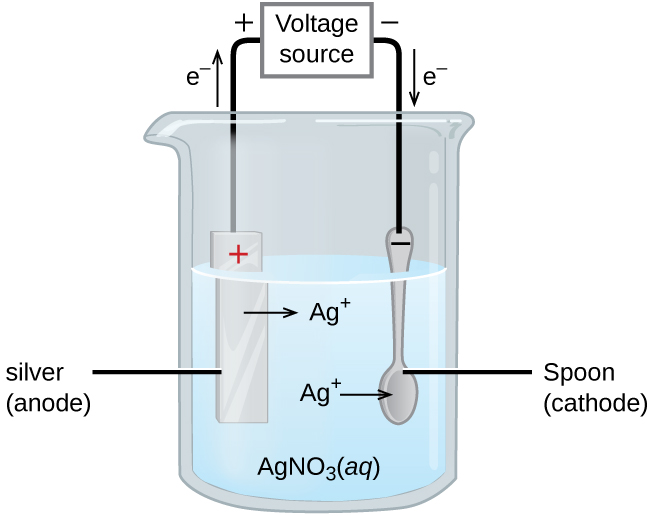
This figure contains a diagram of an electrochemical cell. One beakers is shown that is just over half full. The beaker contains a clear, colorless solution that is labeled “A g N O subscript 3 ( a q ).” A silver strip is mostly submerged in the liquid on the left. This strip is labeled “Silver (anode).” The top of the strip is labeled with a red plus symbol. An arrow points right from the surface of the metal strip into the solution to the label “A g superscript plus” to the right. A spoon is similarly suspended in the solution and is labeled “Spoon (cathode).” It is labeled with a black negative sign on the tip of the spoon’s handle above the surface of the liquid. An arrow extends from the label “A g superscript plus” to the spoon on the right. A wire extends from the top of the spoon and the strip to a rectangle labeled “Voltage source.” An arrow points upward from silver strip which is labeled “e superscript negative.” Similarly, an arrow points down at the right to the surface of the spoon which is also labeled “e superscript negative.” A plus sign is shown just outside the voltage source to the left and a negative is shown to its right.
Figure 17.6.3. The spoon, which is made of an inexpensive metal, is connected to the negative terminal of the voltage source and acts as the cathode. The anode is a silver electrode. Both electrodes are immersed in a silver nitrate solution. When a steady current is passed through the solution, the net result is that silver metal is removed from the anode and deposited on the cathode.

In Figure 17.6.3, the anode consists of a silver electrode, shown on the left. The cathode is located on the right and is the spoon, which is made from inexpensive metal. Both electrodes are immersed in a solution of silver nitrate. Applying a sufficient potential results in the oxidation of the silver anode

[latex]\text{anode: } \ce{Ag}(s) \longrightarrow \ce{Ag+}(aq) + \ce{e-}[/latex]

and reduction of silver ion at the (spoon) cathode:

[latex]\text{cathode: } \ce{Ag+}(aq) + \ce{e-} \longrightarrow \text{Ag}(s)[/latex]

The net result is the transfer of silver metal from the anode to the cathode. Several experimental factors must be carefully controlled to obtain high-quality silver coatings, including the exact composition of the electrolyte solution, the cell voltage applied, and the rate of the electrolysis reaction (electrical current).

Quantitative Aspects of Electrolysis

Electrical current is defined as the rate of flow for any charged species. Most relevant to this discussion is the flow of electrons. Current is measured in a composite unit called an ampere, defined as one coulomb per second (A = 1 C/s). The charge transferred, Q, by passage of a constant current, [latex]I[/latex], over a specified time interval, [latex]t[/latex], is then given by the simple mathematical product

[latex]Q =It[/latex]

When electrons are transferred during a redox process, the stoichiometry of the reaction may be used to derive the total amount of (electronic) charge involved. For example, the generic reduction process

[latex]\text{M}^{\text{n}+} (aq) + \text{ne}^- \longrightarrow \text{M} (s)[/latex]

involves the transfer of n mole of electrons. The charge transferred is, therefore,

[latex]Q =nF[/latex]

where F is Faraday’s constant, the charge in coulombs for one mole of electrons. If the reaction takes place in an electrochemical cell, the current flow is conveniently measured, and it may be used to assist in stoichiometric calculations related to the cell reaction.

Example 17.6.1: Converting Current to Moles of Electrons

In one process used for electroplating silver, a current of 10.23 A was passed through an electrolytic cell for exactly 1 hour. How many moles of electrons passed through the cell? What mass of silver was deposited at the cathode from the silver nitrate solution?

Show Solution

Faraday’s constant can be used to convert the charge (Q) into moles of electrons (n). The charge is the current (I) multiplied by the time

[latex]\displaystyle{n}=\frac{Q}{F}=\frac{\frac{10.23\text{ C}}{\text{s}}\times\text{1 hr}\times\frac{60\text{ min}}{\text{hr}}\times\frac{60\text{ s}}{\text{min}}}{\text{96,485 C/mol e}^-}=\frac{\text{36,830 C}}{\text{96,485 C/mol e}^-}=0.3817\text{ mol e}^-[/latex]

From the problem, the solution contains [latex]\ce{AgNO3}[/latex], so the reaction at the cathode involves 1 mole of electrons for each mole of silver

[latex]\text{cathode:} \ce{Ag}^+(aq) + \ce{e-} \longrightarrow \ce{Ag}(s)[/latex]

The atomic mass of silver is 107.9 g/mol, so

[latex]\text{mass } \ce{Ag} = 0.3817\text{ mol e}^-\times\dfrac{1\text{ mol } \ce{Ag}}{1\text{ mol e}^-}\times\dfrac{107.9\ce{ g } \ce{Ag}}{1\text{ mol Ag}}=41.19\text{ g } \ce{Ag}[/latex]

Check your answer: From the stoichiometry, 1 mole of electrons would produce 1 mole of silver. Less than one-half a mole of electrons was involved and less than one-half a mole of silver was produced.

Check Your Learning

Example 17.6.2: Time Required for Deposition

In one application, a 0.010-mm layer of chromium must be deposited on a part with a total surface area of 3.3 m2 from a solution of containing chromium(III) ions. How long would it take to deposit the layer of chromium if the current was 33.46 A? The density of chromium (metal) is 7.19 g/cm3.

Show Solution

This problem brings in a number of topics covered earlier. An outline of what needs to be done is:

  • If the total charge can be determined, the time required is just the charge divided by the current
  • The total charge can be obtained from the amount of [latex]\ce{Cr}[/latex] needed and the stoichiometry
  • The amount of [latex]\ce{Cr}[/latex] can be obtained using the density and the volume Cr required
  • The volume [latex]\ce{Cr}[/latex] required is the thickness times the area

Solving in steps, and taking care with the units, the volume of [latex]\ce{Cr}[/latex] required is

[latex]\text{volume}=\left(\text{0.010 mm}\times\frac{\text{1 cm}}{\text{10 mm}}\right)\times\left(\text{3.3 m}^{2}\times\left(\frac{\text{10,000 cm}^{2}}{\text{1 m}^2}\right)\right)=\text{33 cm}^3[/latex]

Cubic centimeters were used because they match the volume unit used for the density. The amount of [latex]\ce{Cr}[/latex] is then

mass = volume × density = [latex]33\cancel{\text{ cm}^3}\times\dfrac{7.19\text{ g}}{\cancel{\text{cm}^3}}=237\text{ g  } \ce{Cr}[/latex]
mol Cr [latex]= 237\text{ g } \ce{Cr}\times\dfrac{1\text{ mol } \ce{Cr}}{52.00\text{g } \ce{Cr}}=4.56\text{ mol  } \ce{Cr}[/latex]

Since the solution contains chromium(III) ions, 3 moles of electrons are required per mole of [latex]\ce{Cr}[/latex]. The total charge is then

[latex]Q=4.56\text{ mol } \ce{Cr}\times\dfrac{3\text{ mol e}^-}{1\text{ mol } \ce{Cr}}\times\dfrac{96485\ce{ C}}{\text{mol e}^-}=1.32\times{10^{6}}\ce{C}[/latex]

The time required is then

[latex]t=\frac{Q}{I}=\dfrac{1.32\times10^6\text{ C}}{33.46\text{ C/s}}=3.95\times10^4\text{ s}=11.0\text{hr}[/latex]

Check your answer: In a long problem like this, a single check is probably not enough. Each of the steps gives a reasonable number, so things are probably correct. Pay careful attention to unit conversions and the stoichiometry.

Check Your Learning

Key Concepts and Summary

Nonspontaneous redox processes may be forced to occur in electrochemical cells by the application of an appropriate potential using an external power source—a process known as electrolysis. Electrolysis is the basis for certain ore refining processes, the industrial production of many chemical commodities, and the electroplating of metal coatings on various products. Measurement of the current flow during electrolysis permits stoichiometric calculations.

Key Equations

  • [latex]Q = I \times{t} = n\times{F}[/latex]

Try It

  1. Identify the reaction at the anode, reaction at the cathode, the overall reaction, and the approximate potential required for the electrolysis of the following molten salts. Assume standard states and that the standard reduction potentials in Standard Electrode (Half-Cell) Potentials are the same as those at each of the melting points. Assume the efficiency is 100%.
    1. [latex]\ce{CaCl2}[/latex]
    2. [latex]\ce{LiH}[/latex]
    3. [latex]\ce{AlCl3}[/latex]
    4. [latex]\ce{CrBr3}[/latex]
  2. What mass of each product is produced in each of the electrolytic cells of the previous problem if a total charge of 3.33 × 105 [latex]\ce{C}[/latex] passes through each cell? Assume the voltage is sufficient to perform the reduction.
  3. How long would it take to reduce 1 mole of each of the following ions using the current indicated? Assume the voltage is sufficient to perform the reduction.
    1. [latex]\ce{Al^3+}[/latex], 1.234 A
    2. [latex]\ce{Ca^2+}[/latex], 22.2 A
    3. [latex]\ce{Cr^5+}[/latex], 37.45 A
    4. [latex]\ce{Au^3+}[/latex], 3.57 A
  4. A current of 2.345 A passes through the cell shown in Figure for 45 minutes. What is the volume of the hydrogen collected at room temperature if the pressure is exactly 1 atm? Assume the voltage is sufficient to perform the reduction. (Hint: Is hydrogen the only gas present above the water?)
  5. An irregularly shaped metal part made from a particular alloy was galvanized with zinc using a [latex]\ce{Zn(NO3)2}[/latex] solution. When a current of 2.599 A was used, it took exactly 1 hour to deposit a 0.01123-mm layer of zinc on the part. What was the total surface area of the part? The density of zinc is 7.140 g/cm3. Assume the efficiency is 100%.
Show Selected Solutions
  1. The masses are as follows:
    1. mass [latex]\ce{Ca}[/latex] = 69.1 g ; mass [latex]\ce{Cl2}[/latex] = 122 g
    2. mass [latex]\ce{Li}[/latex] = 23.9 g ; mass [latex]\ce{H2}[/latex] = 3.48 g
    3. mass [latex]\ce{Al}[/latex] = 31.0 g ; mass [latex]\ce{Cl2}[/latex] = 122 g
    4. mass [latex]\ce{Cr}[/latex] = 59.8 g ; mass [latex]\ce{Br2}[/latex] =276 g
  2. 0.79 L

Glossary

electrolysis: process using electrical energy to cause a nonspontaneous process to occur

electrolytic cell: electrochemical cell in which electrolysis is used; electrochemical cell with negative cell potentials

electroplating: depositing a thin layer of one metal on top of a conducting surface

overpotential: difference between the theoretical potential and actual potential in an electrolytic cell; the “extra” voltage required to make some nonspontaneous electrochemical reaction to occur

Licenses and Attributions (Click to expand)

CC licensed content, Shared previously

  • Chemistry 2e. Provided by: OpenStax. Located at: https://openstax.org/. License: CC BY: Attribution. License Terms: Access for free at
    https://openstax.org/books/chemistry-2e/pages/1-introduction

All rights reserved content

  • What Is Electrolysis | Reactions | Chemistry | FuseSchool. Authored by: FuseSchool – Global Education. Located at: https://youtu.be/7uIIq_Ofzgw. License: Other. License Terms: Standard YouTube License
definition

License

Icon for the Creative Commons Attribution-NonCommercial-ShareAlike 4.0 International License

Chemistry Fundamentals Copyright © by Dr. Julie Donnelly, Dr. Nicole Lapeyrouse, and Dr. Matthew Rex is licensed under a Creative Commons Attribution-NonCommercial-ShareAlike 4.0 International License, except where otherwise noted.

Share This Book