Chapter 9: Gases

9.4 Mixtures of Gases and Partial Pressures

Learning Outcomes

  • Relate the mole fraction, partial pressure, and quantity of gas in a mixture

The Pressure of a Mixture of Gases: Dalton’s Law

Unless they chemically react with each other, the individual gases in a mixture of gases do not affect each other’s pressure. Each individual gas in a mixture exerts the same pressure that it would exert if it present alone in the container (Figure 9.4.1). The pressure exerted by each individual gas in a mixture is called its partial pressure. This observation is summarized by Dalton’s law of partial pressures: The total pressure of a mixture of ideal gases is equal to the sum of the partial pressures of the component gases:

[latex]{P}_{Total}={P}_{A}+{P}_{B}+{P}_{C}+\ldots ={\Sigma}_{\text{i}}{P}_{\text{i}}[/latex]

In the equation PTotal is the total pressure of a mixture of gases, PA is the partial pressure of gas A; PB is the partial pressure of gas B; PC is the partial pressure of gas C; and so on.

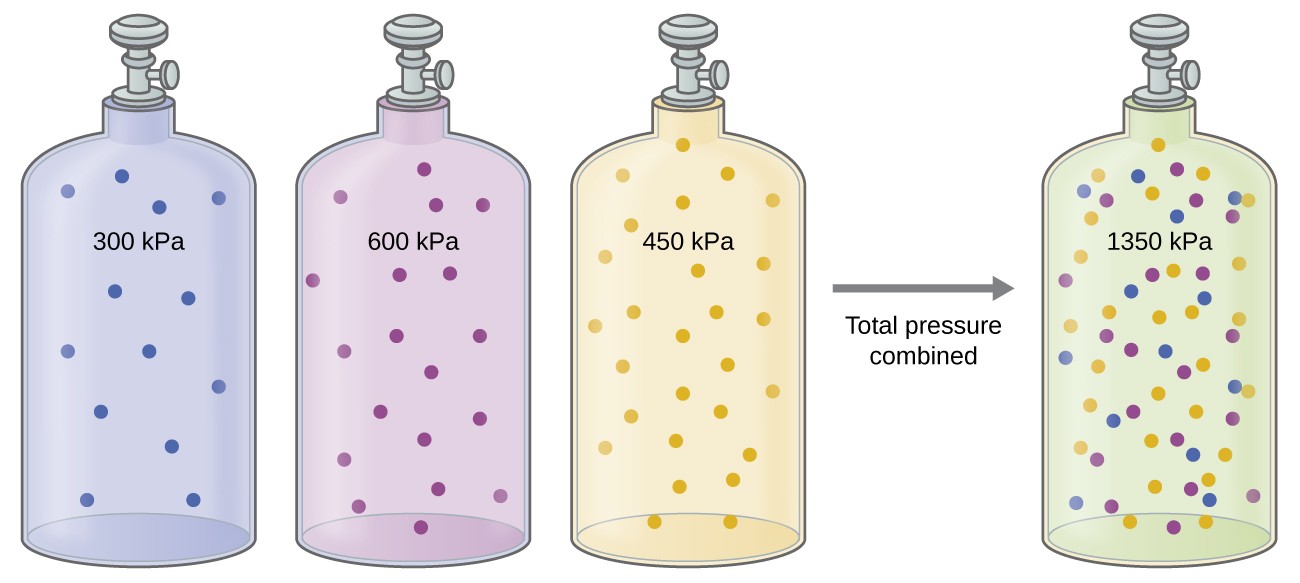
This figure includes images of four gas-filled cylinders or tanks. Each has a valve at the top. The interior of the first cylinder is shaded blue. This region contains 5 small blue circles that are evenly distributed. The label “300 k P a” is on the cylinder. The second cylinder is shaded lavender. This region contains 8 small purple circles that are evenly distributed. The label “600 k P a” is on the cylinder. To the right of these cylinders is a third cylinder. Its interior is shaded pale yellow. This region contains 12 small yellow circles that are evenly distributed. The label “450 k P a” is on this region of the cylinder. An arrow labeled “Total pressure combined” appears to the right of these three cylinders. This arrow points to a fourth cylinder. The interior of this cylinder is shaded a pale green. It contains evenly distributed small circles in the following quantities and colors; 5 blue, 8 purple, and 12 yellow. This cylinder is labeled “1350 k P a.”
Figure 9.4.1. If equal-volume cylinders containing gas A at a pressure of 300 kPa, gas B at a pressure of 600 kPa, and gas C at a pressure of 450 kPa are all combined in the same-size cylinder, the total pressure of the mixture is 1350 kPa.

The partial pressure of gas A is related to the total pressure of the gas mixture via its mole fraction, a unit of concentration defined as the number of moles of a component of a solution divided by the total number of moles of all components):

[latex]{P}_{A}={X}_{A}\times {P}_{Total}\qquad\text{ where }\qquad{X}_{A}=\dfrac{{n}_{A}}{{n}_{Total}}[/latex]

where PA, XA, and nA are the partial pressure, mole fraction, and number of moles of gas A, respectively, and nTotal is the number of moles of all components in the mixture.

Example 9.4.1: The Pressure of a Mixture of Gases

A 10.0-L vessel contains 2.50 × 10-3 mol of [latex]\ce{H2}[/latex], 1.00 × 10-3 mol of [latex]\ce{He}[/latex], and 3.00 × 10-4 mol of [latex]\ce{Ne}[/latex] at 35 °C.

  1. What are the partial pressures of each of the gases?
  2. What is the total pressure in atmospheres?
Show Solution

The gases behave independently, so the partial pressure of each gas can be determined from the ideal gas equation, using [latex]P=\dfrac{nRT}{V}:[/latex]

[latex]{P}_{{\text{H}}_{2}}=\dfrac{\left(2.50\times {10}^{-\text{3}}\cancel{\text{mol}}\right)\left(0.08206\cancel{\text{L}}\text{atm}\cancel{{\text{mol}}^{-\text{1}}{\text{K}}^{-\text{1}}}\right)\left(\text{308 K}\right)}{10.0\cancel{\text{L}}}=6.32\times {10}^{-\text{3}}\text{atm}[/latex]

[latex]{P}_{\text{He}}=\dfrac{\left(1.00\times {10}^{-\text{3}}\cancel{\text{mol}}\right)\left(\text{0.08206 L atm}\cancel{{\text{mol}}^{-\text{1}}{\text{K}}^{-\text{1}}}\right)\left(\text{308 K}\right)}{10.0\cancel{\text{L}}}=2.53\times {10}^{-\text{3}}\text{atm}[/latex]

[latex]{P}_{\text{Ne}}=\dfrac{\left(3.00\times {10}^{-\text{4}}\cancel{\text{mol}}\right)\left(0.08206\cancel{\text{L}}\text{atm}\cancel{{\text{mol}}^{-\text{1}}{\text{K}}^{-\text{1}}}\right)\left(\text{308 K}\right)}{10.0\cancel{\text{L}}}=7.58\times {10}^{-\text{4}}\text{atm}[/latex]

The total pressure is given by the sum of the partial pressures:

[latex]{P}_{\text{T}}={P}_{{\text{H}}_{2}}+{P}_{\text{He}}+{P}_{\text{Ne}}=\left(0.00632+0.00253+0.00076\right)\text{atm}=9.61\times {10}^{-\text{3}}\text{atm}[/latex]

Check Your Learning

Here is another example of this concept, but dealing with mole fraction calculations.

Example 9.4.2: The Pressure of a Mixture of Gases

A gas mixture used for anesthesia contains 2.83 mol oxygen, [latex]\ce{O2}[/latex], and 8.41 mol nitrous oxide, [latex]\ce{N2O}[/latex]. The total pressure of the mixture is 192 kPa.

  1. What are the mole fractions of [latex]\ce{O2}[/latex] and [latex]\ce{N2O}[/latex]?
  2. What are the partial pressures of [latex]\ce{O2}[/latex] and [latex]\ce{N2O}[/latex]?
Show Solution

The mole fraction is given by [latex]{X}_{A}=\dfrac{{n}_{A}}{{n}_{Total}}[/latex] and the partial pressure is PA = XA × PTotal.

For [latex]\ce{O2}[/latex],

[latex]{X}_{{O}_{2}}=\dfrac{{n}_{{O}_{2}}}{{n}_{Total}}=\dfrac{\text{2.83 mol}}{\left(2.83+8.41\right)\text{mol}}=0.252[/latex]

and

[latex]{P}_{{O}_{2}}={X}_{{O}_{2}}\times {P}_{Total}=0.252\times \text{192 kPa}=\text{48.4 kPa}[/latex]

For [latex]\ce{N2O}[/latex],

[latex]{X}_{{N}_{2}}=\dfrac{{n}_{{N}_{2}}}{{n}_{Total}}=\dfrac{\text{8.41 mol}}{\left(2.83+8.41\right)\text{mol}}=0.748[/latex]

and

[latex]{P}_{{N}_{2}}={X}_{{N}_{2}}\times {P}_{Total}=0.748 \times \text{192 kPa} = 143.6 \text{kPa}[/latex]

Check Your Learning

Collection of Gases over Water

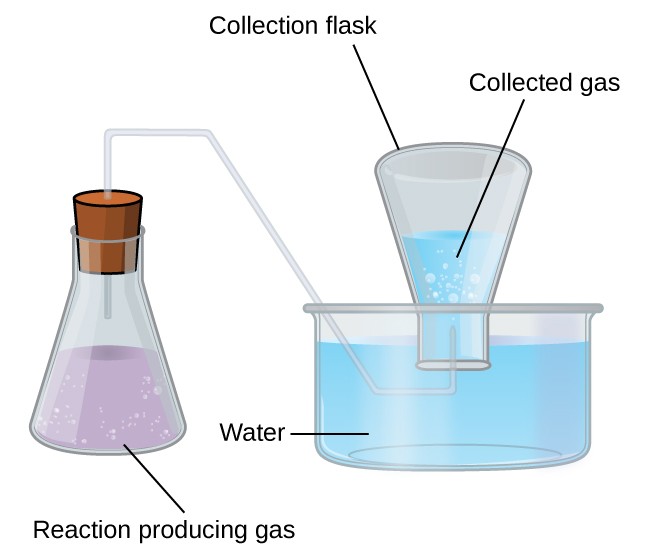
This figure shows a diagram of equipment used for collecting a gas over water. To the left is an Erlenmeyer flask. It is approximately two thirds full of a lavender colored liquid. Bubbles are evident in the liquid. The label “Reaction Producing Gas” appears below the flask. A line segment connects this label to the liquid in the flask. The flask has a stopper in it through which a single glass tube extends from the open region above the liquid in the flask up, through the stopper, to the right, then angles down into a pan that is nearly full of light blue water. This tube again extends right once it is well beneath the water’s surface. It then bends up into an inverted flask which is labeled “Collection Flask.” This collection flask is positioned with its mouth beneath the surface of the light blue water and appears approximately half full. Bubbles are evident in the water in the inverted flask. The open space above the water in the inverted flask is labeled “collected gas.”
Figure 9.4.2. When a reaction produces a gas that is collected above water, the trapped gas is a mixture of the gas produced by the reaction and water vapor. If the collection flask is appropriately positioned to equalize the water levels both within and outside the flask, the pressure of the trapped gas mixture will equal the atmospheric pressure outside the flask (see the earlier discussion of manometers).

A simple way to collect gases that do not react with water is to capture them in a bottle that has been filled with water and inverted into a dish filled with water. The pressure of the gas inside the bottle can be made equal to the air pressure outside by raising or lowering the bottle. When the water level is the same both inside and outside the bottle (Figure 9.4.2), the pressure of the gas is equal to the atmospheric pressure, which can be measured with a barometer.

However, there is another factor we must consider when we measure the pressure of the gas by this method. Water evaporates and there is always gaseous water (water vapor) above a sample of liquid water. As a gas is collected over water, it becomes saturated with water vapor and the total pressure of the mixture equals the partial pressure of the gas plus the partial pressure of the water vapor. The pressure of the pure gas is therefore equal to the total pressure minus the pressure of the water vapor—this is referred to as the “dry” gas pressure, that is, the pressure of the gas only, without water vapor. The vapor pressure of water, which is the pressure exerted by water vapor in equilibrium with liquid water in a closed container, depends on the temperature (Figure 9.4.3); more detailed information on the temperature dependence of water vapor can be found in Table 9.4.1, and vapor pressure will be discussed in more detail in the next chapter on liquids..

alt=
Figure 9.4.3. This graph shows the vapor pressure of water at sea level as a function of temperature.
Table 9.4.1: Vapor Pressure of Ice and Water in Various Temperatures at Sea Level
Temperature (°C) Pressure (torr) Temperature (°C) Pressure (torr) Temperature (°C) Pressure (torr)
–10 1.95 18 15.5 30 31.8
–5 3.0 19 16.5 35 42.2
–2 3.9 20 17.5 40 55.3
0 4.6 21 18.7 50 92.5
2 5.3 22 19.8 60 149.4
4 6.1 23 21.1 70 233.7
6 7.0 24 22.4 80 355.1
8 8.0 25 23.8 90 525.8
10 9.2 26 25.2 95 633.9
12 10.5 27 26.7 99 733.2
14 12.0 28 28.3 100.0 760.0
16 13.6 29 30.0 101.0 787.6

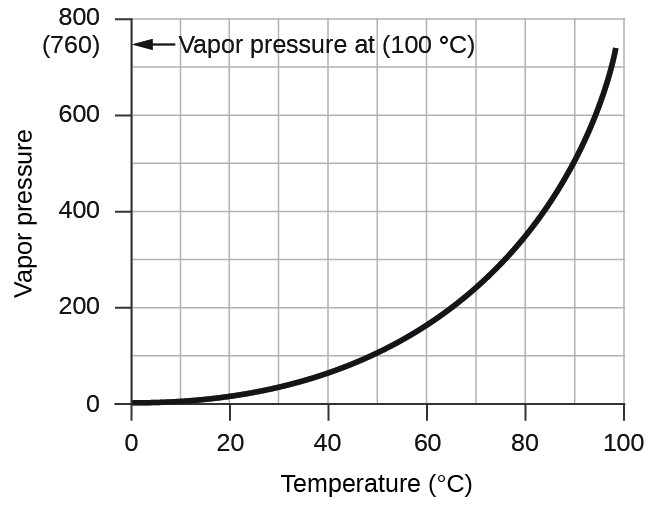
Example 9.4.3: Pressure of a Gas Collected Over Water

If 0.200 L of argon is collected over water at a temperature of 26 °C and a pressure of 750 torr in a system like that shown in Figure 3, what is the partial pressure of argon?

Show Solution

According to Dalton’s law, the total pressure in the bottle (750 torr) is the sum of the partial pressure of argon and the partial pressure of gaseous water:

[latex]{P}_{\text{T}}={P}_{\ce{Ar}}+{P}_{{\ce{H}}_{2}\ce{O}}[/latex]

Rearranging this equation to solve for the pressure of argon gives:

[latex]{P}_{\ce{Ar}}={P}_{\text{T}}-{P}_{{\ce{H}}_{2}\ce{O}}[/latex]

The pressure of water vapor above a sample of liquid water at 26 °C is 25.2 torr (Water Properties), so:

[latex]{P}_{\ce{Ar}}=750\text{ torr}-25.2\text{ torr}=725\text{ torr}[/latex]

Check Your Learning

Key Concepts and Summary

Dalton’s law of partial pressures may be used to relate measured gas pressures for gaseous mixtures to their compositions.

Key Equations

  • [latex]{P}_{Total}={P}_{A}+{P}_{B}+{P}_{C}+\ldots ={\Sigma}_{\text{i}}{P}_{\text{i}}[/latex]
  • [latex]{P}_{A}={X}_{A}\cdot {P}_{Total}[/latex]
  • [latex]{X}_{A}=\dfrac{{n}_{A}}{{n}_{Total}}[/latex]

Try It

  1. A sample of gas isolated from unrefined petroleum contains 90.0% [latex]\ce{CH4}[/latex], 8.9% [latex]\ce{C2H6}[/latex], and 1.1% [latex]\ce{C3H8}[/latex] at a total pressure of 307.2 kPa. What is the partial pressure of each component of this gas? (The percentages given indicate the percent of the total pressure that is due to each component.)
  2. A sample of carbon monoxide was collected over water at a total pressure of 756 torr and a temperature of 18 °C. What is the pressure of the carbon monoxide? (See Table 9.2 for the vapor pressure of water.)
Selected Answers
  1. Since these are percentages of the total pressure, the partial pressure can be calculated as follows:
    • [latex]\ce{CH^4}[/latex]: 90% of 307.2 kPa = 0.900 × 307.2 = 276 kPa
    • [latex]\ce{C^2 H^6}[/latex]: 8.9% of 307.2 kPa = 0.089 × 307.2 = 27 kPa
    • [latex]\ce{C^3 H^8}[/latex]: 1.1% of 307.2 kPa = 0.011 × 307.2 = 3.4 kPa
  2. The vapor pressure of water at 18 °C is 15.5 torr. Subtract the vapor pressure of water from the total pressure to find the pressure of the carbon monoxide:

  3. PT = Pgas + Pwater

  4. Rearrangement gives: PT – Pwater =Pgas

    756 torr – 15.5 torr = 740 torr

Glossary

Dalton’s law of partial pressures: total pressure of a mixture of ideal gases is equal to the sum of the partial pressures of the component gases.

mole fraction: concentration unit defined as the ratio of the molar amount of a mixture component to the total number of moles of all mixture components

partial pressure: pressure exerted by an individual gas in a mixture

vapor pressure of water: pressure exerted by water vapor in equilibrium with liquid water in a closed container at a specific temperature

definition

License

Icon for the Creative Commons Attribution-NonCommercial-ShareAlike 4.0 International License

Chemistry Fundamentals Copyright © by Dr. Julie Donnelly, Dr. Nicole Lapeyrouse, and Dr. Matthew Rex is licensed under a Creative Commons Attribution-NonCommercial-ShareAlike 4.0 International License, except where otherwise noted.

Share This Book