Chapter 16. Electromagnetic Waves
16.5 The Electromagnetic Spectrum
Learning Objectives
By the end of this section, you will be able to:
- Explain how electromagnetic waves are divided into different ranges, depending on wavelength and corresponding frequency
- Describe how electromagnetic waves in different categories are produced
- Describe some of the many practical everyday applications of electromagnetic waves
Electromagnetic waves have a vast range of practical everyday applications that includes such diverse uses as communication by cell phone and radio broadcasting, WiFi, cooking, vision, medical imaging, and treating cancer. In this module, we discuss how electromagnetic waves are classified into categories such as radio, infrared, ultraviolet, and so on. We also summarize some of the main applications for each range.
The different categories of electromagnetic waves differ in their wavelength range, or equivalently, in their corresponding frequency ranges. Their properties change smoothly from one frequency range to the next, with different applications in each range. A brief overview of the production and utilization of electromagnetic waves is found in Table 16.1.
| Type of wave | Production | Applications | Issues |
|---|---|---|---|
| Radio | Accelerating charges | Communications Remote controls MRI |
Requires control for band use |
| Microwaves | Accelerating charges and thermal agitation | Communications Ovens Radar Cell phone use |
|
| Infrared | Thermal agitation and electronic transitions | Thermal imaging Heating |
Absorbed by atmosphere Greenhouse effect |
| Visible light | Thermal agitation and electronic transitions | Photosynthesis Human vision |
|
| Ultraviolet | Thermal agitation and electronic transitions | Sterilization Vitamin D production |
Ozone depletion Cancer causing |
| X-rays | Inner electronic transitions and fast collisions | Security Medical diagnosis Cancer therapy |
Cancer causing |
| Gamma rays | Nuclear decay | Nuclear medicine Security Medical diagnosis Cancer therapy |
Cancer causing Radiation damage |
The relationship [latex]c=f\lambda[/latex] between frequency f and wavelength [latex]\lambda[/latex] applies to all waves and ensures that greater frequency means smaller wavelength. Figure 16.17 shows how the various types of electromagnetic waves are categorized according to their wavelengths and frequencies—that is, it shows the electromagnetic spectrum.
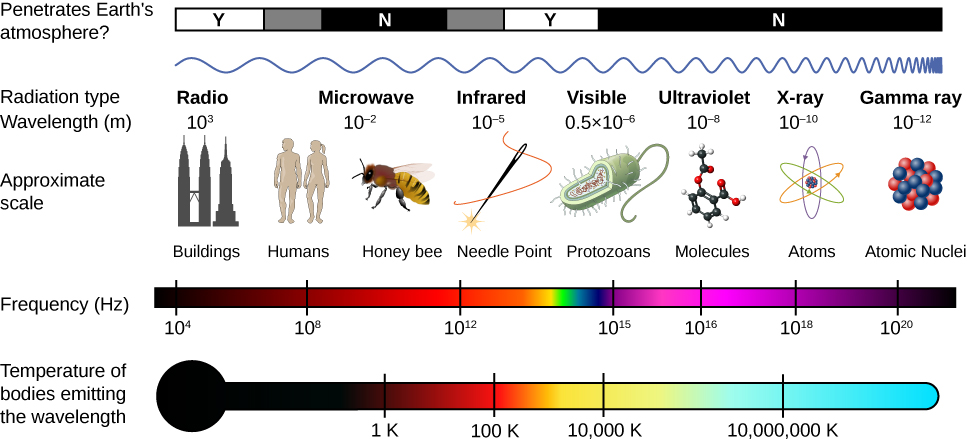
Radio Waves
The term radio waves refers to electromagnetic radiation with wavelengths greater than about 0.1 m. Radio waves are commonly used for audio communications (i.e., for radios), but the term is used for electromagnetic waves in this range regardless of their application. Radio waves typically result from an alternating current in the wires of a broadcast antenna. They cover a very broad wavelength range and are divided into many subranges, including microwaves, electromagnetic waves used for AM and FM radio, cellular telephones, and TV signals.
There is no lowest frequency of radio waves, but ELF waves, or “extremely low frequency” are among the lowest frequencies commonly encountered, from 3 Hz to 3 kHz. The accelerating charge in the ac currents of electrical power lines produce electromagnetic waves in this range. ELF waves are able to penetrate sea water, which strongly absorbs electromagnetic waves of higher frequency, and therefore are useful for submarine communications.
In order to use an electromagnetic wave to transmit information, the amplitude, frequency, or phase of the wave is modulated, or varied in a controlled way that encodes the intended information into the wave. In AM radio transmission, the amplitude of the wave is modulated to mimic the vibrations of the sound being conveyed. Fourier’s theorem implies that the modulated AM wave amounts to a superposition of waves covering some narrow frequency range. Each AM station is assigned a specific carrier frequency that, by international agreement, is allowed to vary by [latex]\text{±5 kHz}[/latex]. In FM radio transmission, the frequency of the wave is modulated to carry this information, as illustrated in Figure 16.18, and the frequency of each station is allowed to use 100 kHz on each side of its carrier frequency. The electromagnetic wave produces a current in a receiving antenna, and the radio or television processes the signal to produce the sound and any image. The higher the frequency of the radio wave used to carry the data, the greater the detailed variation of the wave that can be carried by modulating it over each time unit, and the more data that can be transmitted per unit of time. The assigned frequencies for AM broadcasting are 540 to 1600 kHz, and for FM are 88 MHz to108 MHz.
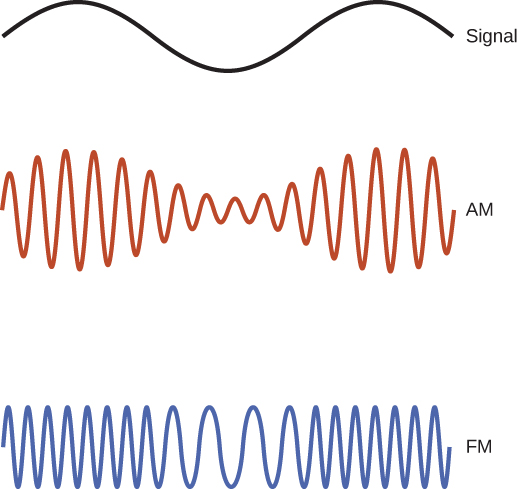
Cell phone conversations, and television voice and video images are commonly transmitted as digital data, by converting the signal into a sequence of binary ones and zeros. This allows clearer data transmission when the signal is weak, and allows using computer algorithms to compress the digital data to transmit more data in each frequency range. Computer data as well is transmitted as a sequence of binary ones and zeros, each one or zero constituting one bit of data.
Microwaves
Microwaves are the highest-frequency electromagnetic waves that can be produced by currents in macroscopic circuits and devices. Microwave frequencies range from about [latex]{10}^{9}\text{Hz}[/latex] to nearly [latex]{10}^{12}\text{Hz}[/latex]. Their high frequencies correspond to short wavelengths compared with other radio waves—hence the name “microwave.” Microwaves also occur naturally as the cosmic background radiation left over from the origin of the universe. Along with other ranges of electromagnetic waves, they are part of the radiation that any object above absolute zero emits and absorbs because of thermal agitation, that is, from the thermal motion of its atoms and molecules.
Most satellite-transmitted information is carried on microwaves. Radar is a common application of microwaves. By detecting and timing microwave echoes, radar systems can determine the distance to objects as diverse as clouds, aircraft, or even the surface of Venus.
Microwaves of 2.45 GHz are commonly used in microwave ovens. The electrons in a water molecule tend to remain closer to the oxygen nucleus than the hydrogen nuclei (Figure 16.19). This creates two separated centers of equal and opposite charges, giving the molecule a dipole moment (see Electric Field). The oscillating electric field of the microwaves inside the oven exerts a torque that tends to align each molecule first in one direction and then in the other, with the motion of each molecule coupled to others around it. This pumps energy into the continual thermal motion of the water to heat the food. The plate under the food contains no water, and remains relatively unheated.
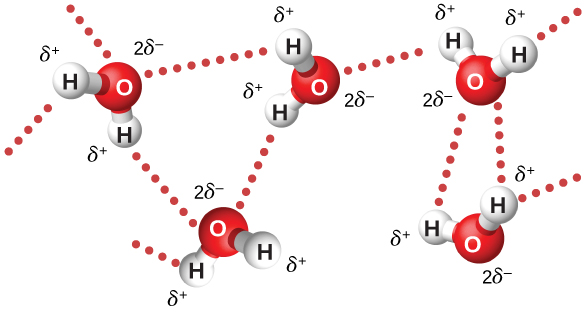
The microwaves in a microwave oven reflect off the walls of the oven, so that the superposition of waves produces standing waves, similar to the standing waves of a vibrating guitar or violin string (see Normal Modes of a Standing Sound Wave). A rotating fan acts as a stirrer by reflecting the microwaves in different directions, and food turntables, help spread out the hot spots.
Example
Why Microwave Ovens Heat Unevenly
How far apart are the hotspots in a 2.45-GHz microwave oven?
Strategy
Consider the waves along one direction in the oven, being reflected at the opposite wall from where they are generated.
Solution
Show Answer
The antinodes, where maximum intensity occurs, are half the wavelength apart, with separation
Significance
The distance between the hot spots in a microwave oven are determined by the wavelength of the microwaves.
A cell phone has a radio receiver and a weak radio transmitter, both of which can quickly tune to hundreds of specifically assigned microwave frequencies. The low intensity of the transmitted signal gives it an intentionally limited range. A ground-based system links the phone to only to the broadcast tower assigned to the specific small area, or cell, and smoothly transitions its connection to the next cell when the signal reception there is the stronger one. This enables a cell phone to be used while changing location.
Microwaves also provide the WiFi that enables owners of cell phones, laptop computers, and similar devices to connect wirelessly to the Internet at home and at coffee shops and airports. A wireless WiFi router is a device that exchanges data over the Internet through the cable or another connection, and uses microwaves to exchange the data wirelessly with devices such as cell phones and computers. The term WiFi itself refers to the standards followed in modulating and analyzing the microwaves so that wireless routers and devices from different manufacturers work compatibly with one another. The computer data in each direction consist of sequences of binary zeros and ones, each corresponding to a binary bit. The microwaves are in the range of 2.4 GHz to 5.0 GHz range.
Other wireless technologies also use microwaves to provide everyday communications between devices. Bluetooth developed alongside WiFi as a standard for radio communication in the 2.4-GHz range between nearby devices, for example, to link to headphones and audio earpieces to devices such as radios, or a driver’s cell phone to a hands-free device to allow answering phone calls without fumbling directly with the cell phone.
Microwaves find use also in radio tagging, using RFID (radio frequency identification) technology. Examples are RFID tags attached to store merchandize, transponder for toll booths use attached to the windshield of a car, or even a chip embedded into a pet’s skin. The device responds to a microwave signal by emitting a signal of its own with encoded information, allowing stores to quickly ring up items at their cash registers, drivers to charge tolls to their account without stopping, and lost pets to be reunited with their owners. NFC (near field communication) works similarly, except it is much shorter range. Its mechanism of interaction is the induced magnetic field at microwave frequencies between two coils. Cell phones that have NFC capability and the right software can supply information for purchases using the cell phone instead of a physical credit card. The very short range of the data transfer is a desired security feature in this case.
Infrared Radiation
The boundary between the microwave and infrared regions of the electromagnetic spectrum is not well defined (see Figure 16.17). Infrared radiation is generally produced by thermal motion, and the vibration and rotation of atoms and molecules. Electronic transitions in atoms and molecules can also produce infrared radiation. About half of the solar energy arriving at Earth is in the infrared region, with most of the rest in the visible part of the spectrum. About 23% of the solar energy is absorbed in the atmosphere, about 48% is absorbed at Earth’s surface, and about 29% is reflected back into space.1
The range of infrared frequencies extends up to the lower limit of visible light, just below red. In fact, infrared means “below red.” Water molecules rotate and vibrate particularly well at infrared frequencies. Reconnaissance satellites can detect buildings, vehicles, and even individual humans by their infrared emissions, whose power radiation is proportional to the fourth power of the absolute temperature. More mundanely, we use infrared lamps, including those called quartz heaters, to preferentially warm us because we absorb infrared better than our surroundings.
The familiar handheld “remotes” for changing channels and settings on television sets often transmit their signal by modulating an infrared beam. If you try to use a TV remote without the infrared emitter being in direct line of sight with the infrared detector, you may find the television not responding. Some remotes use Bluetooth instead and reduce this annoyance.
Visible Light
Visible light is the narrow segment of the electromagnetic spectrum between about 400 nm and about 750 nm to which the normal human eye responds. Visible light is produced by vibrations and rotations of atoms and molecules, as well as by electronic transitions within atoms and molecules. The receivers or detectors of light largely utilize electronic transitions.
Red light has the lowest frequencies and longest wavelengths, whereas violet has the highest frequencies and shortest wavelengths (Figure 16.20). Blackbody radiation from the Sun peaks in the visible part of the spectrum but is more intense in the red than in the violet, making the sun yellowish in appearance.
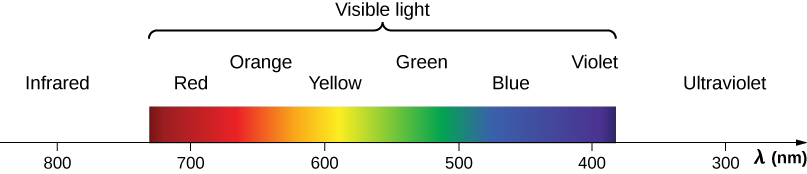
Living things—plants and animals—have evolved to utilize and respond to parts of the electromagnetic spectrum in which they are embedded. We enjoy the beauty of nature through visible light. Plants are more selective. Photosynthesis uses parts of the visible spectrum to make sugars.
Ultraviolet Radiation
Ultraviolet means “above violet.” The electromagnetic frequencies of ultraviolet radiation (UV) extend upward from violet, the highest-frequency visible light. The highest-frequency ultraviolet overlaps with the lowest-frequency X-rays. The wavelengths of ultraviolet extend from 400 nm down to about 10 nm at its highest frequencies. Ultraviolet is produced by atomic and molecular motions and electronic transitions.
UV radiation from the Sun is broadly subdivided into three wavelength ranges: UV-A (320–400 nm) is the lowest frequency, then UV-B (290–320 nm) and UV-C (220–290 nm). Most UV-B and all UV-C are absorbed by ozone ([latex]{\text{O}}_{3}[/latex]) molecules in the upper atmosphere. Consequently, 99% of the solar UV radiation reaching Earth’s surface is UV-A.
Sunburn is caused by large exposures to UV-B and UV-C, and repeated exposure can increase the likelihood of skin cancer. The tanning response is a defense mechanism in which the body produces pigments in inert skin layers to reduce exposure of the living cells below.
As examined in a later chapter, the shorter the wavelength of light, the greater the energy change of an atom or molecule that absorbs the light in an electronic transition. This makes short-wavelength ultraviolet light damaging to living cells. It also explains why ultraviolet radiation is better able than visible light to cause some materials to glow, or fluoresce.
Besides the adverse effects of ultraviolet radiation, there are also benefits of exposure in nature and uses in technology. Vitamin D production in the skin results from exposure to UV-B radiation, generally from sunlight. Several studies suggest vitamin D deficiency is associated with the development of a range of cancers (prostate, breast, colon), as well as osteoporosis. Low-intensity ultraviolet has applications such as providing the energy to cause certain dyes to fluoresce and emit visible light, for example, in printed money to display hidden watermarks as counterfeit protection.
X-Rays
X-rays have wavelengths from about [latex]{10}^{\text{−}8}{\text{m to}\phantom{\rule{0.2em}{0ex}}10}^{\text{−}12}\text{m}[/latex]. They have shorter wavelengths, and higher frequencies, than ultraviolet, so that the energy they transfer at an atomic level is greater. As a result, X-rays have adverse effects on living cells similar to those of ultraviolet radiation, but they are more penetrating. Cancer and genetic defects can be induced by X-rays. Because of their effect on rapidly dividing cells, X-rays can also be used to treat and even cure cancer.
The widest use of X-rays is for imaging objects that are opaque to visible light, such as the human body or aircraft parts. In humans, the risk of cell damage is weighed carefully against the benefit of the diagnostic information obtained.
Gamma Rays
Soon after nuclear radioactivity was first detected in 1896, it was found that at least three distinct types of radiation were being emitted, and these were designated as alpha, beta, and gamma rays. The most penetrating nuclear radiation, the gamma ray ([latex]\gamma[/latex] ray), was later found to be an extremely high-frequency electromagnetic wave.
The lower end of the [latex]\gamma \text{-}[/latex] ray frequency range overlaps the upper end of the X-ray range. Gamma rays have characteristics identical to X-rays of the same frequency—they differ only in source. The name “gamma rays” is generally used for electromagnetic radiation emitted by a nucleus, while X-rays are generally produced by bombarding a target with energetic electrons in an X-ray tube. At higher frequencies, [latex]\gamma[/latex] rays are more penetrating and more damaging to living tissue. They have many of the same uses as X-rays, including cancer therapy. Gamma radiation from radioactive materials is used in nuclear medicine.
Use this simulation to explore how light interacts with molecules in our atmosphere.
Explore how light interacts with molecules in our atmosphere.
Identify that absorption of light depends on the molecule and the type of light.
Relate the energy of the light to the resulting motion.
Identify that energy increases from microwave to ultraviolet.
Predict the motion of a molecule based on the type of light it absorbs.
Check Your Understanding
How do the electromagnetic waves for the different kinds of electromagnetic radiation differ?
Show Solution
They fall into different ranges of wavelength, and therefore also different corresponding ranges of frequency.
Summary
- The relationship among the speed of propagation, wavelength, and frequency for any wave is given by [latex]v=f\lambda ,[/latex] so that for electromagnetic waves, [latex]c=f\lambda ,[/latex] where f is the frequency, [latex]\lambda[/latex] is the wavelength, and c is the speed of light.
- The electromagnetic spectrum is separated into many categories and subcategories, based on the frequency and wavelength, source, and uses of the electromagnetic waves.
Key Equations
| Displacement current | [latex]{I}_{\text{d}}={\epsilon }_{0}\frac{d{\text{Φ}}_{\text{E}}}{dt}[/latex] |
| Gauss’s law | [latex]\oint \stackrel{\to }{\textbf{E}}·d\stackrel{\to }{\textbf{A}}=\frac{{Q}_{\text{in}}}{{\epsilon }_{0}}[/latex] |
| Gauss’s law for magnetism | [latex]\oint \stackrel{\to }{\textbf{B}}·d\stackrel{\to }{\textbf{A}}=0[/latex] |
| Faraday’s law | [latex]\oint \stackrel{\to }{\textbf{E}}·d\stackrel{\to }{\textbf{s}}=-\frac{d{\text{Φ}}_{\text{m}}}{dt}[/latex] |
| Ampère-Maxwell law | [latex]\oint \stackrel{\to }{\textbf{B}}·d\stackrel{\to }{\textbf{s}}={\mu }_{0}I+{\epsilon }_{0}{\mu }_{0}\frac{d{\text{Φ}}_{\text{E}}}{dt}[/latex] |
| Wave equation for plane EM wave | [latex]\frac{{\partial }^{2}{E}_{y}}{\partial {x}^{2}}={\epsilon }_{0}{\mu }_{0}\frac{{\partial }^{2}{E}_{y}}{\partial {t}^{2}}[/latex] |
| Speed of EM waves | [latex]c=\frac{1}{\sqrt{{\epsilon }_{0}{\mu }_{0}}}[/latex] |
| Ratio of E field to B field in electromagnetic wave | [latex]c=\frac{E}{B}[/latex] |
| Energy flux (Poynting) vector | [latex]\stackrel{\to }{\textbf{S}}=\frac{1}{{\mu }_{0}}\stackrel{\to }{\textbf{E}}\phantom{\rule{0.2em}{0ex}}×\phantom{\rule{0.2em}{0ex}}\stackrel{\to }{\textbf{B}}[/latex] |
| Average intensity of an electromagnetic wave | [latex]I={S}_{\text{avg}}=\frac{c{\epsilon }_{0}{E}_{0}^{2}}{2}=\frac{c{B}_{0}^{2}}{2{\mu }_{0}}=\frac{{E}_{0}{B}_{0}}{2{\mu }_{0}}[/latex] |
| Radiation pressure | [latex]p=\{\begin{array}{cccc}I\text{/}c\hfill & & & \text{Perfect absorber}\hfill \\ 2I\text{/}c\hfill & & & \text{Perfect reflector}\hfill \end{array}[/latex] |
Conceptual Questions
Compare the speed, wavelength, and frequency of radio waves and X-rays traveling in a vacuum.
Accelerating electric charge emits electromagnetic radiation. How does this apply in each case: (a) radio waves, (b) infrared radiation.
Show Solution
a. Radio waves are generally produced by alternating current in a wire or an oscillating electric field between two plates; b. Infrared radiation is commonly produced by heated bodies whose atoms and the charges in them vibrate at about the right frequency.
Compare and contrast the meaning of the prefix “micro” in the names of SI units in the term microwaves.
Part of the light passing through the air is scattered in all directions by the molecules comprising the atmosphere. The wavelengths of visible light are larger than molecular sizes, and the scattering is strongest for wavelengths of light closest to sizes of molecules.
(a) Which of the main colors of light is scattered the most? (b) Explain why this would give the sky its familiar background color at midday.
Show Solution
a. blue; b. Light of longer wavelengths than blue passes through the air with less scattering, whereas more of the blue light is scattered in different directions in the sky to give it is blue color.
When a bowl of soup is removed from a microwave oven, the soup is found to be steaming hot, whereas the bowl is only warm to the touch. Discuss the temperature changes that have occurred in terms of energy transfer.
Certain orientations of a broadcast television antenna give better reception than others for a particular station. Explain.
Show Solution
A typical antenna has a stronger response when the wires forming it are orientated parallel to the electric field of the radio wave.
What property of light corresponds to loudness in sound?
Is the visible region a major portion of the electromagnetic spectrum?
Show Solution
No, it is very narrow and just a small portion of the overall electromagnetic spectrum.
Can the human body detect electromagnetic radiation that is outside the visible region of the spectrum?
Radio waves normally have their E and B fields in specific directions, whereas visible light usually has its E and B fields in random and rapidly changing directions that are perpendicular to each other and to the propagation direction. Can you explain why?
Show Solution
Visible light is typically produced by changes of energies of electrons in randomly oriented atoms and molecules. Radio waves are typically emitted by an ac current flowing along a wire, that has fixed orientation and produces electric fields pointed in particular directions.
Give an example of resonance in the reception of electromagnetic waves.
Illustrate that the size of details of an object that can be detected with electromagnetic waves is related to their wavelength, by comparing details observable with two different types (for example, radar and visible light).
Show Solution
Radar can observe objects the size of an airplane and uses radio waves of about 0.5 cm in wavelength. Visible light can be used to view single biological cells and has wavelengths of about [latex]{10}^{-7}\phantom{\rule{0.2em}{0ex}}\text{m}[/latex].
In which part of the electromagnetic spectrum are each of these waves:
(a) f = 10.0 kHz, (b) [latex]f=\lambda =750\phantom{\rule{0.2em}{0ex}}\text{nm}[/latex],
(c) [latex]f=1.25\phantom{\rule{0.2em}{0ex}}×\phantom{\rule{0.2em}{0ex}}{10}^{8}\phantom{\rule{0.2em}{0ex}}\text{Hz}[/latex], (d) 0.30 nm
In what range of electromagnetic radiation are the electromagnetic waves emitted by power lines in a country that uses 50-Hz ac current?
Show Solution
ELF radio waves
If a microwave oven could be modified to merely tune the waves generated to be in the infrared range instead of using microwaves, how would this affect the uneven heating of the oven?
A leaky microwave oven in a home can sometimes cause interference with the homeowner’s WiFi system. Why?
Show Solution
The frequency of 2.45 GHz of a microwave oven is close to the specific frequencies in the 2.4 GHz band used for WiFi.
When a television news anchor in a studio speaks to a reporter in a distant country, there is sometimes a noticeable lag between when the anchor speaks in the studio and when the remote reporter hears it and replies. Explain what causes this delay.
Problems
How many helium atoms, each with a radius of about 31 pm, must be placed end to end to have a length equal to one wavelength of 470 nm blue light?
If you wish to detect details of the size of atoms (about 0.2 nm) with electromagnetic radiation, it must have a wavelength of about this size. (a) What is its frequency? (b) What type of electromagnetic radiation might this be?
Show Solution
a. [latex]1.5\phantom{\rule{0.2em}{0ex}}×\phantom{\rule{0.2em}{0ex}}{10}^{18}\phantom{\rule{0.2em}{0ex}}\text{Hz}[/latex]; b. X-rays
Find the frequency range of visible light, given that it encompasses wavelengths from 380 to 760 nm.
(a) Calculate the wavelength range for AM radio given its frequency range is 540 to 1600 kHz. (b) Do the same for the FM frequency range of 88.0 to 108 MHz.
Show Solution
a. The wavelength range is 187 m to 556 m. b. The wavelength range is 2.78 m to 3.41 m.
Radio station WWVB, operated by the National Institute of Standards and Technology (NIST) from Fort Collins, Colorado, at a low frequency of 60 kHz, broadcasts a time synchronization signal whose range covers the entire continental US. The timing of the synchronization signal is controlled by a set of atomic clocks to an accuracy of [latex]1\phantom{\rule{0.2em}{0ex}}×\phantom{\rule{0.2em}{0ex}}{10}^{-12}\phantom{\rule{0.2em}{0ex}}\text{s},[/latex] and repeats every 1 minute. The signal is used for devices, such as radio-controlled watches, that automatically synchronize with it at preset local times. WWVB’s long wavelength signal tends to propagate close to the ground.
(a) Calculate the wavelength of the radio waves from WWVB.
(b) Estimate the error that the travel time of the signal causes in synchronizing a radio controlled watch in Norfolk, Virginia, which is 1570 mi (2527 km) from Fort Collins, Colorado.
An outdoor WiFi unit for a picnic area has a 100-mW output and a range of about 30 m. What output power would reduce its range to 12 m for use with the same devices as before? Assume there are no obstacles in the way and that microwaves into the ground are simply absorbed.
Show Solution
[latex]P\text{′}={\left(\frac{12\phantom{\rule{0.2em}{0ex}}\text{m}}{30\phantom{\rule{0.2em}{0ex}}\text{m}}\right)}^{2}\left(100\phantom{\rule{0.2em}{0ex}}\text{mW}\right)=16\phantom{\rule{0.2em}{0ex}}\text{mW}[/latex]
The prefix “mega” (M) and “kilo” (k), when referring to amounts of computer data, refer to factors of 1024 or [latex]{2}^{10}[/latex] rather than 1000 for the prefix kilo, and [latex]{1024}^{2}={2}^{20}[/latex] rather than 1,000,000 for the prefix Mega (M). If a wireless (WiFi) router transfers 150 Mbps of data, how many bits per second is that in decimal arithmetic?
A computer user finds that his wireless router transmits data at a rate of 75 Mbps (megabits per second). Compare the average time to transmit one bit of data with the time difference between the wifi signal reaching an observer’s cell phone directly and by bouncing back to the observer from a wall 8.00 m past the observer.
Show Solution
time for [latex]1\phantom{\rule{0.2em}{0ex}}\text{bit}=1.27\phantom{\rule{0.2em}{0ex}}×\phantom{\rule{0.2em}{0ex}}{10}^{-8}\phantom{\rule{0.2em}{0ex}}\text{s},[/latex] difference in travel time is [latex]5.34\phantom{\rule{0.2em}{0ex}}×\phantom{\rule{0.2em}{0ex}}{10}^{-8}\phantom{\rule{0.2em}{0ex}}\text{s}[/latex]
(a) The ideal size (most efficient) for a broadcast antenna with one end on the ground is one-fourth the wavelength ([latex]\lambda \text{/}4[/latex]) of the electromagnetic radiation being sent out. If a new radio station has such an antenna that is 50.0 m high, what frequency does it broadcast most efficiently? Is this in the AM or FM band? (b) Discuss the analogy of the fundamental resonant mode of an air column closed at one end to the resonance of currents on an antenna that is one-fourth their wavelength.
What are the wavelengths of (a) X-rays of frequency [latex]2.0\phantom{\rule{0.2em}{0ex}}×\phantom{\rule{0.2em}{0ex}}{10}^{17}\phantom{\rule{0.2em}{0ex}}\text{Hz?}[/latex] (b) Yellow light of frequency [latex]5.1\phantom{\rule{0.2em}{0ex}}×\phantom{\rule{0.2em}{0ex}}{10}^{14}\phantom{\rule{0.2em}{0ex}}\text{Hz?}[/latex] (c) Gamma rays of frequency [latex]1.0\phantom{\rule{0.2em}{0ex}}×\phantom{\rule{0.2em}{0ex}}{10}^{23}\phantom{\rule{0.2em}{0ex}}\text{Hz?}[/latex]
Show Solution
a. [latex]1.5\phantom{\rule{0.2em}{0ex}}×\phantom{\rule{0.2em}{0ex}}{10}^{-9}\phantom{\rule{0.2em}{0ex}}\text{m;}[/latex] b. [latex]5.9\phantom{\rule{0.2em}{0ex}}×\phantom{\rule{0.2em}{0ex}}{10}^{-7}\phantom{\rule{0.2em}{0ex}}\text{m;}[/latex] c. [latex]3.0\phantom{\rule{0.2em}{0ex}}×\phantom{\rule{0.2em}{0ex}}{10}^{-15}\phantom{\rule{0.2em}{0ex}}\text{m}[/latex]
For red light of [latex]\lambda =660\phantom{\rule{0.2em}{0ex}}\text{nm}[/latex], what are f, [latex]\omega[/latex], and k?
A radio transmitter broadcasts plane electromagnetic waves whose maximum electric field at a particular location is [latex]1.55\phantom{\rule{0.2em}{0ex}}×\phantom{\rule{0.2em}{0ex}}{10}^{-3}\phantom{\rule{0.2em}{0ex}}\text{V/m}.[/latex] What is the maximum magnitude of the oscillating magnetic field at that location? How does it compare with Earth’s magnetic field?
Show Solution
[latex]5.17\phantom{\rule{0.2em}{0ex}}×\phantom{\rule{0.2em}{0ex}}{10}^{-12}\phantom{\rule{0.2em}{0ex}}\text{T},[/latex] the non-oscillating geomagnetic field of 25–65 [latex]\text{μT}[/latex] is much larger
(a) Two microwave frequencies authorized for use in microwave ovens are: 915 and 2450 MHz. Calculate the wavelength of each. (b) Which frequency would produce smaller hot spots in foods due to interference effects?
During normal beating, the heart creates a maximum 4.00-mV potential across 0.300 m of a person’s chest, creating a 1.00-Hz electromagnetic wave. (a) What is the maximum electric field strength created? (b) What is the corresponding maximum magnetic field strength in the electromagnetic wave? (c) What is the wavelength of the electromagnetic wave?
Show Solution
a. [latex]1.33\phantom{\rule{0.2em}{0ex}}×\phantom{\rule{0.2em}{0ex}}{10}^{\text{−}2}\phantom{\rule{0.2em}{0ex}}\text{V/m}[/latex]; b. [latex]4.44\phantom{\rule{0.2em}{0ex}}×\phantom{\rule{0.2em}{0ex}}{10}^{\text{−}11}\phantom{\rule{0.2em}{0ex}}\text{T}[/latex]; c. [latex]3.00\phantom{\rule{0.2em}{0ex}}×\phantom{\rule{0.2em}{0ex}}{10}^{8}\phantom{\rule{0.2em}{0ex}}\text{m}[/latex]
Distances in space are often quoted in units of light-years, the distance light travels in 1 year. (a) How many meters is a light-year? (b) How many meters is it to Andromeda, the nearest large galaxy, given that it is [latex]2.54\phantom{\rule{0.2em}{0ex}}×\phantom{\rule{0.2em}{0ex}}{10}^{6}[/latex] ly away? (c) The most distant galaxy yet discovered is [latex]13.4\phantom{\rule{0.2em}{0ex}}×\phantom{\rule{0.2em}{0ex}}{10}^{9}[/latex] ly away. How far is this in meters?
A certain 60.0-Hz ac power line radiates an electromagnetic wave having a maximum electric field strength of 13.0 kV/m. (a) What is the wavelength of this very-low-frequency electromagnetic wave? (b) What type of electromagnetic radiation is this wave (b) What is its maximum magnetic field strength?
Show Solution
a. [latex]5.00\phantom{\rule{0.2em}{0ex}}×\phantom{\rule{0.2em}{0ex}}{10}^{6}\text{m}[/latex]; b. radio wave; c. [latex]4.33\phantom{\rule{0.2em}{0ex}}×\phantom{\rule{0.2em}{0ex}}{10}^{-5}\text{T}[/latex]
(a) What is the frequency of the 193-nm ultraviolet radiation used in laser eye surgery? (b) Assuming the accuracy with which this electromagnetic radiation can ablate (reshape) the cornea is directly proportional to wavelength, how much more accurate can this UV radiation be than the shortest visible wavelength of light?
Additional Problems
In a region of space, the electric field is pointed along the x-axis, but its magnitude changes as described by
[latex]\begin{array}{c}{E}_{x}=\left(10\phantom{\rule{0.2em}{0ex}}\text{N/C}\right)\phantom{\rule{0.2em}{0ex}}\text{sin}\phantom{\rule{0.2em}{0ex}}\left(20x-500t\right)\hfill \\ {E}_{y}={E}_{z}=0\hfill \end{array}[/latex]
where t is in nanoseconds and x is in cm. Find the displacement current through a circle of radius 3 cm in the [latex]x=0[/latex] plane at [latex]t=0[/latex].
Show Solution
[latex]{I}_{\text{d}}=\left(10\phantom{\rule{0.2em}{0ex}}\text{N/C}\right)\left(8.845\phantom{\rule{0.2em}{0ex}}×\phantom{\rule{0.2em}{0ex}}{10}^{-12}{\phantom{\rule{0.2em}{0ex}}\text{C}}^{2}\text{/N}·{\text{m}}^{2}\right)\text{π}{\left(0.03\phantom{\rule{0.2em}{0ex}}\text{m}\right)}^{2}\left(5000\frac{1}{\text{s}}\right)=1.25\phantom{\rule{0.2em}{0ex}}×\phantom{\rule{0.2em}{0ex}}{10}^{-9}\phantom{\rule{0.2em}{0ex}}\text{A}[/latex]
A microwave oven uses electromagnetic waves of frequency [latex]f=2.45\phantom{\rule{0.2em}{0ex}}×\phantom{\rule{0.2em}{0ex}}{10}^{9}\phantom{\rule{0.2em}{0ex}}\text{Hz}[/latex] to heat foods. The waves reflect from the inside walls of the oven to produce an interference pattern of standing waves whose antinodes are hot spots that can leave observable pit marks in some foods. The pit marks are measured to be 6.0 cm apart. Use the method employed by Heinrich Hertz to calculate the speed of electromagnetic waves this implies.
Use the Appendix D for the next two exercises
Galileo proposed measuring the speed of light by uncovering a lantern and having an assistant a known distance away uncover his lantern when he saw the light from Galileo’s lantern, and timing the delay. How far away must the assistant be for the delay to equal the human reaction time of about 0.25 s?
Show Solution
[latex]3.75\phantom{\rule{0.2em}{0ex}}×\phantom{\rule{0.2em}{0ex}}{10}^{7}\phantom{\rule{0.2em}{0ex}}\text{km}[/latex], which is much greater than Earth’s circumference
Show that the wave equation in one dimension
[latex]\frac{{\partial }^{2}f}{\partial {x}^{2}}=\frac{1}{{v}^{2}}\phantom{\rule{0.2em}{0ex}}\frac{{\partial }^{2}f}{\partial {t}^{2}}[/latex]
is satisfied by any doubly differentiable function of either the form [latex]f\left(x-vt\right)[/latex] or [latex]f\left(x+vt\right)[/latex].
On its highest power setting, a microwave oven increases the temperature of 0.400 kg of spaghetti by [latex]45.0\phantom{\rule{0.2em}{0ex}}\text{°}\text{C}[/latex] in 120 s. (a) What was the rate of energy absorption by the spaghetti, given that its specific heat is [latex]3.76\phantom{\rule{0.2em}{0ex}}×\phantom{\rule{0.2em}{0ex}}{10}^{3}\phantom{\rule{0.2em}{0ex}}\text{J/kg}·\text{°}\text{C}[/latex] ? Assume the spaghetti is perfectly absorbing. (b) Find the average intensity of the microwaves, given that they are absorbed over a circular area 20.0 cm in diameter. (c) What is the peak electric field strength of the microwave? (d) What is its peak magnetic field strength?
Show Solution
a. 564 W; b. [latex]1.80\phantom{\rule{0.2em}{0ex}}×\phantom{\rule{0.2em}{0ex}}{10}^{4}{\phantom{\rule{0.2em}{0ex}}\text{W/m}}^{2}[/latex]; c. [latex]3.68\phantom{\rule{0.2em}{0ex}}×\phantom{\rule{0.2em}{0ex}}{10}^{3}\phantom{\rule{0.2em}{0ex}}\text{V/m}[/latex]; d. [latex]1.23\phantom{\rule{0.2em}{0ex}}×\phantom{\rule{0.2em}{0ex}}{10}^{-5}\phantom{\rule{0.2em}{0ex}}\text{T}[/latex]
A certain microwave oven projects 1.00 kW of microwaves onto a 30-cm-by-40-cm area. (a) What is its intensity in [latex]{\text{W/m}}^{2}[/latex] ? (b) Calculate the maximum electric field strength [latex]{E}_{0}[/latex] in these waves. (c) What is the maximum magnetic field strength [latex]{B}_{0}[/latex] ?
Electromagnetic radiation from a 5.00-mW laser is concentrated on a [latex]1.00{\text{-mm}}^{2}[/latex] area. (a) What is the intensity in [latex]{\text{W/m}}^{2}[/latex] ? (b) Suppose a 2.00-nC electric charge is in the beam. What is the maximum electric force it experiences? (c) If the electric charge moves at 400 m/s, what maximum magnetic force can it feel?
Show Solution
a. [latex]5.00\phantom{\rule{0.2em}{0ex}}×\phantom{\rule{0.2em}{0ex}}{10}^{3}{\phantom{\rule{0.2em}{0ex}}\text{W/m}}^{2}[/latex]; b. [latex]3.88\phantom{\rule{0.2em}{0ex}}×\phantom{\rule{0.2em}{0ex}}{10}^{\text{−}6}\phantom{\rule{0.2em}{0ex}}\text{N}[/latex]; c. [latex]5.18\phantom{\rule{0.2em}{0ex}}×\phantom{\rule{0.2em}{0ex}}{10}^{\text{−}12}\phantom{\rule{0.2em}{0ex}}\text{N}[/latex]
A 200-turn flat coil of wire 30.0 cm in diameter acts as an antenna for FM radio at a frequency of 100 MHz. The magnetic field of the incoming electromagnetic wave is perpendicular to the coil and has a maximum strength of [latex]1.00\phantom{\rule{0.2em}{0ex}}×\phantom{\rule{0.2em}{0ex}}{10}^{-12}\phantom{\rule{0.2em}{0ex}}\text{T}[/latex]. (a) What power is incident on the coil? (b) What average emf is induced in the coil over one-fourth of a cycle? (c) If the radio receiver has an inductance of [latex]2.50\phantom{\rule{0.2em}{0ex}}\mu \text{H}[/latex], what capacitance must it have to resonate at 100 MHz?
Suppose a source of electromagnetic waves radiates uniformly in all directions in empty space where there are no absorption or interference effects. (a) Show that the intensity is inversely proportional to [latex]{r}^{2}[/latex], the distance from the source squared. (b) Show that the magnitudes of the electric and magnetic fields are inversely proportional to r.
Show Solution
a. [latex]I=\frac{P}{A}=\frac{P}{4\pi {r}^{2}}\propto \frac{1}{{r}^{2}}[/latex]; b. [latex]I\propto {E}_{0}^{2}\phantom{\rule{0.2em}{0ex}},\phantom{\rule{0.2em}{0ex}}{B}_{0}^{2}⇒{E}_{0}^{2}\phantom{\rule{0.2em}{0ex}},\phantom{\rule{0.2em}{0ex}}{B}_{0}^{2}\propto \frac{1}{{r}^{2}}⇒{E}_{0},{B}_{0}\propto \frac{1}{r}[/latex]
A radio station broadcasts its radio waves with a power of 50,000 W. What would be the intensity of this signal if it is received on a planet orbiting Proxima Centuri, the closest star to our Sun, at 4.243 ly away?
The Poynting vector describes a flow of energy whenever electric and magnetic fields are present. Consider a long cylindrical wire of radius r with a current I in the wire, with resistance R and voltage V. From the expressions for the electric field along the wire and the magnetic field around the wire, obtain the magnitude and direction of the Poynting vector at the surface. Show that it accounts for an energy flow into the wire from the fields around it that accounts for the Ohmic heating of the wire.
Show Solution
[latex]\begin{array}{cc}\hfill \text{Power into the wire}& =\int \stackrel{\to }{\textbf{S}}·d\stackrel{\to }{\textbf{A}}=\left(\frac{1}{{\mu }_{0}}EB\right)\left(2\pi rL\right)\hfill \\ & =\frac{1}{{\mu }_{0}}\left(\frac{V}{L}\right)\left(\frac{{\mu }_{0}i}{2\pi r}\right)\left(2\pi rL\right)=iV={i}^{2}R\hfill \end{array}[/latex]
The Sun’s energy strikes Earth at an intensity of [latex]1.37\phantom{\rule{0.2em}{0ex}}{\text{kW/m}}^{2}[/latex]. Assume as a model approximation that all of the light is absorbed. (Actually, about 30% of the light intensity is reflected out into space.)
(a) Calculate the total force that the Sun’s radiation exerts on Earth.
(b) Compare this to the force of gravity between the Sun and Earth.
Earth’s mass is [latex]5.972\phantom{\rule{0.2em}{0ex}}×\phantom{\rule{0.2em}{0ex}}{10}^{24}\phantom{\rule{0.2em}{0ex}}\text{kg}.[/latex]
If a Lightsail spacecraft were sent on a Mars mission, by what ratio of the final force to the initial force would its propulsion be reduced when it reached Mars?
Show Solution
0.431
Lunar astronauts placed a reflector on the Moon’s surface, off which a laser beam is periodically reflected. The distance to the Moon is calculated from the round-trip time. (a) To what accuracy in meters can the distance to the Moon be determined, if this time can be measured to 0.100 ns? (b) What percent accuracy is this, given the average distance to the Moon is 384,400 km?
Radar is used to determine distances to various objects by measuring the round-trip time for an echo from the object. (a) How far away is the planet Venus if the echo time is 1000 s? (b) What is the echo time for a car 75.0 m from a highway police radar unit? (c) How accurately (in nanoseconds) must you be able to measure the echo time to an airplane 12.0 km away to determine its distance within 10.0 m?
Show Solution
a. [latex]1.5\phantom{\rule{0.2em}{0ex}}×\phantom{\rule{0.2em}{0ex}}{10}^{11}\text{m}[/latex]; b. [latex]5.0\phantom{\rule{0.2em}{0ex}}×\phantom{\rule{0.2em}{0ex}}{10}^{-7}\text{s}[/latex]; c. 33 ns
Calculate the ratio of the highest to lowest frequencies of electromagnetic waves the eye can see, given the wavelength range of visible light is from 380 to 760 nm. (Note that the ratio of highest to lowest frequencies the ear can hear is 1000.)
How does the wavelength of radio waves for an AM radio station broadcasting at 1030 KHz compare with the wavelength of the lowest audible sound waves (of 20 Hz). The speed of sound in air at [latex]20\phantom{\rule{0.2em}{0ex}}\text{°C}[/latex] is about 343 m/s.
Show Solution
[latex]\begin{array}{ccc}\hfill \text{sound:}\phantom{\rule{0.2em}{0ex}}{\lambda }_{\text{sound}}& =\hfill & \frac{{v}_{s}}{f}=\frac{343\phantom{\rule{0.2em}{0ex}}\text{m/s}}{20.0\phantom{\rule{0.2em}{0ex}}\text{Hz}}=17.2\phantom{\rule{0.2em}{0ex}}\text{m}\hfill \\ \hfill \text{radio:}\phantom{\rule{0.2em}{0ex}}{\lambda }_{\text{radio}}& =\hfill & \frac{c}{f}=\frac{3.00\phantom{\rule{0.2em}{0ex}}×\phantom{\rule{0.2em}{0ex}}{10}^{8}\phantom{\rule{0.2em}{0ex}}\text{m/s}}{1030\phantom{\rule{0.2em}{0ex}}×\phantom{\rule{0.2em}{0ex}}{10}^{3}\phantom{\rule{0.2em}{0ex}}\text{Hz}}=291\phantom{\rule{0.2em}{0ex}}\text{m; or}\phantom{\rule{0.2em}{0ex}}17.1\phantom{\rule{0.2em}{0ex}}{\lambda }_{\text{sound}}\hfill \end{array}[/latex]
Challenge Problems
A parallel-plate capacitor with plate separation d is connected to a source of emf that places a time-dependent voltage V(t) across its circular plates of radius [latex]{r}_{0}[/latex] and area [latex]A=\pi {r}_{0}^{2}[/latex] (see below).
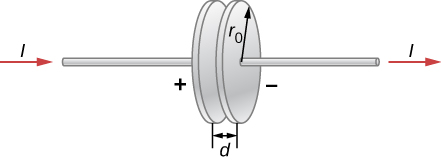
(a) Write an expression for the time rate of change of energy inside the capacitor in terms of V(t) and dV(t)/dt.
(b) Assuming that V(t) is increasing with time, identify the directions of the electric field lines inside the capacitor and of the magnetic field lines at the edge of the region between the plates, and then the direction of the Poynting vector [latex]\stackrel{\to }{\textbf{S}}[/latex] at this location.
(c) Obtain expressions for the time dependence of E(t), for B(t) from the displacement current, and for the magnitude of the Poynting vector at the edge of the region between the plates.
(d) From [latex]\stackrel{\to }{\textbf{S}}[/latex], obtain an expression in terms of V(t) and dV(t)/dt for the rate at which electromagnetic field energy enters the region between the plates.
(e) Compare the results of parts (a) and (d) and explain the relationship between them.
A particle of cosmic dust has a density [latex]\rho =2.0{\phantom{\rule{0.2em}{0ex}}\text{g/cm}}^{3}.[/latex] (a) Assuming the dust particles are spherical and light absorbing, and are at the same distance as Earth from the Sun, determine the particle size for which radiation pressure from sunlight is equal to the Sun’s force of gravity on the dust particle. (b) Explain how the forces compare if the particle radius is smaller. (c) Explain what this implies about the sizes of dust particle likely to be present in the inner solar system compared with outside the Oort cloud.
Show Solution
a. [latex]0.29\phantom{\rule{0.2em}{0ex}}\mu \text{m}[/latex]; b. The radiation pressure is greater than the Sun’s gravity if the particle size is smaller, because the gravitational force varies as the radius cubed while the radiation pressure varies as the radius squared. c. The radiation force outward implies that particles smaller than this are less likely to be near the Sun than outside the range of the Sun’s radiation pressure.
Footnotes
- 1http://earthobservatory.nasa.gov/Features/EnergyBalance/page4.php
Glossary
- gamma ray ([latex]\gamma[/latex] ray)
- extremely high frequency electromagnetic radiation emitted by the nucleus of an atom, either from natural nuclear decay or induced nuclear processes in nuclear reactors and weapons; the lower end of the [latex]\gamma[/latex] -ray frequency range overlaps the upper end of the X-ray range, but [latex]\gamma[/latex] rays can have the highest frequency of any electromagnetic radiation
- infrared radiation
- region of the electromagnetic spectrum with a frequency range that extends from just below the red region of the visible light spectrum up to the microwave region, or from [latex]0.74\phantom{\rule{0.2em}{0ex}}\mu \text{m to}\phantom{\rule{0.2em}{0ex}}300\phantom{\rule{0.2em}{0ex}}\mu \text{m}[/latex]
- microwaves
- electromagnetic waves with wavelengths in the range from 1 mm to 1 m; they can be produced by currents in macroscopic circuits and devices
- radar
- common application of microwaves; radar can determine the distance to objects as diverse as clouds and aircraft, as well as determine the speed of a car or the intensity of a rainstorm
- radio waves
- electromagnetic waves with wavelengths in the range from 1 mm to 100 km; they are produced by currents in wires and circuits and by astronomical phenomena
- thermal agitation
- thermal motion of atoms and molecules in any object at a temperature above absolute zero, which causes them to emit and absorb radiation
- ultraviolet radiation
- electromagnetic radiation in the range extending upward in frequency from violet light and overlapping with the lowest X-ray frequencies, with wavelengths from 400 nm down to about 10 nm
- visible light
- narrow segment of the electromagnetic spectrum to which the normal human eye responds, from about 400 to 750 nm
- X-ray
- invisible, penetrating form of very high frequency electromagnetic radiation, overlapping both the ultraviolet range and the [latex]\gamma[/latex]-ray range
Licenses and Attributions
The Electromagnetic Spectrum. Authored by: OpenStax College. Located at: https://openstax.org/books/university-physics-volume-2/pages/16-5-the-electromagnetic-spectrum. License: CC BY: Attribution. License Terms: Download for free at https://openstax.org/books/university-physics-volume-2/pages/1-introduction

