Chapter 4. The Second Law of Thermodynamics

4.7 Entropy on a Microscopic Scale

Learning Objectives

By the end of this section you will be able to:

  • Interpret the meaning of entropy at a microscopic scale
  • Calculate a change in entropy for an irreversible process of a system and contrast with the change in entropy of the universe
  • Explain the third law of thermodynamics

We have seen how entropy is related to heat exchange at a particular temperature. In this section, we consider entropy from a statistical viewpoint. Although the details of the argument are beyond the scope of this textbook, it turns out that entropy can be related to how disordered or randomized a system is—the more it is disordered, the higher is its entropy. For example, a new deck of cards is very ordered, as the cards are arranged numerically by suit. In shuffling this new deck, we randomize the arrangement of the cards and therefore increase its entropy (Figure 4.17). Thus, by picking one card off the top of the deck, there would be no indication of what the next selected card will be.

The photo shows a person’s hand shuffling a deck of cards.
Figure 4.17 The entropy of a new deck of cards goes up after the dealer shuffles them. (credit: “Rommel SK”/YouTube)

The second law of thermodynamics requires that the entropy of the universe increase in any irreversible process. Thus, in terms of order, the second law may be stated as follows:

In any irreversible process, the universe becomes more disordered. For example, the irreversible free expansion of an ideal gas, shown in Figure 4.2, results in a larger volume for the gas molecules to occupy. A larger volume means more possible arrangements for the same number of atoms, so disorder is also increased. As a result, the entropy of the gas has gone up. The gas in this case is a closed system, and the process is irreversible. Changes in phase also illustrate the connection between entropy and disorder.

Example

Entropy Change of the Universe

Suppose we place 50 g of ice at [latex]0\phantom{\rule{0.2em}{0ex}}\text{°C}[/latex] in contact with a heat reservoir at [latex]20\phantom{\rule{0.2em}{0ex}}\text{°C}[/latex]. Heat spontaneously flows from the reservoir to the ice, which melts and eventually reaches a temperature of [latex]20\phantom{\rule{0.2em}{0ex}}\text{°C}[/latex]. Find the change in entropy of (a) the ice and (b) the universe.

Strategy

Because the entropy of a system is a function of its state, we can imagine two reversible processes for the ice: (1) ice is melted at [latex]0\phantom{\rule{0.2em}{0ex}}\text{°C}\left({T}_{A}\right);[/latex] and (2) melted ice (water) is warmed up from [latex]0\phantom{\rule{0.2em}{0ex}}\text{°C}[/latex] to [latex]20\phantom{\rule{0.2em}{0ex}}\text{°C}\left({T}_{B}\right)[/latex] under constant pressure. Then, we add the change in entropy of the reservoir when we calculate the change in entropy of the universe.

Solution

Show Answer
  1. From Equation 4.10, the increase in entropy of the ice is
[latex]\begin{array}{cc}\text{Δ}{S}_{\text{ice}}\hfill & =\text{Δ}{S}_{1}+\text{Δ}{S}_{2}\hfill \\ & =\frac{m{L}_{f}}{{T}_{A}}+mc{\int }_{A}^{B}\frac{dT}{T}\hfill \\ & =\left(\frac{50\phantom{\rule{0.2em}{0ex}}×\phantom{\rule{0.2em}{0ex}}335}{273}+50\phantom{\rule{0.2em}{0ex}}×\phantom{\rule{0.2em}{0ex}}4.19\phantom{\rule{0.2em}{0ex}}×\phantom{\rule{0.2em}{0ex}}\text{ln}\frac{293}{273}\right)\phantom{\rule{0.2em}{0ex}}\text{J/K}\hfill \\ & =76.3\phantom{\rule{0.2em}{0ex}}\text{J/K}.\hfill \end{array}[/latex]
  • During this transition, the reservoir gives the ice an amount of heat equal to
[latex]\begin{array}{cc}Q\hfill & =m{L}_{f}+mc\left({T}_{B}-{T}_{A}\right)\hfill \\ & =50\phantom{\rule{0.2em}{0ex}}×\phantom{\rule{0.2em}{0ex}}\left(335+4.19\phantom{\rule{0.2em}{0ex}}×\phantom{\rule{0.2em}{0ex}}20\right)\phantom{\rule{0.2em}{0ex}}\text{J}\hfill \\ & =2.10\phantom{\rule{0.2em}{0ex}}×\phantom{\rule{0.2em}{0ex}}{10}^{4}\phantom{\rule{0.2em}{0ex}}\text{J}.\hfill \end{array}[/latex]

This leads to a change (decrease) in entropy of the reservoir:

[latex]\text{Δ}{S}_{\text{reservoir}}=\frac{\text{−}Q}{{T}_{B}}=-71.7\phantom{\rule{0.2em}{0ex}}\text{J/K}.[/latex]

The increase in entropy of the universe is therefore

[latex]\text{Δ}{S}_{\text{universe}}=76.3\phantom{\rule{0.2em}{0ex}}\text{J/K}-71.7\phantom{\rule{0.2em}{0ex}}\text{J/K}=4.6\phantom{\rule{0.2em}{0ex}}\text{J/K}>0.[/latex]

Significance

The entropy of the universe therefore is greater than zero since the ice gains more entropy than the reservoir loses. If we considered only the phase change of the ice into water and not the temperature increase, the entropy change of the ice and reservoir would be the same, resulting in the universe gaining no entropy.

This process also results in a more disordered universe. The ice changes from a solid with molecules located at specific sites to a liquid whose molecules are much freer to move. The molecular arrangement has therefore become more randomized. Although the change in average kinetic energy of the molecules of the heat reservoir is negligible, there is nevertheless a significant decrease in the entropy of the reservoir because it has many more molecules than the melted ice cube. However, the reservoir’s decrease in entropy is still not as large as the increase in entropy of the ice. The increased disorder of the ice more than compensates for the increased order of the reservoir, and the entropy of the universe increases by 4.6 J/K.

You might suspect that the growth of different forms of life might be a net ordering process and therefore a violation of the second law. After all, a single cell gathers molecules and eventually becomes a highly structured organism, such as a human being. However, this ordering process is more than compensated for by the disordering of the rest of the universe. The net result is an increase in entropy and an increase in the disorder of the universe.

Check Your Understanding

In Example 4.7, the spontaneous flow of heat from a hot object to a cold object results in a net increase in entropy of the universe. Discuss how this result can be related to an increase in disorder of the system.

Show Solution

When heat flows from the reservoir to the ice, the internal (mainly kinetic) energy of the ice goes up, resulting in a higher average speed and thus an average greater position variance of the molecules in the ice. The reservoir does become more ordered, but due to its much larger amount of molecules, it does not offset the change in entropy in the system.

The second law of thermodynamics makes clear that the entropy of the universe never decreases during any thermodynamic process. For any other thermodynamic system, when the process is reversible, the change of the entropy is given by [latex]\text{Δ}S=Q\text{/}T[/latex]. But what happens if the temperature goes to zero, [latex]T\to 0[/latex]? It turns out this is not a question that can be answered by the second law.

A fundamental issue still remains: Is it possible to cool a system all the way down to zero kelvin? We understand that the system must be at its lowest energy state because lowering temperature reduces the kinetic energy of the constituents in the system. What happens to the entropy of a system at the absolute zero temperature? It turns out the absolute zero temperature is not reachable—at least, not though a finite number of cooling steps. This is a statement of the third law of thermodynamics, whose proof requires quantum mechanics that we do not present here. In actual experiments, physicists have continuously pushed that limit downward, with the lowest temperature achieved at about [latex]1\phantom{\rule{0.2em}{0ex}}×\phantom{\rule{0.2em}{0ex}}{10}^{-10}\phantom{\rule{0.2em}{0ex}}\text{K}[/latex] in a low-temperature lab at the Helsinki University of Technology in 2008.

Like the second law of thermodynamics, the third law of thermodynamics can be stated in different ways. One of the common statements of the third law of thermodynamics is: The absolute zero temperature cannot be reached through any finite number of cooling steps.

In other words, the temperature of any given physical system must be finite, that is, [latex]T>0[/latex]. This produces a very interesting question in physics: Do we know how a system would behave if it were at the absolute zero temperature?

The reason a system is unable to reach 0 K is fundamental and requires quantum mechanics to fully understand its origin. But we can certainly ask what happens to the entropy of a system when we try to cool it down to 0 K. Because the amount of heat that can be removed from the system becomes vanishingly small, we expect that the change in entropy of the system along an isotherm approaches zero, that is,

[latex]\underset{T\to 0}{\text{lim}}{\left(\text{Δ}S\right)}_{T}=0.[/latex]

This can be viewed as another statement of the third law, with all the isotherms becoming isentropic, or into a reversible ideal adiabat. We can put this expression in words: A system becomes perfectly ordered when its temperature approaches absolute zero and its entropy approaches its absolute minimum.

The third law of thermodynamics puts another limit on what can be done when we look for energy resources. If there could be a reservoir at the absolute zero temperature, we could have engines with efficiency of [latex]100\text{%}[/latex], which would, of course, violate the second law of thermodynamics.

Example

Entropy Change of an Ideal Gas in Free Expansion

An ideal gas occupies a partitioned volume [latex]{V}_{1}[/latex] inside a box whose walls are thermally insulating, as shown in Figure 4.18(a). When the partition is removed, the gas expands and fills the entire volume [latex]{V}_{2}[/latex] of the box, as shown in part (b). What is the entropy change of the universe (the system plus its environment)?

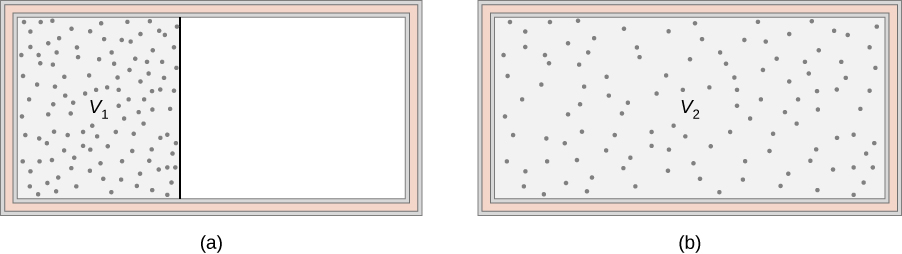
Part a of the figure shows a container which has gas of volume V subscript 1 on the left side and nothing on the right side. Part b shows a container which is completely filled with gas of volume V subscript 2.
Figure 4.18 The adiabatic free expansion of an ideal gas from volume [latex]{V}_{1}[/latex] to volume [latex]{V}_{2}[/latex].

Strategy

The adiabatic free expansion of an ideal gas is an irreversible process. There is no change in the internal energy (and hence temperature) of the gas in such an expansion because no work or heat transfer has happened. Thus, a convenient reversible path connecting the same two equilibrium states is a slow, isothermal expansion from [latex]{V}_{1}[/latex] to [latex]{V}_{2}[/latex]. In this process, the gas could be expanding against a piston while in thermal contact with a heat reservoir, as in step 1 of the Carnot cycle.

Solution

Show Answer

Since the temperature is constant, the entropy change is given by [latex]\text{Δ}S=Q\text{/}T,[/latex] where

[latex]Q=W={\int }_{{V}_{1}}^{{V}_{2}}pdV[/latex]

because [latex]\text{Δ}{E}_{\text{int}}=0.[/latex] Now, with the help of the ideal gas law, we have

[latex]Q=nRT{\int }_{{V}_{1}}^{{V}_{2}}\frac{dV}{V}=nRT\phantom{\rule{0.2em}{0ex}}\text{ln}\frac{{V}_{2}}{{V}_{1}},[/latex]

so the change in entropy of the gas is

[latex]\text{Δ}S=\frac{Q}{T}=nR\phantom{\rule{0.2em}{0ex}}\text{ln}\frac{{V}_{2}}{{V}_{1}}.[/latex]

Because [latex]{V}_{2}>{V}_{1}[/latex], [latex]\text{Δ}S[/latex] is positive, and the entropy of the gas has gone up during the free expansion.

Significance

What about the environment? The walls of the container are thermally insulating, so no heat exchange takes place between the gas and its surroundings. The entropy of the environment is therefore constant during the expansion. The net entropy change of the universe is then simply the entropy change of the gas. Since this is positive, the entropy of the universe increases in the free expansion of the gas.

Example

Entropy Change during Heat Transfer

Heat flows from a steel object of mass 4.00 kg whose temperature is 400 K to an identical object at 300 K. Assuming that the objects are thermally isolated from the environment, what is the net entropy change of the universe after thermal equilibrium has been reached?

Strategy

Since the objects are identical, their common temperature at equilibrium is 350 K. To calculate the entropy changes associated with their transitions, we substitute the irreversible process of the heat transfer by two isobaric, reversible processes, one for each of the two objects. The entropy change for each object is then given by [latex]\text{Δ}S=mc\phantom{\rule{0.2em}{0ex}}\text{ln}\left({T}_{B}\text{/}{T}_{A}\right).[/latex]

Solution

Show Answer

Using [latex]c=450\phantom{\rule{0.2em}{0ex}}\text{J/kg}·\text{K}[/latex], the specific heat of steel, we have for the hotter object

[latex]\begin{array}{cc}\text{Δ}{S}_{\text{h}}\hfill & ={\int }_{{T}_{1}}^{{T}_{2}}\frac{mc\phantom{\rule{0.2em}{0ex}}dT}{T}=mc\phantom{\rule{0.2em}{0ex}}\text{ln}\frac{{T}_{2}}{{T}_{1}}\hfill \\ & =\left(4.00\phantom{\rule{0.2em}{0ex}}\text{kg}\right)\left(450\phantom{\rule{0.2em}{0ex}}\text{J/kg}·\text{K}\right)\text{ln}\frac{350\phantom{\rule{0.2em}{0ex}}\text{K}}{400\phantom{\rule{0.2em}{0ex}}\text{K}}=-240\phantom{\rule{0.2em}{0ex}}\text{J/K}.\hfill \end{array}[/latex]

Similarly, the entropy change of the cooler object is

[latex]\text{Δ}{S}_{\text{c}}=\left(4.00\phantom{\rule{0.2em}{0ex}}\text{kg}\right)\left(450\phantom{\rule{0.2em}{0ex}}\text{J/kg}·\text{K}\right)\phantom{\rule{0.2em}{0ex}}\text{ln}\frac{350\phantom{\rule{0.2em}{0ex}}\text{K}}{300\phantom{\rule{0.2em}{0ex}}\text{K}}=277\phantom{\rule{0.2em}{0ex}}\text{J/K}.[/latex]

The net entropy change of the two objects during the heat transfer is then

[latex]\text{Δ}{S}_{\text{h}}+\text{Δ}{S}_{\text{c}}=37\phantom{\rule{0.2em}{0ex}}\text{J/K}.[/latex]

Significance

The objects are thermally isolated from the environment, so its entropy must remain constant. Thus, the entropy of the universe also increases by 37 J/K.

Check Your Understanding

A quantity of heat Q is absorbed from a reservoir at a temperature [latex]{T}_{\text{h}}[/latex] by a cooler reservoir at a temperature [latex]{T}_{\text{c}}.[/latex] What is the entropy change of the hot reservoir, the cold reservoir, and the universe?

Show Solution

[latex]\text{−}Q\text{/}{T}_{\text{h}}[/latex]; [latex]Q\text{/}{T}_{\text{c}}[/latex]; and [latex]Q\left({T}_{\text{h}}-{T}_{\text{c}}\right)\text{/}\left({T}_{\text{h}}{T}_{\text{c}}\right)[/latex]

Check Your Understanding

A 50-g copper piece at a temperature of [latex]20\phantom{\rule{0.2em}{0ex}}\text{°C}[/latex] is placed into a large insulated vat of water at [latex]100\phantom{\rule{0.2em}{0ex}}\text{°C}[/latex]. (a) What is the entropy change of the copper piece when it reaches thermal equilibrium with the water? (b) What is the entropy change of the water? (c) What is the entropy change of the universe?

Show Solution

a. 4.71 J/K; b. −4.18 J/K; c. 0.53 J/K

View this site to learn about entropy and microstates. Start with a large barrier in the middle and 1000 molecules in only the left chamber. What is the total entropy of the system? Now remove the barrier and let the molecules travel from the left to the right hand side? What is the total entropy of the system now? Lastly, add heat and note what happens to the temperature. Did this increase entropy of the system?

Summary

  • Entropy can be related to how disordered a system is—the more it is disordered, the higher is its entropy. In any irreversible process, the universe becomes more disordered.
  • According to the third law of thermodynamics, absolute zero temperature is unreachable.

Key Equations

Result of energy conservation [latex]W={Q}_{\text{h}}-{Q}_{\text{c}}[/latex]
Efficiency of a heat engine [latex]e=\frac{W}{{Q}_{\text{h}}}=1-\frac{{Q}_{\text{c}}}{{Q}_{\text{h}}}[/latex]
Coefficient of performance of a refrigerator [latex]{K}_{\text{R}}=\frac{{Q}_{\text{c}}}{W}=\frac{{Q}_{\text{c}}}{{Q}_{\text{h}}-{Q}_{\text{c}}}[/latex]
Coefficient of performance of a heat pump [latex]{K}_{\text{P}}=\frac{{Q}_{\text{h}}}{W}=\frac{{Q}_{\text{h}}}{{Q}_{\text{h}}-{Q}_{\text{c}}}[/latex]
Resulting efficiency of a Carnot cycle [latex]e=1-\frac{{T}_{\text{c}}}{{T}_{\text{h}}}[/latex]
Performance coefficient of a reversible refrigerator [latex]{K}_{\text{R}}=\frac{{T}_{\text{c}}}{{T}_{\text{h}}-{T}_{\text{c}}}[/latex]
Performance coefficient of a reversible heat pump [latex]{K}_{\text{P}}=\frac{{T}_{\text{h}}}{{T}_{\text{h}}-{T}_{\text{c}}}[/latex]
Entropy of a system undergoing a reversible process at a constant temperature [latex]\text{Δ}S=\frac{Q}{T}[/latex]
Change of entropy of a system under a reversible process [latex]\text{Δ}S={S}_{B}-{S}_{A}={\int }_{A}^{B}dQ\text{/}T[/latex]
Entropy of a system undergoing any complete reversible cyclic process [latex]\oint dS=\oint \frac{dQ}{T}=0[/latex]
Change of entropy of a closed system under an irreversible process [latex]\text{Δ}S\ge 0[/latex]
Change in entropy of the system along an isotherm [latex]\underset{T\to 0}{\text{lim}}{\left(\text{Δ}S\right)}_{T}=0[/latex]

Conceptual Questions

Are the entropy changes of the systems in the following processes positive or negative? (a) water vapor that condenses on a cold surface; (b) gas in a container that leaks into the surrounding atmosphere; (c) an ice cube that melts in a glass of lukewarm water; (d) the lukewarm water of part (c); (e) a real heat engine performing a cycle; (f) food cooled in a refrigerator.

Discuss the entropy changes in the systems of Question 21.10 in terms of disorder.

Show Solution

Entropy is a function of disorder, so all the answers apply here as well.

Problems

A copper rod of cross-sectional area [latex]5.0\phantom{\rule{0.2em}{0ex}}{\text{cm}}^{2}[/latex] and length 5.0 m conducts heat from a heat reservoir at 373 K to one at 273 K. What is the time rate of change of the universe’s entropy for this process?

Show Solution

[latex]3.78\phantom{\rule{0.2em}{0ex}}×\phantom{\rule{0.2em}{0ex}}{10}^{-3}\phantom{\rule{0.2em}{0ex}}\text{W/K}[/latex]

Fifty grams of water at [latex]20\phantom{\rule{0.2em}{0ex}}\text{°C}[/latex] is heated until it becomes vapor at [latex]100\phantom{\rule{0.2em}{0ex}}\text{°C}[/latex]. Calculate the change in entropy of the water in this process.

Fifty grams of water at [latex]0\phantom{\rule{0.2em}{0ex}}\text{°C}[/latex] are changed into vapor at [latex]100\phantom{\rule{0.2em}{0ex}}\text{°C}[/latex]. What is the change in entropy of the water in this process?

Show Solution

430 J/K

In an isochoric process, heat is added to 10 mol of monoatomic ideal gas whose temperature increases from 273 to 373 K. What is the entropy change of the gas?

Two hundred grams of water at [latex]0\phantom{\rule{0.2em}{0ex}}\text{°C}[/latex] is brought into contact with a heat reservoir at [latex]80\phantom{\rule{0.2em}{0ex}}\text{°C}[/latex]. After thermal equilibrium is reached, what is the temperature of the water? Of the reservoir? How much heat has been transferred in the process? What is the entropy change of the water? Of the reservoir? What is the entropy change of the universe?

Show Solution

[latex]80\phantom{\rule{0.2em}{0ex}}\text{°C}[/latex], [latex]80\phantom{\rule{0.2em}{0ex}}\text{°C}[/latex], [latex]6.70\phantom{\rule{0.2em}{0ex}}×\phantom{\rule{0.2em}{0ex}}{10}^{4}\phantom{\rule{0.2em}{0ex}}\text{J}[/latex], 215 J/K, –190 J/K, 25 J/K

Suppose that the temperature of the water in the previous problem is raised by first bringing it to thermal equilibrium with a reservoir at a temperature of [latex]40\phantom{\rule{0.2em}{0ex}}\text{°C}[/latex] and then with a reservoir at [latex]80\phantom{\rule{0.2em}{0ex}}\text{°C}[/latex]. Calculate the entropy changes of (a) each reservoir, (b) of the water, and (c) of the universe.

Two hundred grams of water at [latex]0\phantom{\rule{0.2em}{0ex}}\text{°C}[/latex] is brought into contact into thermal equilibrium successively with reservoirs at [latex]20\phantom{\rule{0.2em}{0ex}}\text{°C}[/latex], [latex]40\phantom{\rule{0.2em}{0ex}}\text{°C}[/latex], [latex]60\phantom{\rule{0.2em}{0ex}}\text{°C}[/latex], and [latex]80\phantom{\rule{0.2em}{0ex}}\text{°C}[/latex]. (a) What is the entropy change of the water? (b) Of the reservoir? (c) What is the entropy change of the universe?

Show Solution

[latex]\text{Δ}{S}_{{\text{H}}_{2}\text{O}}=215\phantom{\rule{0.2em}{0ex}}\text{J/K}[/latex], [latex]\text{Δ}{S}_{\text{R}}=-208\phantom{\rule{0.2em}{0ex}}\text{J/K}[/latex], [latex]\text{Δ}{S}_{\text{U}}=7\phantom{\rule{0.2em}{0ex}}\text{J/K}[/latex]

(a) Ten grams of [latex]{\text{H}}_{2}\text{O}[/latex] starts as ice at [latex]0\phantom{\rule{0.2em}{0ex}}\text{°C}[/latex]. The ice absorbs heat from the air (just above [latex]0\phantom{\rule{0.2em}{0ex}}\text{°C}[/latex]) until all of it melts. Calculate the entropy change of the [latex]{\text{H}}_{2}\text{O}[/latex], of the air, and of the universe. (b) Suppose that the air in part (a) is at [latex]20\phantom{\rule{0.2em}{0ex}}\text{°C}[/latex] rather than [latex]0\phantom{\rule{0.2em}{0ex}}\text{°C}[/latex] and that the ice absorbs heat until it becomes water at [latex]20\phantom{\rule{0.2em}{0ex}}\text{°C}[/latex]. Calculate the entropy change of the [latex]{\text{H}}_{2}\text{O}[/latex], of the air, and of the universe. (c) Is either of these processes reversible?

The Carnot cycle is represented by the temperature-entropy diagram shown below. (a) How much heat is absorbed per cycle at the high-temperature reservoir? (b) How much heat is exhausted per cycle at the low-temperature reservoir? (c) How much work is done per cycle by the engine? (d) What is the efficiency of the engine?

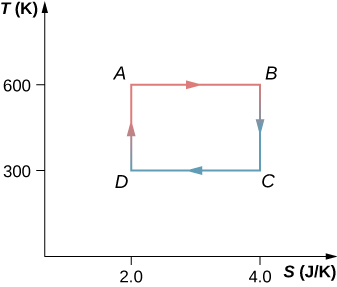
The figure shows a graph with x-axis S in J divided by K and y-axis T in K. The four points A (2.0, 600), B (4.0, 600), C (4.0, 300) ad D (2.0, 300) are connected to form a closed loop.

Show Solution

a. 1200 J; b. 600 J; c. 600 J; d. 0.50

A Carnot engine operating between heat reservoirs at 500 and 300 K absorbs 1500 J per cycle at the high-temperature reservoir. (a) Represent the engine’s cycle on a temperature-entropy diagram. (b) How much work per cycle is done by the engine?

A monoatomic ideal gas (n moles) goes through a cyclic process shown below. Find the change in entropy of the gas in each step and the total entropy change over the entire cycle.

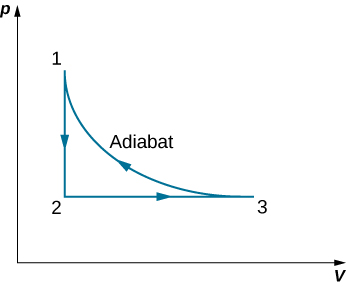
The figure shows a closed loop graph with three points 1, 2 and 3. The x-axis is V and y-axis is p. The value of V at 1 and 2 is equal and the value of p at 2 and 3 is equal.

Show Solution

[latex]\text{Δ}S=n{C}_{V}\phantom{\rule{0.2em}{0ex}}\text{ln}\left(\frac{{T}_{2}}{{T}_{1}}\right)+n{C}_{p}\phantom{\rule{0.2em}{0ex}}\text{ln}\left(\frac{{T}_{3}}{{T}_{2}}\right)[/latex]

A Carnot engine has an efficiency of 0.60. When the temperature of its cold reservoir changes, the efficiency drops to 0.55. If initially [latex]{T}_{\text{c}}=27\phantom{\rule{0.2em}{0ex}}\text{°C}[/latex], determine (a) the constant value of [latex]{T}_{\text{h}}[/latex] and (b) the final value of [latex]{T}_{\text{c}}[/latex].

A Carnot engine performs 100 J of work while discharging 200 J of heat each cycle. After the temperature of the hot reservoir only is adjusted, it is found that the engine now does 130 J of work while discarding the same quantity of heat. (a) What are the initial and final efficiencies of the engine? (b) What is the fractional change in the temperature of the hot reservoir?

Show Solution

a. 0.33, 0.39; b. 0.91

A Carnot refrigerator exhausts heat to the air, which is at a temperature of [latex]25\phantom{\rule{0.2em}{0ex}}\text{°}\text{C}[/latex]. How much power is used by the refrigerator if it freezes 1.5 g of water per second? Assume the water is at [latex]0\phantom{\rule{0.2em}{0ex}}\text{°}\text{C}[/latex].

Additional Problems

A 300-W heat pump operates between the ground, whose temperature is [latex]0\phantom{\rule{0.2em}{0ex}}\text{°}\text{C}[/latex], and the interior of a house at [latex]22\phantom{\rule{0.2em}{0ex}}\text{°C}[/latex]. What is the maximum amount of heat per hour that the heat pump can supply to the house?

Show Solution

[latex]1.45\phantom{\rule{0.2em}{0ex}}×\phantom{\rule{0.2em}{0ex}}{10}^{7}\phantom{\rule{0.2em}{0ex}}\text{J}[/latex]

An engineer must design a refrigerator that does 300 J of work per cycle to extract 2100 J of heat per cycle from a freezer whose temperature is [latex]-10\phantom{\rule{0.2em}{0ex}}\text{°C}[/latex]. What is the maximum air temperature for which this condition can be met? Is this a reasonable condition to impose on the design?

A Carnot engine employs 1.5 mol of nitrogen gas as a working substance, which is considered as an ideal diatomic gas with [latex]\gamma =7.5[/latex] at the working temperatures of the engine. The Carnot cycle goes in the cycle ABCDA with AB being an isothermal expansion. The volume at points A and C of the cycle are [latex]5.0\phantom{\rule{0.2em}{0ex}}×\phantom{\rule{0.2em}{0ex}}{10}^{-3}\phantom{\rule{0.2em}{0ex}}{\text{m}}^{3}[/latex] and 0.15 L, respectively. The engine operates between two thermal baths of temperature 500 K and 300 K. (a) Find the values of volume at B and D. (b) How much heat is absorbed by the gas in the AB isothermal expansion? (c) How much work is done by the gas in the AB isothermal expansion? (d) How much heat is given up by the gas in the CD isothermal expansion? (e) How much work is done by the gas in the CD isothermal compression? (f) How much work is done by the gas in the BC adiabatic expansion? (g) How much work is done by the gas in the DA adiabatic compression? (h) Find the value of efficiency of the engine based on the net work and heat input. Compare this value to the efficiency of a Carnot engine based on the temperatures of the two baths.

Show Solution

a. [latex]{V}_{B}=0.042\phantom{\rule{0.2em}{0ex}}{\text{m}}^{3},{V}_{D}=0.018\phantom{\rule{0.2em}{0ex}}{\text{m}}^{3};[/latex] b. 13,000 J; c. 13,000 J; d. –8,000 J; e. –8,000 J; f. 6200 J; g. –6200 J; h. [latex]39\text{%}[/latex]; with temperatures efficiency is [latex]40\text{%}[/latex], which is off likely by rounding errors.

A 5.0-kg wood block starts with an initial speed of 8.0 m/s and slides across the floor until friction stops it. Estimate the resulting change in entropy of the universe. Assume that everything stays at a room temperature of [latex]20\phantom{\rule{0.2em}{0ex}}\text{°C}[/latex].

A system consisting of 20.0 mol of a monoatomic ideal gas is cooled at constant pressure from a volume of 50.0 L to 10.0 L. The initial temperature was 300 K. What is the change in entropy of the gas?

Show Solution

–670 J/K

A glass beaker of mass 400 g contains 500 g of water at [latex]27\phantom{\rule{0.2em}{0ex}}\text{°}\text{C}[/latex]. The beaker is heated reversibly so that the temperature of the beaker and water rise gradually to [latex]57\phantom{\rule{0.2em}{0ex}}\text{°}\text{C}[/latex]. Find the change in entropy of the beaker and water together.

A Carnot engine operates between [latex]550\phantom{\rule{0.2em}{0ex}}\text{°}\text{C}[/latex] and [latex]20\phantom{\rule{0.2em}{0ex}}\text{°}\text{C}[/latex] baths and produces 300 kJ of energy in each cycle. Find the change in entropy of the (a) hot bath and (b) cold bath, in each Carnot cycle?

Show Solution

a. –570 J/K; b. 570 J/K

An ideal gas at temperature T is stored in the left half of an insulating container of volume V using a partition of negligible volume (see below). What is the entropy change per mole of the gas in each of the following cases? (a) The partition is suddenly removed and the gas quickly fills the entire container. (b) A tiny hole is punctured in the partition and after a long period, the gas reaches an equilibrium state such that there is no net flow through the hole. (c) The partition is moved very slowly and adiabatically all the way to the right wall so that the gas finally fills the entire container.

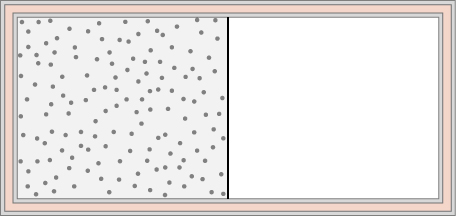
The figure shows a container which is filled with gas on the left half and is empty on the right half.

A 0.50-kg piece of aluminum at [latex]250\phantom{\rule{0.2em}{0ex}}\text{°}\text{C}[/latex] is dropped into 1.0 kg of water at [latex]20\phantom{\rule{0.2em}{0ex}}\text{°}\text{C}[/latex]. After equilibrium is reached, what is the net entropy change of the system?

Show Solution

82 J/K

Suppose 20 g of ice at [latex]0\phantom{\rule{0.2em}{0ex}}\text{°}\text{C}[/latex] is added to 300 g of water at [latex]60\phantom{\rule{0.2em}{0ex}}\text{°}\text{C}[/latex]. What is the total change in entropy of the mixture after it reaches thermal equilibrium?

A heat engine operates between two temperatures such that the working substance of the engine absorbs 5000 J of heat from the high-temperature bath and discharges 3000 J to the low-temperature bath. The rest of the energy is converted into mechanical energy of the turbine. Find (a) the amount of work produced by the engine and (b) the efficiency of the engine.

Show Solution

a. 2000 J; b. [latex]40\text{%}[/latex]

A thermal engine produces 4 MJ of electrical energy while operating between two thermal baths of different temperatures. The working substance of the engine discharges 5 MJ of heat to the cold temperature bath. What is the efficiency of the engine?

A coal power plant consumes 100,000 kg of coal per hour and produces 500 MW of power. If the heat of combustion of coal is 30 MJ/kg, what is the efficiency of the power plant?

Show Solution

[latex]60\text{%}[/latex]

A Carnot engine operates in a Carnot cycle between a heat source at [latex]550\phantom{\rule{0.2em}{0ex}}\text{°}\text{C}[/latex] and a heat sink at [latex]20\phantom{\rule{0.2em}{0ex}}\text{°}\text{C}.[/latex] Find the efficiency of the Carnot engine.

A Carnot engine working between two heat baths of temperatures 600 K and 273 K completes each cycle in 5 sec. In each cycle, the engine absorbs 10 kJ of heat. Find the power of the engine.

Show Solution

[latex]64.4\text{%}[/latex]

A Carnot cycle working between [latex]100\phantom{\rule{0.2em}{0ex}}\text{°}\text{C}[/latex] and [latex]30\phantom{\rule{0.2em}{0ex}}\text{°}\text{C}[/latex] is used to drive a refrigerator between [latex]-10\phantom{\rule{0.2em}{0ex}}\text{°}\text{C}[/latex] and [latex]30\phantom{\rule{0.2em}{0ex}}\text{°}\text{C}.[/latex] How much energy must the Carnot engine produce per second so that the refrigerator is able to discard 10 J of energy per second?

Challenge Problems

(a) An infinitesimal amount of heat is added reversibly to a system. By combining the first and second laws, show that [latex]dU=TdS-dW[/latex]. (b) When heat is added to an ideal gas, its temperature and volume change from [latex]{T}_{1}\phantom{\rule{0.2em}{0ex}}\text{and}\phantom{\rule{0.2em}{0ex}}{V}_{1}\phantom{\rule{0.2em}{0ex}}\text{to}\phantom{\rule{0.2em}{0ex}}{T}_{2}\phantom{\rule{0.2em}{0ex}}\text{and}\phantom{\rule{0.2em}{0ex}}{V}_{2}[/latex]. Show that the entropy change of n moles of the gas is given by

[latex]\text{Δ}S=n{C}_{v}\phantom{\rule{0.2em}{0ex}}\text{ln}\frac{{T}_{2}}{{T}_{1}}+nR\phantom{\rule{0.2em}{0ex}}\text{ln}\frac{{V}_{2}}{{V}_{1}}[/latex].

Show Solution

derive

Using the result of the preceding problem, show that for an ideal gas undergoing an adiabatic process, [latex]T{V}^{\text{γ}-1}[/latex] is constant.

With the help of the two preceding problems, show that [latex]\text{Δ}S[/latex] between states 1 and 2 of n moles an ideal gas is given by

[latex]\text{Δ}S=n{C}_{p}\phantom{\rule{0.2em}{0ex}}\text{ln}\frac{{T}_{2}}{{T}_{1}}-nR\phantom{\rule{0.2em}{0ex}}\text{ln}\frac{{p}_{2}}{{p}_{1}}[/latex].

Show Solution

derive

A cylinder contains 500 g of helium at 120 atm and [latex]20\phantom{\rule{0.2em}{0ex}}\text{°}\text{C}[/latex]. The valve is leaky, and all the gas slowly escapes isothermally into the atmosphere. Use the results of the preceding problem to determine the resulting change in entropy of the universe.

A diatomic ideal gas is brought from an initial equilibrium state at [latex]{p}_{1}=0.50\phantom{\rule{0.2em}{0ex}}\text{atm}[/latex] and [latex]{T}_{1}=300\phantom{\rule{0.2em}{0ex}}\text{K}[/latex] to a final stage with [latex]{p}_{2}=0.20\phantom{\rule{0.2em}{0ex}}\text{atm}[/latex] and [latex]{T}_{1}=500\phantom{\rule{0.2em}{0ex}}\text{K}.[/latex] Use the results of the previous problem to determine the entropy change per mole of the gas.

Show Solution

18 J/K

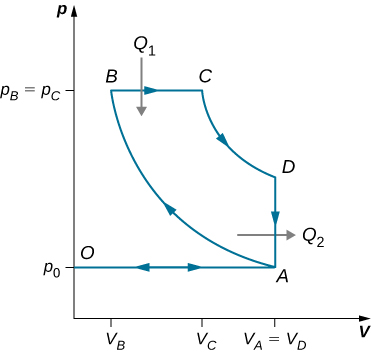
The gasoline internal combustion engine operates in a cycle consisting of six parts. Four of these parts involve, among other things, friction, heat exchange through finite temperature differences, and accelerations of the piston; it is irreversible. Nevertheless, it is represented by the ideal reversible Otto cycle, which is illustrated below. The working substance of the cycle is assumed to be air. The six steps of the Otto cycle are as follows:

  1. Isobaric intake stroke (OA). A mixture of gasoline and air is drawn into the combustion chamber at atmospheric pressure [latex]{p}_{0}[/latex] as the piston expands, increasing the volume of the cylinder from zero to [latex]{V}_{A}[/latex].
  2. Adiabatic compression stroke (AB). The temperature of the mixture rises as the piston compresses it adiabatically from a volume [latex]{V}_{\text{A}}\phantom{\rule{0.2em}{0ex}}\text{to}\phantom{\rule{0.2em}{0ex}}{V}_{\text{B}}[/latex].
  3. Ignition at constant volume (BC). The mixture is ignited by a spark. The combustion happens so fast that there is essentially no motion of the piston. During this process, the added heat [latex]{Q}_{1}[/latex] causes the pressure to increase from [latex]{p}_{B}\phantom{\rule{0.2em}{0ex}}\text{to}\phantom{\rule{0.2em}{0ex}}{p}_{C}[/latex] at the constant volume [latex]{V}_{\text{B}}\left(={V}_{\text{C}}\right)[/latex].
  4. Adiabatic expansion (CD). The heated mixture of gasoline and air expands against the piston, increasing the volume from [latex]{V}_{C}\phantom{\rule{0.2em}{0ex}}\text{to}\phantom{\rule{0.2em}{0ex}}{V}_{D}[/latex]. This is called the power stroke, as it is the part of the cycle that delivers most of the power to the crankshaft.
  5. Constant-volume exhaust (DA). When the exhaust valve opens, some of the combustion products escape. There is almost no movement of the piston during this part of the cycle, so the volume remains constant at [latex]{V}_{A}\left(={V}_{D}\right)[/latex]. Most of the available energy is lost here, as represented by the heat exhaust [latex]{Q}_{2}[/latex].
  6. Isobaric compression (AO). The exhaust valve remains open, and the compression from [latex]{V}_{A}[/latex] to zero drives out the remaining combustion products.

(a) Using (i) [latex]e=W\text{/}{Q}_{1}[/latex]; (ii) [latex]W={Q}_{1}-{Q}_{2}[/latex]; and (iii) [latex]{Q}_{1}=n{C}_{v}\left({T}_{C}-{T}_{B}\right)[/latex], [latex]{Q}_{2}=n{C}_{v}\left({T}_{D}-{T}_{A}\right)[/latex], show that

[latex]e=1-\frac{{T}_{D}-{T}_{A}}{{T}_{C}-{T}_{B}}[/latex].

(b) Use the fact that steps (ii) and (iv) are adiabatic to show that

[latex]e=1-\frac{1}{{r}^{\gamma -1}}[/latex],

where [latex]r={V}_{A}\text{/}{V}_{B}[/latex]. The quantity r is called the compression ratio of the engine.

(c) In practice, r is kept less than around 7. For larger values, the gasoline-air mixture is compressed to temperatures so high that it explodes before the finely timed spark is delivered. This preignition causes engine knock and loss of power. Show that for [latex]r=6[/latex] and [latex]\gamma =1.4[/latex] (the value for air), [latex]e=0.51[/latex], or an efficiency of [latex]51\text{%}.[/latex] Because of the many irreversible processes, an actual internal combustion engine has an efficiency much less than this ideal value. A typical efficiency for a tuned engine is about [latex]25\text{%}\phantom{\rule{0.2em}{0ex}}\text{to}\phantom{\rule{0.2em}{0ex}}30\text{%}[/latex].

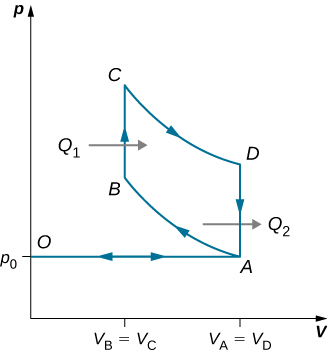
The figure shows a closed loop graph with four points A, B, C and D. The x-axis is V and y-axis is p. The value of V at A and D is equal and at B and C is equal.

An ideal diesel cycle is shown below. This cycle consists of five strokes. In this case, only air is drawn into the chamber during the intake stroke OA. The air is then compressed adiabatically from state A to state B, raising its temperature high enough so that when fuel is added during the power stroke BC, it ignites. After ignition ends at C, there is a further adiabatic power stroke CD. Finally, there is an exhaust at constant volume as the pressure drops from [latex]{p}_{D}[/latex] to [latex]{p}_{A}[/latex], followed by a further exhaust when the piston compresses the chamber volume to zero.

(a) Use [latex]W={Q}_{1}-{Q}_{2}[/latex], [latex]{Q}_{1}=n{C}_{p}\left({T}_{C}-{T}_{B}\right)[/latex], and [latex]{Q}_{2}=n{C}_{v}\left({T}_{D}-{T}_{A}\right)[/latex] to show that [latex]e=\frac{W}{{Q}_{1}}=1-\frac{{T}_{D}-{T}_{A}}{\gamma \left({T}_{C}-{T}_{B}\right)}[/latex].

(b) Use the fact that [latex]A\to B[/latex] and [latex]C\to D[/latex] are adiabatic to show that

[latex]e=1-\frac{1}{\gamma }\phantom{\rule{0.2em}{0ex}}\frac{{\left(\frac{{V}_{C}}{{V}_{D}}\right)}^{\gamma }-{\left(\frac{{V}_{B}}{{V}_{A}}\right)}^{\gamma }}{\left(\frac{{V}_{C}}{{V}_{D}}\right)-\left(\frac{{V}_{B}}{{V}_{A}}\right)}[/latex].

(c) Since there is no preignition (remember, the chamber does not contain any fuel during the compression), the compression ratio can be larger than that for a gasoline engine. Typically, [latex]{V}_{A}\text{/}{V}_{B}=15\phantom{\rule{0.2em}{0ex}}\text{and}\phantom{\rule{0.2em}{0ex}}{V}_{D}\text{/}{V}_{C}=5[/latex]. For these values and [latex]\gamma =1.4,[/latex] show that [latex]\epsilon =0.56[/latex], or an efficiency of [latex]56\text{%}[/latex]. Diesel engines actually operate at an efficiency of about [latex]30\text{%}\phantom{\rule{0.2em}{0ex}}\text{to}\phantom{\rule{0.2em}{0ex}}35\text{%}[/latex] compared with [latex]25\text{%}\phantom{\rule{0.2em}{0ex}}\text{to}\phantom{\rule{0.2em}{0ex}}30\text{%}[/latex] for gasoline engines.

The figure shows a closed loop graph with four points A, B, C and D. The x-axis is V and y-axis is p. The value of V at A and D is equal and the value of p at B and C is equal.

Show Solution

proof

Consider an ideal gas Joule cycle, also called the Brayton cycle, shown below. Find the formula for efficiency of the engine using this cycle in terms of [latex]{P}_{1}[/latex], [latex]{P}_{2}[/latex], and [latex]\gamma[/latex].

The figure shows a closed loop graph with four points 1, 2, 3 and 4. The x-axis is V and y-axis is p. The value of p at 1 and 4 is equal and at 2 and 3 is equal

Derive a formula for the coefficient of performance of a refrigerator using an ideal gas as a working substance operating in the cycle shown below in terms of the properties of the three states labeled 1, 2, and 3.

The figure shows a closed loop graph with three points 1, 2 and 3. The x-axis is V and y-axis is p. The value of V at 1 and 2 is equal and the value of p at 2 and 3 is equal.

Show Solution

[latex]{K}_{\text{R}}=\frac{3\left({p}_{1}-{p}_{2}\right){V}_{1}}{5{p}_{2}{V}_{3}-3{p}_{1}{V}_{1}-{p}_{2}{V}_{1}}[/latex]

Two moles of nitrogen gas, with [latex]\gamma =7\text{/}5[/latex] for ideal diatomic gases, occupies a volume of [latex]{10}^{-2}{\text{m}}^{3}[/latex] in an insulated cylinder at temperature 300 K. The gas is adiabatically and reversibly compressed to a volume of 5 L. The piston of the cylinder is locked in its place, and the insulation around the cylinder is removed. The heat-conducting cylinder is then placed in a 300-K bath. Heat from the compressed gas leaves the gas, and the temperature of the gas becomes 300 K again. The gas is then slowly expanded at the fixed temperature 300 K until the volume of the gas becomes [latex]{10}^{-2}{\text{m}}^{3}[/latex], thus making a complete cycle for the gas. For the entire cycle, calculate (a) the work done by the gas, (b) the heat into or out of the gas, (c) the change in the internal energy of the gas, and (d) the change in entropy of the gas.

A Carnot refrigerator, working between [latex]0\phantom{\rule{0.2em}{0ex}}\text{°}\text{C}[/latex] and [latex]30\phantom{\rule{0.2em}{0ex}}\text{°}\text{C}[/latex] is used to cool a bucket of water containing [latex]{10}^{-2}\phantom{\rule{0.2em}{0ex}}{\text{m}}^{3}[/latex] of water at [latex]30\phantom{\rule{0.2em}{0ex}}\text{°}\text{C}[/latex] to [latex]5\phantom{\rule{0.2em}{0ex}}\text{°}\text{C}[/latex] in 2 hours. Find the total amount of work needed.

Show Solution

[latex]W=110,000\phantom{\rule{0.2em}{0ex}}\text{J}[/latex]

Glossary

disorder
measure of order in a system; the greater the disorder is, the higher the entropy
isentropic
reversible adiabatic process where the process is frictionless and no heat is transferred
third law of thermodynamics
absolute zero temperature cannot be reached through any finite number of cooling steps
Licenses and Attributions

Entropy on a Microscopic Scale. Authored by: OpenStax College. Located at: https://openstax.org/books/university-physics-volume-2/pages/4-7-entropy-on-a-microscopic-scale. License: CC BY: Attribution. License Terms: Download for free at https://openstax.org/books/university-physics-volume-2/pages/1-introduction

License

Icon for the Creative Commons Attribution 4.0 International License

University Physics Volume 2 Copyright © 2016 by cnxuniphysics is licensed under a Creative Commons Attribution 4.0 International License, except where otherwise noted.

Share This Book