Chapter 5. Electric Charges and Fields

5.7 Electric Dipoles

Learning Objectives

By the end of this section, you will be able to:

  • Describe a permanent dipole
  • Describe an induced dipole
  • Define and calculate an electric dipole moment
  • Explain the physical meaning of the dipole moment

Earlier we discussed, and calculated, the electric field of a dipole: two equal and opposite charges that are “close” to each other. (In this context, “close” means that the distance d between the two charges is much, much less than the distance of the field point P, the location where you are calculating the field.) Let’s now consider what happens to a dipole when it is placed in an external field [latex]\stackrel{\to }{\textbf{E}}[/latex]. We assume that the dipole is a permanent dipole; it exists without the field, and does not break apart in the external field.

Rotation of a Dipole due to an Electric Field

For now, we deal with only the simplest case: The external field is uniform in space. Suppose we have the situation depicted in Figure 5.32, where we denote the distance between the charges as the vector [latex]\stackrel{\to }{\textbf{d}},[/latex] pointing from the negative charge to the positive charge. The forces on the two charges are equal and opposite, so there is no net force on the dipole. However, there is a torque:

[latex]\begin{array}{cc}\hfill \stackrel{\to }{\pmb{\tau }}& =\left(\frac{\stackrel{\to }{\textbf{d}}}{2}\phantom{\rule{0.2em}{0ex}}×\phantom{\rule{0.2em}{0ex}}{\stackrel{\to }{\textbf{F}}}_{+}\right)+\left(-\frac{\stackrel{\to }{\textbf{d}}}{2}\phantom{\rule{0.2em}{0ex}}×\phantom{\rule{0.2em}{0ex}}{\stackrel{\to }{\textbf{F}}}_{-}\right)\hfill \\ & =\left[\left(\frac{\stackrel{\to }{\textbf{d}}}{2}\right)\phantom{\rule{0.2em}{0ex}}×\phantom{\rule{0.2em}{0ex}}\left(\text{+}q\stackrel{\to }{\textbf{E}}\right)+\left(-\frac{\stackrel{\to }{\textbf{d}}}{2}\right)\phantom{\rule{0.2em}{0ex}}×\phantom{\rule{0.2em}{0ex}}\left(\text{−}q\stackrel{\to }{\textbf{E}}\right)\right]\hfill \\ & =q\stackrel{\to }{\textbf{d}}\phantom{\rule{0.2em}{0ex}}×\phantom{\rule{0.2em}{0ex}}\stackrel{\to }{\textbf{E}}.\hfill \end{array}[/latex]
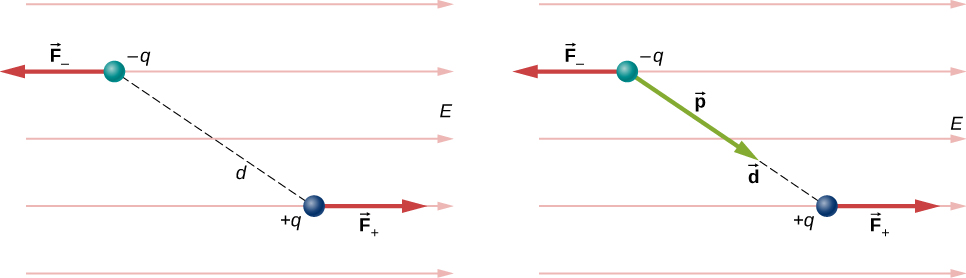
In figure a dipole in a uniform electric field is shown along with the forces on the charges that make up the dipole. The dipole consists of a charge, minus q, and a positive charge, plus q, separated by a distance d. The line connecting the charges is at an angle to the horizontal so that the negative charge is above and to the left of the positive charge. The electric field E is horizontal and points to the right. The force on the negative charge is to the left, and is labeled as F minus. The force on the positive charge is to the right, and is labeled as F plus. Figure b shows the same diagram with the addition of the dipole moment vector, p, which points along the line connecting the charges, from the negative to the positive charge.
Figure 5.32 A dipole in an external electric field. (a) The net force on the dipole is zero, but the net torque is not. As a result, the dipole rotates, becoming aligned with the external field. (b) The dipole moment is a convenient way to characterize this effect. The [latex]\stackrel{\to }{\textbf{d}}[/latex] points in the same direction as [latex]\stackrel{\to }{\textbf{p}}[/latex].

The quantity [latex]q\stackrel{\to }{\textbf{d}}[/latex] (the magnitude of each charge multiplied by the vector distance between them) is a property of the dipole; its value, as you can see, determines the torque that the dipole experiences in the external field. It is useful, therefore, to define this product as the so-called dipole moment of the dipole:

[latex]\stackrel{\to }{\textbf{p}}\equiv q\stackrel{\to }{\textbf{d}}.[/latex]

We can therefore write

[latex]\stackrel{\to }{\pmb{\tau }}=\stackrel{\to }{\textbf{p}}\phantom{\rule{0.2em}{0ex}}×\phantom{\rule{0.2em}{0ex}}\stackrel{\to }{\textbf{E}}.[/latex]

Recall that a torque changes the angular velocity of an object, the dipole, in this case. In this situation, the effect is to rotate the dipole (that is, align the direction of [latex]\stackrel{\to }{\textbf{p}}[/latex]) so that it is parallel to the direction of the external field.

Induced Dipoles

Neutral atoms are, by definition, electrically neutral; they have equal amounts of positive and negative charge. Furthermore, since they are spherically symmetrical, they do not have a “built-in” dipole moment the way most asymmetrical molecules do. They obtain one, however, when placed in an external electric field, because the external field causes oppositely directed forces on the positive nucleus of the atom versus the negative electrons that surround the nucleus. The result is a new charge distribution of the atom, and therefore, an induced dipole moment (Figure 5.33).

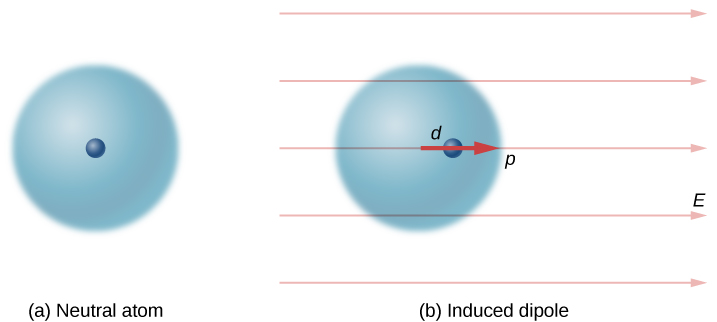
Figure a illustrates a simplified model of a neutral atom. The nucleus is at the center of a uniform sphere negative charge. Figure b shows the atom in a horizontal, uniform electric field, E, that points to the right. The nucleus has shifted to the right a distance d, so that it is no longer at the center of the electron sphere. The result is an induced dipole moment, p, pointing to the right.
Figure 5.33 A dipole is induced in a neutral atom by an external electric field. The induced dipole moment is aligned with the external field.

An important fact here is that, just as for a rotated polar molecule, the result is that the dipole moment ends up aligned parallel to the external electric field. Generally, the magnitude of an induced dipole is much smaller than that of an inherent dipole. For both kinds of dipoles, notice that once the alignment of the dipole (rotated or induced) is complete, the net effect is to decrease the total electric field [latex]{\stackrel{\to }{\textbf{E}}}_{\text{total}}={\stackrel{\to }{\textbf{E}}}_{\text{external}}+{\stackrel{\to }{\textbf{E}}}_{\text{dipole}}[/latex] in the regions inside the dipole charges (Figure 5.34). By “inside” we mean in between the charges. This effect is crucial for capacitors, as you will see in Capacitance.

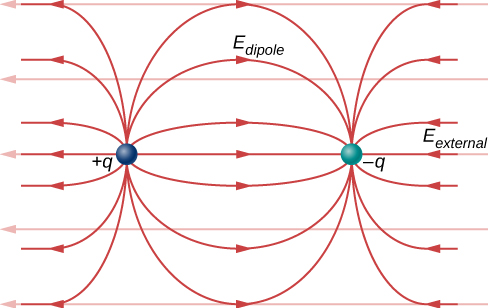
A dipole, consisting of a negative charge on the left and a positive charge on the right is in a uniform electric field pointing to the right. The dipole moment, p, points to the right. The field lines of the net electric field are the sum of the dipole field and the uniform external field, horizontal far from the dipole and similar to the dipole field near the dipole.
Figure 5.34 The net electric field is the vector sum of the field of the dipole plus the external field.

Recall that we found the electric field of a dipole in Equation 5.7. If we rewrite it in terms of the dipole moment we get:

[latex]\stackrel{\to }{\textbf{E}}\left(z\right)=\frac{1}{4\pi {\epsilon }_{0}}\phantom{\rule{0.2em}{0ex}}\frac{\stackrel{\to }{\textbf{p}}}{{z}^{3}}.[/latex]

The form of this field is shown in Figure 5.34. Notice that along the plane perpendicular to the axis of the dipole and midway between the charges, the direction of the electric field is opposite that of the dipole and gets weaker the further from the axis one goes. Similarly, on the axis of the dipole (but outside it), the field points in the same direction as the dipole, again getting weaker the further one gets from the charges.

Summary

  • If a permanent dipole is placed in an external electric field, it results in a torque that aligns it with the external field.
  • If a nonpolar atom (or molecule) is placed in an external field, it gains an induced dipole that is aligned with the external field.
  • The net field is the vector sum of the external field plus the field of the dipole (physical or induced).
  • The strength of the polarization is described by the dipole moment of the dipole, [latex]\stackrel{\to }{\textbf{p}}=q\stackrel{\to }{\textbf{d}}[/latex].

Key Equations

Coulomb’s law [latex]{\stackrel{\to }{\textbf{F}}}_{12}\left(r\right)=\frac{1}{4\pi {\epsilon }_{0}}\phantom{\rule{0.2em}{0ex}}\frac{{q}_{1}{q}_{2}}{{r}_{12}^{2}}{\hat{\textbf{r}}}_{12}[/latex]
Superposition of electric forces [latex]\stackrel{\to }{\textbf{F}}\left(r\right)=\frac{1}{4\pi {\epsilon }_{0}}Q\sum _{i=1}^{N}\frac{{q}_{i}}{{r}_{i}^{2}}{\hat{\textbf{r}}}_{i}[/latex]
Electric force due to an electric field [latex]\stackrel{\to }{\textbf{F}}=Q\stackrel{\to }{\textbf{E}}[/latex]
Electric field at point P [latex]\stackrel{\to }{\textbf{E}}\left(P\right)\equiv \frac{1}{4\pi {\epsilon }_{0}}\sum _{i=1}^{N}\frac{{q}_{i}}{{r}_{i}^{2}}{\hat{\textbf{r}}}_{i}[/latex]
Field of an infinite wire [latex]\stackrel{\to }{\textbf{E}}\left(z\right)=\frac{1}{4\pi {\epsilon }_{0}}\phantom{\rule{0.2em}{0ex}}\frac{2\lambda }{z}\hat{\textbf{k}}[/latex]
Field of an infinite plane [latex]\stackrel{\to }{\textbf{E}}=\frac{\sigma }{2{\epsilon }_{0}}\hat{\textbf{k}}[/latex]
Dipole moment [latex]\stackrel{\to }{\textbf{p}}\equiv q\stackrel{\to }{\textbf{d}}[/latex]
Torque on dipole in external E-field [latex]\stackrel{\to }{\pmb{\tau }}=\stackrel{\to }{\textbf{p}}\phantom{\rule{0.2em}{0ex}}×\phantom{\rule{0.2em}{0ex}}\stackrel{\to }{\textbf{E}}[/latex]

Conceptual Questions

What are the stable orientation(s) for a dipole in an external electric field? What happens if the dipole is slightly perturbed from these orientations?

Problems

Consider the equal and opposite charges shown below. (a) Show that at all points on the x-axis for which [latex]|x|\gg a,E\approx {Qa\text{/}2\pi \epsilon }_{0}{x}^{3}.[/latex] (b) Show that at all points on the y-axis for which [latex]|y|\gg a,E\approx {Qa\text{/}\pi \epsilon }_{0}{y}^{3}.[/latex]

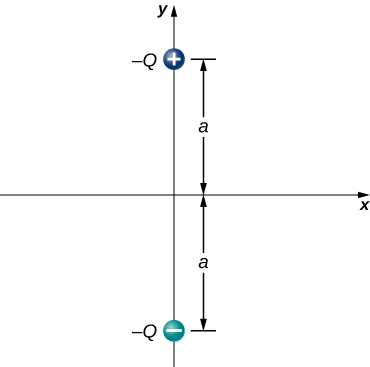
Two charges are shown on the y axis of an x y coordinate system. Charge +Q is a distance a above the origin, and charge −Q is a distance a below the origin.

Show Solution

[latex]{E}_{x}=0,[/latex]
[latex]{E}_{y}=\frac{1}{4\pi {\epsilon }_{0}}\left[\frac{2q}{\left({x}^{2}+{a}^{2}\right)}\phantom{\rule{0.2em}{0ex}}\frac{a}{\sqrt{\left({x}^{2}+{a}^{2}\right)}}\right][/latex]
[latex]⇒x\gg a⇒\frac{1}{2\pi {\epsilon }_{0}}\phantom{\rule{0.2em}{0ex}}\frac{qa}{{x}^{3}}[/latex],
[latex]{E}_{y}=\frac{q}{4\pi {\epsilon }_{0}}\left[\frac{2ya+2ya}{{\left(y-a\right)}^{2}{\left(y+a\right)}^{2}}\right][/latex]
[latex]⇒y\gg a⇒\frac{1}{\pi {\epsilon }_{0}}\phantom{\rule{0.2em}{0ex}}\frac{qa}{{y}^{3}}[/latex]

(a) What is the dipole moment of the configuration shown above? If [latex]Q=4.0\phantom{\rule{0.2em}{0ex}}\mu \text{C}[/latex], (b) what is the torque on this dipole with an electric field of [latex]4.0\phantom{\rule{0.2em}{0ex}}×\phantom{\rule{0.2em}{0ex}}{10}^{5}\phantom{\rule{0.2em}{0ex}}\text{N/C}\hat{\textbf{i}}[/latex]? (c) What is the torque on this dipole with an electric field of [latex]-4.0\phantom{\rule{0.2em}{0ex}}×\phantom{\rule{0.2em}{0ex}}{10}^{5}\phantom{\rule{0.2em}{0ex}}\text{N/C}\hat{\textbf{i}}[/latex]? (d) What is the torque on this dipole with an electric field of [latex]±4.0\phantom{\rule{0.2em}{0ex}}×\phantom{\rule{0.2em}{0ex}}{10}^{5}\phantom{\rule{0.2em}{0ex}}\text{N/C}\hat{\textbf{j}}[/latex]?

A water molecule consists of two hydrogen atoms bonded with one oxygen atom. The bond angle between the two hydrogen atoms is [latex]104\text{°}[/latex] (see below). Calculate the net dipole moment of a water molecule that is placed in a uniform, horizontal electric field of magnitude [latex]2.3\phantom{\rule{0.2em}{0ex}}×\phantom{\rule{0.2em}{0ex}}{10}^{-8}\phantom{\rule{0.2em}{0ex}}\text{N/C}.[/latex] (You are missing some information for solving this problem; you will need to determine what information you need, and look it up.)

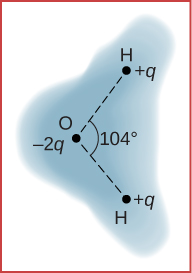
A schematic representation of the outer electron cloud of a neutral water molecule is shown. Three atoms are at the vertices of a triangle. The hydrogen atom has positive q charge and the oxygen atom has minus two q charge, and the angle between the line joining each hydrogen atom with the oxygen atom is one hundred and four degrees. The cloud density is shown as being greater at the oxygen atom.

Show Solution

The net dipole moment of the molecule is the vector sum of the individual dipole moments between the two O-H. The separation O-H is 0.9578 angstroms:
 [latex]\stackrel{\to }{\textbf{p}}=1.889\phantom{\rule{0.2em}{0ex}}×\phantom{\rule{0.2em}{0ex}}{10}^{-29}\phantom{\rule{0.2em}{0ex}}\text{Cm}\phantom{\rule{0.2em}{0ex}}\hat{\textbf{i}}[/latex]

Additional Problems

Point charges [latex]{q}_{1}=2.0\phantom{\rule{0.2em}{0ex}}\mu \text{C}[/latex] and [latex]{q}_{1}=4.0\phantom{\rule{0.2em}{0ex}}\mu \text{C}[/latex] are located at [latex]{r}_{1}=\left(4.0\hat{\textbf{i}}-2.0\hat{\textbf{j}}+2.0\hat{\textbf{k}}\right)\text{m}[/latex] and [latex]{r}_{2}=\left(8.0\hat{\textbf{i}}+5.0\hat{\textbf{j}}-9.0\hat{\textbf{k}}\right)\text{m}[/latex]. What is the force of [latex]{q}_{2}\phantom{\rule{0.2em}{0ex}}\text{on}\phantom{\rule{0.2em}{0ex}}{q}_{1}?[/latex]

What is the force on the [latex]5.0\text{-}\mu \text{C}[/latex] charge shown below?

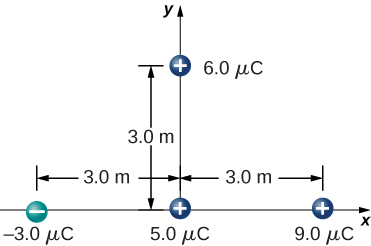
The following charges are shown on an x y coordinate system: Minus 3.0 micro Coulomb on the x axis, 3.0 meters to the left of the origin. Positive 5.0 micro Coulomb at the origin. Positive 9.0 micro Coulomb on the x axis, 3.0 meters to the right of the origin. Positive 6.0 micro Coulomb on the y axis, 3.0 meters above the origin.

Show Solution

[latex]{\stackrel{\to }{\textbf{F}}}_{\text{net}}=\left[-8.99\phantom{\rule{0.2em}{0ex}}×\phantom{\rule{0.2em}{0ex}}{10}^{9}\frac{3.0\phantom{\rule{0.2em}{0ex}}×\phantom{\rule{0.2em}{0ex}}{10}^{-6}\left(5.0\phantom{\rule{0.2em}{0ex}}×\phantom{\rule{0.2em}{0ex}}{10}^{-6}\right)}{{\left(3.0\phantom{\rule{0.2em}{0ex}}\text{m}\right)}^{2}}-8.99\phantom{\rule{0.2em}{0ex}}×\phantom{\rule{0.2em}{0ex}}{10}^{9}\frac{9.0\phantom{\rule{0.2em}{0ex}}×\phantom{\rule{0.2em}{0ex}}{10}^{-6}\left(5.0\phantom{\rule{0.2em}{0ex}}×\phantom{\rule{0.2em}{0ex}}{10}^{-6}\right)}{{\left(3.0\phantom{\rule{0.2em}{0ex}}\text{m}\right)}^{2}}\right]\hat{\textbf{i}}[/latex],
[latex]-8.99\phantom{\rule{0.2em}{0ex}}×\phantom{\rule{0.2em}{0ex}}{10}^{9}\frac{6.0\phantom{\rule{0.2em}{0ex}}×\phantom{\rule{0.2em}{0ex}}{10}^{-6}\left(5.0\phantom{\rule{0.2em}{0ex}}×\phantom{\rule{0.2em}{0ex}}{10}^{-6}\right)}{{\left(3.0\phantom{\rule{0.2em}{0ex}}\text{m}\right)}^{2}}\hat{\textbf{j}}=-0.06\phantom{\rule{0.2em}{0ex}}\text{N}\hat{\textbf{i}}-0.03\phantom{\rule{0.2em}{0ex}}\text{N}\hat{\textbf{j}}[/latex]

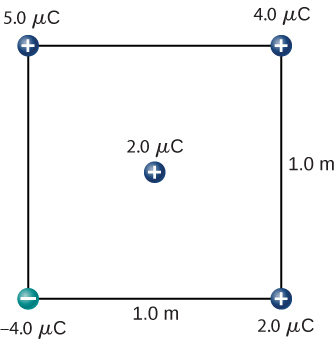
What is the force on the [latex]2.0\text{-}\mu \text{C}[/latex] charge placed at the center of the square shown below?

Charges are shown at the corners of a square with sides length 1 meter. The top left charge is positive 5.0 micro Coulombs. The top right charge is positive 4.0 micro Coulombs. The bottom left charge is negative 4.0 micro Coulombs. The bottom right charge is positive 2.0 micro Coulombs. A fifth charge of positive 2.0 micro Coulombs is at the center of the square.

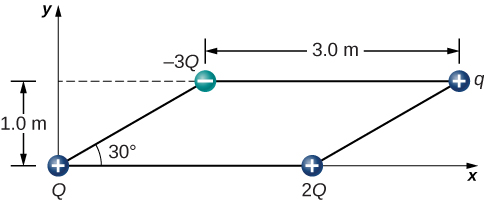
Four charged particles are positioned at the corners of a parallelogram as shown below. If [latex]q=5.0\phantom{\rule{0.2em}{0ex}}\mu \text{C}[/latex] and [latex]Q=8.0\phantom{\rule{0.2em}{0ex}}\mu \text{C},[/latex] what is the net force on q?

Four charges are positioned at the corners of a parallelogram. The top and bottom of the parallelogram are horizontal and are 3.0 meters long. The sides are at a thirty degree angle to the x axis. The vertical height of the parallelogram is 1.0 meter. The charges are a positive Q in the lower left corner, positive 2 Q in the lower right corner, negative 3 Q in the upper left corner, and positive q in the upper right corner.

Show Solution

Charges Q and q form a right triangle of sides 1 m and [latex]3+\sqrt{3}\phantom{\rule{0.2em}{0ex}}\text{m}.[/latex] Charges 2Q and q form a right triangle of sides 1 m and [latex]\sqrt{3}\phantom{\rule{0.2em}{0ex}}\text{m}.[/latex]
 [latex]\begin{array}{cc}{F}_{x}\hfill & =0.049\phantom{\rule{0.2em}{0ex}}\text{N},\hfill \end{array}[/latex]
 [latex]{F}_{y}=0.093\phantom{\rule{0.2em}{0ex}}\text{N}[/latex],
 [latex]{\stackrel{\to }{\textbf{F}}}_{\text{net}}=0.036\phantom{\rule{0.2em}{0ex}}\text{N}\phantom{\rule{0.2em}{0ex}}\hat{\textbf{i}}+0.09\phantom{\rule{0.2em}{0ex}}\text{N}\phantom{\rule{0.2em}{0ex}}\hat{\textbf{j}}[/latex]

A charge Q is fixed at the origin and a second charge q moves along the x-axis, as shown below. How much work is done on q by the electric force when q moves from [latex]{x}_{1}\phantom{\rule{0.2em}{0ex}}\text{to}\phantom{\rule{0.2em}{0ex}}{x}_{2}?[/latex]

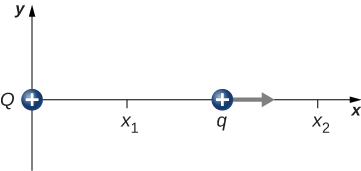
A charge Q is shown at the origin and a second charge q is shown to its right, on the x axis, moving to the right. Both are positive charges. Point x 1 is between the charges. Point x 2 is to the right of both.

A charge [latex]q=-2.0\phantom{\rule{0.2em}{0ex}}\mu \text{C}[/latex] is released from rest when it is 2.0 m from a fixed charge [latex]Q=6.0\phantom{\rule{0.2em}{0ex}}\mu \text{C}.[/latex] What is the kinetic energy of q when it is 1.0 m from Q?

Show Solution

[latex]W=0.054\phantom{\rule{0.2em}{0ex}}\text{J}[/latex]

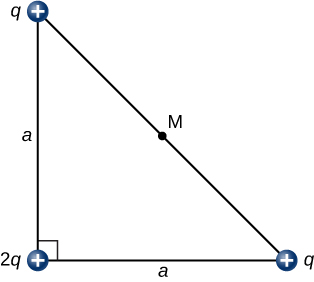
What is the electric field at the midpoint M of the hypotenuse of the triangle shown below?

Charges are shown at the vertices of an isosceles right triangle whose sides are length a and those hypotenuse is length M. The right angle is the bottom right corner. The charge at the right angle is positive 2 q. Both of the other two charges are positive q.

Find the electric field at P for the charge configurations shown below.

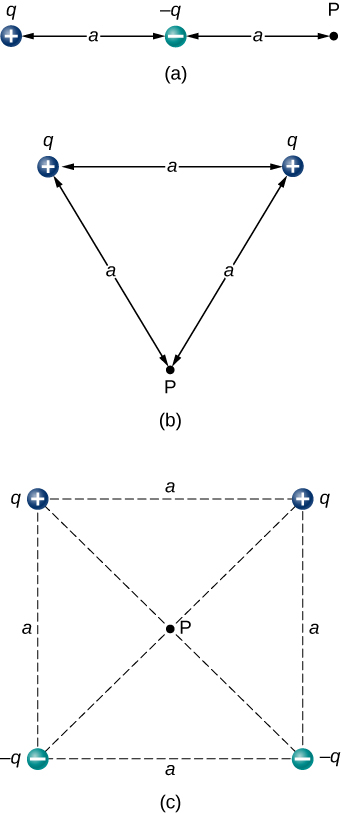
In figure a, positive charge q is on the left, negative charge q is a distance a to the right of it. Point P is a distance a to the right of the negative charge q. In figure b, positive charge q is on the left, and a positive charge q is a distance a to the right of it. Point P is below the midpoint, a distance a from each of the charges so that the two charges and point P are at the vertices of an equilateral triangle whose sides are length a. In figure c, four charges are at the corners of a square whose sides are length a. The two top corners each have positive charge q. The two bottom corners each have negative charge q. Point P is at the center of the square.

Show Solution

a. [latex]\stackrel{\to }{\textbf{E}}=\frac{1}{4\pi {\epsilon }_{0}}\left(\frac{q}{{\left(2a\right)}^{2}}-\frac{q}{{a}^{2}}\right)\hat{\textbf{i}}[/latex]; b. [latex]\stackrel{\to }{\textbf{E}}=\frac{\sqrt{3}}{4\pi {\epsilon }_{0}}\phantom{\rule{0.2em}{0ex}}\frac{q}{{a}^{2}}\left(\text{−}\hat{\textbf{j}}\right)[/latex]; c. [latex]\stackrel{\to }{\textbf{E}}=\frac{2}{\pi {\epsilon }_{0}}\phantom{\rule{0.2em}{0ex}}\frac{q}{{a}^{2}}\phantom{\rule{0.2em}{0ex}}\frac{1}{\sqrt{2}}\left(\text{−}\hat{\textbf{j}}\right)[/latex]

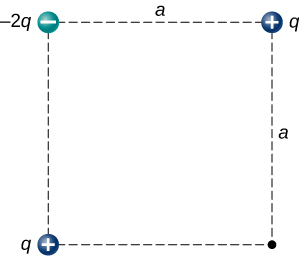
(a) What is the electric field at the lower-right-hand corner of the square shown below? (b) What is the force on a charge q placed at that point?

A square with sides of length a is shown. Three charges are shown as follows: At the top left, a charge of negative 2 q. At the top right, a charge of positive q. At the lower left, a charge of positive q.

Point charges are placed at the four corners of a rectangle as shown below: [latex]{q}_{1}=2.0\phantom{\rule{0.2em}{0ex}}×\phantom{\rule{0.2em}{0ex}}{10}^{-6}\phantom{\rule{0.2em}{0ex}}\text{C},[/latex] [latex]{q}_{2}=-2.0\phantom{\rule{0.2em}{0ex}}×\phantom{\rule{0.2em}{0ex}}{10}^{-6}\phantom{\rule{0.2em}{0ex}}\text{C,}[/latex] [latex]{q}_{3}=4.0\phantom{\rule{0.2em}{0ex}}×\phantom{\rule{0.2em}{0ex}}{10}^{-6}\phantom{\rule{0.2em}{0ex}}\text{C,}[/latex] and [latex]{q}_{4}=1.0\phantom{\rule{0.2em}{0ex}}×\phantom{\rule{0.2em}{0ex}}{10}^{-6}\phantom{\rule{0.2em}{0ex}}\text{C}.[/latex] What is the electric field at P?

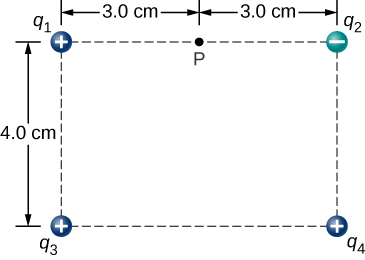
A rectangle is shown with a charge at each corner. The rectangle is 4.0 centimeters high and 6.0 centimeters wide. At the top left is a positive charge q 1. At the top right is a negative charge q 2. At the lower left is a positive charge q 3. At the lower right is a positive charge q 4. Point P is in the middle of the upper edge, 3.0 centimeters to the right of q 1 and 3.0 centimeters to the left of q 2.

Show Solution

[latex]{\stackrel{\to }{\textbf{E}}}_{\text{net}}={\stackrel{\to }{\textbf{E}}}_{1}+{\stackrel{\to }{\textbf{E}}}_{2}+{\stackrel{\to }{\textbf{E}}}_{3}+{\stackrel{\to }{\textbf{E}}}_{4}=\left(4.65\hat{\textbf{i}}+1.44\hat{\textbf{j}}\right)×{10}^{7}N/C[/latex]

Three charges are positioned at the corners of a parallelogram as shown below. (a) If [latex]Q=8.0\phantom{\rule{0.2em}{0ex}}\mu \text{C},[/latex] what is the electric field at the unoccupied corner? (b) What is the force on a [latex]5.0\text{-}\mu \text{C}[/latex] charge placed at this corner?

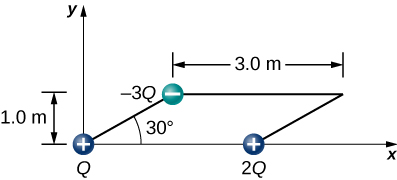
Three charges are positioned at the corners of a parallelogram. The top and bottom of the parallelogram are horizontal and are 3.0 meters long. The sides are at a thirty degree angle to the x axis. The vertical height of the parallelogram is 1.0 meter. The charges are a positive Q in the lower left corner, positive 2 Q in the lower right corner, and negative 3 Q in the upper left corner.

A positive charge q is released from rest at the origin of a rectangular coordinate system and moves under the influence of the electric field [latex]\stackrel{\to }{\textbf{E}}={E}_{0}\left(1+x\text{/}a\right)\hat{\textbf{i}}.[/latex] What is the kinetic energy of q when it passes through [latex]x=3a?[/latex]

Show Solution

[latex]F=q{E}_{0}\left(1+x\text{/}a\right)\phantom{\rule{0.5em}{0ex}}W=\frac{1}{2}m\left({v}^{2}-{v}_{0}^{2}\right)[/latex],
[latex]\frac{1}{2}m{v}^{2}=q{E}_{0}\left(\frac{15a}{2}\right)\phantom{\rule{0.2em}{0ex}}\text{J}[/latex]

A particle of charge [latex]\text{−}q[/latex] and mass m is placed at the center of a uniformaly charged ring of total charge Q and radius R. The particle is displaced a small distance along the axis perpendicular to the plane of the ring and released. Assuming that the particle is constrained to move along the axis, show that the particle oscillates in simple harmonic motion with a frequency [latex]f=\frac{1}{2\pi }\sqrt{\frac{qQ}{4\pi {\epsilon }_{0}m{R}^{3}}}.[/latex]

Charge is distributed uniformly along the entire y-axis with a density [latex]{\lambda }_{y}[/latex] and along the positive x-axis from [latex]x=a\phantom{\rule{0.2em}{0ex}}\text{to}\phantom{\rule{0.2em}{0ex}}x=b[/latex] with a density [latex]{\lambda }_{x}.[/latex] What is the force between the two distributions?

Show Solution

Electric field of wire at x: [latex]\stackrel{\to }{\textbf{E}}\left(x\right)=\frac{1}{4\pi {\epsilon }_{0}}\phantom{\rule{0.2em}{0ex}}\frac{2{\lambda }_{y}}{x}\hat{\textbf{i}}[/latex],
 [latex]dF=\frac{{\lambda }_{y}{\lambda }_{x}}{2\pi {\epsilon }_{0}}\left(\text{ln}\phantom{\rule{0.2em}{0ex}}b-\text{ln}\phantom{\rule{0.2em}{0ex}}a\right)[/latex]

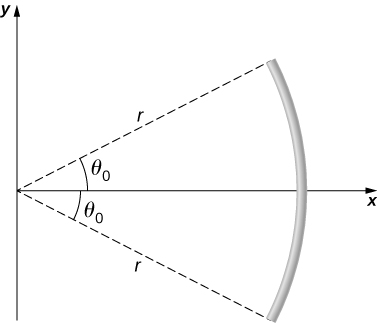
The circular arc shown below carries a charge per unit length [latex]\lambda ={\lambda }_{0}\phantom{\rule{0.2em}{0ex}}\text{cos}\phantom{\rule{0.2em}{0ex}}\theta ,[/latex] where [latex]\theta[/latex] is measured from the x-axis. What is the electric field at the origin?

An arc that is part of a circle of radius r and with center at the origin of an x y coordinate system is shown. The arc extends from an angle theta sub zero above the x axis to an angle theta sub zero below the x axis.

Calculate the electric field due to a uniformly charged rod of length L, aligned with the x-axis with one end at the origin; at a point P on the z-axis.

Show Solution

 

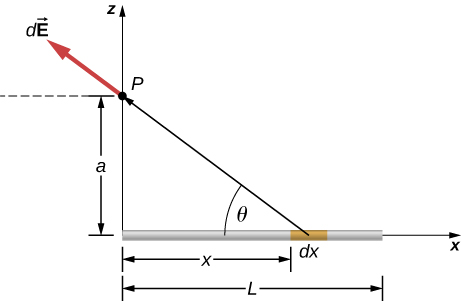
A rod of length L is shown, aligned with the x-axis with the left end at the origin. A point P is shown on the z axis, a distance a above the left end of the rod. A small segment of the rod is labeled as d x and is a distance x to the right of the left end of the rod. The line from dx to point P makes an angle of theta with the x axis. The vector d E, drawn with its tail at point P, points away from the segment d x.

[latex]d{E}_{x}=\frac{1}{4\pi {\epsilon }_{0}}\phantom{\rule{0.2em}{0ex}}\frac{\lambda dx}{\left({x}^{2}+{a}^{2}\right)}\phantom{\rule{0.2em}{0ex}}\frac{x}{\sqrt{{x}^{2}+{a}^{2}}}[/latex],
[latex]{\stackrel{\to }{\textbf{E}}}_{x}=\frac{\lambda }{4\pi {\epsilon }_{0}}\left[\frac{1}{\sqrt{{L}^{2}+{a}^{2}}}-\frac{1}{a}\right]\hat{\textbf{i}}[/latex],
[latex]d{E}_{z}=\frac{1}{4\pi {\epsilon }_{0}}\phantom{\rule{0.2em}{0ex}}\frac{\lambda dx}{\left({x}^{2}+{a}^{2}\right)}\phantom{\rule{0.2em}{0ex}}\frac{a}{\sqrt{{x}^{2}+{a}^{2}}}[/latex],
[latex]{\stackrel{\to }{\textbf{E}}}_{z}=\frac{\lambda }{4\pi {\epsilon }_{0}a}\phantom{\rule{0.2em}{0ex}}\frac{L}{\sqrt{{L}^{2}+{a}^{2}}}\hat{\textbf{k}}[/latex],
 Substituting z for a, we have:
 [latex]\stackrel{\to }{\textbf{E}}\left(z\right)=\frac{\lambda }{4\pi {\epsilon }_{0}}\left[\frac{1}{\sqrt{{L}^{2}+{z}^{2}}}-\frac{1}{z}\right]\hat{\textbf{i}}+\frac{\lambda }{4\pi {\epsilon }_{0}z}\phantom{\rule{0.2em}{0ex}}\frac{L}{\sqrt{{L}^{2}+{z}^{2}}}\hat{\textbf{k}}[/latex]

The charge per unit length on the thin rod shown below is [latex]\lambda .[/latex] What is the electric force on the point charge q? Solve this problem by first considering the electric force [latex]d\stackrel{\to }{\textbf{F}}[/latex] on q due to a small segment [latex]dx[/latex] of the rod, which contains charge [latex]\lambda dx.[/latex] Then, find the net force by integrating [latex]d\stackrel{\to }{\textbf{F}}[/latex] over the length of the rod.

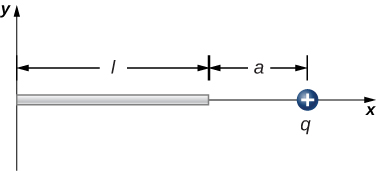
A rod of length l is shown. The rod lies on the horizontal axis, with its left end at the origin. A positive charge q is on the x axis, a distance a to the right of the right end of the rod.

The charge per unit length on the thin rod shown here is [latex]\lambda .[/latex] What is the electric force on the point charge q? (See the preceding problem.)

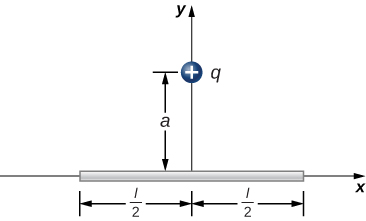
A rod of length l is shown. The rod lies on the horizontal axis, with its center at the origin, so the ends are a distance of l over 2 to the left and right of the origin. A positive charge q is on the y axis, a distance a to above the origin.

Show Solution

There is a net force only in the y-direction. Let [latex]\theta[/latex] be the angle the vector from dx to q makes with the x-axis. The components along the x-axis cancel due to symmetry, leaving the y-component of the force.
 [latex]d{F}_{\text{y}}=\frac{1}{4\pi {\epsilon }_{0}}\phantom{\rule{0.2em}{0ex}}\frac{aq\lambda dx}{{\left({x}^{2}+{a}^{2}\right)}^{3\text{/}2}}[/latex],
 [latex]{F}_{y}=\frac{1}{2\pi {\epsilon }_{0}}\phantom{\rule{0.2em}{0ex}}\frac{q\lambda }{a}\left[\frac{l\text{/}2}{{\left({\left(l\text{/}2\right)}^{2}+{a}^{2}\right)}^{1\text{/}2}}\right][/latex]

The charge per unit length on the thin semicircular wire shown below is [latex]\lambda .[/latex] What is the electric force on the point charge q? (See the preceding problems.)

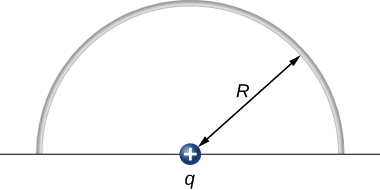
A semicircular arc that the upper half of a circle of radius R is shown. A positive charge q is at the center of the circle.

Glossary

dipole moment
property of a dipole; it characterizes the combination of distance between the opposite charges, and the magnitude of the charges
induced dipole
typically an atom, or a spherically symmetric molecule; a dipole created due to opposite forces displacing the positive and negative charges
permanent dipole
typically a molecule; a dipole created by the arrangement of the charged particles from which the dipole is created
Licenses and Attributions

Electric Dipoles. Authored by: OpenStax College. Located at: https://openstax.org/books/university-physics-volume-2/pages/5-7-electric-dipoles. License: CC BY: Attribution. License Terms: Download for free at https://openstax.org/books/university-physics-volume-2/pages/1-introduction

License

Icon for the Creative Commons Attribution 4.0 International License

University Physics Volume 2 Copyright © 2016 by cnxuniphysics is licensed under a Creative Commons Attribution 4.0 International License, except where otherwise noted.

Share This Book