8.4 Capacitor with a Dielectric

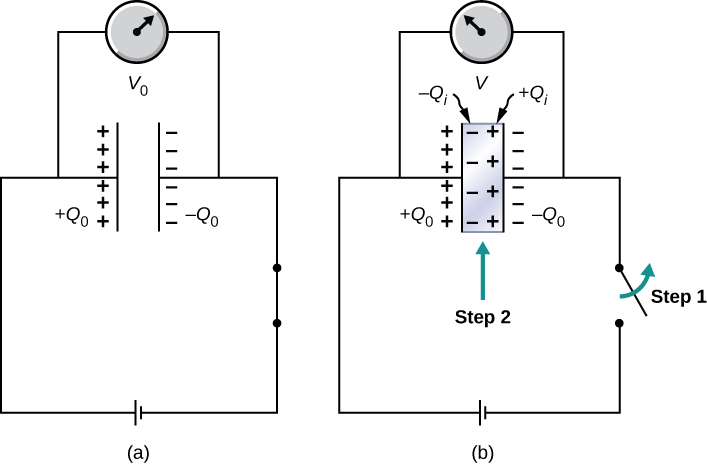
As we discussed earlier, an insulating material placed between the plates of a capacitor is called a dielectric. Inserting a dielectric between the plates of a capacitor affects its capacitance. To see why, let’s consider an experiment described in Figure 8.17. Initially, a capacitor with capacitance [latex]{C}_{0}[/latex] when there is air between its plates is charged by a battery to voltage [latex]{V}_{0}[/latex]. When the capacitor is fully charged, the battery is disconnected. A charge [latex]{Q}_{0}[/latex] then resides on the plates, and the potential difference between the plates is measured to be [latex]{V}_{0}[/latex]. Now, suppose we insert a dielectric that totally fills the gap between the plates. If we monitor the voltage, we find that the voltmeter reading has dropped to a smaller value V. We write this new voltage value as a fraction of the original voltage [latex]{V}_{0}[/latex], with a positive number [latex]\kappa[/latex], [latex]\kappa >1[/latex]:

The constant [latex]\kappa[/latex] in this equation is called the dielectric constant of the material between the plates, and its value is characteristic for the material. A detailed explanation for why the dielectric reduces the voltage is given in the next section. Different materials have different dielectric constants (a table of values for typical materials is provided in the next section). Once the battery becomes disconnected, there is no path for a charge to flow to the battery from the capacitor plates. Hence, the insertion of the dielectric has no effect on the charge on the plate, which remains at a value of [latex]{Q}_{0}[/latex]. Therefore, we find that the capacitance of the capacitor with a dielectric is

This equation tells us that the capacitance [latex]{C}_{0}[/latex] of an empty (vacuum) capacitor can be increased by a factor of [latex]\kappa[/latex] when we insert a dielectric material to completely fill the space between its plates. Note that Equation 8.11 can also be used for an empty capacitor by setting [latex]\kappa =1[/latex]. In other words, we can say that the dielectric constant of the vacuum is 1, which is a reference value.

The principle expressed by Equation 8.11 is widely used in the construction industry (Figure 8.18). Metal plates in an electronic stud finder act effectively as a capacitor. You place a stud finder with its flat side on the wall and move it continually in the horizontal direction. When the finder moves over a wooden stud, the capacitance of its plates changes, because wood has a different dielectric constant than a gypsum wall. This change triggers a signal in a circuit, and thus the stud is detected.

The electrical energy stored by a capacitor is also affected by the presence of a dielectric. When the energy stored in an empty capacitor is [latex]{U}_{0}[/latex], the energy U stored in a capacitor with a dielectric is smaller by a factor of [latex]\kappa[/latex],

As a dielectric material sample is brought near an empty charged capacitor, the sample reacts to the electrical field of the charges on the capacitor plates. Just as we learned in Electric Charges and Fields on electrostatics, there will be the induced charges on the surface of the sample; however, they are not free charges like in a conductor, because a perfect insulator does not have freely moving charges. These induced charges on the dielectric surface are of an opposite sign to the free charges on the plates of the capacitor, and so they are attracted by the free charges on the plates. Consequently, the dielectric is “pulled” into the gap, and the work to polarize the dielectric material between the plates is done at the expense of the stored electrical energy, which is reduced, in accordance with Equation 8.12.