Chapter 4. The Second Law of Thermodynamics
4.2 Heat Engines
Learning Objectives
By the end of this section, you will be able to:
- Describe the function and components of a heat engine
- Explain the efficiency of an engine
- Calculate the efficiency of an engine for a given cycle of an ideal gas
A heat engine is a device used to extract heat from a source and then convert it into mechanical work that is used for all sorts of applications. For example, a steam engine on an old-style train can produce the work needed for driving the train. Several questions emerge from the construction and application of heat engines. For example, what is the maximum percentage of the heat extracted that can be used to do work? This turns out to be a question that can only be answered through the second law of thermodynamics.
The second law of thermodynamics can be formally stated in several ways. One statement presented so far is about the direction of spontaneous heat flow, known as the Clausius statement. A couple of other statements are based on heat engines. Whenever we consider heat engines and associated devices such as refrigerators and heat pumps, we do not use the normal sign convention for heat and work. For convenience, we assume that the symbols [latex]{Q}_{\text{h}},{Q}_{\text{c}},[/latex] and W represent only the amounts of heat transferred and work delivered, regardless what the givers or receivers are. Whether heat is entering or leaving a system and work is done to or by a system are indicated by proper signs in front of the symbols and by the directions of arrows in diagrams.
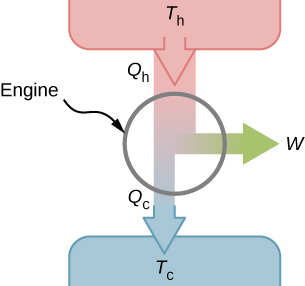
It turns out that we need more than one heat source/sink to construct a heat engine. We will come back to this point later in the chapter, when we compare different statements of the second law of thermodynamics. For the moment, we assume that a heat engine is constructed between a heat source (high-temperature reservoir or hot reservoir) and a heat sink (low-temperature reservoir or cold reservoir), represented schematically in Figure 4.4. The engine absorbs heat [latex]{Q}_{\text{h}}[/latex] from a heat source (hot reservoir) of Kelvin temperature [latex]{T}_{\text{h}},[/latex] uses some of that energy to produce useful work W, and then discards the remaining energy as heat [latex]{Q}_{\text{c}}[/latex] into a heat sink (cold reservoir) of Kelvin temperature [latex]{T}_{\text{c}}.[/latex] Power plants and internal combustion engines are examples of heat engines. Power plants use steam produced at high temperature to drive electric generators, while exhausting heat to the atmosphere or a nearby body of water in the role of the heat sink. In an internal combustion engine, a hot gas-air mixture is used to push a piston, and heat is exhausted to the nearby atmosphere in a similar manner.
Actual heat engines have many different designs. Examples include internal combustion engines, such as those used in most cars today, and external combustion engines, such as the steam engines used in old steam-engine trains. Figure 4.5 shows a photo of a nuclear power plant in operation. The atmosphere around the reactors acts as the cold reservoir, and the heat generated from the nuclear reaction provides the heat from the hot reservoir.

Heat engines operate by carrying a working substance through a cycle. In a steam power plant, the working substance is water, which starts as a liquid, becomes vaporized, is then used to drive a turbine, and is finally condensed back into the liquid state. As is the case for all working substances in cyclic processes, once the water returns to its initial state, it repeats the same sequence.
For now, we assume that the cycles of heat engines are reversible, so there is no energy loss to friction or other irreversible effects. Suppose that the engine of Figure 4.4 goes through one complete cycle and that [latex]{Q}_{\text{h}},{Q}_{\text{c}},[/latex] and W represent the heats exchanged and the work done for that cycle. Since the initial and final states of the system are the same, [latex]\text{Δ}{E}_{\text{int}}=0[/latex] for the cycle. We therefore have from the first law of thermodynamics,
so that
The most important measure of a heat engine is its efficiency (e), which is simply “what we get out” divided by “what we put in” during each cycle, as defined by [latex]e={W}_{\text{out}}\text{/}{Q}_{\text{in}}.[/latex]
With a heat engine working between two heat reservoirs, we get out W and put in [latex]{Q}_{\text{h}},[/latex] so the efficiency of the engine is
Here, we used Equation 4.1, [latex]W={Q}_{\text{h}}-{Q}_{\text{c}},[/latex] in the final step of this expression for the efficiency.
Example
A Lawn Mower
A lawn mower is rated to have an efficiency of [latex]25.0\text{%}[/latex] and an average power of 3.00 kW. What are (a) the average work and (b) the minimum heat discharge into the air by the lawn mower in one minute of use?
Strategy
From the average power—that is, the rate of work production—we can figure out the work done in the given elapsed time. Then, from the efficiency given, we can figure out the minimum heat discharge [latex]{Q}_{\text{c}}={Q}_{\text{h}}\left(1-e\right)[/latex] with [latex]{Q}_{\text{h}}={Q}_{\text{c}}+W.[/latex]
Solution
Show Answer
- The average work delivered by the lawn mower is
- The minimum heat discharged into the air is given by
which leads to
Significance
As the efficiency rises, the minimum heat discharged falls. This helps our environment and atmosphere by not having as much waste heat expelled.
Summary
- The work done by a heat engine is the difference between the heat absorbed from the hot reservoir and the heat discharged to the cold reservoir, that is, [latex]W={Q}_{\text{h}}-{Q}_{\text{c}}.[/latex]
- The ratio of the work done by the engine and the heat absorbed from the hot reservoir provides the efficiency of the engine, that is, [latex]e=W\text{/}{Q}_{\text{h}}=1-{Q}_{\text{c}}\text{/}{Q}_{\text{h}}.[/latex]
Conceptual Questions
Explain in practical terms why efficiency is defined as [latex]W\text{/}{Q}_{\text{h}}.[/latex]
Problems
An engine is found to have an efficiency of 0.40. If it does 200 J of work per cycle, what are the corresponding quantities of heat absorbed and discharged?
In performing 100.0 J of work, an engine discharges 50.0 J of heat. What is the efficiency of the engine?
Show Solution
0.667
An engine with an efficiency of 0.30 absorbs 500 J of heat per cycle. (a) How much work does it perform per cycle? (b) How much heat does it discharge per cycle?
It is found that an engine discharges 100.0 J while absorbing 125.0 J each cycle of operation. (a) What is the efficiency of the engine? (b) How much work does it perform per cycle?
Show Solution
a. 0.556; b. 125.0 J
The temperature of the cold reservoir of the engine is 300 K. It has an efficiency of 0.30 and absorbs 500 J of heat per cycle. (a) How much work does it perform per cycle? (b) How much heat does it discharge per cycle?
An engine absorbs three times as much heat as it discharges. The work done by the engine per cycle is 50 J. Calculate (a) the efficiency of the engine, (b) the heat absorbed per cycle, and (c) the heat discharged per cycle.
Show Solution
a. 0.50; b. 100 J; c. 50 J
A coal power plant consumes 100,000 kg of coal per hour and produces 500 MW of power. If the heat of combustion of coal is 30 MJ/kg, what is the efficiency of the power plant?
Glossary
- cold reservoir
- sink of heat used by a heat engine
- efficiency (e)
- output work from the engine over the input heat to the engine from the hot reservoir
- heat engine
- device that converts heat into work
- hot reservoir
- source of heat used by a heat engine
Licenses and Attributions
Heat Engines. Authored by: OpenStax College. Located at: https://openstax.org/books/university-physics-volume-2/pages/4-2-heat-engines. License: CC BY: Attribution. License Terms: Download for free at https://openstax.org/books/university-physics-volume-2/pages/1-introduction

