Chapter 3. The First Law of Thermodynamics
3.5 Heat Capacities of an Ideal Gas
Learning Objectives
By the end of this section, you will be able to:
- Define heat capacity of an ideal gas for a specific process
- Calculate the specific heat of an ideal gas for either an isobaric or isochoric process
- Explain the difference between the heat capacities of an ideal gas and a real gas
- Estimate the change in specific heat of a gas over temperature ranges
We learned about specific heat and molar heat capacity in Temperature and Heat; however, we have not considered a process in which heat is added. We do that in this section. First, we examine a process where the system has a constant volume, then contrast it with a system at constant pressure and show how their specific heats are related.
Let’s start with looking at Figure 3.12, which shows two vessels A and B, each containing 1 mol of the same type of ideal gas at a temperature T and a volume V. The only difference between the two vessels is that the piston at the top of A is fixed, whereas the one at the top of B is free to move against a constant external pressure p. We now consider what happens when the temperature of the gas in each vessel is slowly increased to [latex]T+dT[/latex] with the addition of heat.
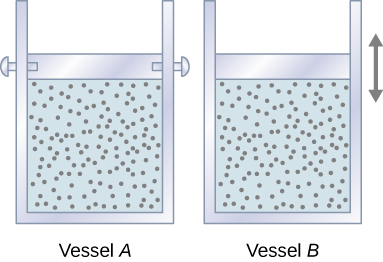
Since the piston of vessel A is fixed, the volume of the enclosed gas does not change. Consequently, the gas does no work, and we have from the first law
We represent the fact that the heat is exchanged at constant volume by writing
where [latex]{C}_{V}[/latex] is the molar heat capacity at constant volume of the gas. In addition, since [latex]d{E}_{\text{int}}=dQ[/latex] for this particular process,
We obtained this equation assuming the volume of the gas was fixed. However, internal energy is a state function that depends on only the temperature of an ideal gas. Therefore, [latex]d{E}_{\text{int}}={C}_{V}dT[/latex] gives the change in internal energy of an ideal gas for any process involving a temperature change dT.
When the gas in vessel B is heated, it expands against the movable piston and does work [latex]dW=pdV.[/latex] In this case, the heat is added at constant pressure, and we write
where [latex]{C}_{p}[/latex] is the molar heat capacity at constant pressure of the gas. Furthermore, since the ideal gas expands against a constant pressure,
becomes
Finally, inserting the expressions for dQ and pdV into the first law, we obtain
We have found [latex]d{E}_{\text{int}}[/latex] for both an isochoric and an isobaric process. Because the internal energy of an ideal gas depends only on the temperature, [latex]d{E}_{\text{int}}[/latex] must be the same for both processes. Thus,
and
The derivation of Equation 3.10 was based only on the ideal gas law. Consequently, this relationship is approximately valid for all dilute gases, whether monatomic like He, diatomic like [latex]{\text{O}}_{2},[/latex] or polyatomic like [latex]{\text{CO}}_{2}{\phantom{\rule{0.2em}{0ex}}\text{or NH}}_{3}\text{.}[/latex]
In the preceding chapter, we found the molar heat capacity of an ideal gas under constant volume to be
where d is the number of degrees of freedom of a molecule in the system. Table 3.3 shows the molar heat capacities of some dilute ideal gases at room temperature. The heat capacities of real gases are somewhat higher than those predicted by the expressions of [latex]{C}_{V}[/latex] and [latex]{C}_{p}[/latex] given in Equation 3.10. This indicates that vibrational motion in polyatomic molecules is significant, even at room temperature. Nevertheless, the difference in the molar heat capacities, [latex]{C}_{p}-{C}_{V},[/latex] is very close to R, even for the polyatomic gases.
| Molar Heat Capacities of Dilute Ideal Gases at Room Temperature | ||||
|---|---|---|---|---|
| Type of Molecule | Gas | [latex]{C}_{p}[/latex] (J/mol K) |
[latex]{C}_{V}[/latex] (J/mol K) |
[latex]{C}_{p}-{C}_{V}[/latex] (J/mol K) |
| Monatomic | Ideal | [latex]\frac{5}{2}R=20.79[/latex] | [latex]\frac{3}{2}R=12.47[/latex] | [latex]R=8.31[/latex] |
| Diatomic | Ideal | [latex]\frac{7}{2}R=29.10[/latex] | [latex]\frac{5}{2}R=20.79[/latex] | [latex]R=8.31[/latex] |
| Polyatomic | Ideal | [latex]4R=33.26[/latex] | [latex]3R=24.94[/latex] | [latex]R=8.31[/latex] |
Summary
- For an ideal gas, the molar capacity at constant pressure [latex]{C}_{p}[/latex] is given by [latex]{C}_{p}={C}_{V}+R=dR\text{/}2+R[/latex], where d is the number of degrees of freedom of each molecule/entity in the system.
- A real gas has a specific heat close to but a little bit higher than that of the corresponding ideal gas with [latex]{C}_{p}\simeq {C}_{V}+R.[/latex]
Conceptual Questions
How can an object transfer heat if the object does not possess a discrete quantity of heat?
Most materials expand when heated. One notable exception is water between [latex]0\phantom{\rule{0.2em}{0ex}}\text{°}\text{C}[/latex] and [latex]4\phantom{\rule{0.2em}{0ex}}\text{°}\text{C,}[/latex] which actually decreases in volume with the increase in temperature. Which is greater for water in this temperature region, [latex]{C}_{p}[/latex] or [latex]{C}_{V}[/latex] ?
Show Solution
Typically [latex]{C}_{p}[/latex] is greater than [latex]{C}_{V}[/latex] because when expansion occurs under constant pressure, it does work on the surroundings. Therefore, heat can go into internal energy and work. Under constant volume, all heat goes into internal energy. In this example, water contracts upon heating, so if we add heat at constant pressure, work is done on the water by surroundings and therefore, [latex]{C}_{p}[/latex] is less than [latex]{C}_{V}[/latex].
Why are there two specific heats for gases [latex]{C}_{p}[/latex] and [latex]{C}_{V}[/latex], yet only one given for solid?
Problems
The temperature of an ideal monatomic gas rises by 8.0 K. What is the change in the internal energy of 1 mol of the gas at constant volume?
Show Solution
100 J
For a temperature increase of [latex]10\phantom{\rule{0.2em}{0ex}}\text{°}\text{C}[/latex] at constant volume, what is the heat absorbed by (a) 3.0 mol of a dilute monatomic gas; (b) 0.50 mol of a dilute diatomic gas; and (c) 15 mol of a dilute polyatomic gas?
If the gases of the preceding problem are initially at 300 K, what are their internal energies after they absorb the heat?
Show Solution
a. 370 J; b. 100 J; c. 500 J
Consider 0.40 mol of dilute carbon dioxide at a pressure of 0.50 atm and a volume of 50 L. What is the internal energy of the gas?
When 400 J of heat are slowly added to 10 mol of an ideal monatomic gas, its temperature rises by [latex]10\phantom{\rule{0.2em}{0ex}}\text{°}\text{C}[/latex]. What is the work done on the gas?
Show Solution
850 J
One mole of a dilute diatomic gas occupying a volume of 10.00 L expands against a constant pressure of 2.000 atm when it is slowly heated. If the temperature of the gas rises by 10.00 K and 400.0 J of heat are added in the process, what is its final volume?
Glossary
- molar heat capacity at constant pressure
- quantifies the ratio of the amount of heat added removed to the temperature while measuring at constant pressure
- molar heat capacity at constant volume
- quantifies the ratio of the amount of heat added removed to the temperature while measuring at constant volume
Licenses and Attributions
Heat Capacities of an Ideal Gas. Authored by: OpenStax College. Located at: https://openstax.org/books/university-physics-volume-2/pages/3-5-heat-capacities-of-an-ideal-gas. License: CC BY: Attribution. License Terms: Download for free at https://openstax.org/books/university-physics-volume-2/pages/1-introduction

