Chapter 1. Temperature and Heat
1.6 Mechanisms of Heat Transfer
Learning Objectives
By the end of this section, you will be able to:
- Explain some phenomena that involve conductive, convective, and radiative heat transfer
- Solve problems on the relationships between heat transfer, time, and rate of heat transfer
- Solve problems using the formulas for conduction and radiation
Just as interesting as the effects of heat transfer on a system are the methods by which it occurs. Whenever there is a temperature difference, heat transfer occurs. It may occur rapidly, as through a cooking pan, or slowly, as through the walls of a picnic ice chest. So many processes involve heat transfer that it is hard to imagine a situation where no heat transfer occurs. Yet every heat transfer takes place by only three methods:
- Conduction is heat transfer through stationary matter by physical contact. (The matter is stationary on a macroscopic scale—we know that thermal motion of the atoms and molecules occurs at any temperature above absolute zero.) Heat transferred from the burner of a stove through the bottom of a pan to food in the pan is transferred by conduction.
- Convection is the heat transfer by the macroscopic movement of a fluid. This type of transfer takes place in a forced-air furnace and in weather systems, for example.
- Heat transfer by radiation occurs when microwaves, infrared radiation, visible light, or another form of electromagnetic radiation is emitted or absorbed. An obvious example is the warming of Earth by the Sun. A less obvious example is thermal radiation from the human body.
In the illustration at the beginning of this chapter, the fire warms the snowshoers’ faces largely by radiation. Convection carries some heat to them, but most of the air flow from the fire is upward (creating the familiar shape of flames), carrying heat to the food being cooked and into the sky. The snowshoers wear clothes designed with low conductivity to prevent heat flow out of their bodies.
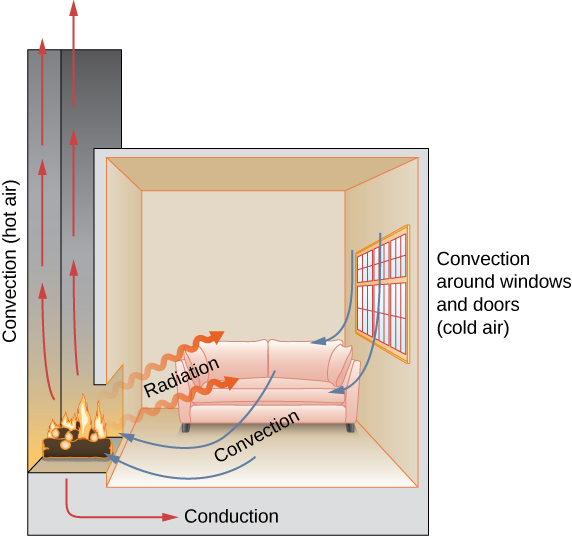
In this section, we examine these methods in some detail. Each method has unique and interesting characteristics, but all three have two things in common: They transfer heat solely because of a temperature difference, and the greater the temperature difference, the faster the heat transfer (Figure 1.19).
Check Your Understanding
Name an example from daily life (different from the text) for each mechanism of heat transfer.
Show Solution
Conduction: Heat transfers into your hands as you hold a hot cup of coffee. Convection: Heat transfers as the barista “steams” cold milk to make hot cocoa. Radiation: Heat transfers from the Sun to a jar of water with tea leaves in it to make “Sun tea.” A great many other answers are possible.
Conduction
As you walk barefoot across the living room carpet in a cold house and then step onto the kitchen tile floor, your feet feel colder on the tile. This result is intriguing, since the carpet and tile floor are both at the same temperature. The different sensation is explained by the different rates of heat transfer: The heat loss is faster for skin in contact with the tiles than with the carpet, so the sensation of cold is more intense.
Some materials conduct thermal energy faster than others. Figure 1.20 shows a material that conducts heat slowly—it is a good thermal insulator, or poor heat conductor—used to reduce heat flow into and out of a house.

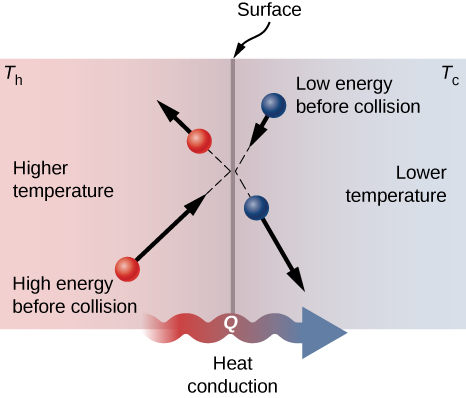
A molecular picture of heat conduction will help justify the equation that describes it. Figure 1.21 shows molecules in two bodies at different temperatures, [latex]{T}_{\text{h}}[/latex] and [latex]{T}_{\text{c}},[/latex] for “hot” and “cold.” The average kinetic energy of a molecule in the hot body is higher than in the colder body. If two molecules collide, energy transfers from the high-energy to the low-energy molecule. In a metal, the picture would also include free valence electrons colliding with each other and with atoms, likewise transferring energy. The cumulative effect of all collisions is a net flux of heat from the hotter body to the colder body. Thus, the rate of heat transfer increases with increasing temperature difference [latex]\text{Δ}T={T}_{\text{h}}-{T}_{\text{c}}.[/latex] If the temperatures are the same, the net heat transfer rate is zero. Because the number of collisions increases with increasing area, heat conduction is proportional to the cross-sectional area—a second factor in the equation.
A third quantity that affects the conduction rate is the thickness of the material through which heat transfers. Figure 1.22 shows a slab of material with a higher temperature on the left than on the right. Heat transfers from the left to the right by a series of molecular collisions. The greater the distance between hot and cold, the more time the material takes to transfer the same amount of heat.
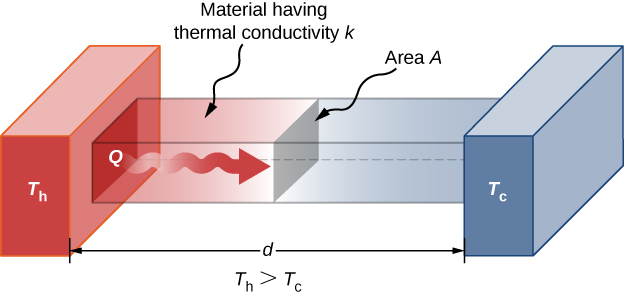
All four of these quantities appear in a simple equation deduced from and confirmed by experiments. The rate of conductive heat transfer through a slab of material, such as the one in Figure 1.22, is given by
where P is the power or rate of heat transfer in watts or in kilocalories per second, A and d are its surface area and thickness, as shown in Figure 1.22, [latex]{T}_{\text{h}}-{T}_{\text{c}}[/latex] is the temperature difference across the slab, and k is the thermal conductivity of the material. Table 1.5 gives representative values of thermal conductivity.
More generally, we can write
where x is the coordinate in the direction of heat flow. Since in Figure 1.22, the power and area are constant, dT/dx is constant, and the temperature decreases linearly from [latex]{T}_{\text{h}}[/latex] to [latex]{T}_{\text{c}}.[/latex]
| Substance | Thermal Conductivity k [latex]\left(\text{W}\text{/}\text{m}·\text{°C}\right)[/latex] |
|---|---|
| Diamond | 2000 |
| Silver | 420 |
| Copper | 390 |
| Gold | 318 |
| Aluminum | 220 |
| Steel iron | 80 |
| Steel (stainless) | 14 |
| Ice | 2.2 |
| Glass (average) | 0.84 |
| Concrete brick | 0.84 |
| Water | 0.6 |
| Fatty tissue (without blood) | 0.2 |
| Asbestos | 0.16 |
| Plasterboard | 0.16 |
| Wood | 0.08–0.16 |
| Snow (dry) | 0.10 |
| Cork | 0.042 |
| Glass wool | 0.042 |
| Wool | 0.04 |
| Down feathers | 0.025 |
| Air | 0.023 |
| Polystyrene foam | 0.010 |
Example
Calculating Heat Transfer through Conduction
A polystyrene foam icebox has a total area of [latex]0.950\phantom{\rule{0.2em}{0ex}}{\text{m}}^{2}[/latex] and walls with an average thickness of 2.50 cm. The box contains ice, water, and canned beverages at [latex]0\phantom{\rule{0.2em}{0ex}}\text{°}\text{C}\text{.}[/latex] The inside of the box is kept cold by melting ice. How much ice melts in one day if the icebox is kept in the trunk of a car at [latex]35.0\phantom{\rule{0.2em}{0ex}}\text{ºC}[/latex]?
Strategy
This question involves both heat for a phase change (melting of ice) and the transfer of heat by conduction. To find the amount of ice melted, we must find the net heat transferred. This value can be obtained by calculating the rate of heat transfer by conduction and multiplying by time.
Solution
Show Answer
First we identify the knowns.
[latex]k=0.010\phantom{\rule{0.2em}{0ex}}\text{W/m}·\text{°}\text{C}[/latex] for polystyrene foam; [latex]A=0.950\phantom{\rule{0.2em}{0ex}}{\text{m}}^{2};[/latex] [latex]d=2.50\phantom{\rule{0.2em}{0ex}}\text{cm}=0.0250\phantom{\rule{0.2em}{0ex}}\text{m;}[/latex];[latex]{T}_{\text{c}}=0\phantom{\rule{0.2em}{0ex}}\text{°}\text{C;}[/latex] [latex]{T}_{\text{h}}=35.0\phantom{\rule{0.2em}{0ex}}\text{°}\text{C}[/latex]; [latex]t=1\phantom{\rule{0.2em}{0ex}}\text{day}=24\phantom{\rule{0.2em}{0ex}}\text{hours}\phantom{\rule{0.2em}{0ex}}\text{-}\phantom{\rule{0.2em}{0ex}}86,400\phantom{\rule{0.2em}{0ex}}\text{s.}[/latex]
Then we identify the unknowns. We need to solve for the mass of the ice, m. We also need to solve for the net heat transferred to melt the ice, Q. The rate of heat transfer by conduction is given by
The heat used to melt the ice is [latex]Q=m{L}_{\text{f}}[/latex].We insert the known values:
Multiplying the rate of heat transfer by the time we obtain
We set this equal to the heat transferred to melt the ice, [latex]Q=m{L}_{\text{f}},[/latex] and solve for the mass m:
Significance
The result of 3.44 kg, or about 7.6 lb, seems about right, based on experience. You might expect to use about a 4 kg (7–10 lb) bag of ice per day. A little extra ice is required if you add any warm food or beverages.
Table 1.5 shows that polystyrene foam is a very poor conductor and thus a good insulator. Other good insulators include fiberglass, wool, and goosedown feathers. Like polystyrene foam, these all contain many small pockets of air, taking advantage of air’s poor thermal conductivity.
In developing insulation, the smaller the conductivity k and the larger the thickness d, the better. Thus, the ratio d/k, called the R factor, is large for a good insulator. The rate of conductive heat transfer is inversely proportional to R. R factors are most commonly quoted for household insulation, refrigerators, and the like. Unfortunately, in the United States, R is still in non-metric units of [latex]{\text{ft}}^{2}·\text{°F}·\text{h/Btu}[/latex], although the unit usually goes unstated [1 British thermal unit (Btu) is the amount of energy needed to change the temperature of 1.0 lb of water by [latex]1.0\phantom{\rule{0.2em}{0ex}}\text{°}\text{F}[/latex], which is 1055.1 J]. A couple of representative values are an R factor of 11 for 3.5-inch-thick fiberglass batts (pieces) of insulation and an R factor of 19 for 6.5-inch-thick fiberglass batts (Figure 1.23). In the US, walls are usually insulated with 3.5-inch batts, whereas ceilings are usually insulated with 6.5-inch batts. In cold climates, thicker batts may be used.

Note that in Table 1.5, most of the best thermal conductors—silver, copper, gold, and aluminum—are also the best electrical conductors, because they contain many free electrons that can transport thermal energy. (Diamond, an electrical insulator, conducts heat by atomic vibrations.) Cooking utensils are typically made from good conductors, but the handles of those used on the stove are made from good insulators (bad conductors).
Example
Two Conductors End to End
A steel rod and an aluminum rod, each of diameter 1.00 cm and length 25.0 cm, are welded end to end. One end of the steel rod is placed in a large tank of boiling water at [latex]100\phantom{\rule{0.2em}{0ex}}\text{°}\text{C}[/latex], while the far end of the aluminum rod is placed in a large tank of water at [latex]20\phantom{\rule{0.2em}{0ex}}\text{°}\text{C}[/latex]. The rods are insulated so that no heat escapes from their surfaces. What is the temperature at the joint, and what is the rate of heat conduction through this composite rod?
Strategy
The heat that enters the steel rod from the boiling water has no place to go but through the steel rod, then through the aluminum rod, to the cold water. Therefore, we can equate the rate of conduction through the steel to the rate of conduction through the aluminum.
We repeat the calculation with a second method, in which we use the thermal resistance R of the rod, since it simply adds when two rods are joined end to end. (We will use a similar method in the chapter on direct-current circuits.)
Solution
Show Answer
- Identify the knowns and convert them to SI units.
The length of each rod is [latex]{L}_{\text{A1}}={L}_{\text{steel}}=0.25\phantom{\rule{0.2em}{0ex}}\text{m,}[/latex] the cross-sectional area of each rod is [latex]{A}_{\text{A1}}={A}_{\text{steel}}=7.85\phantom{\rule{0.2em}{0ex}}×\phantom{\rule{0.2em}{0ex}}{10}^{-5}\phantom{\rule{0.2em}{0ex}}{\text{m}}^{2}\text{,}[/latex] the thermal conductivity of aluminum is [latex]{k}_{\text{A1}}=220\phantom{\rule{0.2em}{0ex}}\text{W/m}·\text{°}\text{C}[/latex], the thermal conductivity of steel is [latex]{k}_{\text{steel}}=80\phantom{\rule{0.2em}{0ex}}\text{W/m}·\text{°}\text{C}[/latex], the temperature at the hot end is [latex]T=100\phantom{\rule{0.2em}{0ex}}\text{°}\text{C}[/latex], and the temperature at the cold end is [latex]T=20\phantom{\rule{0.2em}{0ex}}\text{°}\text{C}[/latex]. - Calculate the heat-conduction rate through the steel rod and the heat-conduction rate through the aluminum rod in terms of the unknown temperature T at the joint:
- Set the two rates equal and solve for the unknown temperature:
- Calculate either rate:
- If desired, check your answer by calculating the other rate.
Solution
Show Answer
- Recall that [latex]R=L\text{/}k[/latex]. Now [latex]P=A\text{Δ}T\text{/}R,\phantom{\rule{0.2em}{0ex}}\text{or}\phantom{\rule{0.2em}{0ex}}\text{Δ}T=PR\text{/}A.[/latex]
- We know that [latex]\text{Δ}{T}_{\text{steel}}+\text{Δ}{T}_{\text{Al}}=100\phantom{\rule{0.2em}{0ex}}\text{°}\text{C}-20\phantom{\rule{0.2em}{0ex}}\text{°}\text{C}=80\phantom{\rule{0.2em}{0ex}}\text{°}\text{C}[/latex]. We also know that [latex]{P}_{\text{steel}}={P}_{\text{Al}},[/latex] and we denote that rate of heat flow by P. Combine the equations:
Thus, we can simply add R factors. Now, [latex]P=\frac{80\phantom{\rule{0.2em}{0ex}}\text{°}\text{C}}{A\left({R}_{\text{steel}}+{R}_{\text{Al}}\right)}[/latex].
- Find the [latex]{R}_{s}[/latex] from the known quantities:
and
- Substitute these values in to find [latex]P=1.47\phantom{\rule{0.2em}{0ex}}\text{W}[/latex] as before.
- Determine [latex]\text{Δ}T[/latex] for the aluminum rod (or for the steel rod) and use it to find T at the joint.
[latex]\text{Δ}{T}_{\text{Al}}=\frac{P{R}_{\text{Al}}}{A}=\frac{\left(1.47\phantom{\rule{0.2em}{0ex}}\text{W}\right)\left(1.14\phantom{\rule{0.2em}{0ex}}×\phantom{\rule{0.2em}{0ex}}{10}^{-3}\phantom{\rule{0.2em}{0ex}}{\text{m}}^{2}·\text{°}\text{C/W}\right)}{7.85\phantom{\rule{0.2em}{0ex}}×\phantom{\rule{0.2em}{0ex}}{10}^{-5}\phantom{\rule{0.2em}{0ex}}{\text{m}}^{2}}=21.3\phantom{\rule{0.2em}{0ex}}\text{°}\text{C,}[/latex]
so [latex]T=20\phantom{\rule{0.2em}{0ex}}\text{°}\text{C}+21.3\phantom{\rule{0.2em}{0ex}}\text{°}\text{C}=41.3\phantom{\rule{0.2em}{0ex}}\text{°}\text{C}[/latex], as in Solution [latex]1[/latex]. - If desired, check by determining [latex]\text{Δ}T[/latex] for the other rod.
Significance
In practice, adding R values is common, as in calculating the R value of an insulated wall. In the analogous situation in electronics, the resistance corresponds to AR in this problem and is additive even when the areas are unequal, as is common in electronics. Our equation for heat conduction can be used only when the areas are equal; otherwise, we would have a problem in three-dimensional heat flow, which is beyond our scope.
Check Your Understanding
How does the rate of heat transfer by conduction change when all spatial dimensions are doubled?
Show Solution
Because area is the product of two spatial dimensions, it increases by a factor of four when each dimension is doubled [latex]\left({A}_{\text{final}}={\left(2d\right)}^{2}=4{d}^{2}=4{A}_{\text{initial}}\right)[/latex]. The distance, however, simply doubles. Because the temperature difference and the coefficient of thermal conductivity are independent of the spatial dimensions, the rate of heat transfer by conduction increases by a factor of four divided by two, or two:
[latex]{P}_{\text{final}}=\frac{k{A}_{\text{final}}\left({T}_{\text{h}}-{T}_{\text{c}}\right)}{{d}_{\text{final}}}=\frac{k\left(4{A}_{\text{final}}\left({T}_{\text{h}}-{T}_{\text{c}}\right)\right)}{2{d}_{\text{initial}}}=2\frac{k{A}_{\text{final}}\left({T}_{\text{h}}-{T}_{\text{c}}\right)}{{d}_{\text{initial}}}=2{P}_{\text{initial}}[/latex].
Conduction is caused by the random motion of atoms and molecules. As such, it is an ineffective mechanism for heat transport over macroscopic distances and short times. For example, the temperature on Earth would be unbearably cold during the night and extremely hot during the day if heat transport in the atmosphere were only through conduction. Also, car engines would overheat unless there was a more efficient way to remove excess heat from the pistons. The next module discusses the important heat-transfer mechanism in such situations.
Convection
In convection, thermal energy is carried by the large-scale flow of matter. It can be divided into two types. In forced convection, the flow is driven by fans, pumps, and the like. A simple example is a fan that blows air past you in hot surroundings and cools you by replacing the air heated by your body with cooler air. A more complicated example is the cooling system of a typical car, in which a pump moves coolant through the radiator and engine to cool the engine and a fan blows air to cool the radiator.
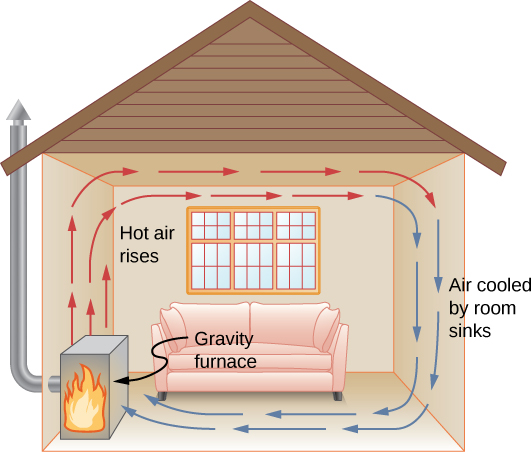
In free or natural convection, the flow is driven by buoyant forces: hot fluid rises and cold fluid sinks because density decreases as temperature increases. The house in Figure 1.24 is kept warm by natural convection, as is the pot of water on the stove in Figure 1.25. Ocean currents and large-scale atmospheric circulation, which result from the buoyancy of warm air and water, transfer hot air from the tropics toward the poles and cold air from the poles toward the tropics. (Earth’s rotation interacts with those flows, causing the observed eastward flow of air in the temperate zones.)
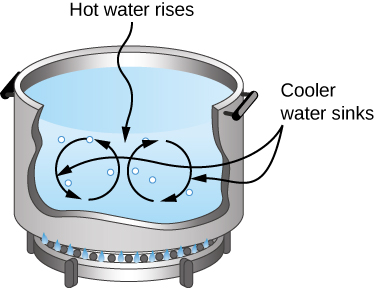
Natural convection like that of Figure 1.24 and Figure 1.25, but acting on rock in Earth’s mantle, drives plate tectonics that are the motions that have shaped Earth’s surface.
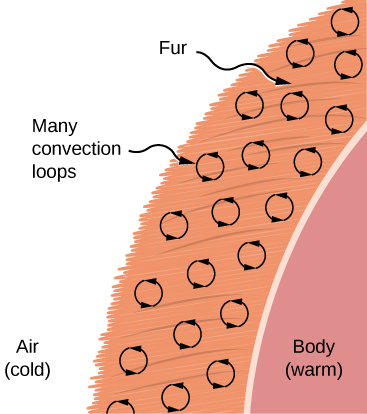
Convection is usually more complicated than conduction. Beyond noting that the convection rate is often approximately proportional to the temperature difference, we will not do any quantitative work comparable to the formula for conduction. However, we can describe convection qualitatively and relate convection rates to heat and time. Air is a poor conductor, so convection dominates heat transfer by air. Therefore, the amount of available space for airflow determines whether air transfers heat rapidly or slowly. There is little heat transfer in a space filled with air with a small amount of other material that prevents flow. The space between the inside and outside walls of a typical American house, for example, is about 9 cm (3.5 in.)—large enough for convection to work effectively. The addition of wall insulation prevents airflow, so heat loss (or gain) is decreased. On the other hand, the gap between the two panes of a double-paned window is about 1 cm, which largely prevents convection and takes advantage of air’s low conductivity reduce heat loss. Fur, cloth, and fiberglass also take advantage of the low conductivity of air by trapping it in spaces too small to support convection (Figure 1.26).
Some interesting phenomena happen when convection is accompanied by a phase change. The combination allows us to cool off by sweating even if the temperature of the surrounding air exceeds body temperature. Heat from the skin is required for sweat to evaporate from the skin, but without air flow, the air becomes saturated and evaporation stops. Air flow caused by convection replaces the saturated air by dry air and evaporation continues.
Example
Calculating the Flow of Mass during Convection
The average person produces heat at the rate of about 120 W when at rest. At what rate must water evaporate from the body to get rid of all this energy? (For simplicity, we assume this evaporation occurs when a person is sitting in the shade and surrounding temperatures are the same as skin temperature, eliminating heat transfer by other methods.)
Strategy
Energy is needed for this phase change ([latex]Q=m{L}_{v}[/latex]). Thus, the energy loss per unit time is
We divide both sides of the equation by [latex]{L}_{v}[/latex] to find that the mass evaporated per unit time is
Solution
Show Answer
Insert the value of the latent heat from Table 1.4, [latex]{L}_{v}=2430\phantom{\rule{0.2em}{0ex}}\text{kJ/kg}=2430\phantom{\rule{0.2em}{0ex}}\text{J/g}[/latex]. This yields
Significance
Evaporating about 3 g/min seems reasonable. This would be about 180 g (about 7 oz.) per hour. If the air is very dry, the sweat may evaporate without even being noticed. A significant amount of evaporation also takes place in the lungs and breathing passages.
Another important example of the combination of phase change and convection occurs when water evaporates from the oceans. Heat is removed from the ocean when water evaporates. If the water vapor condenses in liquid droplets as clouds form, possibly far from the ocean, heat is released in the atmosphere. Thus, there is an overall transfer of heat from the ocean to the atmosphere. This process is the driving power behind thunderheads, those great cumulus clouds that rise as much as 20.0 km into the stratosphere (Figure 1.27). Water vapor carried in by convection condenses, releasing tremendous amounts of energy. This energy causes the air to expand and rise to colder altitudes. More condensation occurs in these regions, which in turn drives the cloud even higher. This mechanism is an example of positive feedback, since the process reinforces and accelerates itself. It sometimes produces violent storms, with lightning and hail. The same mechanism drives hurricanes.
This time-lapse video shows convection currents in a thunderstorm, including “rolling” motion similar to that of boiling water.

Check Your Understanding
Explain why using a fan in the summer feels refreshing.
Show Solution
Using a fan increases the flow of air: Warm air near your body is replaced by cooler air from elsewhere. Convection increases the rate of heat transfer so that moving air “feels” cooler than still air.
Radiation
You can feel the heat transfer from the Sun. The space between Earth and the Sun is largely empty, so the Sun warms us without any possibility of heat transfer by convection or conduction. Similarly, you can sometimes tell that the oven is hot without touching its door or looking inside—it may just warm you as you walk by. In these examples, heat is transferred by radiation (Figure 1.28). That is, the hot body emits electromagnetic waves that are absorbed by the skin. No medium is required for electromagnetic waves to propagate. Different names are used for electromagnetic waves of different wavelengths: radio waves, microwaves, infrared radiation, visible light, ultraviolet radiation, X-rays, and gamma rays.

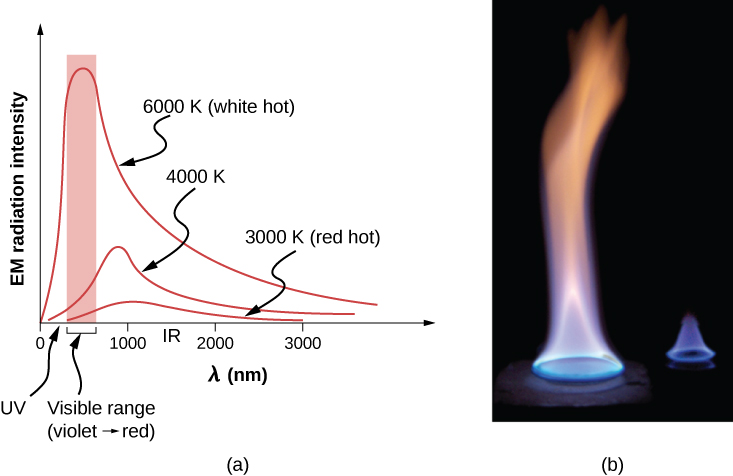
The energy of electromagnetic radiation varies over a wide range, depending on the wavelength: A shorter wavelength (or higher frequency) corresponds to a higher energy. Because more heat is radiated at higher temperatures, higher temperatures produce more intensity at every wavelength but especially at shorter wavelengths. In visible light, wavelength determines color—red has the longest wavelength and violet the shortest—so a temperature change is accompanied by a color change. For example, an electric heating element on a stove glows from red to orange, while the higher-temperature steel in a blast furnace glows from yellow to white. Infrared radiation is the predominant form radiated by objects cooler than the electric element and the steel. The radiated energy as a function of wavelength depends on its intensity, which is represented in Figure 1.29 by the height of the distribution. (Electromagnetic Waves explains more about the electromagnetic spectrum, and Photons and Matter Waves discusses why the decrease in wavelength corresponds to an increase in energy.)
The rate of heat transfer by radiation also depends on the object’s color. Black is the most effective, and white is the least effective. On a clear summer day, black asphalt in a parking lot is hotter than adjacent gray sidewalk, because black absorbs better than gray (Figure 1.30). The reverse is also true—black radiates better than gray. Thus, on a clear summer night, the asphalt is colder than the gray sidewalk, because black radiates the energy more rapidly than gray. A perfectly black object would be an ideal radiator and an ideal absorber, as it would capture all the radiation that falls on it. In contrast, a perfectly white object or a perfect mirror would reflect all radiation, and a perfectly transparent object would transmit it all (Figure 1.31). Such objects would not emit any radiation. Mathematically, the color is represented by the emissivity e. A “blackbody” radiator would have an [latex]e=1[/latex], whereas a perfect reflector or transmitter would have [latex]e=0[/latex]. For real examples, tungsten light bulb filaments have an e of about 0.5, and carbon black (a material used in printer toner) has an emissivity of about 0.95.

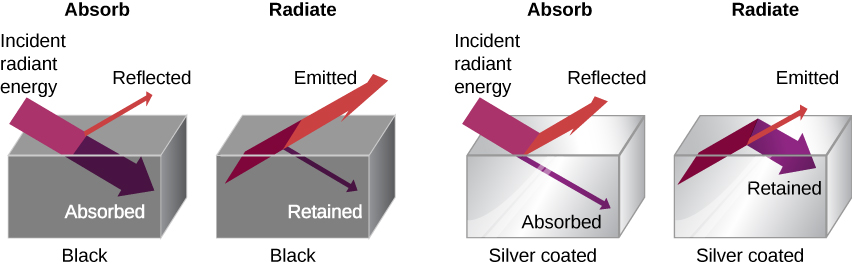
To see that, consider a silver object and a black object that can exchange heat by radiation and are in thermal equilibrium. We know from experience that they will stay in equilibrium (the result of a principle that will be discussed at length in Second Law of Thermodynamics). For the black object’s temperature to stay constant, it must emit as much radiation as it absorbs, so it must be as good at radiating as absorbing. Similar considerations show that the silver object must radiate as little as it absorbs. Thus, one property, emissivity, controls both radiation and absorption.
Finally, the radiated heat is proportional to the object’s surface area, since every part of the surface radiates. If you knock apart the coals of a fire, the radiation increases noticeably due to an increase in radiating surface area.
The rate of heat transfer by emitted radiation is described by the Stefan-Boltzmann law of radiation:
where [latex]\sigma =5.67\phantom{\rule{0.2em}{0ex}}×\phantom{\rule{0.2em}{0ex}}{10}^{-8}\phantom{\rule{0.2em}{0ex}}\text{J/s}·{\text{m}}^{2}·{\text{K}}^{4}[/latex] is the Stefan-Boltzmann constant, a combination of fundamental constants of nature; A is the surface area of the object; and T is its temperature in kelvins.
The proportionality to the fourth power of the absolute temperature is a remarkably strong temperature dependence. It allows the detection of even small temperature variations. Images called thermographs can be used medically to detect regions of abnormally high temperature in the body, perhaps indicative of disease. Similar techniques can be used to detect heat leaks in homes (Figure 1.32), optimize performance of blast furnaces, improve comfort levels in work environments, and even remotely map Earth’s temperature profile.

The Stefan-Boltzmann equation needs only slight refinement to deal with a simple case of an object’s absorption of radiation from its surroundings. Assuming that an object with a temperature [latex]{T}_{1}[/latex] is surrounded by an environment with uniform temperature [latex]{T}_{2}[/latex], the net rate of heat transfer by radiation is
where e is the emissivity of the object alone. In other words, it does not matter whether the surroundings are white, gray, or black: The balance of radiation into and out of the object depends on how well it emits and absorbs radiation. When [latex]{T}_{2}>{T}_{1},[/latex] the quantity [latex]{P}_{\text{net}}[/latex] is positive, that is, the net heat transfer is from hot to cold.
Before doing an example, we have a complication to discuss: different emissivities at different wavelengths. If the fraction of incident radiation an object reflects is the same at all visible wavelengths, the object is gray; if the fraction depends on the wavelength, the object has some other color. For instance, a red or reddish object reflects red light more strongly than other visible wavelengths. Because it absorbs less red, it radiates less red when hot. Differential reflection and absorption of wavelengths outside the visible range have no effect on what we see, but they may have physically important effects. Skin is a very good absorber and emitter of infrared radiation, having an emissivity of 0.97 in the infrared spectrum. Thus, in spite of the obvious variations in skin color, we are all nearly black in the infrared. This high infrared emissivity is why we can so easily feel radiation on our skin. It is also the basis for the effectiveness of night-vision scopes used by law enforcement and the military to detect human beings.
Example
Calculating the Net Heat Transfer of a Person
What is the rate of heat transfer by radiation of an unclothed person standing in a dark room whose ambient temperature is [latex]22.0\phantom{\rule{0.2em}{0ex}}\text{°}\text{C}[/latex]? The person has a normal skin temperature of [latex]33.0\phantom{\rule{0.2em}{0ex}}\text{°}\text{C}[/latex] and a surface area of [latex]1.50\phantom{\rule{0.2em}{0ex}}{\text{m}}^{2}.[/latex] The emissivity of skin is 0.97 in the infrared, the part of the spectrum where the radiation takes place.
Strategy
We can solve this by using the equation for the rate of radiative heat transfer.
Solution
Show Answer
Insert the temperature values [latex]{T}_{2}=295\phantom{\rule{0.2em}{0ex}}\text{K}[/latex] and [latex]{T}_{1}=306\phantom{\rule{0.2em}{0ex}}\text{K}[/latex], so that
Significance
This value is a significant rate of heat transfer to the environment (note the minus sign), considering that a person at rest may produce energy at the rate of 125 W and that conduction and convection are also transferring energy to the environment. Indeed, we would probably expect this person to feel cold. Clothing significantly reduces heat transfer to the environment by all mechanisms, because clothing slows down both conduction and convection, and has a lower emissivity (especially if it is light-colored) than skin.
The average temperature of Earth is the subject of much current discussion. Earth is in radiative contact with both the Sun and dark space, so we cannot use the equation for an environment at a uniform temperature. Earth receives almost all its energy from radiation of the Sun and reflects some of it back into outer space. Conversely, dark space is very cold, about 3 K, so that Earth radiates energy into the dark sky. The rate of heat transfer from soil and grasses can be so rapid that frost may occur on clear summer evenings, even in warm latitudes.
The average temperature of Earth is determined by its energy balance. To a first approximation, it is the temperature at which Earth radiates heat to space as fast as it receives energy from the Sun.
An important parameter in calculating the temperature of Earth is its emissivity (e). On average, it is about 0.65, but calculation of this value is complicated by the great day-to-day variation in the highly reflective cloud coverage. Because clouds have lower emissivity than either oceans or land masses, they reflect some of the radiation back to the surface, greatly reducing heat transfer into dark space, just as they greatly reduce heat transfer into the atmosphere during the day. There is negative feedback (in which a change produces an effect that opposes that change) between clouds and heat transfer; higher temperatures evaporate more water to form more clouds, which reflect more radiation back into space, reducing the temperature.
The often-mentioned greenhouse effect is directly related to the variation of Earth’s emissivity with wavelength (Figure 1.33). The greenhouse effect is a natural phenomenon responsible for providing temperatures suitable for life on Earth and for making Venus unsuitable for human life. Most of the infrared radiation emitted from Earth is absorbed by carbon dioxide ([latex]{\text{CO}}_{2}[/latex]) and water ([latex]{\text{H}}_{2}\text{O}[/latex]) in the atmosphere and then re-radiated into outer space or back to Earth. Re-radiation back to Earth maintains its surface temperature about [latex]40\phantom{\rule{0.2em}{0ex}}\text{°C}[/latex] higher than it would be if there were no atmosphere. (The glass walls and roof of a greenhouse increase the temperature inside by blocking convective heat losses, not radiative losses.)
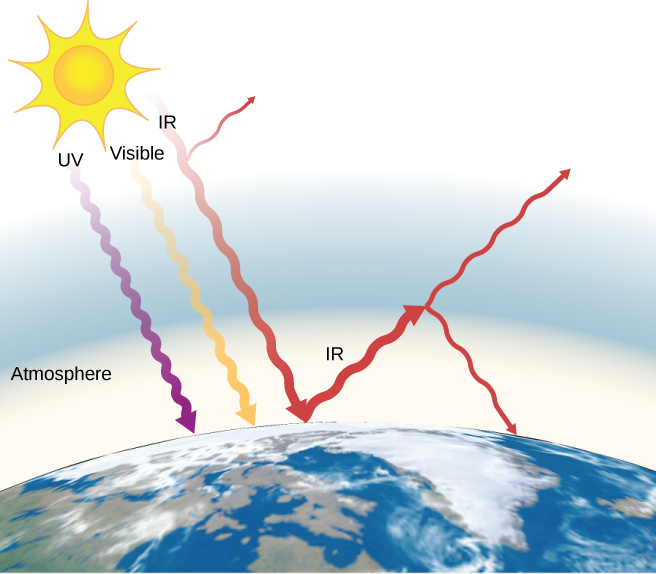
The greenhouse effect is central to the discussion of global warming due to emission of carbon dioxide and methane (and other greenhouse gases) into Earth’s atmosphere from industry, transportation, and farming. Changes in global climate could lead to more intense storms, precipitation changes (affecting agriculture), reduction in rain forest biodiversity, and rising sea levels.
You can explore a simulation of the greenhouse effect that takes the point of view that the atmosphere scatters (redirects) infrared radiation rather than absorbing it and reradiating it. You may want to run the simulation first with no greenhouse gases in the atmosphere and then look at how adding greenhouse gases affects the infrared radiation from the Earth and the Earth’s temperature.
Problem-Solving Strategy: Effects of Heat Transfer
- Examine the situation to determine what type of heat transfer is involved.
- Identify the type(s) of heat transfer—conduction, convection, or radiation.
- Identify exactly what needs to be determined in the problem (identify the unknowns). A written list is useful.
- Make a list of what is given or what can be inferred from the problem as stated (identify the knowns).
- Solve the appropriate equation for the quantity to be determined (the unknown).
- For conduction, use the equation [latex]P=\frac{kA\text{Δ}T}{d}[/latex]. Table 1.5 lists thermal conductivities. For convection, determine the amount of matter moved and the equation [latex]Q=mc\text{Δ}T[/latex], along with [latex]Q=m{L}_{\text{f}}[/latex] or [latex]Q=m{L}_{\text{V}}[/latex] if a substance changes phase. For radiation, the equation [latex]{P}_{\text{net}}=\sigma eA\left({T}_{2}{}^{4}-{T}_{1}{}^{4}\right)[/latex] gives the net heat transfer rate.
- Substitute the knowns along with their units into the appropriate equation and obtain numerical solutions complete with units.
- Check the answer to see if it is reasonable. Does it make sense?
Check Your Understanding
How much greater is the rate of heat radiation when a body is at the temperature [latex]40\phantom{\rule{0.2em}{0ex}}\text{°}\text{C}[/latex] than when it is at the temperature [latex]20\phantom{\rule{0.2em}{0ex}}\text{°}\text{C}[/latex]?
Show Solution
The radiated heat is proportional to the fourth power of the absolute temperature. Because [latex]{T}_{1}=293\phantom{\rule{0.2em}{0ex}}\text{K}[/latex] and [latex]{T}_{2}=313\phantom{\rule{0.2em}{0ex}}\text{K}[/latex], the rate of heat transfer increases by about 30% of the original rate.
Summary
- Heat is transferred by three different methods: conduction, convection, and radiation.
- Heat conduction is the transfer of heat between two objects in direct contact with each other.
- The rate of heat transfer P (energy per unit time) is proportional to the temperature difference [latex]{T}_{\text{h}}-{T}_{\text{c}}[/latex] and the contact area A and inversely proportional to the distance d between the objects.
- Convection is heat transfer by the macroscopic movement of mass. Convection can be natural or forced, and generally transfers thermal energy faster than conduction. Convection that occurs along with a phase change can transfer energy from cold regions to warm ones.
- Radiation is heat transfer through the emission or absorption of electromagnetic waves.
- The rate of radiative heat transfer is proportional to the emissivity e. For a perfect blackbody, [latex]e=1[/latex], whereas a perfectly white, clear, or reflective body has [latex]e=0[/latex], with real objects having values of e between 1 and 0.
- The rate of heat transfer depends on the surface area and the fourth power of the absolute temperature:
[latex]P=\sigma eA{T}^{4},[/latex]
where [latex]\sigma =5.67\phantom{\rule{0.2em}{0ex}}×\phantom{\rule{0.2em}{0ex}}{10}^{-8}\phantom{\rule{0.2em}{0ex}}\text{J/s}·{\text{m}}^{2}·{\text{K}}^{4}[/latex] is the Stefan-Boltzmann constant and e is the emissivity of the body. The net rate of heat transfer from an object by radiation is
[latex]\frac{{Q}_{\text{net}}}{t}=\sigma eA\left({T}_{2}{}^{4}-{T}_{1}{}^{4}\right),[/latex]
where [latex]{T}_{1}[/latex] is the temperature of the object surrounded by an environment with uniform temperature [latex]{T}_{2}[/latex] and e is the emissivity of the object.
Key Equations
| Linear thermal expansion | [latex]\text{Δ}L=\alpha L\text{Δ}T[/latex] |
| Thermal expansion in two dimensions | [latex]\text{Δ}A=2\alpha A\text{Δ}T[/latex] |
| Thermal expansion in three dimensions | [latex]\text{Δ}V=\beta V\text{Δ}T[/latex] |
| Heat transfer | [latex]Q=mc\text{Δ}T[/latex] |
| Transfer of heat in a calorimeter | [latex]{Q}_{\text{cold}}+{Q}_{\text{hot}}=0[/latex] |
| Heat due to phase change (melting and freezing) | [latex]Q=m{L}_{\text{f}}[/latex] |
| Heat due to phase change (evaporation and condensation) | [latex]Q=m{L}_{\text{v}}[/latex] |
| Rate of conductive heat transfer | [latex]P=\frac{kA\left({T}_{h}-{T}_{c}\right)}{d}[/latex] |
| Net rate of heat transfer by radiation | [latex]{P}_{\text{net}}=\sigma eA\left({T}_{2}{}^{4}-{T}_{1}{}^{4}\right)[/latex] |
Conceptual Questions
What are the main methods of heat transfer from the hot core of Earth to its surface? From Earth’s surface to outer space?
When our bodies get too warm, they respond by sweating and increasing blood circulation to the surface to transfer thermal energy away from the core. What effect will those processes have on a person in a [latex]40.0\text{-}\text{°}\text{C}[/latex] hot tub?
Show Solution
Increasing circulation to the surface will warm the person, as the temperature of the water is warmer than human body temperature. Sweating will cause no evaporative cooling under water or in the humid air immediately above the tub.
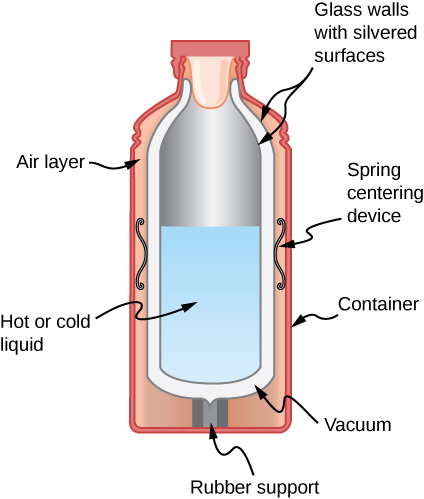
Shown below is a cut-away drawing of a thermos bottle (also known as a Dewar flask), which is a device designed specifically to slow down all forms of heat transfer. Explain the functions of the various parts, such as the vacuum, the silvering of the walls, the thin-walled long glass neck, the rubber support, the air layer, and the stopper.
Some electric stoves have a flat ceramic surface with heating elements hidden beneath. A pot placed over a heating element will be heated, while the surface only a few centimeters away is safe to touch. Why is ceramic, with a conductivity less than that of a metal but greater than that of a good insulator, an ideal choice for the stove top?
Show Solution
It spread the heat over the area above the heating elements, evening the temperature there, but does not spread the heat much beyond the heating elements.
Loose-fitting white clothing covering most of the body, shown below, is ideal for desert dwellers, both in the hot Sun and during cold evenings. Explain how such clothing is advantageous during both day and night.

One way to make a fireplace more energy-efficient is to have room air circulate around the outside of the fire box and back into the room. Detail the methods of heat transfer involved.
Show Solution
Heat is conducted from the fire through the fire box to the circulating air and then convected by the air into the room (forced convection).
On cold, clear nights horses will sleep under the cover of large trees. How does this help them keep warm?
When watching a circus during the day in a large, dark-colored tent, you sense significant heat transfer from the tent. Explain why this occurs.
Show Solution
The tent is heated by the Sun and transfers heat to you by all three processes, especially radiation.
Satellites designed to observe the radiation from cold (3 K) dark space have sensors that are shaded from the Sun, Earth, and the Moon and are cooled to very low temperatures. Why must the sensors be at low temperature?
Why are thermometers that are used in weather stations shielded from the sunshine? What does a thermometer measure if it is shielded from the sunshine? What does it measure if it is not?
Show Solution
If shielded, it measures the air temperature. If not, it measures the combined effect of air temperature and net radiative heat gain from the Sun.
Putting a lid on a boiling pot greatly reduces the heat transfer necessary to keep it boiling. Explain why.
Your house will be empty for a while in cold weather, and you want to save energy and money. Should you turn the thermostat down to the lowest level that will protect the house from damage such as freezing pipes, or leave it at the normal temperature? (If you don’t like coming back to a cold house, imagine that a timer controls the heating system so the house will be warm when you get back.) Explain your answer.
Show Solution
Turn the thermostat down. To have the house at the normal temperature, the heating system must replace all the heat that was lost. For all three mechanisms of heat transfer, the greater the temperature difference between inside and outside, the more heat is lost and must be replaced. So the house should be at the lowest temperature that does not allow freezing damage.
You pour coffee into an unlidded cup, intending to drink it 5 minutes later. You can add cream when you pour the cup or right before you drink it. (The cream is at the same temperature either way. Assume that the cream and coffee come into thermal equilibrium with each other very quickly.) Which way will give you hotter coffee? What feature of this question is different from the previous one?
Broiling is a method of cooking by radiation, which produces somewhat different results from cooking by conduction or convection. A gas flame or electric heating element produces a very high temperature close to the food and above it. Why is radiation the dominant heat-transfer method in this situation?
Show Solution
Air is a good insulator, so there is little conduction, and the heated air rises, so there is little convection downward.
On a cold winter morning, why does the metal of a bike feel colder than the wood of a porch?
Problems
(a) Calculate the rate of heat conduction through house walls that are 13.0 cm thick and have an average thermal conductivity twice that of glass wool. Assume there are no windows or doors. The walls’ surface area is [latex]120\phantom{\rule{0.2em}{0ex}}{\text{m}}^{2}[/latex] and their inside surface is at [latex]18.0\phantom{\rule{0.2em}{0ex}}\text{°}\text{C}[/latex], while their outside surface is at [latex]5.00\phantom{\rule{0.2em}{0ex}}\text{°}\text{C}[/latex]. (b) How many 1-kW room heaters would be needed to balance the heat transfer due to conduction?
Show Solution
a. [latex]1.01\phantom{\rule{0.2em}{0ex}}×\phantom{\rule{0.2em}{0ex}}{10}^{3}\phantom{\rule{0.2em}{0ex}}\text{W}[/latex]; b. One 1-kilowatt room heater is needed.
The rate of heat conduction out of a window on a winter day is rapid enough to chill the air next to it. To see just how rapidly the windows transfer heat by conduction, calculate the rate of conduction in watts through a [latex]3.00{\text{-m}}^{2}[/latex] window that is 0.634 cm thick (1/4 in.) if the temperatures of the inner and outer surfaces are [latex]5.00\phantom{\rule{0.2em}{0ex}}\text{°}\text{C}[/latex] and [latex]-10.0\phantom{\rule{0.2em}{0ex}}\text{°}\text{C}[/latex], respectively. (This rapid rate will not be maintained—the inner surface will cool, even to the point of frost formation.)
Calculate the rate of heat conduction out of the human body, assuming that the core internal temperature is [latex]37.0\phantom{\rule{0.2em}{0ex}}\text{°}\text{C}[/latex], the skin temperature is [latex]34.0\phantom{\rule{0.2em}{0ex}}\text{°}\text{C}[/latex], the thickness of the fatty tissues between the core and the skin averages 1.00 cm, and the surface area is [latex]1.40\phantom{\rule{0.2em}{0ex}}{\text{m}}^{2}[/latex].
Show Solution
84.0 W
Suppose you stand with one foot on ceramic flooring and one foot on a wool carpet, making contact over an area of [latex]80.0\phantom{\rule{0.2em}{0ex}}{\text{cm}}^{2}[/latex] with each foot. Both the ceramic and the carpet are 2.00 cm thick and are [latex]10.0\phantom{\rule{0.2em}{0ex}}\text{°}\text{C}[/latex] on their bottom sides. At what rate must heat transfer occur from each foot to keep the top of the ceramic and carpet at [latex]33.0\phantom{\rule{0.2em}{0ex}}\text{°}\text{C}[/latex]?
A man consumes 3000 kcal of food in one day, converting most of it to thermal energy to maintain body temperature. If he loses half this energy by evaporating water (through breathing and sweating), how many kilograms of water evaporate?
Show Solution
2.59 kg
A firewalker runs across a bed of hot coals without sustaining burns. Calculate the heat transferred by conduction into the sole of one foot of a firewalker given that the bottom of the foot is a 3.00-mm-thick callus with a conductivity at the low end of the range for wood and its density is [latex]300\phantom{\rule{0.2em}{0ex}}{\text{kg/m}}^{3}[/latex]. The area of contact is [latex]25.0\phantom{\rule{0.2em}{0ex}}{\text{cm}}^{2},[/latex] the temperature of the coals is [latex]700\phantom{\rule{0.2em}{0ex}}\text{°}\text{C}[/latex], and the time in contact is 1.00 s. Ignore the evaporative cooling of sweat.
(a) What is the rate of heat conduction through the 3.00-cm-thick fur of a large animal having a [latex]1.40{\text{-m}}^{2}[/latex] surface area? Assume that the animal’s skin temperature is [latex]32.0\phantom{\rule{0.2em}{0ex}}\text{°}\text{C}[/latex], that the air temperature is [latex]-5.00\phantom{\rule{0.2em}{0ex}}\text{°}\text{C}[/latex], and that fur has the same thermal conductivity as air. (b) What food intake will the animal need in one day to replace this heat transfer?
Show Solution
a. 39.7 W; b. 820 kcal
A walrus transfers energy by conduction through its blubber at the rate of 150 W when immersed in [latex]-1.00\phantom{\rule{0.2em}{0ex}}\text{°}\text{C}[/latex] water. The walrus’s internal core temperature is [latex]37.0\phantom{\rule{0.2em}{0ex}}\text{°}\text{C}[/latex], and it has a surface area of [latex]2.00\phantom{\rule{0.2em}{0ex}}{\text{m}}^{2}[/latex]. What is the average thickness of its blubber, which has the conductivity of fatty tissues without blood?
Compare the rate of heat conduction through a 13.0-cm-thick wall that has an area of [latex]10.0\phantom{\rule{0.2em}{0ex}}{\text{m}}^{2}[/latex] and a thermal conductivity twice that of glass wool with the rate of heat conduction through a 0.750-cm-thick window that has an area of [latex]2.00\phantom{\rule{0.2em}{0ex}}{\text{m}}^{2}[/latex], assuming the same temperature difference across each.
Show Solution
[latex]\frac{Q}{t}=\frac{kA\left({T}_{2}-{T}_{1}\right)}{d}[/latex], so that
[latex]\frac{{\left(Q\text{/}t\right)}_{\text{wall}}}{{\left(Q\text{/}t\right)}_{\text{window}}}=\frac{{k}_{\text{wall}}{A}_{\text{wall}}{d}_{\text{window}}}{{k}_{\text{window}}{A}_{\text{window}}{d}_{\text{wall}}}=\frac{\left(2\phantom{\rule{0.2em}{0ex}}×\phantom{\rule{0.2em}{0ex}}0.042\phantom{\rule{0.2em}{0ex}}\text{J/s}·\text{m}·\text{°}\text{C}\right)\left(10.0\phantom{\rule{0.2em}{0ex}}{\text{m}}^{2}\right)\left(0.750\phantom{\rule{0.2em}{0ex}}×\phantom{\rule{0.2em}{0ex}}{10}^{-2}\text{m}\right)}{\left(0.84\phantom{\rule{0.2em}{0ex}}\text{J/s}·\text{m}·\text{°}\text{C}\right)\left(2.00\phantom{\rule{0.2em}{0ex}}{\text{m}}^{2}\right)\left(13.0\phantom{\rule{0.2em}{0ex}}×\phantom{\rule{0.2em}{0ex}}{10}^{-2}\text{m}\right)}[/latex]
This gives 0.0288 wall: window, or 35:1 window: wall
Suppose a person is covered head to foot by wool clothing with average thickness of 2.00 cm and is transferring energy by conduction through the clothing at the rate of 50.0 W. What is the temperature difference across the clothing, given the surface area is [latex]1.40\phantom{\rule{0.2em}{0ex}}{\text{m}}^{2}[/latex]?
Some stove tops are smooth ceramic for easy cleaning. If the ceramic is 0.600 cm thick and heat conduction occurs through the same area and at the same rate as computed in Example 1.11, what is the temperature difference across it? Ceramic has the same thermal conductivity as glass and brick.
Show Solution
[latex]\frac{Q}{t}=\frac{kA\left({T}_{2}-{T}_{1}\right)}{d}=\frac{kA\text{Δ}T}{d}⇒[/latex]
[latex]\text{Δ}T=\frac{d\left(Q\text{/}t\right)}{kA}=\frac{\left(6.00\phantom{\rule{0.2em}{0ex}}×\phantom{\rule{0.2em}{0ex}}{10}^{-3}\phantom{\rule{0.2em}{0ex}}\text{m}\right)\left(2256\phantom{\rule{0.2em}{0ex}}\text{W}\right)}{\left(0.84\phantom{\rule{0.2em}{0ex}}\text{J/s}·\text{m}·\text{°}\text{C}\right)\left(1.54\phantom{\rule{0.2em}{0ex}}×\phantom{\rule{0.2em}{0ex}}{10}^{-2}\phantom{\rule{0.2em}{0ex}}{\text{m}}^{2}\right)}=1046\phantom{\rule{0.2em}{0ex}}\text{°}\text{C}=1.05\phantom{\rule{0.2em}{0ex}}×\phantom{\rule{0.2em}{0ex}}{10}^{3}\text{K}[/latex]
One easy way to reduce heating (and cooling) costs is to add extra insulation in the attic of a house. Suppose a single-story cubical house already had 15 cm of fiberglass insulation in the attic and in all the exterior surfaces. If you added an extra 8.0 cm of fiberglass to the attic, by what percentage would the heating cost of the house drop? Take the house to have dimensions 10 m by 15 m by 3.0 m. Ignore air infiltration and heat loss through windows and doors, and assume that the interior is uniformly at one temperature and the exterior is uniformly at another.
Many decisions are made on the basis of the payback period: the time it will take through savings to equal the capital cost of an investment. Acceptable payback times depend upon the business or philosophy one has. (For some industries, a payback period is as small as 2 years.) Suppose you wish to install the extra insulation in the preceding problem. If energy cost [latex]\text{\$}1.00[/latex] per million joules and the insulation was $4.00 per square meter, then calculate the simple payback time. Take the average [latex]\text{Δ}T[/latex] for the 120-day heating season to be [latex]15.0\phantom{\rule{0.2em}{0ex}}\text{°}\text{C}.[/latex]
Show Solution
We found in the preceding problem that [latex]P=126\text{Δ}T\phantom{\rule{0.2em}{0ex}}\text{W}·\text{°}\text{C}[/latex] as baseline energy use. So the total heat loss during this period is [latex]Q=\left(126\phantom{\rule{0.2em}{0ex}}\text{J/s}·\text{°}\text{C}\right)\left(15.0\phantom{\rule{0.2em}{0ex}}\text{°}\text{C}\right)\left(120\phantom{\rule{0.2em}{0ex}}\text{days}\right)\left(86.4\phantom{\rule{0.2em}{0ex}}×\phantom{\rule{0.2em}{0ex}}{10}^{3}\phantom{\rule{0.2em}{0ex}}\text{s/day}\right)=1960\phantom{\rule{0.2em}{0ex}}×\phantom{\rule{0.2em}{0ex}}{10}^{6}\phantom{\rule{0.2em}{0ex}}\text{J}[/latex]. At the cost of $1/MJ, the cost is $1960. From an earlier problem, the savings is 12% or $235/y. We need [latex]150\phantom{\rule{0.2em}{0ex}}{\text{m}}^{2}[/latex] of insulation in the attic. At [latex]\$4\text{/}{\text{m}}^{2}[/latex], this is a $500 cost. So the payback period is [latex]\$600\text{/}\left(\$235\text{/}\text{y}\right)=2.6\phantom{\rule{0.2em}{0ex}}\text{years}[/latex] (excluding labor costs).
Additional Problems
In 1701, the Danish astronomer Ole Rømer proposed a temperature scale with two fixed points, freezing water at 7.5 degrees, and boiling water at 60.0 degrees. What is the boiling point of oxygen, 90.2 K, on the Rømer scale?
What is the percent error of thinking the melting point of tungsten is [latex]3695\phantom{\rule{0.2em}{0ex}}\text{°}\text{C}[/latex] instead of the correct value of 3695 K?
Show Solution
[latex]7.39%[/latex]
An engineer wants to design a structure in which the difference in length between a steel beam and an aluminum beam remains at 0.500 m regardless of temperature, for ordinary temperatures. What must the lengths of the beams be?
How much stress is created in a steel beam if its temperature changes from [latex]–15\phantom{\rule{0.2em}{0ex}}\text{°}\text{C}[/latex] to [latex]40\phantom{\rule{0.2em}{0ex}}\text{°}\text{C}[/latex] but it cannot expand? For steel, the Young’s modulus [latex]Y=210\phantom{\rule{0.2em}{0ex}}×\phantom{\rule{0.2em}{0ex}}{10}^{9}\phantom{\rule{0.2em}{0ex}}{\text{N/m}}^{2}[/latex] from Stress, Strain, and Elastic Modulus. (Ignore the change in area resulting from the expansion.)
Show Solution
[latex]\frac{F}{A}=\left(210\phantom{\rule{0.2em}{0ex}}×\phantom{\rule{0.2em}{0ex}}{10}^{9}\phantom{\rule{0.2em}{0ex}}\text{Pa}\right)\left(12\phantom{\rule{0.2em}{0ex}}×\phantom{\rule{0.2em}{0ex}}{10}^{-6}\text{/}\text{°}\text{C}\right)\left(40\phantom{\rule{0.2em}{0ex}}\text{°}\text{C}-\left(-15\phantom{\rule{0.2em}{0ex}}\text{°}\text{C}\right)\right)=1.4\phantom{\rule{0.2em}{0ex}}×\phantom{\rule{0.2em}{0ex}}{10}^{8}\phantom{\rule{0.2em}{0ex}}{\text{N/m}}^{2}[/latex].
A brass rod [latex]\left(Y=90\phantom{\rule{0.2em}{0ex}}×\phantom{\rule{0.2em}{0ex}}{10}^{9}\phantom{\rule{0.2em}{0ex}}{\text{N/m}}^{2}\right),[/latex] with a diameter of 0.800 cm and a length of 1.20 m when the temperature is [latex]25\phantom{\rule{0.2em}{0ex}}\text{°}\text{C}[/latex], is fixed at both ends. At what temperature is the force in it at 36,000 N?
A mercury thermometer still in use for meteorology has a bulb with a volume of [latex]0.780\phantom{\rule{0.2em}{0ex}}{\text{cm}}^{3}[/latex] and a tube for the mercury to expand into of inside diameter 0.130 mm. (a) Neglecting the thermal expansion of the glass, what is the spacing between marks [latex]1\phantom{\rule{0.2em}{0ex}}\text{°}\text{C}[/latex] apart? (b) If the thermometer is made of ordinary glass (not a good idea), what is the spacing?
Show Solution
a. [latex]1.06[/latex] cm; b. [latex]1.11[/latex] cm
Even when shut down after a period of normal use, a large commercial nuclear reactor transfers thermal energy at the rate of 150 MW by the radioactive decay of fission products. This heat transfer causes a rapid increase in temperature if the cooling system fails ([latex]1\phantom{\rule{0.2em}{0ex}}\text{watt}=1\phantom{\rule{0.2em}{0ex}}\text{joule/second}[/latex] or [latex]1\phantom{\rule{0.2em}{0ex}}\text{W}=1\phantom{\rule{0.2em}{0ex}}\text{J/s}[/latex] and
[latex]1\phantom{\rule{0.2em}{0ex}}\text{MW}=1\phantom{\rule{0.2em}{0ex}}\text{megawatt}[/latex]). (a) Calculate the rate of temperature increase in degrees Celsius per second [latex]\left(\text{°}\text{C/s}\right)[/latex] if the mass of the reactor core is [latex]1.60\phantom{\rule{0.2em}{0ex}}×\phantom{\rule{0.2em}{0ex}}{10}^{5}\phantom{\rule{0.2em}{0ex}}\text{kg}[/latex] and it has an average specific heat of [latex]0.3349\phantom{\rule{0.2em}{0ex}}\text{kJ/kg}·\text{°}\text{C}[/latex]. (b) How long would it take to obtain a temperature increase of [latex]2000\phantom{\rule{0.2em}{0ex}}\text{°}\text{C}[/latex], which could cause some metals holding the radioactive materials to melt? (The initial rate of temperature increase would be greater than that calculated here because the heat transfer is concentrated in a smaller mass. Later, however, the temperature increase would slow down because the 500,000-kg steel containment vessel would also begin to heat up.)
You leave a pastry in the refrigerator on a plate and ask your roommate to take it out before you get home so you can eat it at room temperature, the way you like it. Instead, your roommate plays video games for hours. When you return, you notice that the pastry is still cold, but the game console has become hot. Annoyed, and knowing that the pastry will not be good if it is microwaved, you warm up the pastry by unplugging the console and putting it in a clean trash bag (which acts as a perfect calorimeter) with the pastry on the plate. After a while, you find that the equilibrium temperature is a nice, warm [latex]38.3\phantom{\rule{0.2em}{0ex}}\text{°}\text{C}[/latex]. You know that the game console has a mass of 2.1 kg. Approximate it as having a uniform initial temperature of [latex]45\phantom{\rule{0.2em}{0ex}}\text{°}\text{C}[/latex]. The pastry has a mass of 0.16 kg and a specific heat of [latex]3.0\phantom{\rule{0.2em}{0ex}}\text{k}\phantom{\rule{0.2em}{0ex}}\text{J/}\left(\text{kg}·\text{ºC}\right),[/latex] and is at a uniform initial temperature of [latex]4.0\phantom{\rule{0.2em}{0ex}}\text{°}\text{C}[/latex]. The plate is at the same temperature and has a mass of 0.24 kg and a specific heat of [latex]0.90\phantom{\rule{0.2em}{0ex}}\text{J/}\left(\text{kg}·\text{ºC}\right)[/latex]. What is the specific heat of the console?
Show Solution
[latex]1.7\phantom{\rule{0.2em}{0ex}}\text{kJ/}\left(\text{kg}·\text{ºC}\right)[/latex]
Two solid spheres, A and B, made of the same material, are at temperatures of [latex]0\phantom{\rule{0.2em}{0ex}}\text{°}\text{C}[/latex] and [latex]100\phantom{\rule{0.2em}{0ex}}\text{°}\text{C}[/latex], respectively. The spheres are placed in thermal contact in an ideal calorimeter, and they reach an equilibrium temperature of [latex]20\phantom{\rule{0.2em}{0ex}}\text{°}\text{C}[/latex]. Which is the bigger sphere? What is the ratio of their diameters?
In some countries, liquid nitrogen is used on dairy trucks instead of mechanical refrigerators. A 3.00-hour delivery trip requires 200 L of liquid nitrogen, which has a density of [latex]808\phantom{\rule{0.2em}{0ex}}{\text{kg/m}}^{3}.[/latex] (a) Calculate the heat transfer necessary to evaporate this amount of liquid nitrogen and raise its temperature to [latex]3.00\phantom{\rule{0.2em}{0ex}}\text{°}\text{C}[/latex]. (Use [latex]{c}_{\text{P}}[/latex] and assume it is constant over the temperature range.) This value is the amount of cooling the liquid nitrogen supplies. (b) What is this heat transfer rate in kilowatt-hours? (c) Compare the amount of cooling obtained from melting an identical mass of [latex]0\text{-}\text{°}\text{C}[/latex] ice with that from evaporating the liquid nitrogen.
Show Solution
a. [latex]1.57\phantom{\rule{0.2em}{0ex}}×\phantom{\rule{0.2em}{0ex}}{10}^{4}\phantom{\rule{0.2em}{0ex}}\text{kcal}[/latex]; b. [latex]18.3\phantom{\rule{0.2em}{0ex}}\text{kW}·\text{h}[/latex]; c. [latex]1.29\phantom{\rule{0.2em}{0ex}}×\phantom{\rule{0.2em}{0ex}}{10}^{4}\phantom{\rule{0.2em}{0ex}}\text{kcal}[/latex]
Some gun fanciers make their own bullets, which involves melting lead and casting it into lead slugs. How much heat transfer is needed to raise the temperature and melt 0.500 kg of lead, starting from [latex]25.0\phantom{\rule{0.2em}{0ex}}\text{°}\text{C}[/latex]?
A 0.800-kg iron cylinder at a temperature of [latex]1.00\phantom{\rule{0.2em}{0ex}}×\phantom{\rule{0.2em}{0ex}}{10}^{3}\phantom{\rule{0.2em}{0ex}}\text{°}\text{C}[/latex] is dropped into an insulated chest of 1.00 kg of ice at its melting point. What is the final temperature, and how much ice has melted?
Show Solution
[latex]6.3\phantom{\rule{0.2em}{0ex}}\text{°}\text{C}[/latex]. All of the ice melted.
Repeat the preceding problem with 2.00 kg of ice instead of 1.00 kg.
Repeat the preceding problem with 0.500 kg of ice, assuming that the ice is initially in a copper container of mass 1.50 kg in equilibrium with the ice.
Show Solution
[latex]63.9\phantom{\rule{0.2em}{0ex}}\text{°}\text{C}[/latex], all the ice melted
A 30.0-g ice cube at its melting point is dropped into an aluminum calorimeter of mass 100.0 g in equilibrium at [latex]24.0\phantom{\rule{0.2em}{0ex}}\text{°}\text{C}[/latex] with 300.0 g of an unknown liquid. The final temperature is [latex]4.0\phantom{\rule{0.2em}{0ex}}\text{°}\text{C}[/latex]. What is the heat capacity of the liquid?
(a) Calculate the rate of heat conduction through a double-paned window that has a [latex]1.50{\text{-m}}^{2}[/latex] area and is made of two panes of 0.800-cm-thick glass separated by a 1.00-cm air gap. The inside surface temperature is [latex]15.0\phantom{\rule{0.2em}{0ex}}\text{°}\text{C},[/latex] while that on the outside is [latex]-10.0\phantom{\rule{0.2em}{0ex}}\text{°}\text{C}.[/latex] (Hint: There are identical temperature drops across the two glass panes. First find these and then the temperature drop across the air gap. This problem ignores the increased heat transfer in the air gap due to convection.) (b) Calculate the rate of heat conduction through a 1.60-cm-thick window of the same area and with the same temperatures. Compare your answer with that for part (a).
Show Solution
a. 83 W; b. [latex]1.97\phantom{\rule{0.2em}{0ex}}×\phantom{\rule{0.2em}{0ex}}{10}^{3}\phantom{\rule{0.2em}{0ex}}\text{W}[/latex]; The single-pane window has a rate of heat conduction equal to 1969/83, or 24 times that of a double-pane window.
(a) An exterior wall of a house is 3 m tall and 10 m wide. It consists of a layer of drywall with an R factor of 0.56, a layer 3.5 inches thick filled with fiberglass batts, and a layer of insulated siding with an R factor of 2.6. The wall is built so well that there are no leaks of air through it. When the inside of the wall is at [latex]22\phantom{\rule{0.2em}{0ex}}\text{°}\text{C}[/latex] and the outside is at [latex]-2\phantom{\rule{0.2em}{0ex}}\text{°}\text{C}[/latex], what is the rate of heat flow through the wall? (b) More realistically, the 3.5-inch space also contains 2-by-4 studs—wooden boards 1.5 inches by 3.5 inches oriented so that 3.5-inch dimension extends from the drywall to the siding. They are “on 16-inch centers,” that is, the centers of the studs are 16 inches apart. What is the heat current in this situation? Don’t worry about one stud more or less.
For the human body, what is the rate of heat transfer by conduction through the body’s tissue with the following conditions: the tissue thickness is 3.00 cm, the difference in temperature is [latex]2.00\phantom{\rule{0.2em}{0ex}}\text{°}\text{C}[/latex], and the skin area is [latex]1.50\phantom{\rule{0.2em}{0ex}}{\text{m}}^{2}[/latex]. How does this compare with the average heat transfer rate to the body resulting from an energy intake of about 2400 kcal per day? (No exercise is included.)
Show Solution
The rate of heat transfer by conduction is 20.0 W. On a daily basis, this is 1,728 kJ/day. Daily food intake is [latex]2400\phantom{\rule{0.2em}{0ex}}\text{kcal/d}\phantom{\rule{0.2em}{0ex}}×\phantom{\rule{0.2em}{0ex}}4186\phantom{\rule{0.2em}{0ex}}\text{J/kcal}=10,050\phantom{\rule{0.2em}{0ex}}\text{kJ/day}[/latex]. So only 17.2% of energy intake goes as heat transfer by conduction to the environment at this [latex]\text{Δ}T[/latex].
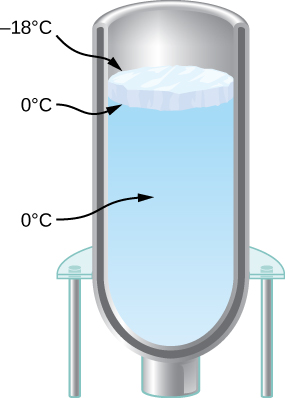
You have a Dewar flask (a laboratory vacuum flask) that has an open top and straight sides, as shown below. You fill it with water and put it into the freezer. It is effectively a perfect insulator, blocking all heat transfer, except on the top. After a time, ice forms on the surface of the water. The liquid water and the bottom surface of the ice, in contact with the liquid water, are at [latex]0\phantom{\rule{0.2em}{0ex}}\text{°}\text{C}[/latex]. The top surface of the ice is at the same temperature as the air in the freezer, [latex]-18\phantom{\rule{0.2em}{0ex}}\text{°}\text{C.}[/latex] Set the rate of heat flow through the ice equal to the rate of loss of heat of fusion as the water freezes. When the ice layer is 0.700 cm thick, find the rate in m/s at which the ice is thickening.
An infrared heater for a sauna has a surface area of [latex]0.050\phantom{\rule{0.2em}{0ex}}{\text{m}}^{2}[/latex] and an emissivity of 0.84. What temperature must it run at if the required power is 360 W? Neglect the temperature of the environment.
Show Solution
620 K
(a) Determine the power of radiation from the Sun by noting that the intensity of the radiation at the distance of Earth is [latex]1370\phantom{\rule{0.2em}{0ex}}{\text{W/m}}^{2}[/latex]. Hint: That intensity will be found everywhere on a spherical surface with radius equal to that of Earth’s orbit. (b) Assuming that the Sun’s temperature is 5780 K and that its emissivity is 1, find its radius.
Challenge Problems
A pendulum is made of a rod of length L and negligible mass, but capable of thermal expansion, and a weight of negligible size. (a) Show that when the temperature increases by dT, the period of the pendulum increases by a fraction [latex]\alpha LdT\text{/}2[/latex]. (b) A clock controlled by a brass pendulum keeps time correctly at [latex]10\phantom{\rule{0.2em}{0ex}}\text{°}\text{C}[/latex]. If the room temperature is [latex]30\phantom{\rule{0.2em}{0ex}}\text{°}\text{C}[/latex], does the clock run faster or slower? What is its error in seconds per day?
Show Solution
Denoting the period by P, we know [latex]P=2\pi \sqrt{L\text{/}g}.[/latex] When the temperature increases by dT, the length increases by [latex]\alpha LdT[/latex]. Then the new length is a. [latex]P=2\pi \sqrt{\frac{L+\alpha LdT}{g}}=2\pi \sqrt{\frac{L}{g}\left(1+\alpha dT\right)}=2\pi \sqrt{\frac{L}{g}}\left(1+\frac{1}{2}\alpha dT\right)=P\left(1+\frac{1}{2}\alpha dT\right)[/latex]
by the binomial expansion. b. The clock runs slower, as its new period is 1.00019 s. It loses 16.4 s per day.
At temperatures of a few hundred kelvins the specific heat capacity of copper approximately follows the empirical formula [latex]c=\alpha +\beta T+\delta {T}^{-2},[/latex] where [latex]\alpha =349\phantom{\rule{0.2em}{0ex}}\text{J/kg}·\text{K,}[/latex] [latex]\beta =0.107\phantom{\rule{0.2em}{0ex}}\text{J/kg}·{\text{K}}^{2},[/latex] and [latex]\delta =4.58\phantom{\rule{0.2em}{0ex}}×\phantom{\rule{0.2em}{0ex}}{10}^{5}\text{J}·\text{kg}·\text{K}\text{.}[/latex] How much heat is needed to raise the temperature of a 2.00-kg piece of copper from [latex]20\phantom{\rule{0.2em}{0ex}}\text{°}\text{C}[/latex] to [latex]250\phantom{\rule{0.2em}{0ex}}\text{°}\text{C}[/latex]?
In a calorimeter of negligible heat capacity, 200 g of steam at [latex]150\phantom{\rule{0.2em}{0ex}}\text{°}\text{C}[/latex] and 100 g of ice at [latex]-40\phantom{\rule{0.2em}{0ex}}\text{°}\text{C}[/latex] are mixed. The pressure is maintained at 1 atm. What is the final temperature, and how much steam, ice, and water are present?
Show Solution
The amount of heat to melt the ice and raise it to [latex]100\phantom{\rule{0.2em}{0ex}}\text{°}\text{C}[/latex] is not enough to condense the steam, but it is more than enough to lower the steam’s temperature by [latex]50\phantom{\rule{0.2em}{0ex}}\text{°}\text{C}[/latex], so the final state will consist of steam and liquid water in equilibrium, and the final temperature is [latex]100\phantom{\rule{0.2em}{0ex}}\text{°}\text{C}[/latex]; 9.5 g of steam condenses, so the final state contains 49.5 g of steam and 40.5 g of liquid water.
An astronaut performing an extra-vehicular activity (space walk) shaded from the Sun is wearing a spacesuit that can be approximated as perfectly white [latex]\left(e=0\right)[/latex] except for a [latex]5\phantom{\rule{0.2em}{0ex}}\text{cm}\phantom{\rule{0.2em}{0ex}}×\phantom{\rule{0.2em}{0ex}}8\phantom{\rule{0.2em}{0ex}}\text{cm}[/latex] patch in the form of the astronaut’s national flag. The patch has emissivity 0.300. The spacesuit under the patch is 0.500 cm thick, with a thermal conductivity [latex]k=0.0600\phantom{\rule{0.2em}{0ex}}\text{W/m}\phantom{\rule{0.2em}{0ex}}\text{°}\text{C}[/latex], and its inner surface is at a temperature of [latex]20.0\phantom{\rule{0.2em}{0ex}}\text{°}\text{C}[/latex]. What is the temperature of the patch, and what is the rate of heat loss through it? Assume the patch is so thin that its outer surface is at the same temperature as the outer surface of the spacesuit under it. Also assume the temperature of outer space is 0 K. You will get an equation that is very hard to solve in closed form, so you can solve it numerically with a graphing calculator, with software, or even by trial and error with a calculator.
Find the growth of an ice layer as a function of time in a Dewar flask as seen in Exercise 1.120. Call the thickness of the ice layer L. (a) Derive an equation for dL/dt in terms of L , the temperature T above the ice, and the properties of ice (which you can leave in symbolic form instead of substituting the numbers). (b) Solve this differential equation assuming that at [latex]t=0[/latex], you have [latex]L=0.[/latex] If you have studied differential equations, you will know a technique for solving equations of this type: manipulate the equation to get dL/dt multiplied by a (very simple) function of L on one side, and integrate both sides with respect to time. Alternatively, you may be able to use your knowledge of the derivatives of various functions to guess the solution, which has a simple dependence on t. (c) Will the water eventually freeze to the bottom of the flask?
Show Solution
a. [latex]dL\text{/}dT=kT\text{/}\rho L[/latex]; b. [latex]L=\sqrt{2kTt\text{/}\rho {L}_{\text{f}}}[/latex]; c. yes
As the very first rudiment of climatology, estimate the temperature of Earth. Assume it is a perfect sphere and its temperature is uniform. Ignore the greenhouse effect. Thermal radiation from the Sun has an intensity (the “solar constant” S) of about [latex]1370\phantom{\rule{0.2em}{0ex}}{\text{W/m}}^{2}[/latex] at the radius of Earth’s orbit. (a) Assuming the Sun’s rays are parallel, what area must S be multiplied by to get the total radiation intercepted by Earth? It will be easiest to answer in terms of Earth’s radius, R. (b) Assume that Earth reflects about 30% of the solar energy it intercepts. In other words, Earth has an albedo with a value of [latex]A=0.3[/latex]. In terms of S, A, and R, what is the rate at which Earth absorbs energy from the Sun? (c) Find the temperature at which Earth radiates energy at the same rate. Assume that at the infrared wavelengths where it radiates, the emissivity e is 1. Does your result show that the greenhouse effect is important? (d) How does your answer depend on the the area of Earth?
Let’s stop ignoring the greenhouse effect and incorporate it into the previous problem in a very rough way. Assume the atmosphere is a single layer, a spherical shell around Earth, with an emissivity [latex]e=0.77[/latex] (chosen simply to give the right answer) at infrared wavelengths emitted by Earth and by the atmosphere. However, the atmosphere is transparent to the Sun’s radiation (that is, assume the radiation is at visible wavelengths with no infrared), so the Sun’s radiation reaches the surface. The greenhouse effect comes from the difference between the atmosphere’s transmission of visible light and its rather strong absorption of infrared. Note that the atmosphere’s radius is not significantly different from Earth’s, but since the atmosphere is a layer above Earth, it emits radiation both upward and downward, so it has twice Earth’s area. There are three radiative energy transfers in this problem: solar radiation absorbed by Earth’s surface; infrared radiation from the surface, which is absorbed by the atmosphere according to its emissivity; and infrared radiation from the atmosphere, half of which is absorbed by Earth and half of which goes out into space. Apply the method of the previous problem to get an equation for Earth’s surface and one for the atmosphere, and solve them for the two unknown temperatures, surface and atmosphere.
- In terms of Earth’s radius, the constant [latex]\sigma[/latex], and the unknown temperature [latex]{T}_{s}[/latex] of the surface, what is the power of the infrared radiation from the surface?
- What is the power of Earth’s radiation absorbed by the atmosphere?
- In terms of the unknown temperature [latex]{T}_{e}[/latex] of the atmosphere, what is the power radiated from the atmosphere?
- Write an equation that says the power of the radiation the atmosphere absorbs from Earth equals the power of the radiation it emits.
- Half of the power radiated by the atmosphere hits Earth. Write an equation that says that the power Earth absorbs from the atmosphere and the Sun equals the power that it emits.
- Solve your two equations for the unknown temperature of Earth.
For steps that make this model less crude, see for example the lectures by Paul O’Gorman.
Show Solution
a. [latex]4\left(\pi {R}^{2}\right){T}_{\text{s}}{}^{4}[/latex]; b. [latex]4e\sigma \pi {R}^{2}{T}_{\text{s}}{}^{4}[/latex]; c. [latex]8e\sigma \pi {R}^{2}{T}_{\text{e}}{}^{4}[/latex]; d. [latex]{T}_{s}^{4}=2{T}_{e}^{4}[/latex]; e. [latex]e\sigma {T}_{\text{s}}^{4}+\frac{1}{4}\left(1-A\right)S=\sigma {T}_{\text{s}}^{4}[/latex]; f. [latex]288K[/latex]
Glossary
- conduction
- heat transfer through stationary matter by physical contact
- convection
- heat transfer by the macroscopic movement of fluid
- emissivity
- measure of how well an object radiates
- greenhouse effect
- warming of the earth that is due to gases such as carbon dioxide and methane that absorb infrared radiation from Earth’s surface and reradiate it in all directions, thus sending some of it back toward Earth
- net rate of heat transfer by radiation
- [latex]{P}_{\text{net}}=\sigma eA\left({T}_{2}{}^{4}-{T}_{1}{}^{4}\right)[/latex]
- radiation
- energy transferred by electromagnetic waves directly as a result of a temperature difference
- rate of conductive heat transfer
- rate of heat transfer from one material to another
- Stefan-Boltzmann law of radiation
- [latex]P=\sigma Ae{T}^{4},[/latex] where [latex]\sigma =5.67\phantom{\rule{0.2em}{0ex}}×\phantom{\rule{0.2em}{0ex}}{10}^{-8}\phantom{\rule{0.2em}{0ex}}\text{J/s}·{\text{m}}^{2}·{\text{K}}^{4}[/latex] is the Stefan-Boltzmann constant, A is the surface area of the object, T is the absolute temperature, and e is the emissivity
- thermal conductivity
- property of a material describing its ability to conduct heat
Licenses and Attributions
Mechanisms of Heat Transfer. Authored by: OpenStax College. Located at: https://openstax.org/books/university-physics-volume-2/pages/1-6-mechanisms-of-heat-transfer. License: CC BY: Attribution. License Terms: Download for free at https://openstax.org/books/university-physics-volume-2/pages/1-introduction

