Chapter 9. Current and Resistance
9.5 Electrical Energy and Power
Learning Objectives
By the end of this section, you will be able to:
- Express electrical power in terms of the voltage and the current
- Describe the power dissipated by a resistor in an electric circuit
- Calculate the energy efficiency and cost effectiveness of appliances and equipment
In an electric circuit, electrical energy is continuously converted into other forms of energy. For example, when a current flows in a conductor, electrical energy is converted into thermal energy within the conductor. The electrical field, supplied by the voltage source, accelerates the free electrons, increasing their kinetic energy for a short time. This increased kinetic energy is converted into thermal energy through collisions with the ions of the lattice structure of the conductor. In Work and Kinetic Energy, we defined power as the rate at which work is done by a force measured in watts. Power can also be defined as the rate at which energy is transferred. In this section, we discuss the time rate of energy transfer, or power, in an electric circuit.
Power in Electric Circuits
Power is associated by many people with electricity. Power transmission lines might come to mind. We also think of light bulbs in terms of their power ratings in watts. What is the expression for electric power?
Let us compare a 25-W bulb with a 60-W bulb (Figure 9.23(a)). The 60-W bulb glows brighter than the 25-W bulb. Although it is not shown, a 60-W light bulb is also warmer than the 25-W bulb. The heat and light is produced by from the conversion of electrical energy. The kinetic energy lost by the electrons in collisions is converted into the internal energy of the conductor and radiation. How are voltage, current, and resistance related to electric power?

To calculate electric power, consider a voltage difference existing across a material (Figure 9.24). The electric potential [latex]{V}_{1}[/latex] is higher than the electric potential at [latex]{V}_{2}[/latex], and the voltage difference is negative [latex]V={V}_{2}-{V}_{1}[/latex]. As discussed in Electric Potential, an electrical field exists between the two potentials, which points from the higher potential to the lower potential. Recall that the electrical potential is defined as the potential energy per charge, [latex]V=\text{Δ}U\text{/}q[/latex], and the charge [latex]\text{Δ}Q[/latex] loses potential energy moving through the potential difference.
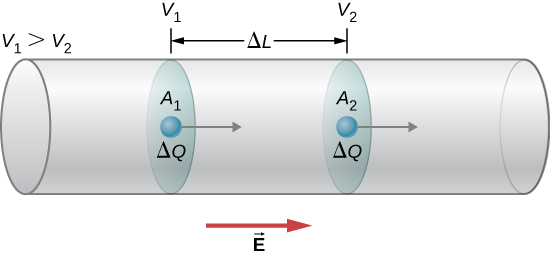
If the charge is positive, the charge experiences a force due to the electrical field [latex]\stackrel{\to }{\textbf{F}}=m\stackrel{\to }{\textbf{a}}=\text{Δ}Q\stackrel{\to }{\textbf{E}}[/latex]. This force is necessary to keep the charge moving. This force does not act to accelerate the charge through the entire distance [latex]\text{Δ}L[/latex] because of the interactions of the charge with atoms and free electrons in the material. The speed, and therefore the kinetic energy, of the charge do not increase during the entire trip across [latex]\text{Δ}L[/latex], and charge passing through area [latex]{A}_{2}[/latex] has the same drift velocity [latex]{v}_{\text{d}}[/latex] as the charge that passes through area [latex]{A}_{1}[/latex]. However, work is done on the charge, by the electrical field, which changes the potential energy. Since the change in the electrical potential difference is negative, the electrical field is found to be
The work done on the charge is equal to the electric force times the length at which the force is applied,
The charge moves at a drift velocity [latex]{v}_{\text{d}}[/latex] so the work done on the charge results in a loss of potential energy, but the average kinetic energy remains constant. The lost electrical potential energy appears as thermal energy in the material. On a microscopic scale, the energy transfer is due to collisions between the charge and the molecules of the material, which leads to an increase in temperature in the material. The loss of potential energy results in an increase in the temperature of the material, which is dissipated as radiation. In a resistor, it is dissipated as heat, and in a light bulb, it is dissipated as heat and light.
The power dissipated by the material as heat and light is equal to the time rate of change of the work:
With a resistor, the voltage drop across the resistor is dissipated as heat. Ohm’s law states that the voltage across the resistor is equal to the current times the resistance, [latex]V=IR[/latex]. The power dissipated by the resistor is therefore
If a resistor is connected to a battery, the power dissipated as radiant energy by the wires and the resistor is equal to [latex]P=IV={I}^{2}R=\frac{{V}^{2}}{R}[/latex]. The power supplied from the battery is equal to current times the voltage, [latex]P=IV[/latex].
Electric Power
The electric power gained or lost by any device has the form
The power dissipated by a resistor has the form
Different insights can be gained from the three different expressions for electric power. For example, [latex]P={V}^{2}\text{/}R[/latex] implies that the lower the resistance connected to a given voltage source, the greater the power delivered. Furthermore, since voltage is squared in [latex]P={V}^{2}\text{/}R[/latex], the effect of applying a higher voltage is perhaps greater than expected. Thus, when the voltage is doubled to a 25-W bulb, its power nearly quadruples to about 100 W, burning it out. If the bulb’s resistance remained constant, its power would be exactly 100 W, but at the higher temperature, its resistance is higher, too.
Example
Calculating Power in Electric Devices
A DC winch motor is rated at 20.00 A with a voltage of 115 V. When the motor is running at its maximum power, it can lift an object with a weight of 4900.00 N a distance of 10.00 m, in 30.00 s, at a constant speed. (a) What is the power consumed by the motor? (b) What is the power used in lifting the object? Ignore air resistance. (c) Assuming that the difference in the power consumed by the motor and the power used lifting the object are dissipated as heat by the resistance of the motor, estimate the resistance of the motor?
Strategy
(a) The power consumed by the motor can be found using [latex]P=IV[/latex]. (b) The power used in lifting the object at a constant speed can be found using [latex]P=Fv[/latex], where the speed is the distance divided by the time. The upward force supplied by the motor is equal to the weight of the object because the acceleration is constant. (c) The resistance of the motor can be found using [latex]P={I}^{2}R[/latex].
Solution
Show Answer
- The power consumed by the motor is equal to [latex]P=IV[/latex] and the current is given as 20.00 A and the voltage is 115.00 V:
[latex]P=IV=\left(20.00\phantom{\rule{0.2em}{0ex}}\text{A}\right)115.00\phantom{\rule{0.2em}{0ex}}\text{V}=2300.00\phantom{\rule{0.2em}{0ex}}\text{W}.[/latex] - The power used lifting the object is equal to [latex]P=Fv[/latex] where the force is equal to the weight of the object (1960 N) and the magnitude of the velocity is [latex]v=\frac{10.00\phantom{\rule{0.2em}{0ex}}\text{m}}{30.00\phantom{\rule{0.2em}{0ex}}\text{s}}=0.33\frac{\text{m}}{\text{s}}[/latex],
[latex]P=Fv=\left(4900\phantom{\rule{0.2em}{0ex}}\text{N}\right)0.33\phantom{\rule{0.2em}{0ex}}\text{m/s}=1633.33\phantom{\rule{0.2em}{0ex}}\text{W}.[/latex] - The difference in the power equals [latex]2300.00\phantom{\rule{0.2em}{0ex}}\text{W}-1633.33\phantom{\rule{0.2em}{0ex}}\text{W}=666.67\phantom{\rule{0.2em}{0ex}}\text{W}[/latex] and the resistance can be found using [latex]P={I}^{2}R[/latex]:
[latex]R=\frac{P}{{I}^{2}}=\frac{666.67\phantom{\rule{0.2em}{0ex}}\text{W}}{{\left(20.00\phantom{\rule{0.2em}{0ex}}\text{A}\right)}^{2}}=1.67\phantom{\rule{0.2em}{0ex}}\text{Ω}\phantom{\rule{0.2em}{0ex}}.[/latex]
Significance
The resistance of the motor is quite small. The resistance of the motor is due to many windings of copper wire. The power dissipated by the motor can be significant since the thermal power dissipated by the motor is proportional to the square of the current [latex]\left(P={I}^{2}R\right)[/latex].
Check Your Understanding
Electric motors have a reasonably high efficiency. A 100-hp motor can have an efficiency of 90% and a 1-hp motor can have an efficiency of 80%. Why is it important to use high-performance motors?
Show Solution
Even though electric motors are highly efficient 10–20% of the power consumed is wasted, not being used for doing useful work. Most of the 10–20% of the power lost is transferred into heat dissipated by the copper wires used to make the coils of the motor. This heat adds to the heat of the environment and adds to the demand on power plants providing the power. The demand on the power plant can lead to increased greenhouse gases, particularly if the power plant uses coal or gas as fuel.
A fuse (Figure 9.25) is a device that protects a circuit from currents that are too high. A fuse is basically a short piece of wire between two contacts. As we have seen, when a current is running through a conductor, the kinetic energy of the charge carriers is converted into thermal energy in the conductor. The piece of wire in the fuse is under tension and has a low melting point. The wire is designed to heat up and break at the rated current. The fuse is destroyed and must be replaced, but it protects the rest of the circuit. Fuses act quickly, but there is a small time delay while the wire heats up and breaks.

Circuit breakers are also rated for a maximum current, and open to protect the circuit, but can be reset. Circuit breakers react much faster. The operation of circuit breakers is not within the scope of this chapter and will be discussed in later chapters. Another method of protecting equipment and people is the ground fault circuit interrupter (GFCI), which is common in bathrooms and kitchens. The GFCI outlets respond very quickly to changes in current. These outlets open when there is a change in magnetic field produced by current-carrying conductors, which is also beyond the scope of this chapter and is covered in a later chapter.
The Cost of Electricity
The more electric appliances you use and the longer they are left on, the higher your electric bill. This familiar fact is based on the relationship between energy and power. You pay for the energy used. Since [latex]P=\frac{dE}{dt}[/latex], we see that
is the energy used by a device using power P for a time interval t. If power is delivered at a constant rate, then then the energy can be found by [latex]E=Pt[/latex]. For example, the more light bulbs burning, the greater P used; the longer they are on, the greater t is.
The energy unit on electric bills is the kilowatt-hour [latex]\left(\text{kW}·\text{h}\right)[/latex], consistent with the relationship [latex]E=Pt[/latex]. It is easy to estimate the cost of operating electrical appliances if you have some idea of their power consumption rate in watts or kilowatts, the time they are on in hours, and the cost per kilowatt-hour for your electric utility. Kilowatt-hours, like all other specialized energy units such as food calories, can be converted into joules. You can prove to yourself that [latex]1\phantom{\rule{0.2em}{0ex}}\text{kW}·\text{h}=3.6\phantom{\rule{0.2em}{0ex}}×\phantom{\rule{0.2em}{0ex}}{10}^{6}\phantom{\rule{0.2em}{0ex}}\text{J}[/latex].
The electrical energy (E) used can be reduced either by reducing the time of use or by reducing the power consumption of that appliance or fixture. This not only reduces the cost but also results in a reduced impact on the environment. Improvements to lighting are some of the fastest ways to reduce the electrical energy used in a home or business. About 20% of a home’s use of energy goes to lighting, and the number for commercial establishments is closer to 40%. Fluorescent lights are about four times more efficient than incandescent lights—this is true for both the long tubes and the compact fluorescent lights (CFLs). (See Figure 9.23(b).) Thus, a 60-W incandescent bulb can be replaced by a 15-W CFL, which has the same brightness and color. CFLs have a bent tube inside a globe or a spiral-shaped tube, all connected to a standard screw-in base that fits standard incandescent light sockets. (Original problems with color, flicker, shape, and high initial investment for CFLs have been addressed in recent years.)
The heat transfer from these CFLs is less, and they last up to 10 times longer than incandescent bulbs. The significance of an investment in such bulbs is addressed in the next example. New white LED lights (which are clusters of small LED bulbs) are even more efficient (twice that of CFLs) and last five times longer than CFLs.
Example
Calculating the Cost Effectiveness of LED Bulb
The typical replacement for a 100-W incandescent bulb is a 20-W LED bulb. The 20-W LED bulb can provide the same amount of light output as the 100-W incandescent light bulb. What is the cost savings for using the LED bulb in place of the incandescent bulb for one year, assuming $0.10 per kilowatt-hour is the average energy rate charged by the power company? Assume that the bulb is turned on for three hours a day.
Strategy
(a) Calculate the energy used during the year for each bulb, using [latex]E=Pt[/latex].
(b) Multiply the energy by the cost.
Solution
Show Answer
- Calculate the power for each bulb.
- Calculate the cost for each.
[latex]\begin{array}{cc}\hfill {\text{cost}}_{\text{Incandescent}}& =109.5\phantom{\rule{0.2em}{0ex}}\text{kW-h}\left(\frac{\$0.10}{\text{kW}·\text{h}}\right)=\$10.95\hfill \\ \hfill {\text{cost}}_{\text{LED}}& =21.90\phantom{\rule{0.2em}{0ex}}\text{kW-h}\left(\frac{\$0.10}{\text{kW}·\text{h}}\right)=\$2.19\hfill \end{array}.[/latex]
Significance
A LED bulb uses 80% less energy than the incandescent bulb, saving $8.76 over the incandescent bulb for one year. The LED bulb can cost $20.00 and the 100-W incandescent bulb can cost $0.75, which should be calculated into the computation. A typical lifespan of an incandescent bulb is 1200 hours and is 50,000 hours for the LED bulb. The incandescent bulb would last 1.08 years at 3 hours a day and the LED bulb would last 45.66 years. The initial cost of the LED bulb is high, but the cost to the home owner will be $0.69 for the incandescent bulbs versus $0.44 for the LED bulbs per year. (Note that the LED bulbs are coming down in price.) The cost savings per year is approximately $8.50, and that is just for one bulb.
Check Your Understanding
Is the efficiency of the various light bulbs the only consideration when comparing the various light bulbs?
Show Solution
No, the efficiency is a very important consideration of the light bulbs, but there are many other considerations. As mentioned above, the cost of the bulbs and the life span of the bulbs are important considerations. For example, CFL bulbs contain mercury, a neurotoxin, and must be disposed of as hazardous waste. When replacing incandescent bulbs that are being controlled by a dimmer switch with LED, the dimmer switch may need to be replaced. The dimmer switches for LED lights are comparably priced to the incandescent light switches, but this is an initial cost which should be considered. The spectrum of light should also be considered, but there is a broad range of color temperatures available, so you should be able to find one that fits your needs. None of these considerations mentioned are meant to discourage the use of LED or CFL light bulbs, but they are considerations.
Changing light bulbs from incandescent bulbs to CFL or LED bulbs is a simple way to reduce energy consumption in homes and commercial sites. CFL bulbs operate with a much different mechanism than do incandescent lights. The mechanism is complex and beyond the scope of this chapter, but here is a very general description of the mechanism. CFL bulbs contain argon and mercury vapor housed within a spiral-shaped tube. The CFL bulbs use a “ballast” that increases the voltage used by the CFL bulb. The ballast produce an electrical current, which passes through the gas mixture and excites the gas molecules. The excited gas molecules produce ultraviolet (UV) light, which in turn stimulates the fluorescent coating on the inside of the tube. This coating fluoresces in the visible spectrum, emitting visible light. Traditional fluorescent tubes and CFL bulbs had a short time delay of up to a few seconds while the mixture was being “warmed up” and the molecules reached an excited state. It should be noted that these bulbs do contain mercury, which is poisonous, but if the bulb is broken, the mercury is never released. Even if the bulb is broken, the mercury tends to remain in the fluorescent coating. The amount is also quite small and the advantage of the energy saving may outweigh the disadvantage of using mercury.
The CFL light bulbs are being replaced with LED light bulbs, where LED stands for “light-emitting diode.” The diode was briefly discussed as a nonohmic device, made of semiconducting material, which essentially permits current flow in one direction. LEDs are a special type of diode made of semiconducting materials infused with impurities in combinations and concentrations that enable the extra energy from the movement of the electrons during electrical excitation to be converted into visible light. Semiconducting devices will be explained in greater detail in Condensed Matter Physics.
Commercial LEDs are quickly becoming the standard for commercial and residential lighting, replacing incandescent and CFL bulbs. They are designed for the visible spectrum and are constructed from gallium doped with arsenic and phosphorous atoms. The color emitted from an LED depends on the materials used in the semiconductor and the current. In the early years of LED development, small LEDs found on circuit boards were red, green, and yellow, but LED light bulbs can now be programmed to produce millions of colors of light as well as many different hues of white light.
Comparison of Incandescent, CFL, and LED Light Bulbs
The energy savings can be significant when replacing an incandescent light bulb or a CFL light bulb with an LED light. Light bulbs are rated by the amount of power that the bulb consumes, and the amount of light output is measured in lumens. The lumen (lm) is the SI -derived unit of luminous flux and is a measure of the total quantity of visible light emitted by a source. A 60-W incandescent light bulb can be replaced with a 13- to 15-W CFL bulb or a 6- to 8-W LED bulb, all three of which have a light output of approximately 800 lm. A table of light output for some commonly used light bulbs appears in Table 9.2.
The life spans of the three types of bulbs are significantly different. An LED bulb has a life span of 50,000 hours, whereas the CFL has a lifespan of 8000 hours and the incandescent lasts a mere 1200 hours. The LED bulb is the most durable, easily withstanding rough treatment such as jarring and bumping. The incandescent light bulb has little tolerance to the same treatment since the filament and glass can easily break. The CFL bulb is also less durable than the LED bulb because of its glass construction. The amount of heat emitted is 3.4 btu/h for the 8-W LED bulb, 85 btu/h for the 60-W incandescent bulb, and 30 btu/h for the CFL bulb. As mentioned earlier, a major drawback of the CFL bulb is that it contains mercury, a neurotoxin, and must be disposed of as hazardous waste. From these data, it is easy to understand why the LED light bulb is quickly becoming the standard in lighting.
| Light Output (lumens) |
LED Light Bulbs (watts) |
Incandescent Light Bulbs (watts) |
CFL Light Bulbs (watts) |
|---|---|---|---|
| 450 | 4−5 | 40 | 9−13 |
| 800 | 6−8 | 60 | 13−15 |
| 1100 | 9−13 | 75 | 18−25 |
| 1600 | 16−20 | 100 | 23−30 |
| 2600 | 25−28 | 150 | 30−55 |
Summary of Relationships
In this chapter, we have discussed relationships between voltages, current, resistance, and power. Figure 9.26 shows a summary of the relationships between these measurable quantities for ohmic devices. (Recall that ohmic devices follow Ohm’s law [latex]V=IR[/latex].) For example, if you need to calculate the power, use the pink section, which shows that [latex]P=VI[/latex], [latex]P=\frac{{V}^{2}}{R}[/latex], and [latex]P={I}^{2}R[/latex].
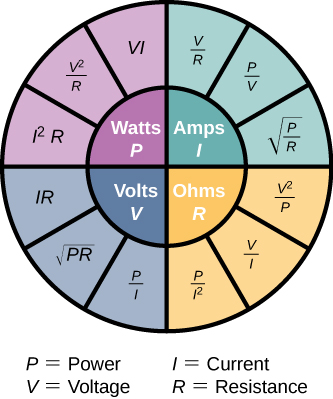
Which equation you use depends on what values you are given, or you measure. For example if you are given the current and the resistance, use [latex]P={I}^{2}R[/latex]. Although all the possible combinations may seem overwhelming, don’t forget that they all are combinations of just two equations, Ohm’s law [latex]\left(V=IR\right)[/latex] and power [latex]\left(P=IV\right)[/latex].
Summary
- Electric power is the rate at which electric energy is supplied to a circuit or consumed by a load.
- Power dissipated by a resistor depends on the square of the current through the resistor and is equal to [latex]P={I}^{2}R=\frac{{V}^{2}}{R}[/latex].
- The SI unit for electric power is the watt and the SI unit for electric energy is the joule. Another common unit for electric energy, used by power companies, is the kilowatt-hour (kW [latex]·[/latex] h).
- The total energy used over a time interval can be found by [latex]E=\int Pdt[/latex].
Conceptual Questions
Common household appliances are rated at 110 V, but power companies deliver voltage in the kilovolt range and then step the voltage down using transformers to 110 V to be used in homes. You will learn in later chapters that transformers consist of many turns of wire, which warm up as current flows through them, wasting some of the energy that is given off as heat. This sounds inefficient. Why do the power companies transport electric power using this method?
Show Solution
Although the conductors have a low resistance, the lines from the power company can be kilometers long. Using a high voltage reduces the current that is required to supply the power demand and that reduces line losses.
Your electric bill gives your consumption in units of kilowatt-hour (kW [latex]·[/latex] h). Does this unit represent the amount of charge, current, voltage, power, or energy you buy?
Resistors are commonly rated at [latex]\frac{1}{8}\text{W}[/latex], [latex]\frac{1}{4}\text{W}[/latex], [latex]\frac{1}{2}\text{W}[/latex], 1 W and 2 W for use in electrical circuits. If a current of [latex]I=2.00\phantom{\rule{0.2em}{0ex}}\text{A}[/latex] is accidentally passed through a [latex]R=1.00\phantom{\rule{0.2em}{0ex}}\text{Ω}[/latex] resistor rated at 1 W, what would be the most probable outcome? Is there anything that can be done to prevent such an accident?
Show Solution
The resistor would overheat, possibly to the point of causing the resistor to burn. Fuses are commonly added to circuits to prevent such accidents.
An immersion heater is a small appliance used to heat a cup of water for tea by passing current through a resistor. If the voltage applied to the appliance is doubled, will the time required to heat the water change? By how much? Is this a good idea?
Problems
A [latex]20.00\text{-V}[/latex] battery is used to supply current to a [latex]10\text{-k}\phantom{\rule{0.2em}{0ex}}\text{Ω}[/latex] resistor. Assume the voltage drop across any wires used for connections is negligible. (a) What is the current through the resistor? (b) What is the power dissipated by the resistor? (c) What is the power input from the battery, assuming all the electrical power is dissipated by the resistor? (d) What happens to the energy dissipated by the resistor?
Show Solution
a. [latex]I=2\phantom{\rule{0.2em}{0ex}}\text{mA}[/latex]; b. [latex]P=0.04\phantom{\rule{0.2em}{0ex}}\text{W}[/latex]; c. [latex]P=0.04\phantom{\rule{0.2em}{0ex}}\text{W}[/latex]; d. It is converted into heat.
What is the maximum voltage that can be applied to a [latex]10\text{-k}\phantom{\rule{0.2em}{0ex}}\text{Ω}[/latex] resistor rated at [latex]\frac{1}{4}\text{W}[/latex]?
A heater is being designed that uses a coil of 14-gauge nichrome wire to generate 300 W using a voltage of [latex]V=110\phantom{\rule{0.2em}{0ex}}\text{V}[/latex]. How long should the engineer make the wire?
Show Solution
[latex]\begin{array}{}\\ \\ P=\frac{{V}^{2}}{R}\hfill \\ R=40\phantom{\rule{0.2em}{0ex}}\text{Ω}\phantom{\rule{0.2em}{0ex}}\hfill \end{array}[/latex], [latex]\begin{array}{c}A=2.08{\text{mm}}^{2}\hfill \\ \rho =100\phantom{\rule{0.2em}{0ex}}×\phantom{\rule{0.2em}{0ex}}{10}^{-8}\phantom{\rule{0.2em}{0ex}}\text{Ω}\phantom{\rule{0.2em}{0ex}}·\text{m}\hfill \\ R=\rho \frac{L}{A}\hfill \\ L=83\phantom{\rule{0.2em}{0ex}}\text{m}\hfill \end{array}[/latex]
An alternative to CFL bulbs and incandescent bulbs are light-emitting diode (LED) bulbs. A 100-W incandescent bulb can be replaced by a 16-W LED bulb. Both produce 1600 lumens of light. Assuming the cost of electricity is $0.10 per kilowatt-hour, how much does it cost to run the bulb for one year if it runs for four hours a day?
The power dissipated by a resistor with a resistance of [latex]R=100\phantom{\rule{0.2em}{0ex}}\text{Ω}[/latex] is [latex]P=2.0\phantom{\rule{0.2em}{0ex}}\text{W}[/latex]. What are the current through and the voltage drop across the resistor?
Show Solution
[latex]I=0.14\phantom{\rule{0.2em}{0ex}}\text{A},\phantom{\rule{0.8em}{0ex}}V=14\phantom{\rule{0.2em}{0ex}}\text{V}[/latex]
Running late to catch a plane, a driver accidentally leaves the headlights on after parking the car in the airport parking lot. During takeoff, the driver realizes the mistake. Having just replaced the battery, the driver knows that the battery is a 12-V automobile battery, rated at 100 [latex]\text{A}·\text{h}[/latex]. The driver, knowing there is nothing that can be done, estimates how long the lights will shine, assuming there are two 12-V headlights, each rated at 40 W. What did the driver conclude?
A physics student has a single-occupancy dorm room. The student has a small refrigerator that runs with a current of 3.00 A and a voltage of 110 V, a lamp that contains a 100-W bulb, an overhead light with a 60-W bulb, and various other small devices adding up to 3.00 W. (a) Assuming the power plant that supplies 110 V electricity to the dorm is 10 km away and the two aluminum transmission cables use 0-gauge wire with a diameter of 8.252 mm, estimate the percentage of the total power supplied by the power company that is lost in the transmission. (b) What would be the result is the power company delivered the electric power at 110 kV?
Show Solution
a. [latex]\begin{array}{}\\ \\ I\approx 3.00\phantom{\rule{0.2em}{0ex}}\text{A}+\frac{100\phantom{\rule{0.2em}{0ex}}\text{W}}{110\phantom{\rule{0.2em}{0ex}}\text{V}}+\frac{60\phantom{\rule{0.2em}{0ex}}\text{W}}{110\phantom{\rule{0.2em}{0ex}}\text{V}}+\frac{3.00\phantom{\rule{0.2em}{0ex}}\text{W}}{110\phantom{\rule{0.2em}{0ex}}\text{V}}=4.48\phantom{\rule{0.2em}{0ex}}\text{A}\hfill \\ P=493\phantom{\rule{0.2em}{0ex}}\text{W}\hfill \\ R=9.91\phantom{\rule{0.2em}{0ex}}\text{Ω}\phantom{\rule{0.2em}{0ex}},\hfill \\ {P}_{\text{loss}}=200.\phantom{\rule{0.2em}{0ex}}\text{W}\hfill \\ \text{%}\text{loss}=40\text{%}\hfill \end{array}[/latex]
b. [latex]\begin{array}{c}P=493\phantom{\rule{0.2em}{0ex}}\text{W}\hfill \\ I=0.0045\phantom{\rule{0.2em}{0ex}}\text{A}\hfill \\ R=9.91\phantom{\rule{0.2em}{0ex}}\text{Ω}\phantom{\rule{0.2em}{0ex}}\hfill \\ {P}_{\text{loss}}=201\mu \phantom{\rule{0.2em}{0ex}}\text{W}\hfill \\ \text{%}\text{loss}=0.00004\text{%}\hfill \end{array}[/latex]
A 0.50-W, [latex]220\text{-}\phantom{\rule{0.2em}{0ex}}\text{Ω}[/latex] resistor carries the maximum current possible without damaging the resistor. If the current were reduced to half the value, what would be the power consumed?
Glossary
- electrical power
- time rate of change of energy in an electric circuit
Licenses and Attributions
Electrical Energy and Power. Authored by: OpenStax College. Located at: https://openstax.org/books/university-physics-volume-2/pages/9-5-electrical-energy-and-power. License: CC BY: Attribution. License Terms: Download for free at https://openstax.org/books/university-physics-volume-2/pages/1-introduction

