5.1 Electric Charge

Discoveries

You have probably experienced the phenomenon of static electricity: When you first take clothes out of a dryer, many (not all) of them tend to stick together; for some fabrics, they can be very difficult to separate. Another example occurs if you take a woolen sweater off quickly—you can feel (and hear) the static electricity pulling on your clothes, and perhaps even your hair. If you comb your hair on a dry day and then put the comb close to a thin stream of water coming out of a faucet, you will find that the water stream bends toward (is attracted to) the comb (Figure 5.2).

Suppose you bring the comb close to some small strips of paper; the strips of paper are attracted to the comb and even cling to it (Figure 5.3). In the kitchen, quickly pull a length of plastic cling wrap off the roll; it will tend to cling to most any nonmetallic material (such as plastic, glass, or food). If you rub a balloon on a wall for a few seconds, it will stick to the wall. Probably the most annoying effect of static electricity is getting shocked by a doorknob (or a friend) after shuffling your feet on some types of carpeting.

Many of these phenomena have been known for centuries. The ancient Greek philosopher Thales of Miletus (624–546 BCE) recorded that when amber (a hard, translucent, fossilized resin from extinct trees) was vigorously rubbed with a piece of fur, a force was created that caused the fur and the amber to be attracted to each other (Figure 5.4). Additionally, he found that the rubbed amber would not only attract the fur, and the fur attract the amber, but they both could affect other (nonmetallic) objects, even if not in contact with those objects (Figure 5.5).

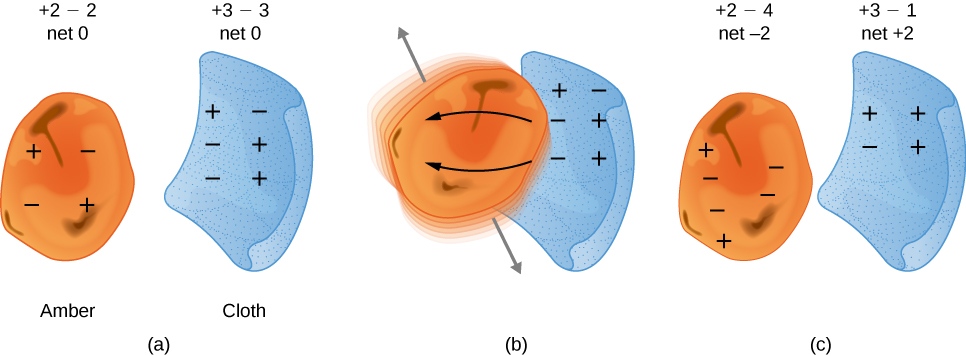
The English physicist William Gilbert (1544–1603) also studied this attractive force, using various substances. He worked with amber, and, in addition, he experimented with rock crystal and various precious and semi-precious gemstones. He also experimented with several metals. He found that the metals never exhibited this force, whereas the minerals did. Moreover, although an electrified amber rod would attract a piece of fur, it would repel another electrified amber rod; similarly, two electrified pieces of fur would repel each other.

This suggested there were two types of an electric property; this property eventually came to be called electric charge. The difference between the two types of electric charge is in the directions of the electric forces that each type of charge causes: These forces are repulsive when the same type of charge exists on two interacting objects and attractive when the charges are of opposite types. The SI unit of electric charge is the coulomb (C), after the French physicist Charles-Augustin de Coulomb (1736–1806).

The most peculiar aspect of this new force is that it does not require physical contact between the two objects in order to cause an acceleration. This is an example of a so-called “long-range” force. (Or, as Albert Einstein later phrased it, “action at a distance.”) With the exception of gravity, all other forces we have discussed so far act only when the two interacting objects actually touch.

The American physicist and statesman Benjamin Franklin found that he could concentrate charge in a “Leyden jar,” which was essentially a glass jar with two sheets of metal foil, one inside and one outside, with the glass between them (Figure 5.6). This created a large electric force between the two foil sheets.

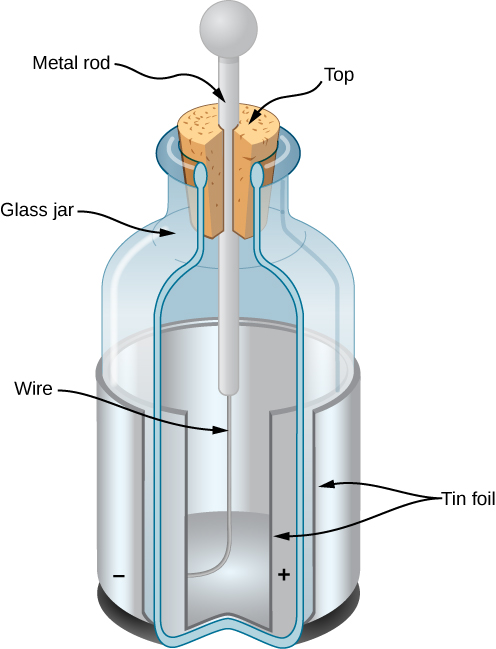
Franklin pointed out that the observed behavior could be explained by supposing that one of the two types of charge remained motionless, while the other type of charge flowed from one piece of foil to the other. He further suggested that an excess of what he called this “electrical fluid” be called “positive electricity” and the deficiency of it be called “negative electricity.” His suggestion, with some minor modifications, is the model we use today. (With the experiments that he was able to do, this was a pure guess; he had no way of actually determining the sign of the moving charge. Unfortunately, he guessed wrong; we now know that the charges that flow are the ones Franklin labeled negative, and the positive charges remain largely motionless. Fortunately, as we’ll see, it makes no practical or theoretical difference which choice we make, as long as we stay consistent with our choice.)

Let’s list the specific observations that we have of this electric force:

• The force acts without physical contact between the two objects.
• The force can be either attractive or repulsive: If two interacting objects carry the same sign of charge, the force is repulsive; if the charges are of opposite sign, the force is attractive. These interactions are referred to as electrostatic repulsion and electrostatic attraction, respectively.
• Not all objects are affected by this force.
• The magnitude of the force decreases (rapidly) with increasing separation distance between the objects.

To be more precise, we find experimentally that the magnitude of the force decreases as the square of the distance between the two interacting objects increases. Thus, for example, when the distance between two interacting objects is doubled, the force between them decreases to one fourth what it was in the original system. We can also observe that the surroundings of the charged objects affect the magnitude of the force. However, we will explore this issue in a later chapter.

Properties of Electric Charge

In addition to the existence of two types of charge, several other properties of charge have been discovered.

• Charge is quantized. This means that electric charge comes in discrete amounts, and there is a smallest possible amount of charge that an object can have. In the SI system, this smallest amount is [latex]e\equiv 1.602\phantom{\rule{0.2em}{0ex}}×\phantom{\rule{0.2em}{0ex}}{10}^{-19}\phantom{\rule{0.2em}{0ex}}\text{C}[/latex]. No free particle can have less charge than this, and, therefore, the charge on any object—the charge on all objects—must be an integer multiple of this amount. All macroscopic, charged objects have charge because electrons have either been added or taken away from them, resulting in a net charge.
• The magnitude of the charge is independent of the type. Phrased another way, the smallest possible positive charge (to four significant figures) is [latex]\text{+}1.602\phantom{\rule{0.2em}{0ex}}×\phantom{\rule{0.2em}{0ex}}{10}^{-19}\phantom{\rule{0.2em}{0ex}}\text{C}[/latex], and the smallest possible negative charge is [latex]-1.602\phantom{\rule{0.2em}{0ex}}×\phantom{\rule{0.2em}{0ex}}{10}^{-19}\phantom{\rule{0.2em}{0ex}}\text{C}[/latex]; these values are exactly equal. This is simply how the laws of physics in our universe turned out.
• Charge is conserved. Charge can neither be created nor destroyed; it can only be transferred from place to place, from one object to another. Frequently, we speak of two charges “canceling”; this is verbal shorthand. It means that if two objects that have equal and opposite charges are physically close to each other, then the (oppositely directed) forces they apply on some other charged object cancel, for a net force of zero. It is important that you understand that the charges on the objects by no means disappear, however. The net charge of the universe is constant.
• Charge is conserved in closed systems. In principle, if a negative charge disappeared from your lab bench and reappeared on the Moon, conservation of charge would still hold. However, this never happens. If the total charge you have in your local system on your lab bench is changing, there will be a measurable flow of charge into or out of the system. Again, charges can and do move around, and their effects can and do cancel, but the net charge in your local environment (if closed) is conserved. The last two items are both referred to as the law of conservation of charge.

The Source of Charges: The Structure of the Atom

Once it became clear that all matter was composed of particles that came to be called atoms, it also quickly became clear that the constituents of the atom included both positively charged particles and negatively charged particles. The next question was, what are the physical properties of those electrically charged particles?

The negatively charged particle was the first one to be discovered. In 1897, the English physicist J. J. Thomson was studying what was then known as cathode rays. Some years before, the English physicist William Crookes had shown that these “rays” were negatively charged, but his experiments were unable to tell any more than that. (The fact that they carried a negative electric charge was strong evidence that these were not rays at all, but particles.) Thomson prepared a pure beam of these particles and sent them through crossed electric and magnetic fields, and adjusted the various field strengths until the net deflection of the beam was zero. With this experiment, he was able to determine the charge-to-mass ratio of the particle. This ratio showed that the mass of the particle was much smaller than that of any other previously known particle—1837 times smaller, in fact. Eventually, this particle came to be called the electron.

Since the atom as a whole is electrically neutral, the next question was to determine how the positive and negative charges are distributed within the atom. Thomson himself imagined that his electrons were embedded within a sort of positively charged paste, smeared out throughout the volume of the atom. However, in 1908, the New Zealand physicist Ernest Rutherford showed that the positive charges of the atom existed within a tiny core—called a nucleus—that took up only a very tiny fraction of the overall volume of the atom, but held over 99% of the mass. (See Linear Momentum and Collisions.) In addition, he showed that the negatively charged electrons perpetually orbited about this nucleus, forming a sort of electrically charged cloud that surrounds the nucleus (Figure 5.7). Rutherford concluded that the nucleus was constructed of small, massive particles that he named protons.

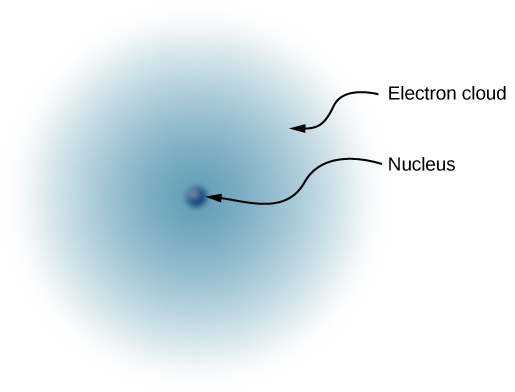
Since it was known that different atoms have different masses, and that ordinarily atoms are electrically neutral, it was natural to suppose that different atoms have different numbers of protons in their nucleus, with an equal number of negatively charged electrons orbiting about the positively charged nucleus, thus making the atoms overall electrically neutral. However, it was soon discovered that although the lightest atom, hydrogen, did indeed have a single proton as its nucleus, the next heaviest atom—helium—has twice the number of protons (two), but four times the mass of hydrogen.

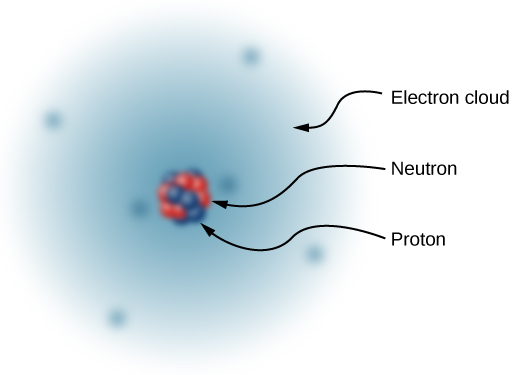
This mystery was resolved in 1932 by the English physicist James Chadwick, with the discovery of the neutron. The neutron is, essentially, an electrically neutral twin of the proton, with no electric charge, but (nearly) identical mass to the proton. The helium nucleus therefore has two neutrons along with its two protons. (Later experiments were to show that although the neutron is electrically neutral overall, it does have an internal charge structure. Furthermore, although the masses of the neutron and the proton are nearly equal, they aren’t exactly equal: The neutron’s mass is very slightly larger than the mass of the proton. That slight mass excess turned out to be of great importance. That, however, is a story that will have to wait until our study of modern physics in Nuclear Physics.)

Thus, in 1932, the picture of the atom was of a small, massive nucleus constructed of a combination of protons and neutrons, surrounded by a collection of electrons whose combined motion formed a sort of negatively charged “cloud” around the nucleus (Figure 5.8). In an electrically neutral atom, the total negative charge of the collection of electrons is equal to the total positive charge in the nucleus. The very low-mass electrons can be more or less easily removed or added to an atom, changing the net charge on the atom (though without changing its type). An atom that has had the charge altered in this way is called an ion. Positive ions have had electrons removed, whereas negative ions have had excess electrons added. We also use this term to describe molecules that are not electrically neutral.

The story of the atom does not stop there, however. In the latter part of the twentieth century, many more subatomic particles were discovered in the nucleus of the atom: pions, neutrinos, and quarks, among others. With the exception of the photon, none of these particles are directly relevant to the study of electromagnetism, so we defer further discussion of them until the chapter on particle physics (Particle Physics and Cosmology).

A Note on Terminology

As noted previously, electric charge is a property that an object can have. This is similar to how an object can have a property that we call mass, a property that we call density, a property that we call temperature, and so on. Technically, we should always say something like, “Suppose we have a particle that carries a charge of [latex]3\phantom{\rule{0.2em}{0ex}}\mu \text{C}.[/latex]” However, it is very common to say instead, “Suppose we have a [latex]3\text{-}\mu \text{C}[/latex] charge.” Similarly, we often say something like, “Six charges are located at the vertices of a regular hexagon.” A charge is not a particle; rather, it is a property of a particle. Nevertheless, this terminology is extremely common (and is frequently used in this book, as it is everywhere else). So, keep in the back of your mind what we really mean when we refer to a “charge.”