Chapter 10. Direct-Current Circuits
10.1 Electromotive Force
Learning Objectives
By the end of the section, you will be able to:
- Describe the electromotive force (emf) and the internal resistance of a battery
- Explain the basic operation of a battery
If you forget to turn off your car lights, they slowly dim as the battery runs down. Why don’t they suddenly blink off when the battery’s energy is gone? Their gradual dimming implies that the battery output voltage decreases as the battery is depleted. The reason for the decrease in output voltage for depleted batteries is that all voltage sources have two fundamental parts—a source of electrical energy and an internal resistance. In this section, we examine the energy source and the internal resistance.
Introduction to Electromotive Force
Voltage has many sources, a few of which are shown in Figure 10.2. All such devices create a potential difference and can supply current if connected to a circuit. A special type of potential difference is known as electromotive force (emf). The emf is not a force at all, but the term ‘electromotive force’ is used for historical reasons. It was coined by Alessandro Volta in the 1800s, when he invented the first battery, also known as the voltaic pile. Because the electromotive force is not a force, it is common to refer to these sources simply as sources of emf (pronounced as the letters “ee-em-eff”), instead of sources of electromotive force.

If the electromotive force is not a force at all, then what is the emf and what is a source of emf? To answer these questions, consider a simple circuit of a 12-V lamp attached to a 12-V battery, as shown in Figure 10.3. The battery can be modeled as a two-terminal device that keeps one terminal at a higher electric potential than the second terminal. The higher electric potential is sometimes called the positive terminal and is labeled with a plus sign. The lower-potential terminal is sometimes called the negative terminal and labeled with a minus sign. This is the source of the emf.
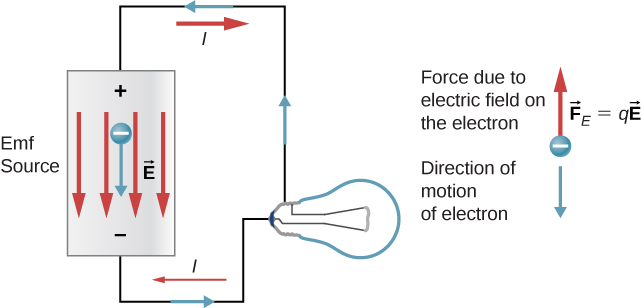
When the emf source is not connected to the lamp, there is no net flow of charge within the emf source. Once the battery is connected to the lamp, charges flow from one terminal of the battery, through the lamp (causing the lamp to light), and back to the other terminal of the battery. If we consider positive (conventional) current flow, positive charges leave the positive terminal, travel through the lamp, and enter the negative terminal.
Positive current flow is useful for most of the circuit analysis in this chapter, but in metallic wires and resistors, electrons contribute the most to current, flowing in the opposite direction of positive current flow. Therefore, it is more realistic to consider the movement of electrons for the analysis of the circuit in Figure 10.3. The electrons leave the negative terminal, travel through the lamp, and return to the positive terminal. In order for the emf source to maintain the potential difference between the two terminals, negative charges (electrons) must be moved from the positive terminal to the negative terminal. The emf source acts as a charge pump, moving negative charges from the positive terminal to the negative terminal to maintain the potential difference. This increases the potential energy of the charges and, therefore, the electric potential of the charges.
The force on the negative charge from the electric field is in the opposite direction of the electric field, as shown in Figure 10.3. In order for the negative charges to be moved to the negative terminal, work must be done on the negative charges. This requires energy, which comes from chemical reactions in the battery. The potential is kept high on the positive terminal and low on the negative terminal to maintain the potential difference between the two terminals. The emf is equal to the work done on the charge per unit charge [latex]\left(\epsilon =\frac{dW}{dq}\right)[/latex] when there is no current flowing. Since the unit for work is the joule and the unit for charge is the coulomb, the unit for emf is the volt [latex]\left(1\phantom{\rule{0.2em}{0ex}}\text{V}=1\phantom{\rule{0.2em}{0ex}}\text{J/C}\right).[/latex]
The terminal voltage [latex]{V}_{\text{terminal}}[/latex] of a battery is voltage measured across the terminals of the battery when there is no load connected to the terminal. An ideal battery is an emf source that maintains a constant terminal voltage, independent of the current between the two terminals. An ideal battery has no internal resistance, and the terminal voltage is equal to the emf of the battery. In the next section, we will show that a real battery does have internal resistance and the terminal voltage is always less than the emf of the battery.
The Origin of Battery Potential
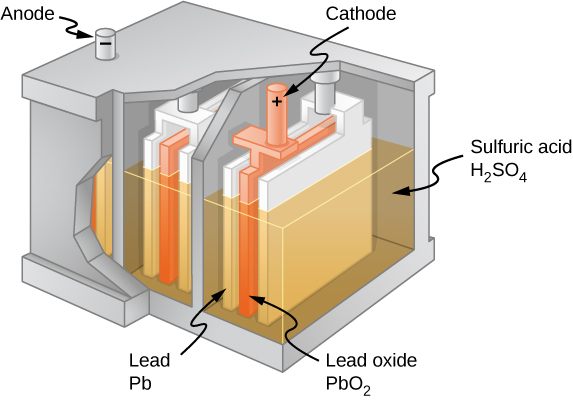
The combination of chemicals and the makeup of the terminals in a battery determine its emf. The lead acid battery used in cars and other vehicles is one of the most common combinations of chemicals. Figure 10.4 shows a single cell (one of six) of this battery. The cathode (positive) terminal of the cell is connected to a lead oxide plate, whereas the anode (negative) terminal is connected to a lead plate. Both plates are immersed in sulfuric acid, the electrolyte for the system.
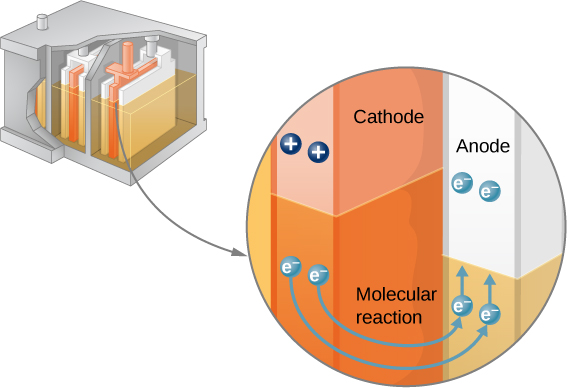
Knowing a little about how the chemicals in a lead-acid battery interact helps in understanding the potential created by the battery. Figure 10.5 shows the result of a single chemical reaction. Two electrons are placed on the anode, making it negative, provided that the cathode supplies two electrons. This leaves the cathode positively charged, because it has lost two electrons. In short, a separation of charge has been driven by a chemical reaction.
Note that the reaction does not take place unless there is a complete circuit to allow two electrons to be supplied to the cathode. Under many circumstances, these electrons come from the anode, flow through a resistance, and return to the cathode. Note also that since the chemical reactions involve substances with resistance, it is not possible to create the emf without an internal resistance.
Internal Resistance and Terminal Voltage
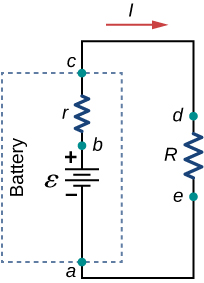
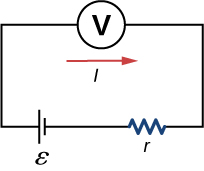
The amount of resistance to the flow of current within the voltage source is called the internal resistance. The internal resistance r of a battery can behave in complex ways. It generally increases as a battery is depleted, due to the oxidation of the plates or the reduction of the acidity of the electrolyte. However, internal resistance may also depend on the magnitude and direction of the current through a voltage source, its temperature, and even its history. The internal resistance of rechargeable nickel-cadmium cells, for example, depends on how many times and how deeply they have been depleted. A simple model for a battery consists of an idealized emf source [latex]\epsilon[/latex] and an internal resistance r (Figure 10.6).

Suppose an external resistor, known as the load resistance R, is connected to a voltage source such as a battery, as in Figure 10.7. The figure shows a model of a battery with an emf [latex]\epsilon[/latex], an internal resistance r, and a load resistor R connected across its terminals. Using conventional current flow, positive charges leave the positive terminal of the battery, travel through the resistor, and return to the negative terminal of the battery. The terminal voltage of the battery depends on the emf, the internal resistance, and the current, and is equal to
For a given emf and internal resistance, the terminal voltage decreases as the current increases due to the potential drop Ir of the internal resistance.
A graph of the potential difference across each element the circuit is shown in Figure 10.8. A current I runs through the circuit, and the potential drop across the internal resistor is equal to Ir. The terminal voltage is equal to [latex]\epsilon -Ir[/latex], which is equal to the potential drop across the load resistor [latex]IR=\epsilon -Ir[/latex]. As with potential energy, it is the change in voltage that is important. When the term “voltage” is used, we assume that it is actually the change in the potential, or [latex]\text{Δ}V[/latex]. However, [latex]\text{Δ}[/latex] is often omitted for convenience.
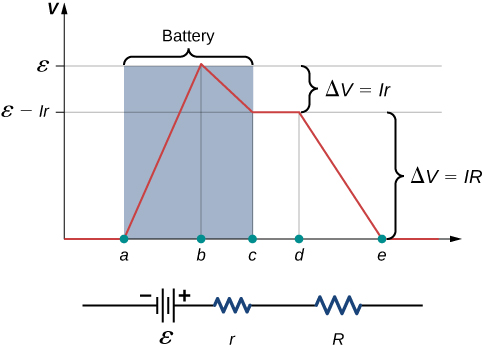
The current through the load resistor is [latex]I=\frac{\epsilon }{r+R}[/latex]. We see from this expression that the smaller the internal resistance r, the greater the current the voltage source supplies to its load R. As batteries are depleted, r increases. If r becomes a significant fraction of the load resistance, then the current is significantly reduced, as the following example illustrates.
Example
Analyzing a Circuit with a Battery and a Load
A given battery has a 12.00-V emf and an internal resistance of [latex]0.100\phantom{\rule{0.2em}{0ex}}\text{Ω}[/latex]. (a) Calculate its terminal voltage when connected to a [latex]10.00\text{-}\text{Ω}[/latex] load. (b) What is the terminal voltage when connected to a [latex]0.500\text{-}\text{Ω}[/latex] load? (c) What power does the [latex]0.500\text{-}\text{Ω}[/latex] load dissipate? (d) If the internal resistance grows to [latex]0.500\phantom{\rule{0.2em}{0ex}}\text{Ω}[/latex], find the current, terminal voltage, and power dissipated by a [latex]0.500\text{-}\text{Ω}[/latex] load.
Strategy
The analysis above gave an expression for current when internal resistance is taken into account. Once the current is found, the terminal voltage can be calculated by using the equation [latex]{V}_{\text{terminal}}=\epsilon -Ir[/latex]. Once current is found, we can also find the power dissipated by the resistor.
Solution
Show Answer
- Entering the given values for the emf, load resistance, and internal resistance into the expression above yields
[latex]I=\frac{\epsilon }{R+r}=\frac{12.00\phantom{\rule{0.2em}{0ex}}\text{V}}{10.10\phantom{\rule{0.2em}{0ex}}\text{Ω}}=1.188\phantom{\rule{0.2em}{0ex}}\text{A}.[/latex]
Enter the known values into the equation [latex]{V}_{\text{terminal}}=\epsilon -Ir[/latex] to get the terminal voltage:
[latex]{V}_{\text{terminal}}=\epsilon -Ir=12.00\phantom{\rule{0.2em}{0ex}}\text{V}\phantom{\rule{0.2em}{0ex}}-\left(1.188\phantom{\rule{0.2em}{0ex}}\text{A}\right)\left(0.100\phantom{\rule{0.2em}{0ex}}\text{Ω}\right)=11.90\phantom{\rule{0.2em}{0ex}}\text{V}.[/latex]
The terminal voltage here is only slightly lower than the emf, implying that the current drawn by this light load is not significant. - Similarly, with [latex]{R}_{\text{load}}=0.500\phantom{\rule{0.2em}{0ex}}\text{Ω}[/latex], the current is
[latex]I=\frac{\epsilon }{R+r}=\frac{12.00\phantom{\rule{0.2em}{0ex}}\text{V}}{0.600\phantom{\rule{0.2em}{0ex}}\text{Ω}}=20.00\phantom{\rule{0.2em}{0ex}}\text{A}.[/latex]
The terminal voltage is now
[latex]{V}_{\text{terminal}}=\epsilon -Ir=12.00\phantom{\rule{0.2em}{0ex}}\text{V}-\left(20.00\phantom{\rule{0.2em}{0ex}}\text{A}\right)\left(0.100\phantom{\rule{0.2em}{0ex}}\text{Ω}\right)=10.00\phantom{\rule{0.2em}{0ex}}\text{V}.[/latex]
The terminal voltage exhibits a more significant reduction compared with emf, implying [latex]0.500\phantom{\rule{0.2em}{0ex}}\text{Ω}[/latex] is a heavy load for this battery. A “heavy load” signifies a larger draw of current from the source but not a larger resistance. - The power dissipated by the [latex]0.500\text{-}\text{Ω}[/latex] load can be found using the formula [latex]P={I}^{2}R[/latex]. Entering the known values gives
[latex]P={I}^{2}R={\left(20.0\phantom{\rule{0.2em}{0ex}}\text{A}\right)}^{2}\left(0.500\phantom{\rule{0.2em}{0ex}}\text{Ω}\right)=2.00\phantom{\rule{0.2em}{0ex}}×\phantom{\rule{0.2em}{0ex}}{10}^{2}\phantom{\rule{0.2em}{0ex}}\text{W.}[/latex]
Note that this power can also be obtained using the expression [latex]\frac{{V}^{2}}{R}\phantom{\rule{0.2em}{0ex}}\text{or}\phantom{\rule{0.2em}{0ex}}IV[/latex], where V is the terminal voltage (10.0 V in this case). - Here, the internal resistance has increased, perhaps due to the depletion of the battery, to the point where it is as great as the load resistance. As before, we first find the current by entering the known values into the expression, yielding
[latex]I=\frac{\epsilon }{R+r}=\frac{12.00\phantom{\rule{0.2em}{0ex}}\text{V}}{1.00\phantom{\rule{0.2em}{0ex}}\text{Ω}}=12.00\phantom{\rule{0.2em}{0ex}}\text{A}.[/latex]
Now the terminal voltage is
[latex]{V}_{\text{terminal}}=\epsilon -Ir=12.00\phantom{\rule{0.2em}{0ex}}\text{V}-\left(12.00\phantom{\rule{0.2em}{0ex}}\text{A}\right)\left(0.500\phantom{\rule{0.2em}{0ex}}\text{Ω}\right)=6.00\phantom{\rule{0.2em}{0ex}}\text{V},[/latex]
and the power dissipated by the load is
[latex]P={I}^{2}R={\left(12.00\phantom{\rule{0.2em}{0ex}}\text{A}\right)}^{2}\left(0.500\phantom{\rule{0.2em}{0ex}}\text{Ω}\right)=72.00\phantom{\rule{0.2em}{0ex}}\text{W.}[/latex]
We see that the increased internal resistance has significantly decreased the terminal voltage, current, and power delivered to a load.
Significance
The internal resistance of a battery can increase for many reasons. For example, the internal resistance of a rechargeable battery increases as the number of times the battery is recharged increases. The increased internal resistance may have two effects on the battery. First, the terminal voltage will decrease. Second, the battery may overheat due to the increased power dissipated by the internal resistance.
Check Your Understanding
If you place a wire directly across the two terminal of a battery, effectively shorting out the terminals, the battery will begin to get hot. Why do you suppose this happens?
Show Solution
If a wire is connected across the terminals, the load resistance is close to zero, or at least considerably less than the internal resistance of the battery. Since the internal resistance is small, the current through the circuit will be large, [latex]I=\frac{\epsilon }{R+r}=\frac{\epsilon }{0+r}=\frac{\epsilon }{r}.[/latex] The large current causes a high power to be dissipated by the internal resistance [latex]\left(P={I}^{2}r\right)[/latex]. The power is dissipated as heat.
Battery Testers
Battery testers, such as those in Figure 10.9, use small load resistors to intentionally draw current to determine whether the terminal potential drops below an acceptable level. Although it is difficult to measure the internal resistance of a battery, battery testers can provide a measurement of the internal resistance of the battery. If internal resistance is high, the battery is weak, as evidenced by its low terminal voltage.

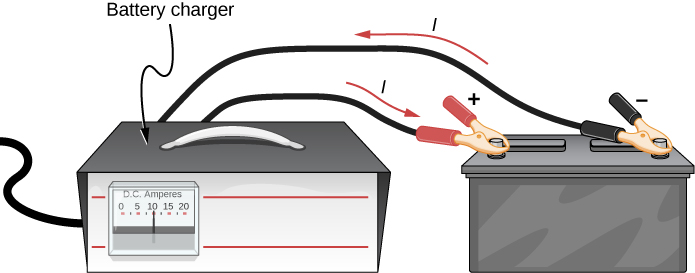
Some batteries can be recharged by passing a current through them in the direction opposite to the current they supply to an appliance. This is done routinely in cars and in batteries for small electrical appliances and electronic devices (Figure 10.10). The voltage output of the battery charger must be greater than the emf of the battery to reverse the current through it. This causes the terminal voltage of the battery to be greater than the emf, since [latex]V=\epsilon -Ir[/latex] and I is now negative.
It is important to understand the consequences of the internal resistance of emf sources, such as batteries and solar cells, but often, the analysis of circuits is done with the terminal voltage of the battery, as we have done in the previous sections. The terminal voltage is referred to as simply as V, dropping the subscript “terminal.” This is because the internal resistance of the battery is difficult to measure directly and can change over time.
Summary
- All voltage sources have two fundamental parts: a source of electrical energy that has a characteristic electromotive force (emf), and an internal resistance r. The emf is the work done per charge to keep the potential difference of a source constant. The emf is equal to the potential difference across the terminals when no current is flowing. The internal resistance r of a voltage source affects the output voltage when a current flows.
- The voltage output of a device is called its terminal voltage [latex]{V}_{\text{terminal}}[/latex] and is given by [latex]{V}_{\text{terminal}}=\epsilon -Ir[/latex], where I is the electric current and is positive when flowing away from the positive terminal of the voltage source and r is the internal resistance.
Conceptual Questions
What effect will the internal resistance of a rechargeable battery have on the energy being used to recharge the battery?
Show Solution
Some of the energy being used to recharge the battery will be dissipated as heat by the internal resistance.
A battery with an internal resistance of r and an emf of 10.00 V is connected to a load resistor [latex]R=r[/latex]. As the battery ages, the internal resistance triples. How much is the current through the load resistor reduced?
Show that the power dissipated by the load resistor is maximum when the resistance of the load resistor is equal to the internal resistance of the battery.
Show Solution
[latex]\begin{array}{}\\ \\ P={I}^{2}R={\left(\frac{\epsilon }{r+R}\right)}^{2}R={\epsilon }^{2}R{\left(r+R\right)}^{-2},\phantom{\rule{0.5em}{0ex}}\frac{dP}{dR}={\epsilon }^{2}\left[{\left(r+R\right)}^{-2}-2R{\left(r+R\right)}^{-3}\right]=0,\hfill \\ \left[\frac{\left(r+R\right)-2R}{{\left(r+R\right)}^{3}}\right]=0,\phantom{\rule{0.5em}{0ex}}r=R\hfill \end{array}[/latex]
Problems
A car battery with a 12-V emf and an internal resistance of [latex]0.050\phantom{\rule{0.2em}{0ex}}\text{Ω}[/latex] is being charged with a current of 60 A. Note that in this process, the battery is being charged. (a) What is the potential difference across its terminals? (b) At what rate is thermal energy being dissipated in the battery? (c) At what rate is electric energy being converted into chemical energy?
The label on a battery-powered radio recommends the use of a rechargeable nickel-cadmium cell (nicads), although it has a 1.25-V emf, whereas an alkaline cell has a 1.58-V emf. The radio has a [latex]3.20\phantom{\rule{0.2em}{0ex}}\text{Ω}[/latex] resistance. (a) Draw a circuit diagram of the radio and its battery. Now, calculate the power delivered to the radio (b) when using a nicad cells, each having an internal resistance of [latex]0.0400\phantom{\rule{0.2em}{0ex}}\text{Ω}[/latex], and (c) when using an alkaline cell, having an internal resistance of [latex]0.200\phantom{\rule{0.2em}{0ex}}\text{Ω}[/latex]. (d) Does this difference seem significant, considering that the radio’s effective resistance is lowered when its volume is turned up?
Show Solution
a.
b. 0.476W; c. 0.691 W; d. As [latex]{R}_{L}[/latex] is lowered, the power difference decreases; therefore, at higher volumes, there is no significant difference.
An automobile starter motor has an equivalent resistance of [latex]0.0500\phantom{\rule{0.2em}{0ex}}\text{Ω}[/latex] and is supplied by a 12.0-V battery with a [latex]0.0100\text{-}\text{Ω}[/latex] internal resistance. (a) What is the current to the motor? (b) What voltage is applied to it? (c) What power is supplied to the motor? (d) Repeat these calculations for when the battery connections are corroded and add [latex]0.0900\phantom{\rule{0.2em}{0ex}}\text{Ω}[/latex] to the circuit. (Significant problems are caused by even small amounts of unwanted resistance in low-voltage, high-current applications.)
(a) What is the internal resistance of a voltage source if its terminal potential drops by 2.00 V when the current supplied increases by 5.00 A? (b) Can the emf of the voltage source be found with the information supplied?
Show Solution
a. [latex]0.400\phantom{\rule{0.2em}{0ex}}\text{Ω}[/latex]; b. No, there is only one independent equation, so only r can be found.
A person with body resistance between his hands of [latex]10.0\phantom{\rule{0.2em}{0ex}}\text{k}\text{Ω}[/latex] accidentally grasps the terminals of a 20.0-kV power supply. (Do NOT do this!) (a) Draw a circuit diagram to represent the situation. (b) If the internal resistance of the power supply is [latex]2000\phantom{\rule{0.2em}{0ex}}\text{Ω}[/latex], what is the current through his body? (c) What is the power dissipated in his body? (d) If the power supply is to be made safe by increasing its internal resistance, what should the internal resistance be for the maximum current in this situation to be 1.00 mA or less? (e) Will this modification compromise the effectiveness of the power supply for driving low-resistance devices? Explain your reasoning.
A 12.0-V emf automobile battery has a terminal voltage of 16.0 V when being charged by a current of 10.0 A. (a) What is the battery’s internal resistance? (b) What power is dissipated inside the battery? (c) At what rate (in [latex]\text{°}\text{C}\text{/}\text{min}[/latex]) will its temperature increase if its mass is 20.0 kg and it has a specific heat of [latex]0.300\phantom{\rule{0.2em}{0ex}}\text{kcal/kg}\phantom{\rule{0.2em}{0ex}}·\text{°}\text{C}[/latex], assuming no heat escapes?
Show Solution
a. [latex]0.400\phantom{\rule{0.2em}{0ex}}\text{Ω}[/latex]; b. 40.0 W; c. [latex]0.0956\phantom{\rule{0.2em}{0ex}}\text{°C/min}[/latex]
Glossary
- electromotive force (emf)
- energy produced per unit charge, drawn from a source that produces an electrical current
- internal resistance
- amount of resistance to the flow of current within the voltage source
- potential difference
- difference in electric potential between two points in an electric circuit, measured in volts
- potential drop
- loss of electric potential energy as a current travels across a resistor, wire, or other component
- terminal voltage
- potential difference measured across the terminals of a source when there is no load attached
Licenses and Attributions
Electromotive Force. Authored by: OpenStax College. Located at: https://openstax.org/books/university-physics-volume-2/pages/10-1-electromotive-force. License: CC BY: Attribution. License Terms: Download for free at https://openstax.org/books/university-physics-volume-2/pages/1-introduction

