Chapter 14. Inductance
14.3 Energy in a Magnetic Field
Learning Objectives
By the end of this section, you will be able to:
- Explain how energy can be stored in a magnetic field
- Derive the equation for energy stored in a coaxial cable given the magnetic energy density
The energy of a capacitor is stored in the electric field between its plates. Similarly, an inductor has the capability to store energy, but in its magnetic field. This energy can be found by integrating the magnetic energy density,
over the appropriate volume. To understand where this formula comes from, let’s consider the long, cylindrical solenoid of the previous section. Again using the infinite solenoid approximation, we can assume that the magnetic field is essentially constant and given by [latex]B={\mu }_{0}nI[/latex] everywhere inside the solenoid. Thus, the energy stored in a solenoid or the magnetic energy density times volume is equivalent to
With the substitution of Equation 14.14, this becomes
Although derived for a special case, this equation gives the energy stored in the magnetic field of any inductor. We can see this by considering an arbitrary inductor through which a changing current is passing. At any instant, the magnitude of the induced emf is [latex]\epsilon =Ldi\text{/}dt,[/latex] so the power absorbed by the inductor is
The total energy stored in the magnetic field when the current increases from 0 to I in a time interval from 0 to t can be determined by integrating this expression:
Example
Self-Inductance of a Coaxial Cable
Equation 14.11 shows two long, concentric cylindrical shells of radii [latex]{R}_{1}[/latex] and [latex]{R}_{2}.[/latex] As discussed in Capacitance on capacitance, this configuration is a simplified representation of a coaxial cable. The capacitance per unit length of the cable has already been calculated. Now (a) determine the magnetic energy stored per unit length of the coaxial cable and (b) use this result to find the self-inductance per unit length of the cable.
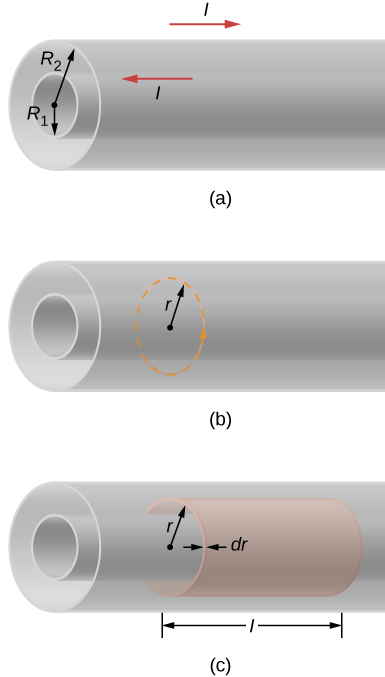
Strategy
The magnetic field both inside and outside the coaxial cable is determined by Ampère’s law. Based on this magnetic field, we can use Equation 14.22 to calculate the energy density of the magnetic field. The magnetic energy is calculated by an integral of the magnetic energy density times the differential volume over the cylindrical shell. After the integration is carried out, we have a closed-form solution for part (a). The self-inductance per unit length is determined based on this result and Equation 14.22.
Solution
Show Answer
- We determine the magnetic field between the conductors by applying Ampère’s law to the dashed circular path shown in Figure 14.11(b). Because of the cylindrical symmetry, [latex]\stackrel{\to }{\textbf{B}}[/latex] is constant along the path, and
[latex]\oint \stackrel{\to }{\textbf{B}}·d\stackrel{\to }{\textbf{l}}=B\left(2\pi r\right)={\mu }_{0}I.[/latex]
This gives us
[latex]B=\frac{{\mu }_{0}I}{2\pi r}.[/latex]
In the region outside the cable, a similar application of Ampère’s law shows that [latex]B=0[/latex], since no net current crosses the area bounded by a circular path where [latex]r > {R}_{2}.[/latex] This argument also holds when [latex]r < {R}_{1};[/latex] that is, in the region within the inner cylinder. All the magnetic energy of the cable is therefore stored between the two conductors. Since the energy density of the magnetic field is
[latex]{u}_{\text{m}}=\frac{{B}^{2}}{2{\mu }_{0}}=\frac{{\mu }_{0}{I}^{2}}{8{\pi }^{2}{r}^{2}},[/latex]
the energy stored in a cylindrical shell of inner radius r, outer radius [latex]r+dr,[/latex] and length l (see part (c) of the figure) is
[latex]{u}_{\text{m}}=\frac{{B}^{2}}{2{\mu }_{0}}=\frac{{\mu }_{0}{I}^{2}}{8{\pi }^{2}{r}^{2}}.[/latex]
Thus, the total energy of the magnetic field in a length l of the cable is
[latex]U={\int }_{{R}_{1}}^{{R}_{2}}dU={\int }_{{R}_{1}}^{{R}_{2}}\frac{{\mu }_{0}{I}^{2}}{8{\pi }^{2}{r}^{2}}\left(2\pi rl\right)dr=\frac{{\mu }_{0}{I}^{2}l}{4\pi }\phantom{\rule{0.2em}{0ex}}\text{ln}\phantom{\rule{0.2em}{0ex}}\frac{{R}_{2}}{{R}_{1}},[/latex]
and the energy per unit length is [latex]\left({\mu }_{0}{I}^{2}\text{/}4\pi \right)\text{ln}\left({R}_{2}\text{/}{R}_{1}\right)[/latex]. - From Figure 14.22,
[latex]U=\frac{1}{2}L{I}^{2},[/latex]
where L is the self-inductance of a length l of the coaxial cable. Equating the previous two equations, we find that the self-inductance per unit length of the cable is
[latex]\frac{L}{l}=\frac{{\mu }_{0}}{2\pi }\phantom{\rule{0.2em}{0ex}}\text{ln}\phantom{\rule{0.2em}{0ex}}\frac{{R}_{2}}{{R}_{1}}.[/latex]
Significance
The inductance per unit length depends only on the inner and outer radii as seen in the result. To increase the inductance, we could either increase the outer radius [latex]\left({R}_{2}\right)[/latex] or decrease the inner radius [latex]\left({R}_{1}\right)[/latex]. In the limit as the two radii become equal, the inductance goes to zero. In this limit, there is no coaxial cable. Also, the magnetic energy per unit length from part (a) is proportional to the square of the current.
Check Your Understanding
How much energy is stored in the inductor of Example 14.2 after the current reaches its maximum value?
Show Solution
0.50 J
Summary
- The energy stored in an inductor U is
[latex]U=\frac{1}{2}L{I}^{2}.[/latex] - The self-inductance per unit length of coaxial cable is
[latex]\frac{L}{l}=\frac{{\mu }_{0}}{2\pi }\phantom{\rule{0.2em}{0ex}}\text{ln}\phantom{\rule{0.2em}{0ex}}\frac{{R}_{2}}{{R}_{1}}.[/latex]
Conceptual Questions
Show that [latex]L{I}^{2}\text{/}2[/latex] has units of energy.
Problems
At the instant a current of 0.20 A is flowing through a coil of wire, the energy stored in its magnetic field is [latex]6.0\phantom{\rule{0.2em}{0ex}}×\phantom{\rule{0.2em}{0ex}}{10}^{-3}\phantom{\rule{0.2em}{0ex}}\text{J}.[/latex] What is the self-inductance of the coil?
Suppose that a rectangular toroid has 2000 windings and a self-inductance of 0.040 H. If [latex]h=0.10\phantom{\rule{0.2em}{0ex}}\text{m}[/latex], what is the current flowing through a rectangular toroid when the energy in its magnetic field is [latex]2.0\phantom{\rule{0.2em}{0ex}}×\phantom{\rule{0.2em}{0ex}}{10}^{-6}\phantom{\rule{0.2em}{0ex}}\text{J}?[/latex]
Show Solution
0.01 A
Solenoid A is tightly wound while solenoid B has windings that are evenly spaced with a gap equal to the diameter of the wire. The solenoids are otherwise identical. Determine the ratio of the energies stored per unit length of these solenoids when the same current flows through each.
A 10-H inductor carries a current of 20 A. How much ice at [latex]0\text{°}\phantom{\rule{0.2em}{0ex}}\text{C}[/latex] could be melted by the energy stored in the magnetic field of the inductor? (Hint: Use the value [latex]{L}_{\text{f}}=334\phantom{\rule{0.2em}{0ex}}\text{J/g}[/latex] for ice.)
Show Solution
6.0 g
A coil with a self-inductance of 3.0 H and a resistance of [latex]100\phantom{\rule{0.2em}{0ex}}\text{Ω}[/latex] carries a steady current of 2.0 A. (a) What is the energy stored in the magnetic field of the coil? (b) What is the energy per second dissipated in the resistance of the coil?
A current of 1.2 A is flowing in a coaxial cable whose outer radius is five times its inner radius. What is the magnetic field energy stored in a 3.0-m length of the cable?
Show Solution
[latex]{U}_{\text{m}}=7.0\phantom{\rule{0.2em}{0ex}}×\phantom{\rule{0.2em}{0ex}}{10}^{-7}\phantom{\rule{0.2em}{0ex}}\text{J}[/latex]
Glossary
- magnetic energy density
- energy stored per volume in a magnetic field
Licenses and Attributions
Energy in a Magnetic Field. Authored by: OpenStax College. Located at: https://openstax.org/books/university-physics-volume-2/pages/14-3-energy-in-a-magnetic-field. License: CC BY: Attribution. License Terms: Download for free at https://openstax.org/books/university-physics-volume-2/pages/1-introduction

