Chapter 14. Inductance

14.6 RLC Series Circuits

Learning Objectives

By the end of this section, you will be able to:

  • Determine the angular frequency of oscillation for a resistor, inductor, capacitor [latex]\left(RLC\right)[/latex] series circuit
  • Relate the [latex]RLC[/latex] circuit to a damped spring oscillation

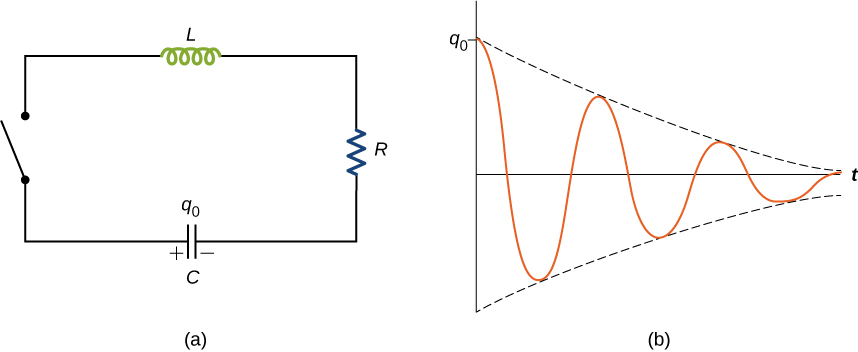
When the switch is closed in the RLC circuit of Figure 14.17(a), the capacitor begins to discharge and electromagnetic energy is dissipated by the resistor at a rate [latex]{i}^{2}R[/latex]. With U given by Equation 14.19, we have

[latex]\frac{dU}{dt}=\frac{q}{C}\phantom{\rule{0.2em}{0ex}}\frac{dq}{dt}+Li\frac{di}{dt}=\text{−}{i}^{2}R[/latex]

where i and q are time-dependent functions. This reduces to

[latex]L\frac{{d}^{2}q}{d{t}^{2}}+R\frac{dq}{dt}+\frac{1}{C}q=0.[/latex]
Figure a is a circuit with a capacitor, an inductor and a resistor in series with each other. They are also in series with a switch, which is open. Figure b shows the graph of charge versus time. The charge is at maximum value, q0, at t=0. The curve is similar to a sine wave that reduces in amplitude till it becomes zero.
Figure 14.17 (a) An RLC circuit. Electromagnetic oscillations begin when the switch is closed. The capacitor is fully charged initially. (b) Damped oscillations of the capacitor charge are shown in this curve of charge versus time, or q versus t. The capacitor contains a charge [latex]{q}_{0}[/latex] before the switch is closed.

This equation is analogous to

[latex]m\frac{{d}^{2}x}{d{t}^{2}}+b\frac{dx}{dt}+kx=0,[/latex]

which is the equation of motion for a damped mass-spring system (you first encountered this equation in Oscillations). As we saw in that chapter, it can be shown that the solution to this differential equation takes three forms, depending on whether the angular frequency of the undamped spring is greater than, equal to, or less than b/2m. Therefore, the result can be underdamped [latex]\left(\sqrt{k\text{/}m} > b\text{/}2m\right)[/latex], critically damped [latex]\left(\sqrt{k\text{/}m}=b\text{/}2m\right)[/latex], or overdamped [latex]\left(\sqrt{k\text{/}m} < b\text{/}2m\right)[/latex]. By analogy, the solution q(t) to the RLC differential equation has the same feature. Here we look only at the case of under-damping. By replacing m by L, b by R, k by 1/C, and x by q in Equation 14.44, and assuming [latex]\sqrt{1\text{/}LC}>R\text{/}2L[/latex], we obtain

[latex]q\left(t\right)={q}_{0}{e}^{\text{−}Rt\text{/}2L}\phantom{\rule{0.2em}{0ex}}\text{cos}\left(\omega \text{′}t+\varphi \right)[/latex]

where the angular frequency of the oscillations is given by

[latex]{\omega }^{\prime }=\sqrt{\frac{1}{LC}-{\left(\frac{R}{2L}\right)}^{2}}[/latex]

This underdamped solution is shown in Equation 14.17(b). Notice that the amplitude of the oscillations decreases as energy is dissipated in the resistor. Equation 14.45 can be confirmed experimentally by measuring the voltage across the capacitor as a function of time. This voltage, multiplied by the capacitance of the capacitor, then gives q(t).

Try an interactive circuit construction kit that allows you to graph current and voltage as a function of time. You can add inductors and capacitors to work with any combination of R, L, and C circuits with both dc and ac sources.

Try out a circuit-based java applet website that has many problems with both dc and ac sources that will help you practice circuit problems.

Check Your Understanding

In an RLC circuit, [latex]L=5.0\phantom{\rule{0.2em}{0ex}}\text{mH},C=6.0\mu \text{F},\phantom{\rule{0.2em}{0ex}}\text{and}\phantom{\rule{0.2em}{0ex}}R=200\phantom{\rule{0.2em}{0ex}}\text{Ω}.[/latex] (a) Is the circuit underdamped, critically damped, or overdamped? (b) If the circuit starts oscillating with a charge of [latex]3.0\phantom{\rule{0.2em}{0ex}}×\phantom{\rule{0.2em}{0ex}}{10}^{-3}\phantom{\rule{0.2em}{0ex}}\text{C}[/latex] on the capacitor, how much energy has been dissipated in the resistor by the time the oscillations cease?

Show Solution

a. overdamped; b. 0.75 J

Summary

  • The underdamped solution for the capacitor charge in an RLC circuit is

    [latex]q\left(t\right)={q}_{0}{e}^{\text{−}Rt\text{/}2L}\phantom{\rule{0.2em}{0ex}}\text{cos}\left(\omega \text{′}t+\varphi \right).[/latex]
  • The angular frequency given in the underdamped solution for the RLC circuit is

    [latex]{\omega }^{\prime }=\sqrt{\frac{1}{LC}-{\left(\frac{R}{2L}\right)}^{2}}.[/latex]

Key Equations

Mutual inductance by flux [latex]M=\frac{{N}_{2}{\text{Φ}}_{21}}{{I}_{1}}=\frac{{N}_{1}{\text{Φ}}_{12}}{{I}_{2}}[/latex]
Mutual inductance in circuits [latex]{\epsilon }_{1}=\text{−}M\frac{d{I}_{2}}{dt}[/latex]
Self-inductance in terms of magnetic flux [latex]N{\text{Φ}}_{\text{m}}=LI[/latex]
Self-inductance in terms of emf [latex]\epsilon =\text{−}L\frac{dI}{dt}[/latex]
Self-inductance of a solenoid [latex]{L}_{\text{solenoid}}=\frac{{\mu }_{0}{N}^{2}A}{l}[/latex]
Self-inductance of a toroid [latex]{L}_{\text{toroid}}=\frac{{\mu }_{0}{N}^{2}h}{2\pi }\phantom{\rule{0.2em}{0ex}}\text{ln}\phantom{\rule{0.2em}{0ex}}\frac{{R}_{2}}{{R}_{1}}.[/latex]
Energy stored in an inductor [latex]U=\frac{1}{2}L{I}^{2}[/latex]
Current as a function of time for a RL circuit [latex]I\left(t\right)=\frac{\text{ε}}{R}\left(1-{e}^{\text{−}t\text{/}{\tau }_{L}}\right)[/latex]
Time constant for a RL circuit [latex]{\tau }_{L}=L\text{/}R[/latex]
Charge oscillation in LC circuits [latex]q\left(t\right)={q}_{0}\phantom{\rule{0.2em}{0ex}}\text{cos}\left(\omega t+\varphi \right)[/latex]
Angular frequency in LC circuits [latex]\omega =\sqrt{\frac{1}{LC}}[/latex]
Current oscillations in LC circuits [latex]i\left(t\right)=\text{−}\omega {q}_{0}\phantom{\rule{0.2em}{0ex}}\text{sin}\left(\omega t+\varphi \right)[/latex]
Charge as a function of time in RLC circuit [latex]q\left(t\right)={q}_{0}{e}^{\text{−}Rt\text{/}2L}\phantom{\rule{0.2em}{0ex}}\text{cos}\left(\omega \text{′}t+\varphi \right)[/latex]
Angular frequency in RLC circuit [latex]\omega \text{′}=\sqrt{\frac{1}{LC}-{\left(\frac{R}{2L}\right)}^{2}}[/latex]

Conceptual Questions

When a wire is connected between the two ends of a solenoid, the resulting circuit can oscillate like an RLC circuit. Describe what causes the capacitance in this circuit.

Describe what effect the resistance of the connecting wires has on an oscillating LC circuit.

Show Solution

This creates an RLC circuit that dissipates energy, causing oscillations to decrease in amplitude slowly or quickly depending on the value of resistance.

Suppose you wanted to design an LC circuit with a frequency of 0.01 Hz. What problems might you encounter?

A radio receiver uses an RLC circuit to pick out particular frequencies to listen to in your house or car without hearing other unwanted frequencies. How would someone design such a circuit?

Show Solution

You would have to pick out a resistance that is small enough so that only one station at a time is picked up, but big enough so that the tuner doesn’t have to be set at exactly the correct frequency. The inductance or capacitance would have to be varied to tune into the station however practically speaking, variable capacitors are a lot easier to build in a circuit.

Problems

In an oscillating RLC circuit, [latex]R=5.0\phantom{\rule{0.2em}{0ex}}\text{Ω},L=5.0\phantom{\rule{0.2em}{0ex}}\text{mH},\phantom{\rule{0.2em}{0ex}}\text{and}\phantom{\rule{0.2em}{0ex}}C=500\phantom{\rule{0.2em}{0ex}}\mu \text{F}.[/latex] What is the angular frequency of the oscillations?

In an oscillating RLC circuit with [latex]L=10\phantom{\rule{0.2em}{0ex}}\text{mH},C=1.5\phantom{\rule{0.2em}{0ex}}µ\text{F},\phantom{\rule{0.2em}{0ex}}\text{and}\phantom{\rule{0.2em}{0ex}}R=2.0\phantom{\rule{0.2em}{0ex}}\text{Ω},[/latex] how much time elapses before the amplitude of the oscillations drops to half its initial value?

Show Solution

6.9 ms

What resistance R must be connected in series with a 200-mH inductor of the resulting RLC oscillating circuit is to decay to [latex]50\text{%}[/latex] of its initial value of charge in 50 cycles? To [latex]0.10\text{%}[/latex] of its initial value in 50 cycles?

Additional Problems

Show that the self-inductance per unit length of an infinite, straight, thin wire is infinite.

Show Solution

Let a equal the radius of the long, thin wire, r the location where the magnetic field is measured, and R the upper limit of the problem where we will take R as it approaches infinity.
proof [latex]\begin{array}{ccc}\hfill \text{Outside,}\phantom{\rule{1em}{0ex}}B& =\hfill & \frac{{\mu }_{0}I}{2\pi r}\phantom{\rule{0.5em}{0ex}}\text{Inside,}\phantom{\rule{1em}{0ex}}B=\frac{{\mu }_{0}Ir}{2\pi {a}^{2}}\hfill \\ \hfill U& =\hfill & \frac{{\mu }_{0}{I}^{2}l}{4\pi }\left(\frac{1}{4}+\text{ln}\phantom{\rule{0.2em}{0ex}}\frac{R}{a}\right)\hfill \\ \hfill \text{So,}\phantom{\rule{2em}{0ex}}\frac{2U}{{I}^{2}}& =\hfill & \frac{{\mu }_{0}l}{2\pi }\left(\frac{1}{4}+\text{ln}\phantom{\rule{0.2em}{0ex}}\frac{R}{a}\right)\phantom{\rule{0.5em}{0ex}}\text{and}\phantom{\rule{1em}{0ex}}L=\infty \hfill \end{array}[/latex]

Two long, parallel wires carry equal currents in opposite directions. The radius of each wire is a, and the distance between the centers of the wires is d. Show that if the magnetic flux within the wires themselves can be ignored, the self-inductance of a length l of such a pair of wires is

[latex]L=\frac{{\mu }_{0}l}{\pi }\phantom{\rule{0.2em}{0ex}}\text{ln}\phantom{\rule{0.2em}{0ex}}\frac{d-a}{a}.[/latex]

(Hint: Calculate the magnetic flux through a rectangle of length l between the wires and then use [latex]L=N\text{Φ}\text{/}I[/latex].)

A small, rectangular single loop of wire with dimensions l, and a is placed, as shown below, in the plane of a much larger, rectangular single loop of wire. The two short sides of the larger loop are so far from the smaller loop that their magnetic fields over the smaller fields over the smaller loop can be ignored. What is the mutual inductance of the two loops?

The figure shows a rectangular loop of wire. The length of the rectangle is l and width is a. On both sides of the rectangle are wires parallel to its length. They are a distance d away from the rectangle. Current I1 flows through both in opposites directions.

Show Solution

[latex]M=\frac{{\mu }_{0}l}{\pi }\phantom{\rule{0.2em}{0ex}}\text{ln}\phantom{\rule{0.2em}{0ex}}\frac{d+a}{d}[/latex]

Suppose that a cylindrical solenoid is wrapped around a core of iron whose magnetic susceptibility is x. Using Equation 14.9, show that the self-inductance of the solenoid is given by

[latex]L=\frac{\left(1+x\right){\mu }_{0}{N}^{2}A}{l},[/latex]

where l is its length, A its cross-sectional area, and N its total number of turns.

A solenoid with [latex]4x{10}^{7}[/latex] turns/m has an iron core placed in it whose magnetic susceptibility is [latex]4.0\phantom{\rule{0.2em}{0ex}}×\phantom{\rule{0.2em}{0ex}}{10}^{3}[/latex]. (a) If a current of 2.0 A flows through the solenoid, what is the magnetic field in the iron core? (b) What is the effective surface current formed by the aligned atomic current loops in the iron core? (c) What is the self-inductance of the filled solenoid?

Show Solution

a. 100 T; b. 2 A; c. 0.50 H

A rectangular toroid with inner radius [latex]{R}_{1}=7.0\phantom{\rule{0.2em}{0ex}}\text{cm,}[/latex] outer radius [latex]{R}_{2}=9.0\phantom{\rule{0.2em}{0ex}}\text{cm}[/latex], height [latex]h=3.0[/latex], and [latex]N=3000[/latex] turns is filled with an iron core of magnetic susceptibility [latex]5.2\phantom{\rule{0.2em}{0ex}}×\phantom{\rule{0.2em}{0ex}}{10}^{3}[/latex]. (a) What is the self-inductance of the toroid? (b) If the current through the toroid is 2.0 A, what is the magnetic field at the center of the core? (c) For this same 2.0-A current, what is the effective surface current formed by the aligned atomic current loops in the iron core?

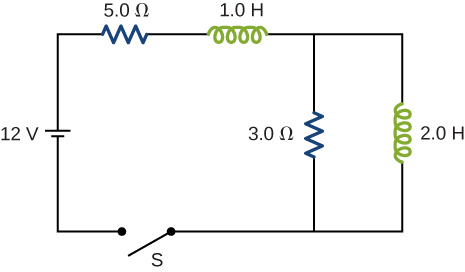
The switch S of the circuit shown below is closed at [latex]t=0[/latex]. Determine (a) the initial current through the battery and (b) the steady-state current through the battery.

A 12 volt battery is connected in series with a 5 ohm resistor, a 1 Henry inductor, a 3 ohm resistor and an open switch S. Parallel to the 3 ohm resistor is a 2 Henry inductor.

Show Solution

a. 0 A; b. 2.4 A

In an oscillating RLC circuit, [latex]R=7.0\phantom{\rule{0.2em}{0ex}}\text{Ω},L=10\phantom{\rule{0.2em}{0ex}}\text{mH},\phantom{\rule{0.2em}{0ex}}\text{and}\phantom{\rule{0.2em}{0ex}}C=3.0\phantom{\rule{0.2em}{0ex}}\mu \text{F}[/latex]. Initially, the capacitor has a charge of [latex]8.0\phantom{\rule{0.2em}{0ex}}\mu \text{C}[/latex] and the current is zero. Calculate the charge on the capacitor (a) five cycles later and (b) 50 cycles later.

A 25.0-H inductor has 100 A of current turned off in 1.00 ms. (a) What voltage is induced to oppose this? (b) What is unreasonable about this result? (c) Which assumption or premise is responsible?

Show Solution

a. [latex]2.50\phantom{\rule{0.2em}{0ex}}×\phantom{\rule{0.2em}{0ex}}{10}^{6}\phantom{\rule{0.2em}{0ex}}\text{V}[/latex]; (b) The voltage is so extremely high that arcing would occur and the current would not be reduced so rapidly. (c) It is not reasonable to shut off such a large current in such a large inductor in such an extremely short time.

Challenge Problems

A coaxial cable has an inner conductor of radius a, and outer thin cylindrical shell of radius b. A current I flows in the inner conductor and returns in the outer conductor. The self-inductance of the structure will depend on how the current in the inner cylinder tends to be distributed. Investigate the following two extreme cases. (a) Let current in the inner conductor be distributed only on the surface and find the self-inductance. (b) Let current in the inner cylinder be distributed uniformly over its cross-section and find the self-inductance. Compare with your results in (a).

In a damped oscillating circuit the energy is dissipated in the resistor. The Q-factor is a measure of the persistence of the oscillator against the dissipative loss. (a) Prove that for a lightly damped circuit the energy, U, in the circuit decreases according to the following equation.

[latex]\frac{dU}{dt}=-2\beta U,[/latex] where [latex]\beta =\frac{R}{2L}.[/latex]

(b) Using the definition of the Q-factor as energy divided by the loss over the next cycle, prove that Q-factor of a lightly damped oscillator as defined in this problem is $latex $

[latex]Q\equiv \frac{{U}_{\text{begin}}}{\text{Δ}{U}_{\text{one cycle}}}=\frac{1}{2\pi R}\sqrt{\frac{L}{C}}.[/latex]

(Hint: For (b), to obtain Q, divide E at the beginning of one cycle by the change [latex]\text{Δ}E[/latex] over the next cycle.)

Show Solution

proof

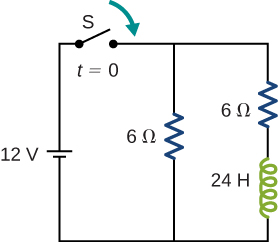
The switch in the circuit shown below is closed at [latex]t=0\phantom{\rule{0.2em}{0ex}}\text{s}[/latex]. Find currents through (a) [latex]{R}_{1}[/latex], (b) [latex]{R}_{2}[/latex], and (c) the battery as function of time.

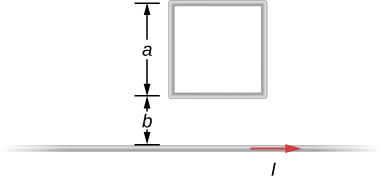
A 12 volt battery is connected to a 6 ohm resistor and a switch S, which is open at time t=0. Connected in parallel with the 6 ohm resistor are another 6 ohm resistor and a 24 Henry inductor.

A square loop of side 2 cm is placed 1 cm from a long wire carrying a current that varies with time at a constant rate of 3 A/s as shown below. (a) Use Ampère’s law and find the magnetic field. (b) Determine the magnetic flux through the loop. (c) If the loop has a resistance of [latex]3\phantom{\rule{0.2em}{0ex}}\text{Ω}[/latex], how much induced current flows in the loop?

A 12 volt battery is connected to a 6 ohm resistor and a switch S, which is open at time t=0. Connected in parallel with the 6 ohm resistor are another 6 ohm resistor and a 24 Henry inductor.

Show Solution

a. [latex]\frac{dB}{dt}=6\phantom{\rule{0.2em}{0ex}}×\phantom{\rule{0.2em}{0ex}}{10}^{-6}\phantom{\rule{0.2em}{0ex}}\text{T/s;}[/latex] b. [latex]\text{Φ}=\frac{{\mu }_{0}aI}{2\pi }\phantom{\rule{0.2em}{0ex}}\text{ln}\phantom{\rule{0.2em}{0ex}}\left(\frac{a+b}{b}\right)[/latex]; c. 4.4 nA

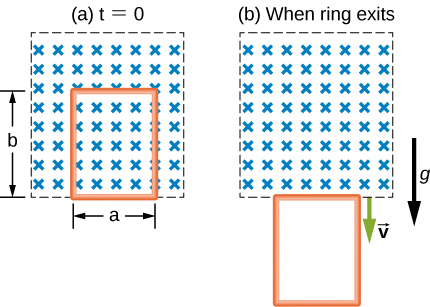
A rectangular copper ring, of mass 100 g and resistance [latex]0.2\phantom{\rule{0.2em}{0ex}}\text{Ω}[/latex], is in a region of uniform magnetic field that is perpendicular to the area enclosed by the ring and horizontal to Earth’s surface. The ring is let go from rest when it is at the edge of the nonzero magnetic field region (see below). (a) Find its speed when the ring just exits the region of uniform magnetic field. (b) If it was let go at [latex]t=0[/latex], what is the time when it exits the region of magnetic field for the following values: [latex]a=25\phantom{\rule{0.2em}{0ex}}\text{cm},\phantom{\rule{0.2em}{0ex}}b=50\phantom{\rule{0.2em}{0ex}}\text{cm},\phantom{\rule{0.2em}{0ex}}B=3\phantom{\rule{0.2em}{0ex}}\text{T},\phantom{\rule{0.2em}{0ex}}\text{and}[/latex] [latex]g=9.8\phantom{\rule{0.2em}{0ex}}{\text{m/s}}^{2}?[/latex] Assume the magnetic field of the induced current is negligible compared to 3 T.

Figure a shows a box with crosses in it. It is labeled t=0. An area within it is demarcated with breadth equal to a and length equal to b. Figure b shows the same box with crosses in it. It is labeled, “when ring exits”. The demarcated are from figure a is now below the box. There are two downward arrows labeled g and v.

Glossary

RLC circuit
circuit with an ac source, resistor, inductor, and capacitor all in series.
Licenses and Attributions

RLC Series Circuits. Authored by: OpenStax College. Located at: https://openstax.org/books/university-physics-volume-2/pages/14-6-rlc-series-circuits. License: CC BY: Attribution. License Terms: Download for free at https://openstax.org/books/university-physics-volume-2/pages/1-introduction

License

Icon for the Creative Commons Attribution 4.0 International License

University Physics Volume 2 Copyright © 2016 by cnxuniphysics is licensed under a Creative Commons Attribution 4.0 International License, except where otherwise noted.

Share This Book