10.5 RC Circuits

Samuel J. Ling; William Moebs; Jeff Sanny

Chapter 10. Direct-Current Circuits

10.5 RC Circuits

Learning Objectives

By the end of the section, you will be able to:

Describe the charging process of a capacitor
Describe the discharging process of a capacitor
List some applications of RC circuits

When you use a flash camera, it takes a few seconds to charge the capacitor that powers the flash. The light flash discharges the capacitor in a tiny fraction of a second. Why does charging take longer than discharging? This question and several other phenomena that involve charging and discharging capacitors are discussed in this module.

Circuits with Resistance and Capacitance

An RC circuit is a circuit containing resistance and capacitance. As presented in Capacitance, the capacitor is an electrical component that stores electric charge, storing energy in an electric field.

Figure 10.38(a) shows a simple RC circuit that employs a dc (direct current) voltage source $ϵ$ , a resistor R, a capacitor C, and a two-position switch. The circuit allows the capacitor to be charged or discharged, depending on the position of the switch. When the switch is moved to position A, the capacitor charges, resulting in the circuit in part (b). When the switch is moved to position B, the capacitor discharges through the resistor.

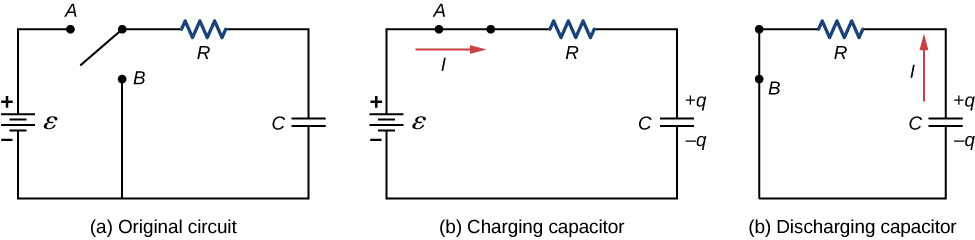
Part a shows an open circuit with three branches, left branch is a voltage source with upward positive terminal connected to point A, the middle branch is a short circuit with point B and right branch is a resistor with a capacitor. Part b shows circuit of part a with first branch connected to third branch. Part c shows circuit of part a with second branch connected to third branch. — **Figure 10.38** (a) An RC circuit with a two-pole switch that can be used to charge and discharge a capacitor. (b) When the switch is moved to position A, the circuit reduces to a simple series connection of the voltage source, the resistor, the capacitor, and the switch. (c) When the switch is moved to position B, the circuit reduces to a simple series connection of the resistor, the capacitor, and the switch. The voltage source is removed from the circuit.

Charging a Capacitor

We can use Kirchhoff’s loop rule to understand the charging of the capacitor. This results in the equation $ϵ - V_{R} - V_{c} = 0.$ This equation can be used to model the charge as a function of time as the capacitor charges. Capacitance is defined as $C = q / V,$ so the voltage across the capacitor is $V_{C} = \frac{q}{C}$ . Using Ohm’s law, the potential drop across the resistor is $V_{R} = I R$ , and the current is defined as $I = d q / d t .$

\begin{matrix} ϵ - V_{R} - V_{c} = 0, \\ ϵ - I R - \frac{q}{C} = 0, \\ ϵ - R \frac{d q}{d t} - \frac{q}{C} = 0. \end{matrix}

This differential equation can be integrated to find an equation for the charge on the capacitor as a function of time.

\begin{matrix} ϵ - R \frac{d q}{d t} - \frac{q}{C} = 0, \\ \frac{d q}{d t} = \frac{ϵ C - q}{R C}, \\ \underset{0}{\int^{q}} \frac{d q}{ϵ C - q} = \frac{1}{R C} \underset{0}{\int^{t}} d t . \end{matrix}

Let $u = ϵ C - q$ , then $d u = − d q .$ The result is

\begin{matrix} - \underset{0}{\int^{q}} \frac{d u}{u} = \frac{1}{R C} \underset{0}{\int^{t}} d t, \\ ln (\frac{ϵ C - q}{ϵ C}) = - \frac{1}{R C} t, \\ \frac{ϵ C - q}{ϵ C} = e^{\frac{− t}{R C}} . \end{matrix}

Simplifying results in an equation for the charge on the charging capacitor as a function of time:

q (t) = C ϵ (1 - e^{- \frac{t}{R C}}) = Q (1 - e^{- \frac{t}{τ}}) .

A graph of the charge on the capacitor versus time is shown in Figure 10.39(a). First note that as time approaches infinity, the exponential goes to zero, so the charge approaches the maximum charge $Q = C ϵ$ and has units of coulombs. The units of RC are seconds, units of time. This quantity is known as the time constant:

τ = R C .

At time $t = τ = R C$ , the charge is equal to $1 - e^{- 1} = 1 - 0.368 = 0.632$ of the maximum charge $Q = C ϵ$ . Notice that the time rate change of the charge is the slope at a point of the charge versus time plot. The slope of the graph is large at time $t = 0.0 s$ and approaches zero as time increases.

As the charge on the capacitor increases, the current through the resistor decreases, as shown in Figure 10.39(b). The current through the resistor can be found by taking the time derivative of the charge.

\begin{matrix} I (t) = \frac{d q}{d t} = \frac{d}{d t} [C ϵ (1 - e^{- \frac{t}{R C}})], \\ I (t) = C ϵ (\frac{1}{R C}) e^{- \frac{t}{R C}} = \frac{ϵ}{R} e^{- \frac{t}{R C}} = I_{o} e^{- \frac{t}{R C}}, \end{matrix}

I (t) = I_{0} e^{− t / τ} .

At time $t = 0.00 s,$ the current through the resistor is $I_{0} = \frac{ϵ}{R}$ . As time approaches infinity, the current approaches zero. At time $t = τ$ , the current through the resistor is $I (t = τ) = I_{0} e^{- 1} = 0.368 I_{0} .$

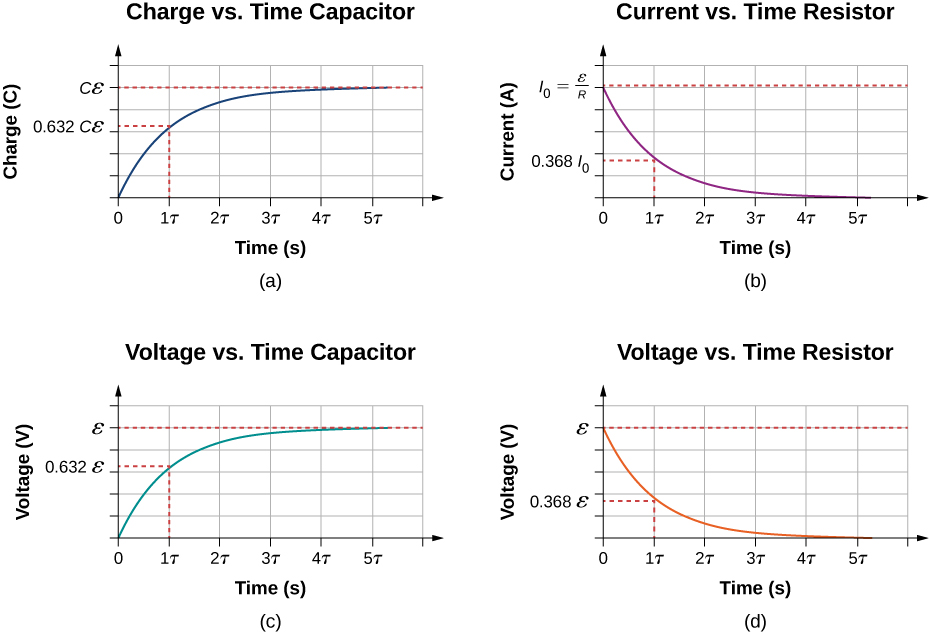
The figure shows four graphs of capacitor charging, with time on the x-axis. Parts a shows charge of the capacitor on the y-axis, the value increases from 0 to Cε and is equal to 0.632 Cε after 1 τ. Parts b shows current of the resistor on the y-axis, the value decreases from I subscript 0 to 0 and is equal to 0.368 I subscript 0 after 1 τ. Parts c shows voltage of the capacitor on the y-axis, the value increases from 0 to ε and is equal to 0.632 ε after 1 τ. Parts d shows voltage of the resistor on the y-axis, the value decreases from ε to 0 and is equal to 0.368 ε after 1 τ. — **Figure 10.39** (a) Charge on the capacitor versus time as the capacitor charges. (b) Current through the resistor versus time. (c) Voltage difference across the capacitor. (d) Voltage difference across the resistor.

Figure 10.39(c) and Figure 10.39(d) show the voltage differences across the capacitor and the resistor, respectively. As the charge on the capacitor increases, the current decreases, as does the voltage difference across the resistor $V_{R} (t) = (I_{0} R) e^{− t / τ} = ϵ e^{− t / τ} .$ The voltage difference across the capacitor increases as $V_{C} (t) = ϵ (1 - e^{− t / τ}) .$

Discharging a Capacitor

When the switch in Figure 10.38(a) is moved to position B, the circuit reduces to the circuit in part (c), and the charged capacitor is allowed to discharge through the resistor. A graph of the charge on the capacitor as a function of time is shown in Figure 10.40(a). Using Kirchhoff’s loop rule to analyze the circuit as the capacitor discharges results in the equation $− V_{R} - V_{c} = 0$ , which simplifies to $I R + \frac{q}{C} = 0$ . Using the definition of current $\frac{d q}{d t} R = - \frac{q}{C}$ and integrating the loop equation yields an equation for the charge on the capacitor as a function of time:

q (t) = Q e^{− t / τ} .

Here, Q is the initial charge on the capacitor and $τ = R C$ is the time constant of the circuit. As shown in the graph, the charge decreases exponentially from the initial charge, approaching zero as time approaches infinity.

The current as a function of time can be found by taking the time derivative of the charge:

I (t) = - \frac{Q}{R C} e^{− t / τ} .

The negative sign shows that the current flows in the opposite direction of the current found when the capacitor is charging. Figure 10.40(b) shows an example of a plot of charge versus time and current versus time. A plot of the voltage difference across the capacitor and the voltage difference across the resistor as a function of time are shown in parts (c) and (d) of the figure. Note that the magnitudes of the charge, current, and voltage all decrease exponentially, approaching zero as time increases.

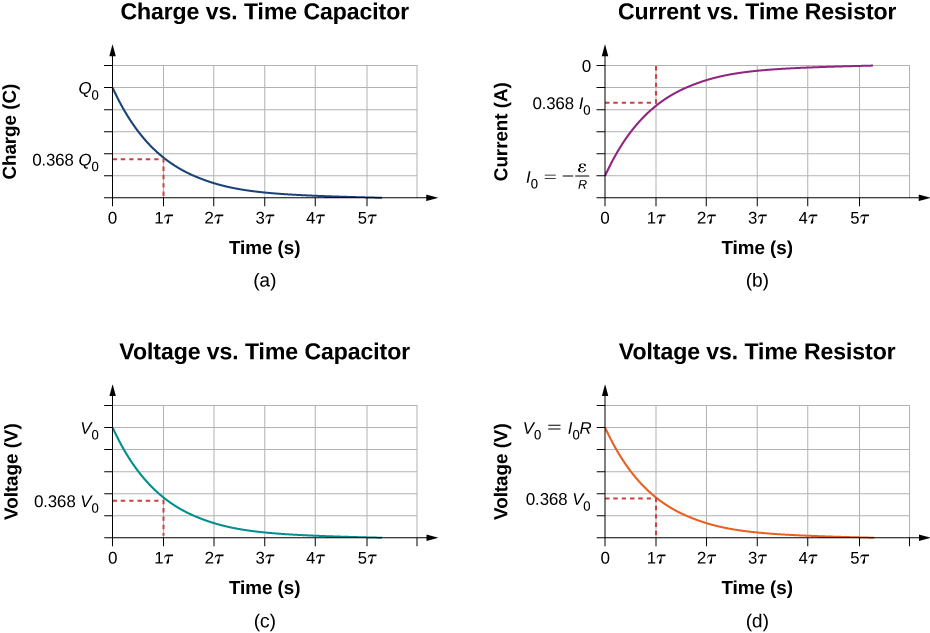
The figure shows four graphs of capacitor discharging, with time on the x-axis. Parts a shows charge of the capacitor on the y-axis, the value decreases from Q subscript 0 to 0 and is equal to 0.368 Q subscript 0 after 1 τ. Parts b shows current of the resistor on the y-axis, the value increases from I subscript 0 to 0 and is equal to 0.368 I subscript 0 after 1 τ. Parts c shows voltage of the capacitor on the y-axis, the value decreases from V subscript 0 to 0 and is equal to 0.368 V subscript 0 after 1 τ. Parts d shows voltage of the resistor on the y-axis, the value decreases from V subscript 0 to 0 and is equal to 0.368 V subscript 0 after 1 τ. — **Figure 10.40** (a) Charge on the capacitor versus time as the capacitor discharges. (b) Current through the resistor versus time. (c) Voltage difference across the capacitor. (d) Voltage difference across the resistor.

Now we can explain why the flash camera mentioned at the beginning of this section takes so much longer to charge than discharge: The resistance while charging is significantly greater than while discharging. The internal resistance of the battery accounts for most of the resistance while charging. As the battery ages, the increasing internal resistance makes the charging process even slower.

Example

The Relaxation Oscillator

One application of an RC circuit is the relaxation oscillator, as shown below. The relaxation oscillator consists of a voltage source, a resistor, a capacitor, and a neon lamp. The neon lamp acts like an open circuit (infinite resistance) until the potential difference across the neon lamp reaches a specific voltage. At that voltage, the lamp acts like a short circuit (zero resistance), and the capacitor discharges through the neon lamp and produces light. In the relaxation oscillator shown, the voltage source charges the capacitor until the voltage across the capacitor is 80 V. When this happens, the neon in the lamp breaks down and allows the capacitor to discharge through the lamp, producing a bright flash. After the capacitor fully discharges through the neon lamp, it begins to charge again, and the process repeats. Assuming that the time it takes the capacitor to discharge is negligible, what is the time interval between flashes?

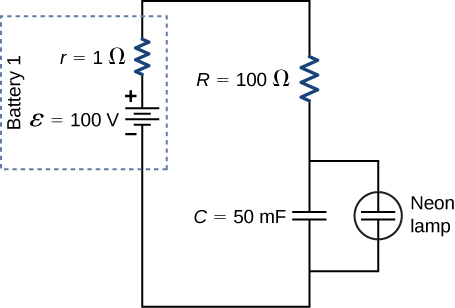
The positive terminal of voltage source of 100 V and internal resistance of 1 Ω is connected to resistor R of 100 Ω and capacitor C of 50 mF. A neon lamp is connected parallel to the capacitor.

Strategy

The time period can be found from considering the equation $V_{C} (t) = ϵ (1 - e^{− t / τ}),$ where $τ = (R + r) C .$

Solution

Show Answer

The neon lamp flashes when the voltage across the capacitor reaches 80 V. The RC time constant is equal to $τ = (R + r) C = (101 Ω) (50 \times 10^{- 3} F) = 5.05 s .$ We can solve the voltage equation for the time it takes the capacitor to reach 80 V:

\begin{array}{ccc} V_{C} (t) & = & ϵ (1 - e^{− t / τ}), \\ e^{− t / τ} & = & 1 - \frac{V_{C} (t)}{ϵ}, \\ ln (e^{− t / τ}) & = & ln (1 - \frac{V_{C} (t)}{ϵ}), \\ t & = & − τ ln (1 - \frac{V_{C} (t)}{ϵ}) = - 5.05 s \cdot ln (1 - \frac{80 V}{100 V}) = 8.13 s . \end{array}

Significance

One application of the relaxation oscillator is for controlling indicator lights that flash at a frequency determined by the values for R and C. In this example, the neon lamp will flash every 8.13 seconds, a frequency of $f = \frac{1}{T} = \frac{1}{8.13 s} = 0.123 Hz .$ The relaxation oscillator has many other practical uses. It is often used in electronic circuits, where the neon lamp is replaced by a transistor or a device known as a tunnel diode. The description of the transistor and tunnel diode is beyond the scope of this chapter, but you can think of them as voltage controlled switches. They are normally open switches, but when the right voltage is applied, the switch closes and conducts. The “switch” can be used to turn on another circuit, turn on a light, or run a small motor. A relaxation oscillator can be used to make the turn signals of your car blink or your cell phone to vibrate.

RC circuits have many applications. They can be used effectively as timers for applications such as intermittent windshield wipers, pace makers, and strobe lights. Some models of intermittent windshield wipers use a variable resistor to adjust the interval between sweeps of the wiper. Increasing the resistance increases the RC time constant, which increases the time between the operation of the wipers.

Another application is the pacemaker. The heart rate is normally controlled by electrical signals, which cause the muscles of the heart to contract and pump blood. When the heart rhythm is abnormal (the heartbeat is too high or too low), pace makers can be used to correct this abnormality. Pacemakers have sensors that detect body motion and breathing to increase the heart rate during physical activities, thus meeting the increased need for blood and oxygen, and an RC timing circuit can be used to control the time between voltage signals to the heart.

Looking ahead to the study of ac circuits (Alternating-Current Circuits), ac voltages vary as sine functions with specific frequencies. Periodic variations in voltage, or electric signals, are often recorded by scientists. These voltage signals could come from music recorded by a microphone or atmospheric data collected by radar. Occasionally, these signals can contain unwanted frequencies known as “noise.” RC filters can be used to filter out the unwanted frequencies.

In the study of electronics, a popular device known as a 555 timer provides timed voltage pulses. The time between pulses is controlled by an RC circuit. These are just a few of the countless applications of RC circuits.

Example

Intermittent Windshield Wipers

A relaxation oscillator is used to control a pair of windshield wipers. The relaxation oscillator consists of a 10.00-mF capacitor and a $10.00 -k Ω$ variable resistor known as a rheostat. A knob connected to the variable resistor allows the resistance to be adjusted from $0.00 Ω$ to $10.00 k Ω .$ The output of the capacitor is used to control a voltage-controlled switch. The switch is normally open, but when the output voltage reaches 10.00 V, the switch closes, energizing an electric motor and discharging the capacitor. The motor causes the windshield wipers to sweep once across the windshield and the capacitor begins to charge again. To what resistance should the rheostat be adjusted for the period of the wiper blades be 10.00 seconds?

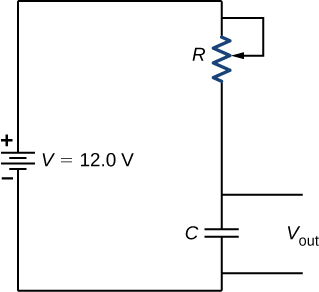
The positive terminal of voltage source V of 12 V is connected to a variable resistor R and capacitor C. V subscript out is measure across C.

Strategy

The resistance considers the equation $V_{out} (t) = V (1 - e^{− t / τ}),$ where $τ = R C .$ The capacitance, output voltage, and voltage of the battery are given. We need to solve this equation for the resistance.

Solution

Show Answer

The output voltage will be 10.00 V and the voltage of the battery is 12.00 V. The capacitance is given as 10.00 mF. Solving for the resistance yields

\begin{matrix} V_{out} (t) & = & V (1 - e^{− t / τ}), \\ e^{− t / R C} & = & 1 - \frac{V_{out} (t)}{V}, \\ ln (e^{− t / R C}) & = & ln (1 - \frac{V_{out} (t)}{V}), \\ - \frac{t}{R C} & = & ln (1 - \frac{V_{out} (t)}{V}), \\ R & = & \frac{− t}{C ln (1 - \frac{V_{C} (t)}{V})} = \frac{- 10.00 s}{10 \times 10^{- 3} F ln (1 - \frac{10 V}{12 V})} = 558.11 Ω . \end{matrix}

Significance

Increasing the resistance increases the time delay between operations of the windshield wipers. When the resistance is zero, the windshield wipers run continuously. At the maximum resistance, the period of the operation of the wipers is:

t = − R C ln (1 - \frac{V_{out} (t)}{V}) = − (10 \times 10^{- 3} F) (10 \times 10^{3} Ω) ln (1 - \frac{10 V}{12 V}) = 179.18 s = 2.98 min .

The RC circuit has thousands of uses and is a very important circuit to study. Not only can it be used to time circuits, it can also be used to filter out unwanted frequencies in a circuit and used in power supplies, like the one for your computer, to help turn ac voltage to dc voltage.

Summary

An RC circuit is one that has both a resistor and a capacitor.
The time constant $τ$ for an RC circuit is $τ = R C .$
When an initially uncharged $(q = 0 at t = 0)$ capacitor in series with a resistor is charged by a dc voltage source, the capacitor asymptotically approaches the maximum charge.
As the charge on the capacitor increases, the current exponentially decreases from the initial current: $I_{0} = ϵ / R .$
If a capacitor with an initial charge Q is discharged through a resistor starting at $t = 0$ , then its charge decreases exponentially. The current flows in the opposite direction, compared to when it charges, and the magnitude of the charge decreases with time.

Conceptual Questions

A battery, switch, capacitor, and lamp are connected in series. Describe what happens to the lamp when the switch is closed.

When making an ECG measurement, it is important to measure voltage variations over small time intervals. The time is limited by the RC constant of the circuit—it is not possible to measure time variations shorter than RC. How would you manipulate R and C in the circuit to allow the necessary measurements?

Show Solution

The time constant can be shortened by using a smaller resistor and/or a smaller capacitor. Care should be taken when reducing the resistance because the initial current will increase as the resistance decreases.

Problems

The timing device in an automobile’s intermittent wiper system is based on an RC time constant and utilizes a $0.500 - μ F$ capacitor and a variable resistor. Over what range must R be made to vary to achieve time constants from 2.00 to 15.0 s?

Show Solution

$4.00 to 30.0 M Ω$

A heart pacemaker fires 72 times a minute, each time a 25.0-nF capacitor is charged (by a battery in series with a resistor) to 0.632 of its full voltage. What is the value of the resistance?

The duration of a photographic flash is related to an RC time constant, which is $0.100 μ F$ for a certain camera. (a) If the resistance of the flash lamp is $0.0400 Ω$ during discharge, what is the size of the capacitor supplying its energy? (b) What is the time constant for charging the capacitor, if the charging resistance is $800 k Ω$ ?

Show Solution

a. $2.50 μ F$ ; b. 2.00 s

A 2.00- and a $7.50 - μ F$ capacitor can be connected in series or parallel, as can a 25.0- and a $100 -k Ω$ resistor. Calculate the four RC time constants possible from connecting the resulting capacitance and resistance in series.

A $500 - Ω$ resistor, an uncharged $1.50 - μ F$ capacitor, and a 6.16-V emf are connected in series. (a) What is the initial current? (b) What is the RC time constant? (c) What is the current after one time constant? (d) What is the voltage on the capacitor after one time constant?

Show Solution

a. 12.3 mA; b. $7.50 \times 10^{- 4} s;$ c. 4.53 mA; d. 3.89 V

A heart defibrillator being used on a patient has an RC time constant of 10.0 ms due to the resistance of the patient and the capacitance of the defibrillator. (a) If the defibrillator has a capacitance of $8.00 μ F,$ what is the resistance of the path through the patient? (You may neglect the capacitance of the patient and the resistance of the defibrillator.) (b) If the initial voltage is 12.0 kV, how long does it take to decline to $6.00 \times 10^{2} V$ ?

An ECG monitor must have an RC time constant less than $1.00 \times 10^{2} μ s$ to be able to measure variations in voltage over small time intervals. (a) If the resistance of the circuit (due mostly to that of the patient’s chest) is $1.00 k Ω$ , what is the maximum capacitance of the circuit? (b) Would it be difficult in practice to limit the capacitance to less than the value found in (a)?

Show Solution

a. $1.00 \times 10^{- 7} F;$ b. No, in practice it would not be difficult to limit the capacitance to less than 100 nF, since typical capacitors range from fractions of a picofarad (pF) to milifarad (mF).

Using the exact exponential treatment, determine how much time is required to charge an initially uncharged 100-pF capacitor through a $75.0 -M Ω$ resistor to $90.0$ of its final voltage.

If you wish to take a picture of a bullet traveling at 500 m/s, then a very brief flash of light produced by an RC discharge through a flash tube can limit blurring. Assuming 1.00 mm of motion during one RC constant is acceptable, and given that the flash is driven by a $600 - μ F$ capacitor, what is the resistance in the flash tube?

Show Solution

$3.33 \times 10^{- 3} Ω$

Glossary

RC circuit: circuit that contains both a resistor and a capacitor

Licenses and Attributions

RC Circuits. Authored by: OpenStax College. Located at: https://openstax.org/books/university-physics-volume-2/pages/10-5-rc-circuits. License: CC BY: Attribution. License Terms: Download for free at https://openstax.org/books/university-physics-volume-2/pages/1-introduction

License

Icon for the Creative Commons Attribution 4.0 International License

Learning Objectives

Circuits with Resistance and Capacitance

Charging a Capacitor

Discharging a Capacitor

Example

The Relaxation Oscillator

Strategy

Solution

Significance

Example

Intermittent Windshield Wipers

Strategy

Solution

Significance

Summary

Conceptual Questions

Problems

Glossary

License

Share This Book