Chapter 14. Inductance

14.5 Oscillations in an LC Circuit

Learning Objectives

By the end of this section, you will be able to:

  • Explain why charge or current oscillates between a capacitor and inductor, respectively, when wired in series
  • Describe the relationship between the charge and current oscillating between a capacitor and inductor wired in series

It is worth noting that both capacitors and inductors store energy, in their electric and magnetic fields, respectively. A circuit containing both an inductor (L) and a capacitor (C) can oscillate without a source of emf by shifting the energy stored in the circuit between the electric and magnetic fields. Thus, the concepts we develop in this section are directly applicable to the exchange of energy between the electric and magnetic fields in electromagnetic waves, or light. We start with an idealized circuit of zero resistance that contains an inductor and a capacitor, an LC circuit.

An LC circuit is shown in Figure 14.16. If the capacitor contains a charge [latex]{q}_{0}[/latex] before the switch is closed, then all the energy of the circuit is initially stored in the electric field of the capacitor (Figure 14.16(a)). This energy is

[latex]{U}_{C}=\frac{1}{2}\phantom{\rule{0.2em}{0ex}}\frac{{q}_{0}^{2}}{C}.[/latex]

When the switch is closed, the capacitor begins to discharge, producing a current in the circuit. The current, in turn, creates a magnetic field in the inductor. The net effect of this process is a transfer of energy from the capacitor, with its diminishing electric field, to the inductor, with its increasing magnetic field.

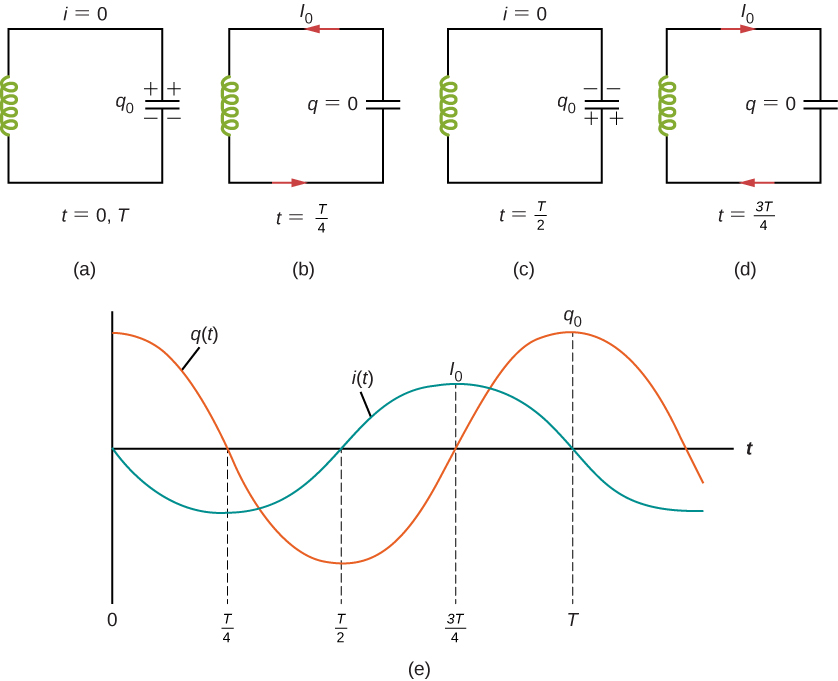
Figures a through d show an inductor connected to a capacitor. Figure a is labeled t = 0, T. The upper plate of the capacitor is positive. No current flows through the circuit. Figure b is labeled t = T by 4. The capacitor discharged. Current I0 flows from the upper plate. Figure c is labeled t = T by 2. The polarity of the capacitor is reversed, with the lower plate being charged positive. No current flows through the circuit. Figure d is labeled 3T by 4. The capacitor is discharged. Current I0 flows from the lower plate. Figure e shows two sine waves. One of them, q0, has highest points of the crest at t = 0 and t = T. It crosses the axis at t = T by 4 and t = 3T by 4. It has the lowest point of the trough at t = T by 2. The second wave, I0 has a smaller amplitude than q0. The highest point of its crest is at t = 3T by 4. The lowest point of its trough is at t = T by 4. It crosses the axis at t = T by 2 and t = T.
Figure 14.16 (a–d) The oscillation of charge storage with changing directions of current in an LC circuit. (e) The graphs show the distribution of charge and current between the capacitor and inductor.

In Figure 14.16(b), the capacitor is completely discharged and all the energy is stored in the magnetic field of the inductor. At this instant, the current is at its maximum value [latex]{I}_{0}[/latex] and the energy in the inductor is

[latex]{U}_{L}=\frac{1}{2}L{I}_{0}^{2}.[/latex]

Since there is no resistance in the circuit, no energy is lost through Joule heating; thus, the maximum energy stored in the capacitor is equal to the maximum energy stored at a later time in the inductor:

[latex]\frac{1}{2}\phantom{\rule{0.2em}{0ex}}\frac{{q}_{0}^{2}}{C}=\frac{1}{2}L{I}_{0}^{2}.[/latex]

At an arbitrary time when the capacitor charge is q(t) and the current is i(t), the total energy U in the circuit is given by

[latex]\frac{{q}^{2}\left(t\right)}{2C}+\frac{L{i}^{2}\left(t\right)}{2}.[/latex]

Because there is no energy dissipation,

[latex]U=\frac{1}{2}\phantom{\rule{0.2em}{0ex}}\frac{{q}^{2}}{C}+\frac{1}{2}L{i}^{2}=\frac{1}{2}\phantom{\rule{0.2em}{0ex}}\frac{{q}_{0}^{2}}{C}=\frac{1}{2}L{I}_{0}^{2}.[/latex]

After reaching its maximum [latex]{I}_{0},[/latex] the current i(t) continues to transport charge between the capacitor plates, thereby recharging the capacitor. Since the inductor resists a change in current, current continues to flow, even though the capacitor is discharged. This continued current causes the capacitor to charge with opposite polarity. The electric field of the capacitor increases while the magnetic field of the inductor diminishes, and the overall effect is a transfer of energy from the inductor back to the capacitor. From the law of energy conservation, the maximum charge that the capacitor re-acquires is [latex]{q}_{0}.[/latex] However, as Figure 14.16(c) shows, the capacitor plates are charged opposite to what they were initially.

When fully charged, the capacitor once again transfers its energy to the inductor until it is again completely discharged, as shown in Figure 14.16(d). Then, in the last part of this cyclic process, energy flows back to the capacitor, and the initial state of the circuit is restored.

We have followed the circuit through one complete cycle. Its electromagnetic oscillations are analogous to the mechanical oscillations of a mass at the end of a spring. In this latter case, energy is transferred back and forth between the mass, which has kinetic energy [latex]m{v}^{2}\text{/}2[/latex], and the spring, which has potential energy [latex]k{x}^{2}\text{/}2[/latex]. With the absence of friction in the mass-spring system, the oscillations would continue indefinitely. Similarly, the oscillations of an LC circuit with no resistance would continue forever if undisturbed; however, this ideal zero-resistance LC circuit is not practical, and any LC circuit will have at least a small resistance, which will radiate and lose energy over time.

The frequency of the oscillations in a resistance-free LC circuit may be found by analogy with the mass-spring system. For the circuit, [latex]i\left(t\right)=dq\left(t\right)\text{/}dt[/latex], the total electromagnetic energy U is

[latex]U=\frac{1}{2}L{i}^{2}+\frac{1}{2}\phantom{\rule{0.2em}{0ex}}\frac{{q}^{2}}{C}.[/latex]

For the mass-spring system, [latex]v\left(t\right)=dx\left(t\right)\text{/}dt[/latex], the total mechanical energy E is

[latex]E=\frac{1}{2}m{v}^{2}+\frac{1}{2}k{x}^{2}.[/latex]

The equivalence of the two systems is clear. To go from the mechanical to the electromagnetic system, we simply replace m by L, v by i, k by 1/C, and x by q. Now x(t) is given by

[latex]x\left(t\right)=A\phantom{\rule{0.2em}{0ex}}\text{cos}\left(\omega t+\varphi \right)[/latex]

where [latex]\omega =\sqrt{k\text{/}m}.[/latex] Hence, the charge on the capacitor in an LC circuit is given by

[latex]q\left(t\right)={q}_{0}\phantom{\rule{0.2em}{0ex}}\text{cos}\left(\omega t+\varphi \right)[/latex]

where the angular frequency of the oscillations in the circuit is

[latex]\omega =\sqrt{\frac{1}{LC}}.[/latex]

Finally, the current in the LC circuit is found by taking the time derivative of q(t):

[latex]i\left(t\right)=\frac{dq\left(t\right)}{dt}=\text{−}\omega {q}_{0}\phantom{\rule{0.2em}{0ex}}\text{sin}\left(\omega t+\varphi \right).[/latex]

The time variations of q and I are shown in Figure 14.16(e) for [latex]\varphi =0[/latex].

Example

An LC Circuit

In an LC circuit, the self-inductance is [latex]2.0\phantom{\rule{0.2em}{0ex}}×\phantom{\rule{0.2em}{0ex}}{10}^{-2}[/latex] H and the capacitance is [latex]8.0\phantom{\rule{0.2em}{0ex}}×\phantom{\rule{0.2em}{0ex}}{10}^{-6}[/latex] F. At [latex]t=0,[/latex] all of the energy is stored in the capacitor, which has charge [latex]1.2\phantom{\rule{0.2em}{0ex}}×\phantom{\rule{0.2em}{0ex}}{10}^{-5}[/latex] C. (a) What is the angular frequency of the oscillations in the circuit? (b) What is the maximum current flowing through circuit? (c) How long does it take the capacitor to become completely discharged? (d) Find an equation that represents q(t).

Strategy

The angular frequency of the LC circuit is given by Equation 14.41. To find the maximum current, the maximum energy in the capacitor is set equal to the maximum energy in the inductor. The time for the capacitor to become discharged if it is initially charged is a quarter of the period of the cycle, so if we calculate the period of the oscillation, we can find out what a quarter of that is to find this time. Lastly, knowing the initial charge and angular frequency, we can set up a cosine equation to find q(t).

Solution

Show Answer
  1. From Equation 14.41, the angular frequency of the oscillations is

    [latex]\omega =\sqrt{\frac{1}{LC}}=\sqrt{\frac{1}{\left(2.0\phantom{\rule{0.2em}{0ex}}×\phantom{\rule{0.2em}{0ex}}{10}^{-2}\phantom{\rule{0.2em}{0ex}}\text{H}\right)\left(8.0\phantom{\rule{0.2em}{0ex}}×\phantom{\rule{0.2em}{0ex}}{10}^{-6}\phantom{\rule{0.2em}{0ex}}\text{F}\right)}}=2.5\phantom{\rule{0.2em}{0ex}}×\phantom{\rule{0.2em}{0ex}}{10}^{3}\phantom{\rule{0.2em}{0ex}}\text{rad/s}.[/latex]
  2. The current is at its maximum [latex]{I}_{0}[/latex] when all the energy is stored in the inductor. From the law of energy conservation,

    [latex]\frac{1}{2}L{I}_{0}^{2}=\frac{1}{2}\phantom{\rule{0.2em}{0ex}}\frac{{q}_{0}^{2}}{C},[/latex]


     so

    [latex]{I}_{0}=\sqrt{\frac{1}{LC}}{q}_{0}=\left(2.5\phantom{\rule{0.2em}{0ex}}×\phantom{\rule{0.2em}{0ex}}{10}^{3}\phantom{\rule{0.2em}{0ex}}\text{rad/s}\right)\left(1.2\phantom{\rule{0.2em}{0ex}}×\phantom{\rule{0.2em}{0ex}}{10}^{-5}\phantom{\rule{0.2em}{0ex}}\text{C}\right)=3.0\phantom{\rule{0.2em}{0ex}}×\phantom{\rule{0.2em}{0ex}}{10}^{-2}\phantom{\rule{0.2em}{0ex}}\text{A}.[/latex]


     This result can also be found by an analogy to simple harmonic motion, where current and charge are the velocity and position of an oscillator.

  3. The capacitor becomes completely discharged in one-fourth of a cycle, or during a time T/4, where T is the period of the oscillations. Since

    [latex]T=\frac{2\pi }{\omega }=\frac{2\pi }{2.5\phantom{\rule{0.2em}{0ex}}×\phantom{\rule{0.2em}{0ex}}{10}^{3}\phantom{\rule{0.2em}{0ex}}\text{rad/s}}=2.5\phantom{\rule{0.2em}{0ex}}×\phantom{\rule{0.2em}{0ex}}{10}^{-3}\phantom{\rule{0.2em}{0ex}}\text{s},[/latex]


     the time taken for the capacitor to become fully discharged is [latex]\left(2.5\phantom{\rule{0.2em}{0ex}}×\phantom{\rule{0.2em}{0ex}}{10}^{-3}\phantom{\rule{0.2em}{0ex}}\text{s}\right)\text{/}4=6.3\phantom{\rule{0.2em}{0ex}}×\phantom{\rule{0.2em}{0ex}}{10}^{-4}\phantom{\rule{0.2em}{0ex}}\text{s}.[/latex]

  4. The capacitor is completely charged at [latex]t=0,[/latex] so [latex]q\left(0\right)={q}_{0}.[/latex] Using Equation 14.20, we obtain

    [latex]q\left(0\right)={q}_{0}={q}_{0}\phantom{\rule{0.2em}{0ex}}\text{cos}\phantom{\rule{0.2em}{0ex}}\varphi .[/latex]


     Thus, [latex]\varphi =0,[/latex] and

    [latex]q\left(t\right)=\left(1.2\phantom{\rule{0.2em}{0ex}}×\phantom{\rule{0.2em}{0ex}}{10}^{-5}\phantom{\rule{0.2em}{0ex}}\text{C}\right)\text{cos}\left(2.5\phantom{\rule{0.2em}{0ex}}×\phantom{\rule{0.2em}{0ex}}{10}^{3}t\right).[/latex]

Significance

The energy relationship set up in part (b) is not the only way we can equate energies. At most times, some energy is stored in the capacitor and some energy is stored in the inductor. We can put both terms on each side of the equation. By examining the circuit only when there is no charge on the capacitor or no current in the inductor, we simplify the energy equation.

Check Your Understanding

The angular frequency of the oscillations in an LC circuit is [latex]2.0\phantom{\rule{0.2em}{0ex}}×\phantom{\rule{0.2em}{0ex}}{10}^{3}[/latex] rad/s. (a) If [latex]L=0.10\phantom{\rule{0.2em}{0ex}}\text{H}[/latex], what is C? (b) Suppose that at [latex]t=0,[/latex] all the energy is stored in the inductor. What is the value of [latex]\varphi ?[/latex] (c) A second identical capacitor is connected in parallel with the original capacitor. What is the angular frequency of this circuit?

Show Solution

a. [latex]2.5\mu \text{F}[/latex]; b. [latex]\pi \text{/}2\phantom{\rule{0.2em}{0ex}}\text{rad or}\phantom{\rule{0.2em}{0ex}}3\pi \text{/}2\phantom{\rule{0.2em}{0ex}}\text{rad}[/latex]; c. [latex]1.4\phantom{\rule{0.2em}{0ex}}×\phantom{\rule{0.2em}{0ex}}{10}^{3}\phantom{\rule{0.2em}{0ex}}\text{rad/s}[/latex]

Summary

  • The energy transferred in an oscillatory manner between the capacitor and inductor in an LC circuit occurs at an angular frequency [latex]\omega =\sqrt{\frac{1}{LC}}[/latex].
  • The charge and current in the circuit are given by

    [latex]\begin{array}{ccc}\hfill q\left(t\right)& =\hfill & {q}_{0}\phantom{\rule{0.2em}{0ex}}\text{cos}\left(\omega t+\varphi \right),\hfill \\ \hfill i\left(t\right)& =\hfill & \text{−}\omega {q}_{0}\phantom{\rule{0.2em}{0ex}}\text{sin}\left(\omega t+\varphi \right).\hfill \end{array}[/latex]

Conceptual Questions

Do Kirchhoff’s rules apply to circuits that contain inductors and capacitors?

Show Solution

yes

Can a circuit element have both capacitance and inductance?

In an LC circuit, what determines the frequency and the amplitude of the energy oscillations in either the inductor or capacitor?

Show Solution

The amplitude of energy oscillations depend on the initial energy of the system. The frequency in a LC circuit depends on the values of inductance and capacitance.

Problems

A 5000-pF capacitor is charged to 100 V and then quickly connected to an 80-mH inductor. Determine (a) the maximum energy stored in the magnetic field of the inductor, (b) the peak value of the current, and (c) the frequency of oscillation of the circuit.

The self-inductance and capacitance of an LC circuit are 0.20 mH and 5.0 pF. What is the angular frequency at which the circuit oscillates?

Show Solution

[latex]\omega =3.2\phantom{\rule{0.2em}{0ex}}×\phantom{\rule{0.2em}{0ex}}{10}^{7}\phantom{\rule{0.2em}{0ex}}\text{rad/s}[/latex]

What is the self-inductance of an LC circuit that oscillates at 60 Hz when the capacitance is [latex]10\phantom{\rule{0.2em}{0ex}}\mu \text{F}[/latex]?

In an oscillating LC circuit, the maximum charge on the capacitor is [latex]2.0\phantom{\rule{0.2em}{0ex}}×\phantom{\rule{0.2em}{0ex}}{10}^{-6}\phantom{\rule{0.2em}{0ex}}\text{C}[/latex] and the maximum current through the inductor is 8.0 mA. (a) What is the period of the oscillations? (b) How much time elapses between an instant when the capacitor is uncharged and the next instant when it is fully charged?

Show Solution

a. [latex]1.57\phantom{\rule{0.2em}{0ex}}×\phantom{\rule{0.2em}{0ex}}{10}^{-6}\phantom{\rule{0.2em}{0ex}}\text{s}[/latex]; b. [latex]3.93\phantom{\rule{0.2em}{0ex}}×\phantom{\rule{0.2em}{0ex}}{10}^{-7}\phantom{\rule{0.2em}{0ex}}\text{s}[/latex]

The self-inductance and capacitance of an oscillating LC circuit are [latex]L=20\phantom{\rule{0.2em}{0ex}}\text{mH and}\phantom{\rule{0.2em}{0ex}}C=1.0\phantom{\rule{0.2em}{0ex}}\mu \text{F},[/latex] respectively. (a) What is the frequency of the oscillations? (b) If the maximum potential difference between the plates of the capacitor is 50 V, what is the maximum current in the circuit?

In an oscillating LC circuit, the maximum charge on the capacitor is [latex]{q}_{m}[/latex]. Determine the charge on the capacitor and the current through the inductor when energy is shared equally between the electric and magnetic fields. Express your answer in terms of [latex]{q}_{m}[/latex], L, and C.

Show Solution

[latex]q=\frac{{q}_{m}}{\sqrt{2}},I=\frac{{q}_{m}}{\sqrt{2LC}}[/latex]

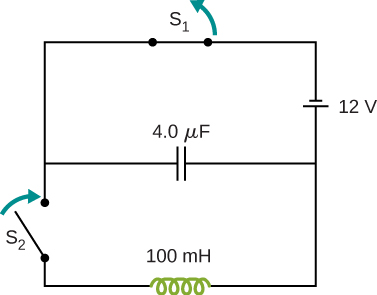
In the circuit shown below, [latex]{\text{S}}_{1}[/latex] is opened and [latex]{\text{S}}_{2}[/latex] is closed simultaneously. Determine (a) the frequency of the resulting oscillations, (b) the maximum charge on the capacitor, (c) the maximum current through the inductor, and (d) the electromagnetic energy of the oscillating circuit.

A 12 volt battery is connected to a 4 microfarad capacitor and a 100 millihenry inductor which are both connected in parallel with each other. There are two switches in the circuit. Switch S1 is closed. If opened, it would open the whole circuit. Switch S2 is open and hence the inductor is currently disconnected.

An LC circuit in an AM tuner (in a car stereo) uses a coil with an inductance of 2.5 mH and a variable capacitor. If the natural frequency of the circuit is to be adjustable over the range 540 to 1600 kHz (the AM broadcast band), what range of capacitance is required?

Show Solution

[latex]\begin{array}{cccccccc}\hfill C& =\hfill & \frac{1}{4{\pi }^{2}{f}^{2}L}\hfill & & & & & \\ \hfill {f}_{1}& =\hfill & 540\phantom{\rule{0.2em}{0ex}}\text{Hz;}\hfill & & & \hfill {C}_{1}& =\hfill & 3.5\phantom{\rule{0.2em}{0ex}}×\phantom{\rule{0.2em}{0ex}}{10}^{-11}\phantom{\rule{0.2em}{0ex}}\text{F}\hfill \\ \hfill {f}_{2}& =\hfill & 1600\phantom{\rule{0.2em}{0ex}}\text{Hz;}\hfill & & & \hfill {C}_{2}& =\hfill & 4.0\phantom{\rule{0.2em}{0ex}}×\phantom{\rule{0.2em}{0ex}}{10}^{-12}\phantom{\rule{0.2em}{0ex}}\text{F}\hfill \end{array}[/latex]

Glossary

LC circuit
circuit composed of an ac source, inductor, and capacitor
Licenses and Attributions

Oscillations in an LC Circuit. Authored by: OpenStax College. Located at: https://openstax.org/books/university-physics-volume-2/pages/14-5-oscillations-in-an-lc-circuit. License: CC BY: Attribution. License Terms: Download for free at https://openstax.org/books/university-physics-volume-2/pages/1-introduction

License

Icon for the Creative Commons Attribution 4.0 International License

University Physics Volume 2 Copyright © 2016 by cnxuniphysics is licensed under a Creative Commons Attribution 4.0 International License, except where otherwise noted.

Share This Book