Mathematical Formulas
Quadratic formula
If [latex]a{x}^{2}+bx+c=0,[/latex] then [latex]x=\frac{\text{−}b±\sqrt{{b}^{2}-4ac}}{2a}[/latex]
| Triangle of base [latex]b[/latex] and height [latex]h[/latex] | Area [latex]=\frac{1}{2}bh[/latex] | |
|---|---|---|
| Circle of radius [latex]r[/latex] | Circumference [latex]=2\pi r[/latex] | Area [latex]=\pi {r}^{2}[/latex] |
| Sphere of radius [latex]r[/latex] | Surface area [latex]=4\pi {r}^{2}[/latex] | Volume [latex]=\frac{4}{3}\pi {r}^{3}[/latex] |
| Cylinder of radius [latex]r[/latex] and height [latex]h[/latex] | Area of curved surface [latex]=2\pi rh[/latex] | Volume [latex]=\pi {r}^{2}h[/latex] |
Trigonometry
Trigonometric Identities
- [latex]\text{sin}\phantom{\rule{0.2em}{0ex}}\theta =1\text{/}\text{csc}\phantom{\rule{0.2em}{0ex}}\theta[/latex]
- [latex]\text{cos}\phantom{\rule{0.2em}{0ex}}\theta =1\text{/}\text{sec}\phantom{\rule{0.2em}{0ex}}\theta[/latex]
- [latex]\text{tan}\phantom{\rule{0.2em}{0ex}}\theta =1\text{/}\text{cot}\phantom{\rule{0.2em}{0ex}}\theta[/latex]
- [latex]\text{sin}\left({90}^{0}-\theta \right)=\text{cos}\phantom{\rule{0.2em}{0ex}}\theta[/latex]
- [latex]\text{cos}\left({90}^{0}-\theta \right)=\text{sin}\phantom{\rule{0.2em}{0ex}}\theta[/latex]
- [latex]\text{tan}\left({90}^{0}-\theta \right)=\text{cot}\phantom{\rule{0.2em}{0ex}}\theta[/latex]
- [latex]{\text{sin}}^{2}\phantom{\rule{0.2em}{0ex}}\theta +{\text{cos}}^{2}\phantom{\rule{0.2em}{0ex}}\theta =1[/latex]
- [latex]{\text{sec}}^{2}\phantom{\rule{0.2em}{0ex}}\theta -{\text{tan}}^{2}\phantom{\rule{0.2em}{0ex}}\theta =1[/latex]
- [latex]\text{tan}\phantom{\rule{0.2em}{0ex}}\theta =\text{sin}\phantom{\rule{0.2em}{0ex}}\theta \text{/}\text{cos}\phantom{\rule{0.2em}{0ex}}\theta[/latex]
- [latex]\text{sin}\left(\alpha ±\beta \right)=\text{sin}\phantom{\rule{0.2em}{0ex}}\alpha \phantom{\rule{0.2em}{0ex}}\text{cos}\phantom{\rule{0.2em}{0ex}}\beta ±\text{cos}\phantom{\rule{0.2em}{0ex}}\alpha \phantom{\rule{0.2em}{0ex}}\text{sin}\phantom{\rule{0.2em}{0ex}}\beta[/latex]
- [latex]\text{cos}\left(\alpha ±\beta \right)=\text{cos}\phantom{\rule{0.2em}{0ex}}\alpha \phantom{\rule{0.2em}{0ex}}\text{cos}\phantom{\rule{0.2em}{0ex}}\beta \mp \text{sin}\phantom{\rule{0.2em}{0ex}}\alpha \phantom{\rule{0.2em}{0ex}}\text{sin}\phantom{\rule{0.2em}{0ex}}\beta[/latex]
- [latex]\text{tan}\left(\alpha ±\beta \right)=\frac{\text{tan}\phantom{\rule{0.2em}{0ex}}\alpha ±\text{tan}\phantom{\rule{0.2em}{0ex}}\beta }{1\mp \text{tan}\phantom{\rule{0.2em}{0ex}}\alpha \phantom{\rule{0.2em}{0ex}}\text{tan}\phantom{\rule{0.2em}{0ex}}\beta }[/latex]
- [latex]\text{sin}\phantom{\rule{0.2em}{0ex}}2\theta =2\text{sin}\phantom{\rule{0.2em}{0ex}}\theta \phantom{\rule{0.2em}{0ex}}\text{cos}\phantom{\rule{0.2em}{0ex}}\theta[/latex]
- [latex]\text{cos}\phantom{\rule{0.2em}{0ex}}2\theta ={\text{cos}}^{2}\phantom{\rule{0.2em}{0ex}}\theta -{\text{sin}}^{2}\phantom{\rule{0.2em}{0ex}}\theta =2\phantom{\rule{0.2em}{0ex}}{\text{cos}}^{2}\phantom{\rule{0.2em}{0ex}}\theta -1=1-2\phantom{\rule{0.2em}{0ex}}{\text{sin}}^{2}\phantom{\rule{0.2em}{0ex}}\theta[/latex]
- [latex]\text{sin}\phantom{\rule{0.2em}{0ex}}\alpha +\text{sin}\phantom{\rule{0.2em}{0ex}}\beta =2\phantom{\rule{0.2em}{0ex}}\text{sin}\frac{1}{2}\left(\alpha +\beta \right)\text{cos}\frac{1}{2}\left(\alpha -\beta \right)[/latex]
- [latex]\text{cos}\phantom{\rule{0.2em}{0ex}}\alpha +\text{cos}\phantom{\rule{0.2em}{0ex}}\beta =2\phantom{\rule{0.2em}{0ex}}\text{cos}\frac{1}{2}\left(\alpha +\beta \right)\text{cos}\frac{1}{2}\left(\alpha -\beta \right)[/latex]
Triangles
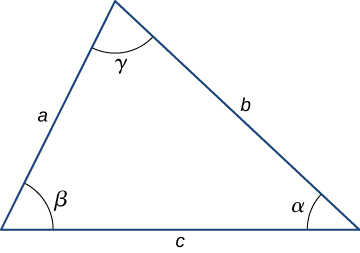
- Law of sines: [latex]\frac{a}{\text{sin}\phantom{\rule{0.2em}{0ex}}\alpha }=\frac{b}{\text{sin}\phantom{\rule{0.2em}{0ex}}\beta }=\frac{c}{\text{sin}\phantom{\rule{0.2em}{0ex}}\gamma }[/latex]
- Law of cosines: [latex]{c}^{2}={a}^{2}+{b}^{2}-2ab\phantom{\rule{0.2em}{0ex}}\text{cos}\phantom{\rule{0.2em}{0ex}}\gamma[/latex]
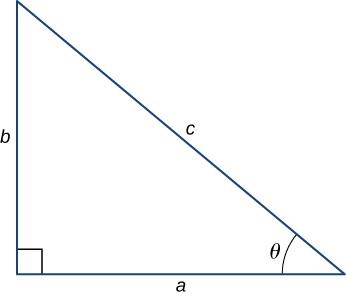
- Pythagorean theorem: [latex]{a}^{2}+{b}^{2}={c}^{2}[/latex]
Series expansions
- Binomial theorem: [latex]{\left(a+b\right)}^{n}={a}^{n}+n{a}^{n-1}b+\frac{n\left(n-1\right){a}^{n-2}{b}^{2}}{2\text{!}}+\frac{n\left(n-1\right)\left(n-2\right){a}^{n-3}{b}^{3}}{3\text{!}}+\text{···}[/latex]
- [latex]{\left(1±x\right)}^{n}=1±\frac{nx}{1\text{!}}+\frac{n\left(n-1\right){x}^{2}}{2\text{!}}±\text{···}\left({x}^{2}< 1\right)[/latex]
- [latex]{\left(1±x\right)}^{\text{−}n}=1\mp \frac{nx}{1\text{!}}+\frac{n\left(n+1\right){x}^{2}}{2\text{!}}\mp \text{···}\left({x}^{2}< 1 \right)[/latex]
- [latex]\text{sin}\phantom{\rule{0.2em}{0ex}}x=x-\frac{{x}^{3}}{3\text{!}}+\frac{{x}^{5}}{5\text{!}}-\text{···}[/latex]
- [latex]\text{cos}\phantom{\rule{0.2em}{0ex}}x=1-\frac{{x}^{2}}{2\text{!}}+\frac{{x}^{4}}{4\text{!}}-\text{···}[/latex]
- [latex]\text{tan}\phantom{\rule{0.2em}{0ex}}x=x+\frac{{x}^{3}}{3}+\frac{2{x}^{5}}{15}+\text{···}[/latex]
- [latex]{e}^{x}=1+x+\frac{{x}^{2}}{2\text{!}}+\text{···}[/latex]
- [latex]\text{ln}\left(1+x\right)=x-\frac{1}{2}{x}^{2}+\frac{1}{3}{x}^{3}-\text{···}\left(|x|< 1\right)[/latex]
Derivatives
- [latex]\frac{d}{dx}\left[af\left(x\right)\right]=a\frac{d}{dx}f\left(x\right)[/latex]
- [latex]\frac{d}{dx}\left[f\left(x\right)+g\left(x\right)\right]=\frac{d}{dx}f\left(x\right)+\frac{d}{dx}g\left(x\right)[/latex]
- [latex]\frac{d}{dx}\left[f\left(x\right)g\left(x\right)\right]=f\left(x\right)\frac{d}{dx}g\left(x\right)+g\left(x\right)\frac{d}{dx}f\left(x\right)[/latex]
- [latex]\frac{d}{dx}f\left(u\right)=\left[\frac{d}{du}f\left(u\right)\right]\frac{du}{dx}[/latex]
- [latex]\frac{d}{dx}{x}^{m}=m{x}^{m-1}[/latex]
- [latex]\frac{d}{dx}\phantom{\rule{0.2em}{0ex}}\text{sin}\phantom{\rule{0.2em}{0ex}}x=\text{cos}\phantom{\rule{0.2em}{0ex}}x[/latex]
- [latex]\frac{d}{dx}\phantom{\rule{0.2em}{0ex}}\text{cos}\phantom{\rule{0.2em}{0ex}}x=\text{−}\text{sin}\phantom{\rule{0.2em}{0ex}}x[/latex]
- [latex]\frac{d}{dx}\phantom{\rule{0.2em}{0ex}}\text{tan}\phantom{\rule{0.2em}{0ex}}x={\text{sec}}^{2}\phantom{\rule{0.2em}{0ex}}x[/latex]
- [latex]\frac{d}{dx}\phantom{\rule{0.2em}{0ex}}\text{cot}\phantom{\rule{0.2em}{0ex}}x=\text{−}{\text{csc}}^{2}\phantom{\rule{0.2em}{0ex}}x[/latex]
- [latex]\frac{d}{dx}\phantom{\rule{0.2em}{0ex}}\text{sec}\phantom{\rule{0.2em}{0ex}}x=\text{tan}\phantom{\rule{0.2em}{0ex}}x\phantom{\rule{0.2em}{0ex}}\text{sec}\phantom{\rule{0.2em}{0ex}}x[/latex]
- [latex]\frac{d}{dx}\phantom{\rule{0.2em}{0ex}}\text{csc}\phantom{\rule{0.2em}{0ex}}x=\text{−}\text{cot}\phantom{\rule{0.2em}{0ex}}x\phantom{\rule{0.2em}{0ex}}\text{csc}\phantom{\rule{0.2em}{0ex}}x[/latex]
- [latex]\frac{d}{dx}{e}^{x}={e}^{x}[/latex]
- [latex]\frac{d}{dx}\phantom{\rule{0.2em}{0ex}}\text{ln}\phantom{\rule{0.2em}{0ex}}x=\frac{1}{x}[/latex]
- [latex]\frac{d}{dx}\phantom{\rule{0.2em}{0ex}}{\text{sin}}^{-1}\phantom{\rule{0.2em}{0ex}}x=\frac{1}{\sqrt{1-{x}^{2}}}[/latex]
- [latex]\frac{d}{dx}\phantom{\rule{0.2em}{0ex}}{\text{cos}}^{-1}x=-\frac{1}{\sqrt{1-{x}^{2}}}[/latex]
- [latex]\frac{d}{dx}\phantom{\rule{0.2em}{0ex}}{\text{tan}}^{-1}x=-\frac{1}{1+{x}^{2}}[/latex]
Integrals
- [latex]\int af\left(x\right)dx=a\int f\left(x\right)dx[/latex]
- [latex]\int \left[f\left(x\right)+g\left(x\right)\right]dx=\int f\left(x\right)dx+\int g\left(x\right)dx[/latex]
- [latex]\begin{array}{cc}\hfill \int {x}^{m}dx& =\frac{{x}^{m+1}}{m+1}\phantom{\rule{0.2em}{0ex}}\left(m\ne \text{−}1\right)\hfill \\ & =\text{ln}\phantom{\rule{0.2em}{0ex}}x\left(m=-1\right)\hfill \end{array}[/latex]
- [latex]\int \text{sin}\phantom{\rule{0.2em}{0ex}}x\phantom{\rule{0.2em}{0ex}}dx=\text{−}\text{cos}\phantom{\rule{0.2em}{0ex}}x[/latex]
- [latex]\int \text{cos}\phantom{\rule{0.2em}{0ex}}x\phantom{\rule{0.2em}{0ex}}dx=\text{sin}\phantom{\rule{0.2em}{0ex}}x[/latex]
- [latex]\int \text{tan}\phantom{\rule{0.2em}{0ex}}x\phantom{\rule{0.2em}{0ex}}dx=\text{ln}|\text{sec}\phantom{\rule{0.2em}{0ex}}x|[/latex]
- [latex]\int {\text{sin}}^{2}\phantom{\rule{0.2em}{0ex}}ax\phantom{\rule{0.2em}{0ex}}dx=\frac{x}{2}-\frac{\text{sin}\phantom{\rule{0.2em}{0ex}}2ax}{4a}[/latex]
- [latex]\int {\text{cos}}^{2}\phantom{\rule{0.2em}{0ex}}ax\phantom{\rule{0.2em}{0ex}}dx=\frac{x}{2}+\frac{\text{sin}\phantom{\rule{0.2em}{0ex}}2ax}{4a}[/latex]
- [latex]\int \text{sin}\phantom{\rule{0.2em}{0ex}}ax\phantom{\rule{0.2em}{0ex}}\text{cos}\phantom{\rule{0.2em}{0ex}}ax\phantom{\rule{0.2em}{0ex}}dx=-\frac{\text{cos}2ax}{4a}[/latex]
- [latex]\int {e}^{ax}\phantom{\rule{0.2em}{0ex}}dx=\frac{1}{a}{e}^{ax}[/latex]
- [latex]\int x{e}^{ax}dx=\frac{{e}^{ax}}{{a}^{2}}\left(ax-1\right)[/latex]
- [latex]\int \text{ln}\phantom{\rule{0.2em}{0ex}}ax\phantom{\rule{0.2em}{0ex}}dx=x\phantom{\rule{0.2em}{0ex}}\text{ln}\phantom{\rule{0.2em}{0ex}}ax-x[/latex]
- [latex]\int \frac{dx}{{a}^{2}+{x}^{2}}=\frac{1}{a}\phantom{\rule{0.2em}{0ex}}{\text{tan}}^{-1}\frac{x}{a}[/latex]
- [latex]\int \frac{dx}{{a}^{2}-{x}^{2}}=\frac{1}{2a}\phantom{\rule{0.2em}{0ex}}\text{ln}|\frac{x+a}{x-a}|[/latex]
- [latex]\int \frac{dx}{\sqrt{{a}^{2}+{x}^{2}}}={\text{sinh}}^{-1}\frac{x}{a}[/latex]
- [latex]\int \frac{dx}{\sqrt{{a}^{2}-{x}^{2}}}={\text{sin}}^{-1}\frac{x}{a}[/latex]
- [latex]\int \sqrt{{a}^{2}+{x}^{2}}\phantom{\rule{0.2em}{0ex}}dx=\frac{x}{2}\sqrt{{a}^{2}+{x}^{2}}+\frac{{a}^{2}}{2}\phantom{\rule{0.2em}{0ex}}{\text{sinh}}^{-1}\frac{x}{a}[/latex]
- [latex]\int \sqrt{{a}^{2}-{x}^{2}}\phantom{\rule{0.2em}{0ex}}dx=\frac{x}{2}\sqrt{{a}^{2}-{x}^{2}}+\frac{{a}^{2}}{2}\phantom{\rule{0.2em}{0ex}}{\text{sin}}^{-1}\frac{x}{a}[/latex]
Licenses and Attributions
Appendix E Mathematical Formulas. Authored by: OpenStax College. Located at: https://openstax.org/books/university-physics-volume-2/pages/e-mathematical-formulas. License: CC BY: Attribution. License Terms: Download for free at https://openstax.org/books/university-physics-volume-2/pages/1-introduction

