15.2 Simple AC Circuits

Samuel J. Ling; William Moebs; Jeff Sanny

Chapter 15. Alternating-Current Circuits

15.2 Simple AC Circuits

Learning Objectives

By the end of the section, you will be able to:

Interpret phasor diagrams and apply them to ac circuits with resistors, capacitors, and inductors
Define the reactance for a resistor, capacitor, and inductor to help understand how current in the circuit behaves compared to each of these devices

In this section, we study simple models of ac voltage sources connected to three circuit components: (1) a resistor, (2) a capacitor, and (3) an inductor. The power furnished by an ac voltage source has an emf given by

v (t) = V_{0} sin ω t,

as shown in Figure 15.4. This sine function assumes we start recording the voltage when it is $v = 0 V$ at a time of $t = 0 s .$ A phase constant may be involved that shifts the function when we start measuring voltages, similar to the phase constant in the waves we studied in Waves. However, because we are free to choose when we start examining the voltage, we can ignore this phase constant for now. We can measure this voltage across the circuit components using one of two methods: (1) a quantitative approach based on our knowledge of circuits, or (2) a graphical approach that is explained in the coming sections.

Figure shows a sine wave with maximum and minimum values of the voltage being V0 and minus V0 respectively. Each positive slope of the wave, at the x-axis, marks one complete wavelength. These points are labeled in sequence: 2 pi by omega, 4 pi by omega and 6 pi by omega. — **Figure 15.4** (a) The output $v (t) = V_{0} sin ω t$ of an ac generator. (b) Symbol used to represent an ac voltage source in a circuit diagram.

Resistor

First, consider a resistor connected across an ac voltage source. From Kirchhoff’s loop rule, the instantaneous voltage across the resistor of Figure 15.5(a) is

v_{R} (t) = V_{0} sin ω t

and the instantaneous current through the resistor is

i_{R} (t) = \frac{v_{R} (t)}{R} = \frac{V_{0}}{R} sin ω t = I_{0} sin ω t .

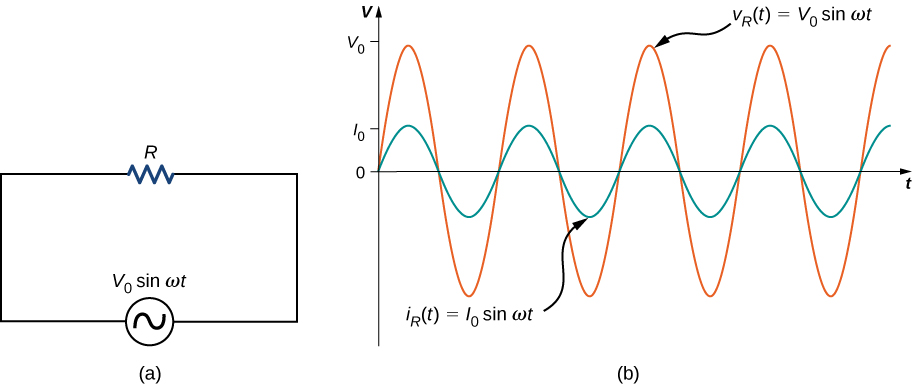
Figure a shows a circuit with an AC voltage source connected to a resistor. The source is labeled V0 sine omega t. Figure b shows sine waves of AC voltage and current on the same graph. Voltage has a greater amplitude than current and its maximum value is marked V0 on the y axis. The maximum value of current is marked I0. The voltage curve is labeled V subscript R parentheses t parentheses equal to V0 sine omega t. The current curve is labeled I subscript R parentheses t parentheses equal to I0 sine omega t. — **Figure 15.5** (a) A resistor connected across an ac voltage source. (b) The current $i_{R} (t)$ through the resistor and the voltage $v_{R} (t)$ across the resistor. The two quantities are in phase.

Here, $I_{0} = V_{0} / R$ is the amplitude of the time-varying current. Plots of $i_{R} (t)$ and $v_{R} (t)$ are shown in Figure 15.5(b). Both curves reach their maxima and minima at the same times, that is, the current through and the voltage across the resistor are in phase.

Graphical representations of the phase relationships between current and voltage are often useful in the analysis of ac circuits. Such representations are called phasor diagrams. The phasor diagram for $i_{R} (t)$ is shown in Figure 15.6(a), with the current on the vertical axis. The arrow (or phasor) is rotating counterclockwise at a constant angular frequency $ω,$ so we are viewing it at one instant in time. If the length of the arrow corresponds to the current amplitude $I_{0},$ the projection of the rotating arrow onto the vertical axis is $i_{R} (t) = I_{0} sin ω t,$ which is the instantaneous current.

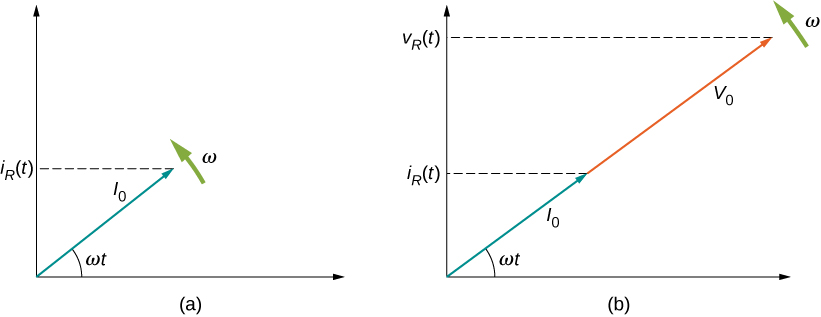
Figure shows the coordinate axes. An arrow labeled V0 starts from the origin and points up and right making an angle omega t with the x axis. An arrow labeled omega is shown near its tip, perpendicular to it, pointing up and left. The tip of the arrow V0 makes a y-intercept labeled V subscript C parentheses t parentheses. An arrow labeled I0 starts at the origin and points up and left. It is perpendicular to V0. It makes a y intercept labeled i subscript C parentheses t parentheses. A arrow labeled omega is shown near its tip, perpendicular to it, pointing down and left. — **Figure 15.6** (a) The phasor diagram representing the current through the resistor of Figure 15.5. (b) The phasor diagram representing both $i_{R} (t)$ and $v_{R} (t)$ .

The vertical axis on a phasor diagram could be either the voltage or the current, depending on the phasor that is being examined. In addition, several quantities can be depicted on the same phasor diagram. For example, both the current $i_{R} (t)$ and the voltage $v_{R} (t)$ are shown in the diagram of Figure 15.6(b). Since they have the same frequency and are in phase, their phasors point in the same direction and rotate together. The relative lengths of the two phasors are arbitrary because they represent different quantities; however, the ratio of the lengths of the two phasors can be represented by the resistance, since one is a voltage phasor and the other is a current phasor.

Capacitor

Now let’s consider a capacitor connected across an ac voltage source. From Kirchhoff’s loop rule, the instantaneous voltage across the capacitor of Figure 15.7(a) is

v_{C} (t) = V_{0} sin ω t .

Recall that the charge in a capacitor is given by $Q = C V .$ This is true at any time measured in the ac cycle of voltage. Consequently, the instantaneous charge on the capacitor is

q (t) = C v_{C} (t) = C V_{0} sin ω t .

Since the current in the circuit is the rate at which charge enters (or leaves) the capacitor,

i_{C} (t) = \frac{d q (t)}{d t} = ω C V_{0} cos ω t = I_{0} cos ω t,

where $I_{0} = ω C V_{0}$ is the current amplitude. Using the trigonometric relationship $cos ω t = sin (ω t + π / 2),$ we may express the instantaneous current as

i_{C} (t) = I_{0} sin (ω t + \frac{π}{2}) .

Dividing $V_{0}$ by $I_{0}$ , we obtain an equation that looks similar to Ohm’s law:

\frac{V_{0}}{I_{0}} = \frac{1}{ω C} = X_{C} .

The quantity $X_{C}$ is analogous to resistance in a dc circuit in the sense that both quantities are a ratio of a voltage to a current. As a result, they have the same unit, the ohm. Keep in mind, however, that a capacitor stores and discharges electric energy, whereas a resistor dissipates it. The quantity $X_{C}$ is known as the capacitive reactance of the capacitor, or the opposition of a capacitor to a change in current. It depends inversely on the frequency of the ac source—high frequency leads to low capacitive reactance.

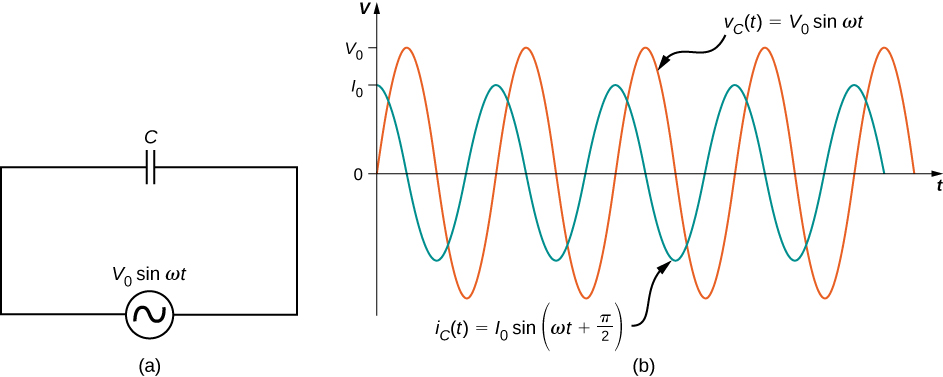
Figure a shows a circuit with an AC voltage source connected to a capacitor. The source is labeled V0 sine omega t. Figure b shows sine waves of AC voltage and current on the same graph. Voltage has a greater amplitude than current and its maximum value is marked V0 on the y axis. The maximum value of current is marked I0. The two curves have the same wavelength but are out of phase by one quarter wavelength. The voltage curve is labeled V subscript C parentheses t parentheses equal to V0 sine omega t. The current curve is labeled I subscript C parentheses t parentheses equal to I0 sine parentheses omega t plus pi by 2 parentheses. — **Figure 15.7** (a) A capacitor connected across an ac generator. (b) The current $i_{C} (t)$ through the capacitor and the voltage $v_{C} (t)$ across the capacitor. Notice that $i_{C} (t)$ leads $v_{C} (t)$ by $π / 2$ rad.

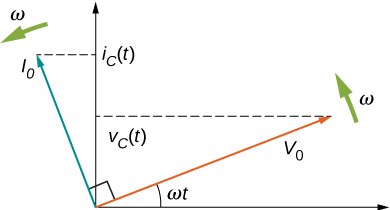
A comparison of the expressions for $v_{C} (t)$ and $i_{C} (t)$ shows that there is a phase difference of $π / 2 rad$ between them. When these two quantities are plotted together, the current peaks a quarter cycle (or $π / 2 rad$ ) ahead of the voltage, as illustrated in Figure 15.7(b). The current through a capacitor leads the voltage across a capacitor by $π / 2 rad,$ or a quarter of a cycle.

The corresponding phasor diagram is shown in Figure 15.8. Here, the relationship between $i_{C} (t)$ and $v_{C} (t)$ is represented by having their phasors rotate at the same angular frequency, with the current phasor leading by $π / 2 rad .$

To this point, we have exclusively been using peak values of the current or voltage in our discussion, namely, $I_{0}$ and $V_{0} .$ However, if we average out the values of current or voltage, these values are zero. Therefore, we often use a second convention called the root mean square value, or rms value, in discussions of current and voltage. The rms operates in reverse of the terminology. First, you square the function, next, you take the mean, and then, you find the square root. As a result, the rms values of current and voltage are not zero. Appliances and devices are commonly quoted with rms values for their operations, rather than peak values. We indicate rms values with a subscript attached to a capital letter (such as $I_{rms}$ ).

Although a capacitor is basically an open circuit, an rms current, or the root mean square of the current, appears in a circuit with an ac voltage applied to a capacitor. Consider that

I_{rms} = \frac{I_{0}}{\sqrt{2}},

where $I_{0}$ is the peak current in an ac system. The rms voltage, or the root mean square of the voltage, is

V_{rms} = \frac{V_{0}}{\sqrt{2}},

where $V_{0}$ is the peak voltage in an ac system. The rms current appears because the voltage is continually reversing, charging, and discharging the capacitor. If the frequency goes to zero, which would be a dc voltage, $X_{C}$ tends to infinity, and the current is zero once the capacitor is charged. At very high frequencies, the capacitor’s reactance tends to zero—it has a negligible reactance and does not impede the current (it acts like a simple wire).

Inductor

Lastly, let’s consider an inductor connected to an ac voltage source. From Kirchhoff’s loop rule, the voltage across the inductor L of Figure 15.9(a) is

v_{L} (t) = V_{0} sin ω t .

The emf across an inductor is equal to $ϵ = − L (d i_{L} / d t);$ however, the potential difference across the inductor is $v_{L} (t) = L d i_{L} (t) / d t$ , because if we consider that the voltage around the loop must equal zero, the voltage gained from the ac source must dissipate through the inductor. Therefore, connecting this with the ac voltage source, we have

\frac{d i_{L} (t)}{d t} = \frac{V_{0}}{L} sin ω t .

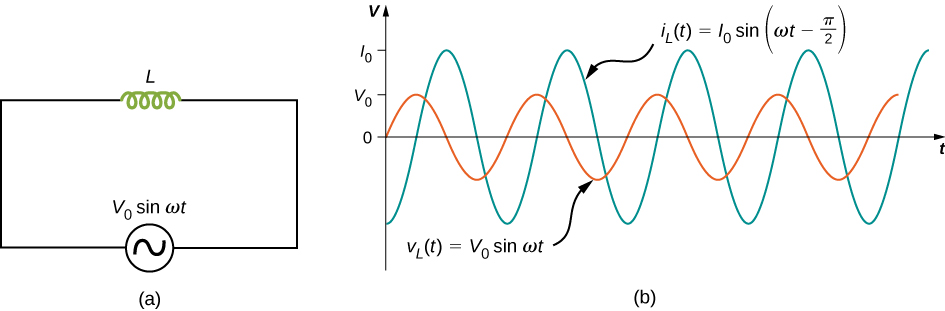
Figure a shows a circuit with an AC voltage source connected to an inductor. The source is labeled V0 sine omega t. Figure b shows sine waves of AC voltage and current on the same graph. Voltage has a smaller amplitude than current and its maximum value is marked V0 on the y axis. The maximum value of current is marked I0. The two curves have the same wavelength but are out of phase by one quarter wavelength. The voltage curve is labeled V subscript L parentheses t parentheses equal to V0 sine omega t. The current curve is labeled I subscript L parentheses t parentheses equal to I0 sine parentheses omega t minus pi by 2 parentheses. — **Figure 15.9** (a) An inductor connected across an ac generator. (b) The current $i_{L} (t)$ through the inductor and the voltage $v_{L} (t)$ across the inductor. Here $i_{L} (t)$ lags $v_{L} (t)$ by $π / 2$ rad.

The current $i_{L} (t)$ is found by integrating this equation. Since the circuit does not contain a source of constant emf, there is no steady current in the circuit. Hence, we can set the constant of integration, which represents the steady current in the circuit, equal to zero, and we have

i_{L} (t) = - \frac{V_{0}}{ω L} cos ω t = \frac{V_{0}}{ω L} sin (ω t - \frac{π}{2}) = I_{0} sin (ω t - \frac{π}{2}),

where $I_{0} = V_{0} / ω L .$ The relationship between $V_{0}$ and $I_{0}$ may also be written in a form analogous to Ohm’s law:

\frac{V_{0}}{I_{0}} = ω L = X_{L} .

The quantity $X_{L}$ is known as the inductive reactance of the inductor, or the opposition of an inductor to a change in current; its unit is also the ohm. Note that $X_{L}$ varies directly as the frequency of the ac source—high frequency causes high inductive reactance.

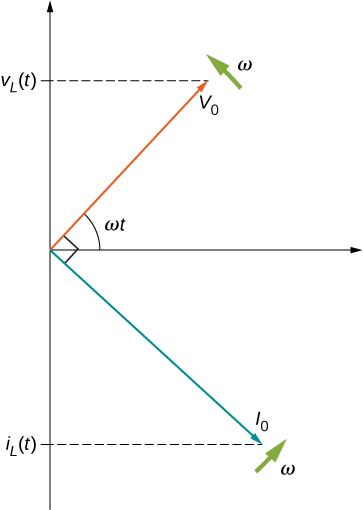
A phase difference of $π / 2$ rad occurs between the current through and the voltage across the inductor. From Equation 15.6 and Equation 15.7, the current through an inductor lags the potential difference across an inductor by $π / 2 rad$ , or a quarter of a cycle. The phasor diagram for this case is shown in Equation 15.10.

An animation from the University of New South Wales AC Circuits illustrates some of the concepts we discuss in this chapter. They also include wave and phasor diagrams that evolve over time so that you can get a better picture of how each changes over time.

Example

Simple AC Circuits

An ac generator produces an emf of amplitude 10 V at a frequency $f = 60 Hz .$ Determine the voltages across and the currents through the circuit elements when the generator is connected to (a) a $100 - Ω$ resistor, (b) a $10 - μ F$ capacitor, and (c) a 15-mH inductor.

Strategy

The entire AC voltage across each device is the same as the source voltage. We can find the currents by finding the reactance X of each device and solving for the peak current using $I_{0} = V_{0} / X .$

Solution

Show Answer

The voltage across the terminals of the source is

v (t) = V_{0} sin ω t = (10 V) sin 120 π t,

where $ω = 2 π f = 120 π rad/s$ is the angular frequency. Since v(t) is also the voltage across each of the elements, we have

v (t) = v_{R} (t) = v_{C} (t) = v_{L} (t) = (10 V) sin 120 π t .

a. When $R = 100 Ω,$ the amplitude of the current through the resistor is

I_{0} = V_{0} / R = 10 V / 100 Ω = 0.10 A,

so

i_{R} (t) = (0.10 A) sin 120 π t .

b. From Equation 15.3, the capacitive reactance is

X_{C} = \frac{1}{ω C} = \frac{1}{(120 π rad/s) (10 \times 10^{- 6} F)} = 265 Ω,

so the maximum value of the current is

I_{0} = \frac{V_{0}}{X_{C}} = \frac{10 V}{265 Ω} = 3.8 \times 10^{- 2} A

and the instantaneous current is given by

i_{C} (t) = (3.8 \times 10^{- 2} A) sin (120 π t + \frac{π}{2}) .

c. From Equation 15.8, the inductive reactance is

X_{L} = ω L = (120 π rad/s) (15 \times 10^{- 3} H) = 5.7 Ω .

The maximum current is therefore

I_{0} = \frac{10 V}{5.7 Ω} = 1.8 A

and the instantaneous current is

i_{L} (t) = (1.8 A) sin (120 π t - \frac{π}{2}) .

Significance

Although the voltage across each device is the same, the peak current has different values, depending on the reactance. The reactance for each device depends on the values of resistance, capacitance, or inductance.

Check Your Understanding

Repeat Example 15.1 for an ac source of amplitude 20 V and frequency 100 Hz.

Show Solution

a. $(20 V) sin 200 π t, (0.20 A) sin 200 π t$ ; b. $(20 V) sin 200 π t, (0.13 A) sin (200 π t + π / 2)$ ; c. $(20 V) sin 200 π t, (2.1 A) sin (200 π t - π / 2)$

Summary

For resistors, the current through and the voltage across are in phase.
For capacitors, we find that when a sinusoidal voltage is applied to a capacitor, the voltage follows the current by one-fourth of a cycle. Since a capacitor can stop current when fully charged, it limits current and offers another form of ac resistance, called capacitive reactance, which has units of ohms.
For inductors in ac circuits, we find that when a sinusoidal voltage is applied to an inductor, the voltage leads the current by one-fourth of a cycle.
The opposition of an inductor to a change in current is expressed as a type of ac reactance. This inductive reactance, which has units of ohms, varies with the frequency of the ac source.

Conceptual Questions

Explain why at high frequencies a capacitor acts as an ac short, whereas an inductor acts as an open circuit.

Problems

Calculate the reactance of a $5.0 - μ F$ capacitor at (a) 60 Hz, (b) 600 Hz, and (c) 6000 Hz.

Show Solution

a. $530 Ω$ ; b. $53 Ω$ ; c. $5.3 Ω$

What is the capacitance of a capacitor whose reactance is $10 Ω$ at 60 Hz?

Calculate the reactance of a 5.0-mH inductor at (a) 60 Hz, (b) 600 Hz, and (c) 6000 Hz.

Show Solution

a. $1.9 Ω$ ; b. $19 Ω$ ; c. $190 Ω$

What is the self-inductance of a coil whose reactance is $10 Ω$ at 60 Hz?

At what frequency is the reactance of a $20 - μ F$ capacitor equal to that of a 10-mH inductor?

Show Solution

360 Hz

At 1000 Hz, the reactance of a 5.0-mH inductor is equal to the reactance of a particular capacitor. What is the capacitance of the capacitor?

A $50 - Ω$ resistor is connected across the emf $v (t) = (160 V) sin (120 π t)$ . Write an expression for the current through the resistor.

Show Solution

$i (t) = (3.2 A) sin (120 π t)$

A $25 - μ F$ capacitor is connected to an emf given by $v (t) = (160 V) sin (120 π t)$ . (a) What is the reactance of the capacitor? (b) Write an expression for the current output of the source.

A 100-mH inductor is connected across the emf of the preceding problem. (a) What is the reactance of the inductor? (b) Write an expression for the current through the inductor.

Show Solution

a. $38 Ω$ ; b. $i (t) = (4.24 A) sin (120 π t - π / 2)$

Glossary

capacitive reactance: opposition of a capacitor to a change in current

inductive reactance: opposition of an inductor to a change in current

rms current: root mean square of the current

rms voltage: root mean square of the voltage

Licenses and Attributions

Simple AC Circuits. Authored by: OpenStax College. Located at: https://openstax.org/books/university-physics-volume-2/pages/15-2-simple-ac-circuits. License: CC BY: Attribution. License Terms: Download for free at https://openstax.org/books/university-physics-volume-2/pages/1-introduction

License

Icon for the Creative Commons Attribution 4.0 International License

Learning Objectives

Resistor

Capacitor

Inductor

Example

Simple AC Circuits

Strategy

Solution

Significance

Check Your Understanding

Summary

Conceptual Questions

Problems

Glossary

License

Share This Book