Chapter 7. Electric Potential
7.1 Electric Potential Energy
Learning Objectives
By the end of this section, you will be able to:
- Define the work done by an electric force
- Define electric potential energy
- Apply work and potential energy in systems with electric charges
When a free positive charge q is accelerated by an electric field, it is given kinetic energy (Figure 7.2). The process is analogous to an object being accelerated by a gravitational field, as if the charge were going down an electrical hill where its electric potential energy is converted into kinetic energy, although of course the sources of the forces are very different. Let us explore the work done on a charge q by the electric field in this process, so that we may develop a definition of electric potential energy.
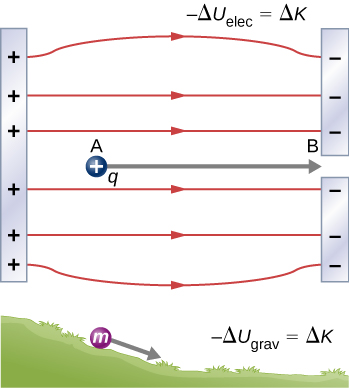
The electrostatic or Coulomb force is conservative, which means that the work done on q is independent of the path taken, as we will demonstrate later. This is exactly analogous to the gravitational force. When a force is conservative, it is possible to define a potential energy associated with the force. It is usually easier to work with the potential energy (because it depends only on position) than to calculate the work directly.
To show this explicitly, consider an electric charge [latex]+q[/latex] fixed at the origin and move another charge [latex]+Q[/latex] toward q in such a manner that, at each instant, the applied force [latex]\stackrel{\to }{\textbf{F}}[/latex] exactly balances the electric force [latex]{\stackrel{\to }{\textbf{F}}}_{e}[/latex] on Q (Figure 7.3). The work done by the applied force [latex]\stackrel{\to }{\textbf{F}}[/latex] on the charge Q changes the potential energy of Q. We call this potential energy the electrical potential energy of Q.
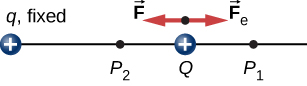
The work [latex]{W}_{12}[/latex] done by the applied force [latex]\stackrel{\to }{\textbf{F}}[/latex] when the particle moves from [latex]{P}_{1}[/latex] to [latex]{P}_{2}[/latex] may be calculated by
Since the applied force [latex]\stackrel{\to }{\textbf{F}}[/latex] balances the electric force [latex]{\stackrel{\to }{\textbf{F}}}_{e}[/latex] on Q, the two forces have equal magnitude and opposite directions. Therefore, the applied force is
where we have defined positive to be pointing away from the origin and r is the distance from the origin. The directions of both the displacement and the applied force in the system in Figure 7.3 are parallel, and thus the work done on the system is positive.
We use the letter U to denote electric potential energy, which has units of joules (J). When a conservative force does negative work, the system gains potential energy. When a conservative force does positive work, the system loses potential energy, [latex]\text{Δ}U=\text{−}W.[/latex] In the system in Figure 7.3, the Coulomb force acts in the opposite direction to the displacement; therefore, the work is negative. However, we have increased the potential energy in the two-charge system.
Example
Kinetic Energy of a Charged Particle
A [latex]+3.0\text{-nC}[/latex] charge Q is initially at rest a distance of 10 cm ([latex]{r}_{1}[/latex]) from a [latex]+5.0\text{-nC}[/latex] charge q fixed at the origin (Figure 7.4). Naturally, the Coulomb force accelerates Q away from q, eventually reaching 15 cm ([latex]{r}_{2}[/latex]).
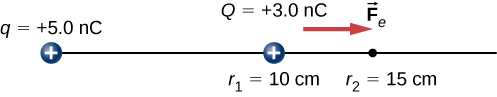
- What is the work done by the electric field between [latex]{r}_{1}[/latex] and [latex]{r}_{2}[/latex]?
- How much kinetic energy does Q have at [latex]{r}_{2}[/latex]?
Strategy
Calculate the work with the usual definition. Since Q started from rest, this is the same as the kinetic energy.
Solution
Show Answer
Integrating force over distance, we obtain
This is also the value of the kinetic energy at [latex]{r}_{2}.[/latex]
Significance
Charge Q was initially at rest; the electric field of q did work on Q, so now Q has kinetic energy equal to the work done by the electric field.
Check Your Understanding
If Q has a mass of [latex]4.00\phantom{\rule{0.2em}{0ex}}\mu \text{g},[/latex] what is the speed of Q at [latex]{r}_{2}?[/latex]
Show Solution
[latex]K=\frac{1}{2}\phantom{\rule{0.2em}{0ex}}m{v}^{2},\phantom{\rule{0.2em}{0ex}}v=\sqrt{2\frac{K}{m}}=\sqrt{2\frac{4.5\phantom{\rule{0.2em}{0ex}}×\phantom{\rule{0.2em}{0ex}}{10}^{-7}\phantom{\rule{0.2em}{0ex}}\text{J}}{4.00\phantom{\rule{0.2em}{0ex}}×\phantom{\rule{0.2em}{0ex}}{10}^{-9}\phantom{\rule{0.2em}{0ex}}\text{kg}}}=15\phantom{\rule{0.2em}{0ex}}\text{m/s}[/latex]
In this example, the work W done to accelerate a positive charge from rest is positive and results from a loss in U, or a negative [latex]\text{Δ}U[/latex]. A value for U can be found at any point by taking one point as a reference and calculating the work needed to move a charge to the other point.
Electric Potential Energy
Work W done to accelerate a positive charge from rest is positive and results from a loss in U, or a negative [latex]\text{Δ}U[/latex]. Mathematically,
Gravitational potential energy and electric potential energy are quite analogous. Potential energy accounts for work done by a conservative force and gives added insight regarding energy and energy transformation without the necessity of dealing with the force directly. It is much more common, for example, to use the concept of electric potential energy than to deal with the Coulomb force directly in real-world applications.
In polar coordinates with q at the origin and Q located at r, the displacement element vector is [latex]d\stackrel{\to }{\textbf{l}}=\hat{\textbf{r}}\phantom{\rule{0.2em}{0ex}}dr[/latex] and thus the work becomes
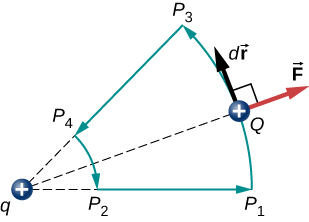
Notice that this result only depends on the endpoints and is otherwise independent of the path taken. To explore this further, compare path [latex]{P}_{1}[/latex] to [latex]{P}_{2}[/latex] with path [latex]{P}_{1}{P}_{3}{P}_{4}{P}_{2}[/latex] in Figure 7.5.
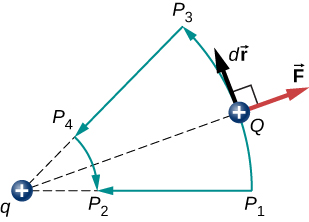
The segments [latex]{P}_{1}{P}_{3}[/latex] and [latex]{P}_{4}{P}_{2}[/latex] are arcs of circles centered at q. Since the force on Q points either toward or away from q, no work is done by a force balancing the electric force, because it is perpendicular to the displacement along these arcs. Therefore, the only work done is along segment [latex]{P}_{3}{P}_{4},[/latex] which is identical to [latex]{P}_{1}{P}_{2}.[/latex]
One implication of this work calculation is that if we were to go around the path [latex]{P}_{1}{P}_{3}{P}_{4}{P}_{2}{P}_{1},[/latex] the net work would be zero (Figure 7.6). Recall that this is how we determine whether a force is conservative or not. Hence, because the electric force is related to the electric field by [latex]\stackrel{\to }{\textbf{F}}=q\stackrel{\to }{\textbf{E}}[/latex], the electric field is itself conservative. That is,
Note that Q is a constant.
Another implication is that we may define an electric potential energy. Recall that the work done by a conservative force is also expressed as the difference in the potential energy corresponding to that force. Therefore, the work [latex]{W}_{\text{ref}}[/latex] to bring a charge from a reference point to a point of interest may be written as
and, by Equation 7.1, the difference in potential energy [latex]\left({U}_{2}-{U}_{1}\right)[/latex] of the test charge Q between the two points is
Therefore, we can write a general expression for the potential energy of two point charges (in spherical coordinates):
We may take the second term to be an arbitrary constant reference level, which serves as the zero reference:
A convenient choice of reference that relies on our common sense is that when the two charges are infinitely far apart, there is no interaction between them. (Recall the discussion of reference potential energy in Potential Energy and Conservation of Energy.) Taking the potential energy of this state to be zero removes the term [latex]{U}_{\text{ref}}[/latex] from the equation (just like when we say the ground is zero potential energy in a gravitational potential energy problem), and the potential energy of Q when it is separated from q by a distance r assumes the form
This formula is symmetrical with respect to q and Q, so it is best described as the potential energy of the two-charge system.
Example
Potential Energy of a Charged Particle
A [latex]+3.0\text{-nC}[/latex] charge Q is initially at rest a distance of 10 cm ([latex]{r}_{1}[/latex]) from a [latex]\text{+5}\text{.0-nC}[/latex] charge q fixed at the origin (Figure 7.7). Naturally, the Coulomb force accelerates Q away from q, eventually reaching 15 cm ([latex]{r}_{2}[/latex]).
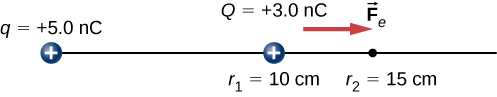
What is the change in the potential energy of the two-charge system from [latex]{r}_{1}[/latex] to [latex]{r}_{2}?[/latex]
Strategy
Calculate the potential energy with the definition given above: [latex]\text{Δ}{U}_{12}=\text{−}{\int }_{{r}_{1}}^{{r}_{2}}\stackrel{\to }{\textbf{F}}·d\stackrel{\to }{\textbf{r}}.[/latex] Since Q started from rest, this is the same as the kinetic energy.
Solution
Show Answer
We have
Significance
The change in the potential energy is negative, as expected, and equal in magnitude to the change in kinetic energy in this system. Recall from Example 7.1 that the change in kinetic energy was positive.
Check Your Understanding
What is the potential energy of Q relative to the zero reference at infinity at [latex]{r}_{2}[/latex] in the above example?
Show Solution
It has kinetic energy of [latex]4.5\phantom{\rule{0.2em}{0ex}}×\phantom{\rule{0.2em}{0ex}}{10}^{-7}\phantom{\rule{0.2em}{0ex}}\text{J}[/latex] at point [latex]{r}_{2}[/latex] and potential energy of [latex]9.0\phantom{\rule{0.2em}{0ex}}×\phantom{\rule{0.2em}{0ex}}{10}^{-7}\phantom{\rule{0.2em}{0ex}}\text{J},[/latex] which means that as Q approaches infinity, its kinetic energy totals three times the kinetic energy at [latex]{r}_{2},[/latex] since all of the potential energy gets converted to kinetic.
Due to Coulomb’s law, the forces due to multiple charges on a test charge Q superimpose; they may be calculated individually and then added. This implies that the work integrals and hence the resulting potential energies exhibit the same behavior. To demonstrate this, we consider an example of assembling a system of four charges.
Example
Assembling Four Positive Charges
Find the amount of work an external agent must do in assembling four charges [latex]+2.0\phantom{\rule{0.2em}{0ex}}\mu \text{C},[/latex][latex]+3.0\phantom{\rule{0.2em}{0ex}}\mu \text{C},\phantom{\rule{0.2em}{0ex}}+4.0\phantom{\rule{0.2em}{0ex}}\mu \text{C},[/latex] and [latex]+5.0\phantom{\rule{0.2em}{0ex}}\mu \text{C}[/latex] at the vertices of a square of side 1.0 cm, starting each charge from infinity (Figure 7.8).
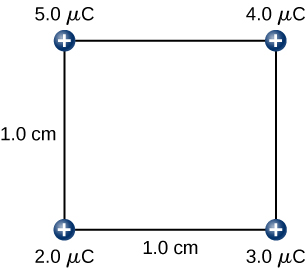
Strategy
We bring in the charges one at a time, giving them starting locations at infinity and calculating the work to bring them in from infinity to their final location. We do this in order of increasing charge.
Solution
Show Answer
Step 1. First bring the [latex]+2.0\text{-}\mu \text{C}[/latex] charge to the origin. Since there are no other charges at a finite distance from this charge yet, no work is done in bringing it from infinity,
Step 2. While keeping the [latex]+2.0\text{-}\mu \text{C}[/latex] charge fixed at the origin, bring the [latex]+3.0\text{-}\mu \text{C}[/latex] charge to [latex]\left(x,y,z\right)=\left(1.0\phantom{\rule{0.2em}{0ex}}\text{cm},0,0\right)[/latex] (Figure 7.9). Now, the applied force must do work against the force exerted by the [latex]+2.0\text{-}\mu \text{C}[/latex] charge fixed at the origin. The work done equals the change in the potential energy of the [latex]+3.0\text{-}\mu \text{C}[/latex] charge:
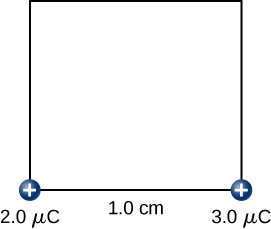
Step 3. While keeping the charges of [latex]+2.0\phantom{\rule{0.2em}{0ex}}\mu \text{C}[/latex] and [latex]+3.0\phantom{\rule{0.2em}{0ex}}\mu \text{C}[/latex] fixed in their places, bring in the [latex]+4.0\text{-}\mu \text{C}[/latex] charge to [latex]\left(x,y,z\right)=\left(1.0\phantom{\rule{0.2em}{0ex}}\text{cm},1.0\phantom{\rule{0.2em}{0ex}}\text{cm},0\right)[/latex] (Figure 7.10). The work done in this step is
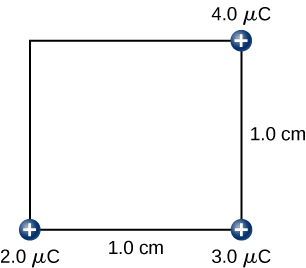
Step 4. Finally, while keeping the first three charges in their places, bring the [latex]+5.0\text{-}\mu \text{C}[/latex] charge to [latex]\left(x,y,z\right)=\left(0,\phantom{\rule{0.2em}{0ex}}1.0\phantom{\rule{0.2em}{0ex}}\text{cm},\phantom{\rule{0.2em}{0ex}}0\right)[/latex] (Figure 7.11). The work done here is

Hence, the total work done by the applied force in assembling the four charges is equal to the sum of the work in bringing each charge from infinity to its final position:
Significance
The work on each charge depends only on its pairwise interactions with the other charges. No more complicated interactions need to be considered; the work on the third charge only depends on its interaction with the first and second charges, the interaction between the first and second charge does not affect the third.
Check Your Understanding
Is the electrical potential energy of two point charges positive or negative if the charges are of the same sign? Opposite signs? How does this relate to the work necessary to bring the charges into proximity from infinity?
Show Solution
positive, negative, and these quantities are the same as the work you would need to do to bring the charges in from infinity
Note that the electrical potential energy is positive if the two charges are of the same type, either positive or negative, and negative if the two charges are of opposite types. This makes sense if you think of the change in the potential energy [latex]\text{Δ}U[/latex] as you bring the two charges closer or move them farther apart. Depending on the relative types of charges, you may have to work on the system or the system would do work on you, that is, your work is either positive or negative. If you have to do positive work on the system (actually push the charges closer), then the energy of the system should increase. If you bring two positive charges or two negative charges closer, you have to do positive work on the system, which raises their potential energy. Since potential energy is proportional to 1/r, the potential energy goes up when r goes down between two positive or two negative charges.
On the other hand, if you bring a positive and a negative charge nearer, you have to do negative work on the system (the charges are pulling you), which means that you take energy away from the system. This reduces the potential energy. Since potential energy is negative in the case of a positive and a negative charge pair, the increase in 1/r makes the potential energy more negative, which is the same as a reduction in potential energy.
The result from Example 7.1 may be extended to systems with any arbitrary number of charges. In this case, it is most convenient to write the formula as
The factor of 1/2 accounts for adding each pair of charges twice.
Summary
- The work done to move a charge from point A to B in an electric field is path independent, and the work around a closed path is zero. Therefore, the electric field and electric force are conservative.
- We can define an electric potential energy, which between point charges is [latex]U\left(r\right)=k\frac{qQ}{r}[/latex], with the zero reference taken to be at infinity.
- The superposition principle holds for electric potential energy; the potential energy of a system of multiple charges is the sum of the potential energies of the individual pairs.
Conceptual Questions
Would electric potential energy be meaningful if the electric field were not conservative?
Show Solution
No. We can only define potential energies for conservative fields.
Why do we need to be careful about work done on the system versus work done by the system in calculations?
Does the order in which we assemble a system of point charges affect the total work done?
Show Solution
No, though certain orderings may be simpler to compute.
Problems
Consider a charge [latex]{Q}_{1}\left(+5.0\phantom{\rule{0.2em}{0ex}}\mu \text{C}\right)[/latex] fixed at a site with another charge [latex]{Q}_{2}[/latex] (charge [latex]+3.0\phantom{\rule{0.2em}{0ex}}\mu \text{C}[/latex], mass [latex]6.0\phantom{\rule{0.2em}{0ex}}\mu \text{g}[/latex]) moving in the neighboring space. (a) Evaluate the potential energy of [latex]{Q}_{2}[/latex] when it is 4.0 cm from [latex]{Q}_{1}.[/latex] (b) If [latex]{Q}_{2}[/latex] starts from rest from a point 4.0 cm from [latex]{Q}_{1},[/latex] what will be its speed when it is 8.0 cm from [latex]{Q}_{1}[/latex]? (Note: [latex]{Q}_{1}[/latex] is held fixed in its place.)
Show Solution
a. [latex]U=3.4\phantom{\rule{0.2em}{0ex}}\text{J;}[/latex]
b. [latex]\frac{1}{2}m{v}^{2}={Q}_{1}{Q}_{2}\left(\frac{1}{{r}_{i}}-\frac{1}{{r}_{f}}\right)\to v=2.4x{10}^{4}\phantom{\rule{0.2em}{0ex}}\text{m/s}[/latex]
Two charges [latex]{Q}_{1}\left(+2.00\phantom{\rule{0.2em}{0ex}}\mu \text{C}\right)[/latex] and [latex]{Q}_{2}\left(+2.00\phantom{\rule{0.2em}{0ex}}\mu \text{C}\right)[/latex] are placed symmetrically along the x-axis at [latex]x=±3.00\phantom{\rule{0.2em}{0ex}}\text{cm}[/latex]. Consider a charge [latex]{Q}_{3}[/latex] of charge [latex]+4.00\phantom{\rule{0.2em}{0ex}}\mu \text{C}[/latex] and mass 10.0 mg moving along the y-axis. If [latex]{Q}_{3}[/latex] starts from rest at [latex]y=2.00\phantom{\rule{0.2em}{0ex}}\text{cm,}[/latex] what is its speed when it reaches [latex]y=4.00\phantom{\rule{0.2em}{0ex}}\text{cm?}[/latex]
To form a hydrogen atom, a proton is fixed at a point and an electron is brought from far away to a distance of [latex]0.529\phantom{\rule{0.2em}{0ex}}×\phantom{\rule{0.2em}{0ex}}{10}^{-10}\phantom{\rule{0.2em}{0ex}}\text{m,}[/latex] the average distance between proton and electron in a hydrogen atom. How much work is done?
Show Solution
[latex]U=4.36\phantom{\rule{0.2em}{0ex}}×\phantom{\rule{0.2em}{0ex}}{10}^{-18}\phantom{\rule{0.2em}{0ex}}\text{J}\phantom{\rule{0.2em}{0ex}}[/latex]
(a) What is the average power output of a heart defibrillator that dissipates 400 J of energy in 10.0 ms? (b) Considering the high-power output, why doesn’t the defibrillator produce serious burns?
Glossary
- electric potential energy
- potential energy stored in a system of charged objects due to the charges
Licenses and Attributions
Electric Potential Energy. Authored by: OpenStax College. Located at: https://openstax.org/books/university-physics-volume-2/pages/7-1-electric-potential-energy. License: CC BY: Attribution. License Terms: Download for free at https://openstax.org/books/university-physics-volume-2/pages/1-introduction

