16 Waves
16.6 Standing Waves and Resonance
Learning Objectives
By the end of this section, you will be able to:
- Describe standing waves and explain how they are produced
- Describe the modes of a standing wave on a string
- Provide examples of standing waves beyond the waves on a string
Throughout this chapter, we have been studying traveling waves, or waves that transport energy from one place to another. Under certain conditions, waves can bounce back and forth through a particular region, effectively becoming stationary. These are called standing waves.
Another related effect is known as resonance. In Oscillations, we defined resonance as a phenomenon in which a small-amplitude driving force could produce large-amplitude motion. Think of a child on a swing, which can be modeled as a physical pendulum. Relatively small-amplitude pushes by a parent can produce large-amplitude swings. Sometimes this resonance is good—for example, when producing music with a stringed instrument. At other times, the effects can be devastating, such as the collapse of a building during an earthquake. In the case of standing waves, the relatively large amplitude standing waves are produced by the superposition of smaller amplitude component waves.
Standing Waves
Sometimes waves do not seem to move; rather, they just vibrate in place. You can see unmoving waves on the surface of a glass of milk in a refrigerator, for example. Vibrations from the refrigerator motor create waves on the milk that oscillate up and down but do not seem to move across the surface. Figure shows an experiment you can try at home. Take a bowl of milk and place it on a common box fan. Vibrations from the fan will produce circular standing waves in the milk. The waves are visible in the photo due to the reflection from a lamp. These waves are formed by the superposition of two or more traveling waves, such as illustrated in Figure for two identical waves moving in opposite directions. The waves move through each other with their disturbances adding as they go by. If the two waves have the same amplitude and wavelength, then they alternate between constructive and destructive interference. The resultant looks like a wave standing in place and, thus, is called a standing wave.

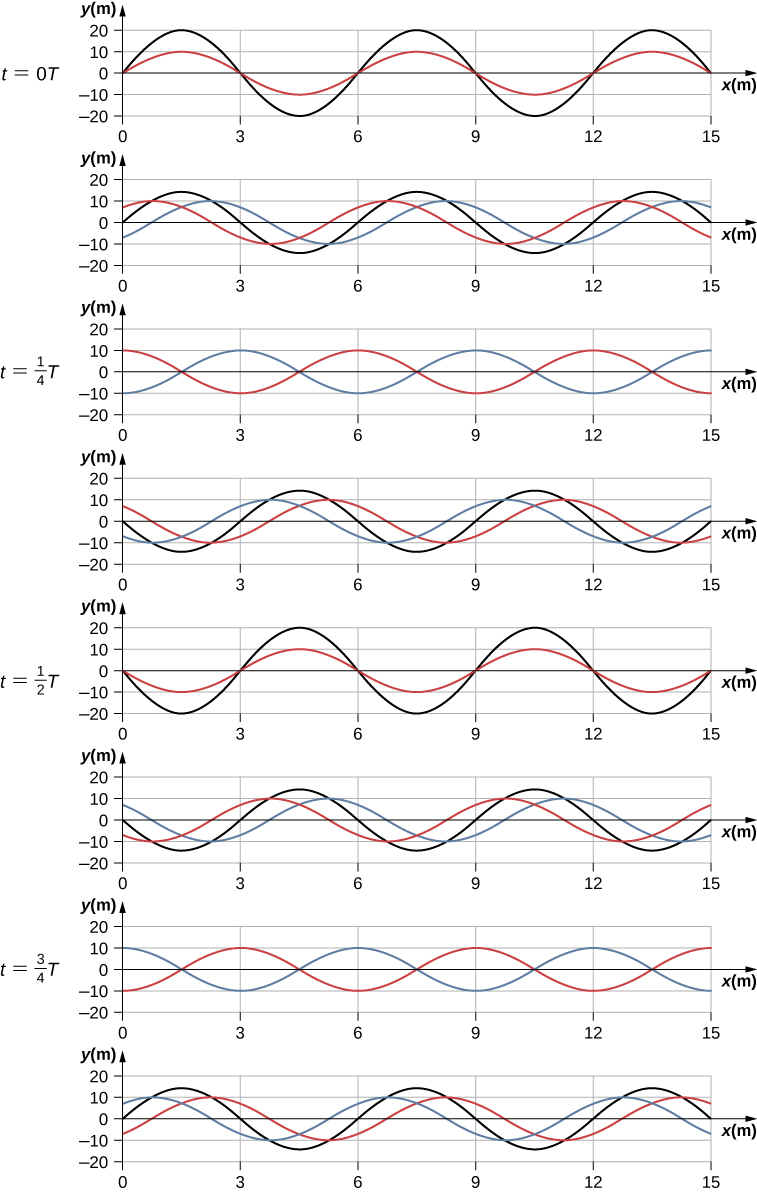
Consider two identical waves that move in opposite directions. The first wave has a wave function of [latex]{y}_{1}(x,t)=A\,\text{sin}(kx-\omega t)[/latex] and the second wave has a wave function [latex]{y}_{2}(x,t)=A\,\text{sin}(kx+\omega t)[/latex]. The waves interfere and form a resultant wave
This can be simplified using the trigonometric identity
where [latex]\alpha =kx[/latex] and [latex]\beta =\omega t[/latex], giving us
which simplifies to
Notice that the resultant wave is a sine wave that is a function only of position, multiplied by a cosine function that is a function only of time. Graphs of y(x,t) as a function of x for various times are shown in Figure. The red wave moves in the negative x-direction, the blue wave moves in the positive x-direction, and the black wave is the sum of the two waves. As the red and blue waves move through each other, they move in and out of constructive interference and destructive interference.
Initially, at time [latex]t=0,[/latex] the two waves are in phase, and the result is a wave that is twice the amplitude of the individual waves. The waves are also in phase at the time [latex]t=\frac{T}{2}.[/latex] In fact, the waves are in phase at any integer multiple of half of a period:
At other times, the two waves are [latex]180^\circ(\pi \,\text{radians})[/latex] out of phase, and the resulting wave is equal to zero. This happens at
Notice that some x-positions of the resultant wave are always zero no matter what the phase relationship is. These positions are called nodes. Where do the nodes occur? Consider the solution to the sum of the two waves
Finding the positions where the sine function equals zero provides the positions of the nodes.
There are also positions where y oscillates between [latex]y=\text{\pm}A[/latex]. These are the antinodes. We can find them by considering which values of x result in [latex]\text{sin}(kx)=\text{\pm}1[/latex].
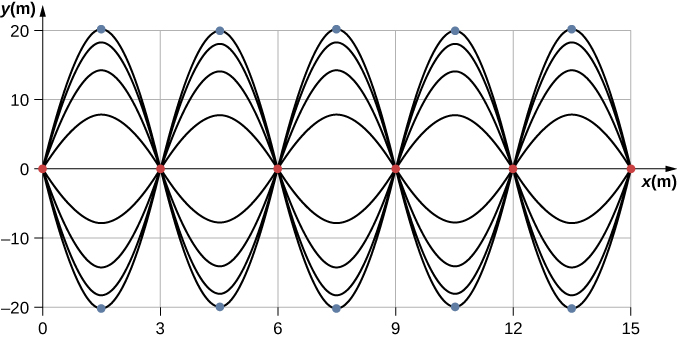
What results is a standing wave as shown in Figure, which shows snapshots of the resulting wave of two identical waves moving in opposite directions. The resulting wave appears to be a sine wave with nodes at integer multiples of half wavelengths. The antinodes oscillate between [latex]y=\text{\pm}2A[/latex] due to the cosine term, [latex]\text{cos}(\omega t)[/latex], which oscillates between [latex]\pm1[/latex].
The resultant wave appears to be standing still, with no apparent movement in the x-direction, although it is composed of one wave function moving in the positive, whereas the second wave is moving in the negative x-direction. Figure shows various snapshots of the resulting wave. The nodes are marked with red dots while the antinodes are marked with blue dots.
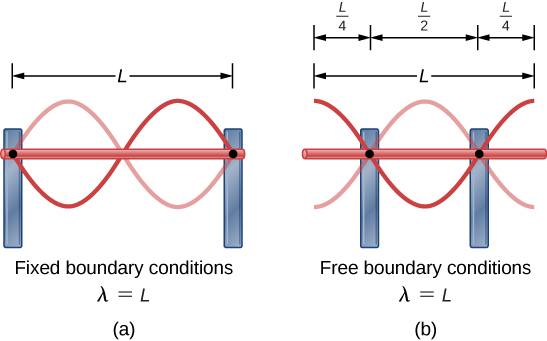
A common example of standing waves are the waves produced by stringed musical instruments. When the string is plucked, pulses travel along the string in opposite directions. The ends of the strings are fixed in place, so nodes appear at the ends of the strings—the boundary conditions of the system, regulating the resonant frequencies in the strings. The resonance produced on a string instrument can be modeled in a physics lab using the apparatus shown in Figure.
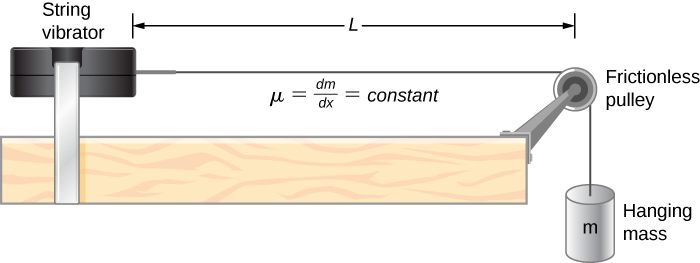
The lab setup shows a string attached to a string vibrator, which oscillates the string with an adjustable frequency f. The other end of the string passes over a frictionless pulley and is tied to a hanging mass. The magnitude of the tension in the string is equal to the weight of the hanging mass. The string has a constant linear density (mass per length) [latex]\mu[/latex] and the speed at which a wave travels down the string equals [latex]v=\sqrt{\frac{{F}_{T}}{\mu }}=\sqrt{\frac{mg}{\mu }}[/latex] Figure. The symmetrical boundary conditions (a node at each end) dictate the possible frequencies that can excite standing waves. Starting from a frequency of zero and slowly increasing the frequency, the first mode [latex]n=1[/latex] appears as shown in Figure. The first mode, also called the fundamental mode or the first harmonic, shows half of a wavelength has formed, so the wavelength is equal to twice the length between the nodes [latex]{\lambda }_{1}=2L[/latex]. The fundamental frequency, or first harmonic frequency, that drives this mode is
where the speed of the wave is [latex]v=\sqrt{\frac{{F}_{T}}{\mu }}.[/latex] Keeping the tension constant and increasing the frequency leads to the second harmonic or the [latex]n=2[/latex] mode. This mode is a full wavelength [latex]{\lambda }_{2}=L[/latex] and the frequency is twice the fundamental frequency:
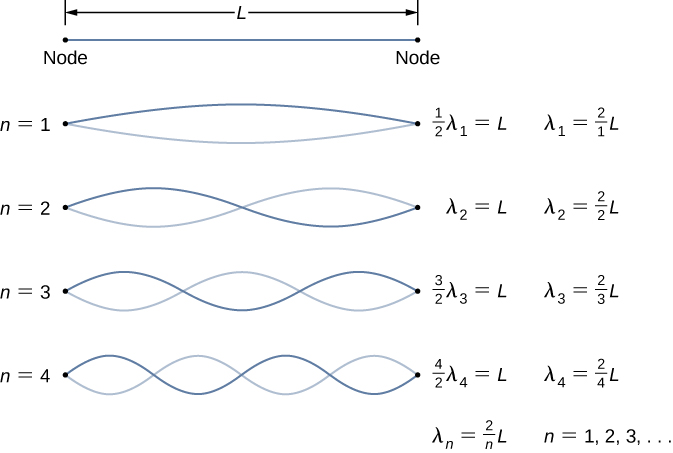
The next two modes, or the third and fourth harmonics, have wavelengths of [latex]{\lambda }_{3}=\frac{2}{3}L[/latex] and [latex]{\lambda }_{4}=\frac{2}{4}L,[/latex] driven by frequencies of [latex]{f}_{3}=\frac{3v}{2L}=3{f}_{1}[/latex] and [latex]{f}_{4}=\frac{4v}{2L}=4{f}_{1}.[/latex] All frequencies above the frequency [latex]{f}_{1}[/latex] are known as the overtones. The equations for the wavelength and the frequency can be summarized as:
The standing wave patterns that are possible for a string, the first four of which are shown in Figure, are known as the normal modes, with frequencies known as the normal frequencies. In summary, the first frequency to produce a normal mode is called the fundamental frequency (or first harmonic). Any frequencies above the fundamental frequency are overtones. The second frequency of the [latex]n=2[/latex] normal mode of the string is the first overtone (or second harmonic). The frequency of the [latex]n=3[/latex] normal mode is the second overtone (or third harmonic) and so on.
The solutions shown as (Equation) and (Equation) are for a string with the boundary condition of a node on each end. When the boundary condition on either side is the same, the system is said to have symmetric boundary conditions. (Equation) and (Equation) are good for any symmetric boundary conditions, that is, nodes at both ends or antinodes at both ends.
Example
Standing Waves on a String
Consider a string of [latex]L=2.00\,\text{m}.[/latex] attached to an adjustable-frequency string vibrator as shown in Figure. The waves produced by the vibrator travel down the string and are reflected by the fixed boundary condition at the pulley. The string, which has a linear mass density of [latex]\mu =0.006\,\text{kg/m,}[/latex] is passed over a frictionless pulley of a negligible mass, and the tension is provided by a 2.00-kg hanging mass. (a) What is the velocity of the waves on the string? (b) Draw a sketch of the first three normal modes of the standing waves that can be produced on the string and label each with the wavelength. (c) List the frequencies that the string vibrator must be tuned to in order to produce the first three normal modes of the standing waves.
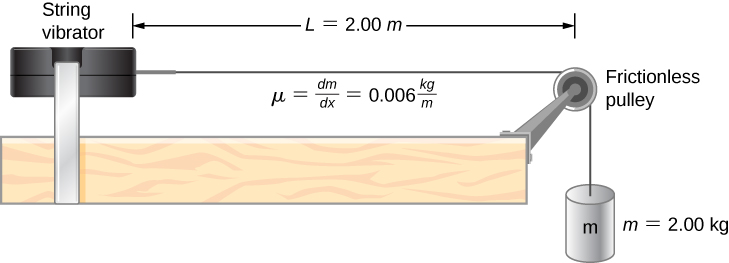
Strategy
- The velocity of the wave can be found using [latex]v=\sqrt{\frac{{F}_{T}}{\mu }}.[/latex] The tension is provided by the weight of the hanging mass.
- The standing waves will depend on the boundary conditions. There must be a node at each end. The first mode will be one half of a wave. The second can be found by adding a half wavelength. That is the shortest length that will result in a node at the boundaries. For example, adding one quarter of a wavelength will result in an antinode at the boundary and is not a mode which would satisfy the boundary conditions. This is shown in Figure.
- Since the wave speed velocity is the wavelength times the frequency, the frequency is wave speed divided by the wavelength.

Figure 16.31 (a) The figure represents the second mode of the string that satisfies the boundary conditions of a node at each end of the string. (b)This figure could not possibly be a normal mode on the string because it does not satisfy the boundary conditions. There is a node on one end, but an antinode on the other.
Solution
- Begin with the velocity of a wave on a string. The tension is equal to the weight of the hanging mass. The linear mass density and mass of the hanging mass are given:
[latex]v=\sqrt{\frac{{F}_{T}}{\mu }}=\sqrt{\frac{mg}{\mu }}=\sqrt{\frac{2\,\text{kg}(9.8\frac{\text{m}}{\text{s}})}{0.006\frac{\text{kg}}{\text{m}}}}=57.15\,\text{m/s}.[/latex]
- The first normal mode that has a node on each end is a half wavelength. The next two modes are found by adding a half of a wavelength.

- The frequencies of the first three modes are found by using [latex]f=\frac{{v}_{w}}{\lambda }.[/latex]
[latex]\begin{array}{}\\ {f}_{1}=\frac{{v}_{w}}{{\lambda }_{1}}=\frac{57.15\,\text{m/s}}{4.00\,\text{m}}=14.29\,\text{Hz}\hfill \\ {f}_{2}=\frac{{v}_{w}}{{\lambda }_{2}}=\frac{57.15\,\text{m/s}}{2.00\,\text{m}}=28.58\,\text{Hz}\hfill \\ {f}_{3}=\frac{{v}_{w}}{{\lambda }_{3}}=\frac{57.15\,\text{m/s}}{1.333\,\text{m}}=42.87\,\text{Hz}\hfill \end{array}[/latex]
Significance
The three standing modes in this example were produced by maintaining the tension in the string and adjusting the driving frequency. Keeping the tension in the string constant results in a constant velocity. The same modes could have been produced by keeping the frequency constant and adjusting the speed of the wave in the string (by changing the hanging mass.)
Visit this simulation to play with a 1D or 2D system of coupled mass-spring oscillators. Vary the number of masses, set the initial conditions, and watch the system evolve. See the spectrum of normal modes for arbitrary motion. See longitudinal or transverse modes in the 1D system.
Check Your Understanding
The equations for the wavelengths and the frequencies of the modes of a wave produced on a string:
were derived by considering a wave on a string where there were symmetric boundary conditions of a node at each end. These modes resulted from two sinusoidal waves with identical characteristics except they were moving in opposite directions, confined to a region L with nodes required at both ends. Will the same equations work if there were symmetric boundary conditions with antinodes at each end? What would the normal modes look like for a medium that was free to oscillate on each end? Don’t worry for now if you cannot imagine such a medium, just consider two sinusoidal wave functions in a region of length L, with antinodes on each end.
Yes, the equations would work equally well for symmetric boundary conditions of a medium free to oscillate on each end where there was an antinode on each end. The normal modes of the first three modes are shown below. The dotted line shows the equilibrium position of the medium.

Note that the first mode is two quarters, or one half, of a wavelength. The second mode is one quarter of a wavelength, followed by one half of a wavelength, followed by one quarter of a wavelength, or one full wavelength. The third mode is one and a half wavelengths. These are the same result as the string with a node on each end. The equations for symmetrical boundary conditions work equally well for fixed boundary conditions and free boundary conditions. These results will be revisited in the next chapter when discussing sound wave in an open tube.
The free boundary conditions shown in the last Check Your Understanding may seem hard to visualize. How can there be a system that is free to oscillate on each end? In Figure are shown two possible configuration of a metallic rods (shown in red) attached to two supports (shown in blue). In part (a), the rod is supported at the ends, and there are fixed boundary conditions at both ends. Given the proper frequency, the rod can be driven into resonance with a wavelength equal to length of the rod, with nodes at each end. In part (b), the rod is supported at positions one quarter of the length from each end of the rod, and there are free boundary conditions at both ends. Given the proper frequency, this rod can also be driven into resonance with a wavelength equal to the length of the rod, but there are antinodes at each end. If you are having trouble visualizing the wavelength in this figure, remember that the wavelength may be measured between any two nearest identical points and consider Figure.
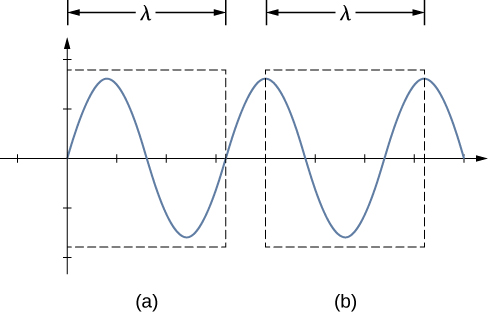
Note that the study of standing waves can become quite complex. In Figure(a), the [latex]n=2[/latex] mode of the standing wave is shown, and it results in a wavelength equal to L. In this configuration, the [latex]n=1[/latex] mode would also have been possible with a standing wave equal to 2L. Is it possible to get the [latex]n=1[/latex] mode for the configuration shown in part (b)? The answer is no. In this configuration, there are additional conditions set beyond the boundary conditions. Since the rod is mounted at a point one quarter of the length from each side, a node must exist there, and this limits the possible modes of standing waves that can be created. We leave it as an exercise for the reader to consider if other modes of standing waves are possible. It should be noted that when a system is driven at a frequency that does not cause the system to resonate, vibrations may still occur, but the amplitude of the vibrations will be much smaller than the amplitude at resonance.
A field of mechanical engineering uses the sound produced by the vibrating parts of complex mechanical systems to troubleshoot problems with the systems. Suppose a part in an automobile is resonating at the frequency of the car’s engine, causing unwanted vibrations in the automobile. This may cause the engine to fail prematurely. The engineers use microphones to record the sound produced by the engine, then use a technique called Fourier analysis to find frequencies of sound produced with large amplitudes and then look at the parts list of the automobile to find a part that would resonate at that frequency. The solution may be as simple as changing the composition of the material used or changing the length of the part in question.
There are other numerous examples of resonance in standing waves in the physical world. The air in a tube, such as found in a musical instrument like a flute, can be forced into resonance and produce a pleasant sound, as we discuss in Sound.
At other times, resonance can cause serious problems. A closer look at earthquakes provides evidence for conditions appropriate for resonance, standing waves, and constructive and destructive interference. A building may vibrate for several seconds with a driving frequency matching that of the natural frequency of vibration of the building—producing a resonance resulting in one building collapsing while neighboring buildings do not. Often, buildings of a certain height are devastated while other taller buildings remain intact. The building height matches the condition for setting up a standing wave for that particular height. The span of the roof is also important. Often it is seen that gymnasiums, supermarkets, and churches suffer damage when individual homes suffer far less damage. The roofs with large surface areas supported only at the edges resonate at the frequencies of the earthquakes, causing them to collapse. As the earthquake waves travel along the surface of Earth and reflect off denser rocks, constructive interference occurs at certain points. Often areas closer to the epicenter are not damaged, while areas farther away are damaged.
Summary
- A standing wave is the superposition of two waves which produces a wave that varies in amplitude but does not propagate.
- Nodes are points of no motion in standing waves.
- An antinode is the location of maximum amplitude of a standing wave.
- Normal modes of a wave on a string are the possible standing wave patterns. The lowest frequency that will produce a standing wave is known as the fundamental frequency. The higher frequencies which produce standing waves are called overtones.
Key Equations
| Wave speed | [latex]v=\frac{\lambda }{T}=\lambda f[/latex] |
| Linear mass density | [latex]\mu =\frac{\text{mass of the string}}{\text{length of the string}}[/latex] |
| Speed of a wave or pulse on a string under
tension |
[latex]|v|=\sqrt{\frac{{F}_{T}}{\mu }}[/latex] |
| Speed of a compression wave in a fluid | [latex]v=\sqrt{\frac{Β}{\rho }}[/latex] |
| Resultant wave from superposition of two
sinusoidal waves that are identical except for a phase shift |
[latex]{y}_{R}(x,t)=[2A\,\text{cos}(\frac{\varphi }{2})]\text{sin}(kx-\omega t+\frac{\varphi }{2})[/latex] |
| Wave number | [latex]k\equiv \frac{2\pi }{\lambda }[/latex] |
| Wave speed | [latex]v=\frac{\omega }{k}[/latex] |
| A periodic wave | [latex]y(x,t)=A\,\text{sin}(kx\mp \omega t+\varphi )[/latex] |
| Phase of a wave | [latex]kx\mp \omega t+\varphi[/latex] |
| The linear wave equation | [latex]\frac{{\partial }^{2}y(x,t)}{\partial {x}^{2}}=\frac{1}{{v}_{w}^{2}}\,\frac{{\partial }^{2}y(x,t)}{\partial {t}^{2}}[/latex] |
| Power in a wave for one wavelength | [latex]{P}_{\text{ave}}=\frac{{E}_{\lambda }}{T}=\frac{1}{2}\mu {A}^{2}{\omega }^{2}\frac{\lambda }{T}=\frac{1}{2}\mu {A}^{2}{\omega }^{2}v[/latex] |
| Intensity | [latex]I=\frac{P}{A}[/latex] |
| Intensity for a spherical wave | [latex]I=\frac{P}{4\pi {r}^{2}}[/latex] |
| Equation of a standing wave | [latex]y(x,t)=[2A\,\text{sin}(kx)]\text{cos}(\omega t)[/latex] |
| Wavelength for symmetric boundary
conditions |
[latex]{\lambda }_{n}=\frac{2}{n}L,\quad n=1,2,3,4,5\text{...}[/latex] |
| Frequency for symmetric boundary conditions | [latex]{f}_{n}=n\frac{v}{2L}=n{f}_{1},\quad n=1,2,3,4,5\text{...}[/latex] |
Conceptual Questions
A truck manufacturer finds that a strut in the engine is failing prematurely. A sound engineer determines that the strut resonates at the frequency of the engine and suspects that this could be the problem. What are two possible characteristics of the strut can be modified to correct the problem?
Show Solution
It may be as easy as changing the length and/or the density a small amount so that the parts do not resonate at the frequency of the motor.
Why do roofs of gymnasiums and churches seem to fail more than family homes when an earthquake occurs?
Wine glasses can be set into resonance by moistening your finger and rubbing it around the rim of the glass. Why?
Show Solution
Energy is supplied to the glass by the work done by the force of your finger on the glass. When supplied at the right frequency, standing waves form. The glass resonates and the vibrations produce sound.
Air conditioning units are sometimes placed on the roof of homes in the city. Occasionally, the air conditioners cause an undesirable hum throughout the upper floors of the homes. Why does this happen? What can be done to reduce the hum?
Consider a standing wave modeled as [latex]y(x,t)=4.00\,\text{cm}\,\text{sin}(3\,{\text{m}}^{-1}x)\text{cos}(4\,{\text{s}}^{-1}t).[/latex] Is there a node or an antinode at [latex]x=0.00\,\text{m}?[/latex] What about a standing wave modeled as [latex]y(x,t)=4.00\,\text{cm}\,\text{sin}(3\,{\text{m}}^{-1}x+\frac{\pi }{2})\text{cos}(4\,{\text{s}}^{-1}t)?[/latex] Is there a node or an antinode at the [latex]x=0.00\,\text{m}[/latex] position?
Show Solution
For the equation [latex]y(x,t)=4.00\,\text{cm}\,\text{sin}(3\,{\text{m}}^{-1}x)\text{cos}(4\,{\text{s}}^{-1}t),[/latex] there is a node because when [latex]x=0.00\,\text{m}[/latex], [latex]\text{sin}(3\,{\text{m}}^{-1}(0.00\,\text{m}))=0.00,[/latex] so [latex]y(0.00\,\text{m},t)=0.00\,\text{m}[/latex] for all time. For the equation [latex]y(x,t)=4.00\,\text{cm}\,\text{sin}(3\,{\text{m}}^{-1}x+\frac{\pi }{2})\text{cos}(4\,{\text{s}}^{-1}t),[/latex] there is an antinode because when [latex]x=0.00\,\text{m}[/latex], [latex]\text{sin}(3\,{\text{m}}^{-1}(0.00\,\text{m})+\frac{\pi }{2})=+1.00[/latex], so [latex]y(0.00\,\text{m},t)[/latex] oscillates between +A and −A as the cosine term oscillates between +1 and -1.
Problems
A wave traveling on a Slinky® that is stretched to 4 m takes 2.4 s to travel the length of the Slinky and back again. (a) What is the speed of the wave? (b) Using the same Slinky stretched to the same length, a standing wave is created which consists of three antinodes and four nodes. At what frequency must the Slinky be oscillating?
A 2-m long string is stretched between two supports with a tension that produces a wave speed equal to [latex]{v}_{w}=50.00\,\text{m/s}.[/latex] What are the wavelength and frequency of the first three modes that resonate on the string?
Show Solution
[latex]\begin{array}{cc} {\lambda }_{n}=\frac{2.00}{n}L,\quad {f}_{n}=\frac{v}{{\lambda }_{n}}\hfill \\ {\lambda }_{1}=4.00\,\text{m},\quad {f}_{1}=12.5\,\text{Hz}\hfill \\ {\lambda }_{2}=2.00\,\text{m},\quad {f}_{2}=25.00\,\text{Hz}\hfill \\ {\lambda }_{3}=1.33\,\text{m},\quad {f}_{3}=37.59\,\text{Hz}\hfill \end{array}[/latex]
Consider the experimental setup shown below. The length of the string between the string vibrator and the pulley is [latex]L=1.00\,\text{m}.[/latex] The linear density of the string is [latex]\mu =0.006\,\text{kg/m}.[/latex] The string vibrator can oscillate at any frequency. The hanging mass is 2.00 kg. (a)What are the wavelength and frequency of [latex]n=6[/latex] mode? (b) The string oscillates the air around the string. What is the wavelength of the sound if the speed of the sound is [latex]{v}_{s}=343.00\,\text{m/s?}[/latex]

A cable with a linear density of [latex]\mu =0.2\,\text{kg/m}[/latex] is hung from telephone poles. The tension in the cable is 500.00 N. The distance between poles is 20 meters. The wind blows across the line, causing the cable resonate. A standing waves pattern is produced that has 4.5 wavelengths between the two poles. The air temperature is [latex]T=20^\circ\text{C}.[/latex] What are the frequency and wavelength of the hum?
[latex]\begin{array}{cc} v=158.11\,\text{m/s,}\quad \lambda =4.44\,\text{m,}\quad f=35.61\,\text{Hz}\hfill \\ {\lambda }_{s}=9.63\,\text{m}\hfill \end{array}[/latex]Show Answer
Consider a rod of length L, mounted in the center to a support. A node must exist where the rod is mounted on a support, as shown below. Draw the first two normal modes of the rod as it is driven into resonance. Label the wavelength and the frequency required to drive the rod into resonance.

Consider two wave functions [latex]y(x,t)=0.30\,\text{cm}\,\text{sin}(3\,{\text{m}}^{-1}x-4\,{\text{s}}^{-1}t)[/latex] and [latex]y(x,t)=0.30\,\text{cm}\,\text{sin}(3\,{\text{m}}^{-1}x+4\,{\text{s}}^{-1}t)[/latex]. Write a wave function for the resulting standing wave.
Show Solution
[latex]y(x,t)=[0.60\,\text{cm}\,\text{sin}(3\,{\text{m}}^{-1}x)]\text{cos}(4\,{\text{s}}^{-1}t)[/latex]
A 2.40-m wire has a mass of 7.50 g and is under a tension of 160 N. The wire is held rigidly at both ends and set into oscillation. (a) What is the speed of waves on the wire? The string is driven into resonance by a frequency that produces a standing wave with a wavelength equal to 1.20 m. (b) What is the frequency used to drive the string into resonance?
A string with a linear mass density of 0.0062 kg/m and a length of 3.00 m is set into the [latex]n=100[/latex] mode of resonance. The tension in the string is 20.00 N. What is the wavelength and frequency of the wave?
Show Solution
[latex]\begin{array}{cc} {\lambda }_{100}=0.06\,\text{m}\hfill \\ \\ v=56.8\,\text{m/s,}\quad {f}_{n}=n{f}_{1},\quad n=1,2,3,4,5\text{...}\hfill \\ {f}_{100}=947\,\text{Hz}\hfill \end{array}[/latex]
A string with a linear mass density of 0.0075 kg/m and a length of 6.00 m is set into the [latex]n=4[/latex] mode of resonance by driving with a frequency of 100.00 Hz. What is the tension in the string?
Two sinusoidal waves with identical wavelengths and amplitudes travel in opposite directions along a string producing a standing wave. The linear mass density of the string is [latex]\mu =0.075\,\text{kg/m}[/latex] and the tension in the string is [latex]{F}_{T}=5.00\,\text{N}.[/latex] The time interval between instances of total destructive interference is [latex]\Delta t=0.13\,\text{s}.[/latex] What is the wavelength of the waves?
Show Solution
[latex]T=2\Delta t,\quad v=\frac{\lambda }{T},\quad \lambda =2.12\,\text{m}[/latex]
A string, fixed on both ends, is 5.00 m long and has a mass of 0.15 kg. The tension if the string is 90 N. The string is vibrating to produce a standing wave at the fundamental frequency of the string. (a) What is the speed of the waves on the string? (b) What is the wavelength of the standing wave produced? (c) What is the period of the standing wave?
A string is fixed at both end. The mass of the string is 0.0090 kg and the length is 3.00 m. The string is under a tension of 200.00 N. The string is driven by a variable frequency source to produce standing waves on the string. Find the wavelengths and frequency of the first four modes of standing waves.
Show Solution
[latex]\begin{array}{cc} {\lambda }_{1}=6.00\,\text{m},\quad {\lambda }_{2}=3.00\,\text{m},\quad {\lambda }_{3}=2.00\,\text{m},\quad {\lambda }_{4}=1.50\,\text{m}\hfill \\ v=258.20\,\text{m/s}=\lambda f\hfill \\ {f}_{1}=43.03\,\text{Hz},\quad {f}_{2}=86.07\,\text{Hz},\quad {f}_{3}=129.10\,\text{Hz},\quad {f}_{4}=172.13\,\text{Hz}\hfill \end{array}[/latex]
The frequencies of two successive modes of standing waves on a string are 258.36 Hz and 301.42 Hz. What is the next frequency above 100.00 Hz that would produce a standing wave?
A string is fixed at both ends to supports 3.50 m apart and has a linear mass density of [latex]\mu =0.005\,\text{kg/m}.[/latex] The string is under a tension of 90.00 N. A standing wave is produced on the string with six nodes and five antinodes. What are the wave speed, wavelength, frequency, and period of the standing wave?
Show Solution
[latex]v=134.16\,\text{ms},\lambda =1.4\,\text{m},f=95.83\,\text{Hz},T=0.0104\,\text{s}[/latex]
Sine waves are sent down a 1.5-m-long string fixed at both ends. The waves reflect back in the opposite direction. The amplitude of the wave is 4.00 cm. The propagation velocity of the waves is 175 m/s. The [latex]n=6[/latex] resonance mode of the string is produced. Write an equation for the resulting standing wave.
Additional Problems
Ultrasound equipment used in the medical profession uses sound waves of a frequency above the range of human hearing. If the frequency of the sound produced by the ultrasound machine is [latex]f=30\,\text{kHz,}[/latex] what is the wavelength of the ultrasound in bone, if the speed of sound in bone is [latex]v=3000\,\text{m/s?}[/latex]
Show Solution
[latex]\lambda =0.10\,\text{m}[/latex]
Shown below is the plot of a wave function that models a wave at time [latex]t=0.00\,\text{s}[/latex] and [latex]t=2.00\,\text{s}[/latex]. The dotted line is the wave function at time [latex]t=0.00\,\text{s}[/latex] and the solid line is the function at time [latex]t=2.00\,\text{s}[/latex]. Estimate the amplitude, wavelength, velocity, and period of the wave.

The speed of light in air is approximately [latex]v=3.00\times {10}^{8}\,\text{m/s}[/latex] and the speed of light in glass is [latex]v=2.00\times {10}^{8}\,\text{m/s}[/latex]. A red laser with a wavelength of [latex]\lambda =633.00\,\text{nm}[/latex] shines light incident of the glass, and some of the red light is transmitted to the glass. The frequency of the light is the same for the air and the glass. (a) What is the frequency of the light? (b) What is the wavelength of the light in the glass?
Show Solution
a. [latex]f=4.74\times {10}^{14}\,\text{Hz;}[/latex] b. [latex]\lambda =422\,\text{nm}[/latex]
A radio station broadcasts radio waves at a frequency of 101.7 MHz. The radio waves move through the air at approximately the speed of light in a vacuum. What is the wavelength of the radio waves?
A sunbather stands waist deep in the ocean and observes that six crests of periodic surface waves pass each minute. The crests are 16.00 meters apart. What is the wavelength, frequency, period, and speed of the waves?
Show Solution
[latex]\lambda =16.00\,\text{m},\quad f=0.10\,\text{Hz},\quad T=10.00\,\text{s},\quad v=1.6\,\text{m/s}[/latex]
A tuning fork vibrates producing sound at a frequency of 512 Hz. The speed of sound of sound in air is [latex]v=343.00\,\text{m/s}[/latex] if the air is at a temperature of [latex]20.00^\circ\text{C}[/latex]. What is the wavelength of the sound?
A motorboat is traveling across a lake at a speed of [latex]{v}_{b}=15.00\,\text{m/s}.[/latex] The boat bounces up and down every 0.50 s as it travels in the same direction as a wave. It bounces up and down every 0.30 s as it travels in a direction opposite the direction of the waves. What is the speed and wavelength of the wave?
Show Solution
[latex]\lambda =({v}_{b}+v){t}_{b},\quad v=3.75\,\text{m/s,}\quad \lambda =3.00\,\text{m}[/latex]
Use the linear wave equation to show that the wave speed of a wave modeled with the wave function [latex]y(x,t)=0.20\,\text{m}\,\text{sin}(3.00\,{\text{m}}^{-1}x+6.00\,{\text{s}}^{-1}t)[/latex] is [latex]v=2.00\,\text{m/s}.[/latex] What are the wavelength and the speed of the wave?
Given the wave functions [latex]{y}_{1}(x,t)=A\,\text{sin}(kx-\omega t)[/latex] and [latex]{y}_{2}(x,t)=A\,\text{sin}(kx-\omega t+\varphi )[/latex] with [latex]\varphi \ne \frac{\pi }{2}[/latex], show that [latex]{y}_{1}(x,t)+{y}_{2}(x,t)[/latex] is a solution to the linear wave equation with a wave velocity of [latex]v=\sqrt{\frac{\omega }{k}}.[/latex]
Show Solution
[latex]\begin{array}{cc} \frac{{\partial }^{2}({y}_{1}+{y}_{2})}{\partial {t}^{2}}=\text{−}A{\omega }^{2}\,\text{sin}(kx-\omega t)-A{\omega }^{2}\,\text{sin}(kx-\omega t+\varphi )\hfill \\ \frac{{\partial }^{2}({y}_{1}+{y}_{2})}{\partial {x}^{2}}=\text{−}A{k}^{2}\,\text{sin}(kx-\omega t)-A{k}^{2}\,\text{sin}(kx-\omega t+\varphi )\hfill \\ \frac{{\partial }^{2}y(x,t)}{\partial {x}^{2}}=\frac{1}{{v}^{2}}\,\frac{{\partial }^{2}y(x,t)}{\partial {t}^{2}}\hfill \\ \\ -A{\omega }^{2}\,\text{sin}(kx-\omega t)-A{\omega }^{2}\,\text{sin}(kx-\omega t+\varphi )=(\frac{1}{{v}^{2}})(\text{−}A{k}^{2}\,\text{sin}(kx-\omega t)-A{k}^{2}\,\text{sin}(kx-\omega t+\varphi ))\hfill \\ v=\frac{\omega }{k}\hfill \end{array}[/latex]
A transverse wave on a string is modeled with the wave function [latex]y(x,t)=0.10\,\text{m}\,\text{sin}(0.15\,{\text{m}}^{-1}x+1.50\,{\text{s}}^{-1}t+0.20)[/latex]. (a) Find the wave velocity. (b) Find the position in the y-direction, the velocity perpendicular to the motion of the wave, and the acceleration perpendicular to the motion of the wave, of a small segment of the string centered at [latex]x=0.40\,\text{m}[/latex] at time [latex]t=5.00\,\text{s}.[/latex]
A sinusoidal wave travels down a taut, horizontal string with a linear mass density of [latex]\mu =0.060\,\text{kg/m}.[/latex] The magnitude of maximum vertical acceleration of the wave is [latex]{a}_{y\,\text{max}}=0.90\,{\text{cm/s}}^{2}[/latex] and the amplitude of the wave is 0.40 m. The string is under a tension of [latex]{F}_{T}=600.00\,\text{N}[/latex]. The wave moves in the negative x-direction. Write an equation to model the wave.
Show Solution
[latex]y(x,t)=0.40\,\text{m}\,\text{sin}(0.015\,{\text{m}}^{-1}x+1.5\,{\text{s}}^{-1}t)[/latex]
A transverse wave on a string [latex](\mu =0.0030\,\text{kg/m})[/latex] is described with the equation [latex]y(x,t)=0.30\,\text{m}\,\text{sin}(\frac{2\pi }{4.00\,\text{m}}(x-16.00\frac{\text{m}}{\text{s}}t)).[/latex] What is the tension under which the string is held taut?
A transverse wave on a horizontal string [latex](\mu =0.0060\,\text{kg/m})[/latex] is described with the equation [latex]y(x,t)=0.30\,\text{m}\,\text{sin}(\frac{2\pi }{4.00\,\text{m}}(x-{v}_{w}t)).[/latex] The string is under a tension of 300.00 N. What are the wave speed, wave number, and angular frequency of the wave?
Show Solution
[latex]v=223.61\,\text{m/s},\,k=1.57\,{\text{m}}^{-1},\,\omega =142.43\,{\text{s}}^{-1}[/latex]
A student holds an inexpensive sonic range finder and uses the range finder to find the distance to the wall. The sonic range finder emits a sound wave. The sound wave reflects off the wall and returns to the range finder. The round trip takes 0.012 s. The range finder was calibrated for use at room temperature [latex]T=20^\circ\text{C}[/latex], but the temperature in the room is actually [latex]T=23^\circ\text{C}.[/latex] Assuming that the timing mechanism is perfect, what percentage of error can the student expect due to the calibration?
A wave on a string is driven by a string vibrator, which oscillates at a frequency of 100.00 Hz and an amplitude of 1.00 cm. The string vibrator operates at a voltage of 12.00 V and a current of 0.20 A. The power consumed by the string vibrator is [latex]P=IV[/latex]. Assume that the string vibrator is [latex]90\text{%}[/latex] efficient at converting electrical energy into the energy associated with the vibrations of the string. The string is 3.00 m long, and is under a tension of 60.00 N. What is the linear mass density of the string?
Show Solution
[latex]\begin{array}{cc} P=\frac{1}{2}{A}^{2}{(2\pi f)}^{2}\sqrt{\mu {F}_{T}}\hfill \\ \mu =2.00\times {10}^{-4}\,\text{kg/m}\hfill \end{array}[/latex]
A traveling wave on a string is modeled by the wave equation [latex]y(x,t)=3.00\,\text{cm}\,\text{sin}(8.00\,{\text{m}}^{-1}x+100.00\,{\text{s}}^{-1}t).[/latex] The string is under a tension of 50.00 N and has a linear mass density of [latex]\mu =0.008\,\text{kg/m}.[/latex] What is the average power transferred by the wave on the string?
A transverse wave on a string has a wavelength of 5.0 m, a period of 0.02 s, and an amplitude of 1.5 cm. The average power transferred by the wave is 5.00 W. What is the tension in the string?
Show Solution
[latex]P=\frac{1}{2}\mu {A}^{2}{\omega }^{2}\frac{\lambda }{T},\,\mu =0.0018\,\text{kg/m}[/latex]
(a) What is the intensity of a laser beam used to burn away cancerous tissue that, when [latex]90.0\text{%}[/latex] absorbed, puts 500 J of energy into a circular spot 2.00 mm in diameter in 4.00 s? (b) Discuss how this intensity compares to the average intensity of sunlight (about) and the implications that would have if the laser beam entered your eye. Note how your answer depends on the time duration of the exposure.
Consider two periodic wave functions, [latex]{y}_{1}(x,t)=A\,\text{sin}(kx-\omega t)[/latex] and [latex]{y}_{2}(x,t)=A\,\text{sin}(kx-\omega t+\varphi ).[/latex] (a) For what values of [latex]\varphi[/latex] will the wave that results from a superposition of the wave functions have an amplitude of 2A? (b) For what values of [latex]\varphi[/latex] will the wave that results from a superposition of the wave functions have an amplitude of zero?
Show Solution
a. [latex]{A}_{R}=2A\,\text{cos}(\frac{\varphi }{2}),\,\text{cos}(\frac{\varphi }{2})=1,\,\varphi =0,2\pi ,4\pi \text{,...}[/latex]; b. [latex]{A}_{R}=2A\,\text{cos}(\frac{\varphi }{2}),\,\text{cos}(\frac{\varphi }{2})=0,\,\varphi =0,\pi ,3\pi ,5\pi \text{...}[/latex]
Consider two periodic wave functions, [latex]{y}_{1}(x,t)=A\,\text{sin}(kx-\omega t)[/latex] and [latex]{y}_{2}(x,t)=A\,\text{cos}(kx-\omega t+\varphi )[/latex]. (a) For what values of [latex]\varphi[/latex] will the wave that results from a superposition of the wave functions have an amplitude of 2A? (b) For what values of [latex]\varphi[/latex] will the wave that results from a superposition of the wave functions have an amplitude of zero?
A trough with dimensions 10.00 meters by 0.10 meters by 0.10 meters is partially filled with water. Small-amplitude surface water waves are produced from both ends of the trough by paddles oscillating in simple harmonic motion. The height of the water waves are modeled with two sinusoidal wave equations, [latex]{y}_{1}(x,t)=0.3\,\text{m}\,\text{sin}(4\,{\text{m}}^{-1}x-3\,{\text{s}}^{-1}t)[/latex] and [latex]{y}_{2}(x,t)=0.3\,\text{m}\,\text{cos}(4\,{\text{m}}^{-1}x+3\,{\text{s}}^{-1}t-\frac{\pi }{2}).[/latex] What is the wave function of the resulting wave after the waves reach one another and before they reach the end of the trough (i.e., assume that there are only two waves in the trough and ignore reflections)? Use a spreadsheet to check your results. (Hint: Use the trig identities [latex]\text{sin}(u\pm v)=\text{sin}\,u\,\text{cos}\,v\pm\text{cos}\,u\,\text{sin}\,v[/latex] and [latex]\text{cos}(u\pm v)=\text{cos}\,u\,\text{cos}\,v\mp \text{sin}\,u\,\text{sin}\,v)[/latex]
Show Solution
[latex]{y}_{R}(x,t)=0.6\,\text{m}\,\text{sin}(4\,{\text{m}}^{-1}x)\text{cos}(3\,{\text{s}}^{-1}t)[/latex]
A seismograph records the S- and P-waves from an earthquake 20.00 s apart. If they traveled the same path at constant wave speeds of [latex]{v}_{S}=4.00\,\text{km/s}[/latex] and [latex]{v}_{P}=7.50\,\text{km/s},[/latex] how far away is the epicenter of the earthquake?
Consider what is shown below. A 20.00-kg mass rests on a frictionless ramp inclined at [latex]45^\circ[/latex]. A string with a linear mass density of [latex]\mu =0.025\,\text{kg/m}[/latex] is attached to the 20.00-kg mass. The string passes over a frictionless pulley of negligible mass and is attached to a hanging mass (m). The system is in static equilibrium. A wave is induced on the string and travels up the ramp. (a) What is the mass of the hanging mass (m)? (b) At what wave speed does the wave travel up the string?

a. [latex]\begin{array}{cc} (1){F}_{T}-20.00\,\text{kg}(9.80\,{\text{m/s}}^{2})\text{cos}\,45^\circ=0\hfill \\ (2)m(9.80\,{\text{m/s}}^{2})-{F}_{T}=0\hfill \\ m=14.14\,\text{kg}\hfill \end{array}[/latex]; b. [latex]\begin{array}{cc} \hfill {F}_{T}& =\hfill & 138.57\,\text{N}\hfill \\ \hfill v& =\hfill & 67.96\,\text{m/s}\hfill \end{array}[/latex]Show Answer
Consider the superposition of three wave functions [latex]y(x,t)=3.00\,\text{cm}\,\text{sin}(2\,{\text{m}}^{-1}x-3\,{\text{s}}^{-1}t),[/latex] [latex]y(x,t)=3.00\,\text{cm}\,\text{sin}(6\,{\text{m}}^{-1}x+3\,{\text{s}}^{-1}t),[/latex] and [latex]y(x,t)=3.00\,\text{cm}\,\text{sin}(2\,{\text{m}}^{-1}x-4\,{\text{s}}^{-1}t).[/latex] What is the height of the resulting wave at position [latex]x=3.00\,\text{m}[/latex] at time [latex]t=10.0\,\text{s?}[/latex]
A string has a mass of 150 g and a length of 3.4 m. One end of the string is fixed to a lab stand and the other is attached to a spring with a spring constant of [latex]{k}_{s}=100\,\text{N/m}.[/latex] The free end of the spring is attached to another lab pole. The tension in the string is maintained by the spring. The lab poles are separated by a distance that stretches the spring 2.00 cm. The string is plucked and a pulse travels along the string. What is the propagation speed of the pulse?
Show Solution
[latex]{F}_{T}=12\,\text{N,}\,v=16.49\,\text{m/s}[/latex]
A standing wave is produced on a string under a tension of 70.0 N by two sinusoidal transverse waves that are identical, but moving in opposite directions. The string is fixed at [latex]x=0.00\,\text{m}[/latex] and [latex]x=10.00\,\text{m}.[/latex] Nodes appear at [latex]x=0.00\,\text{m,}[/latex] 2.00 m, 4.00 m, 6.00 m, 8.00 m, and 10.00 m. The amplitude of the standing wave is 3.00 cm. It takes 0.10 s for the antinodes to make one complete oscillation. (a) What are the wave functions of the two sine waves that produce the standing wave? (b) What are the maximum velocity and acceleration of the string, perpendicular to the direction of motion of the transverse waves, at the antinodes?
A string with a length of 4 m is held under a constant tension. The string has a linear mass density of [latex]\mu =0.006\,\text{kg/m}.[/latex] Two resonant frequencies of the string are 400 Hz and 480 Hz. There are no resonant frequencies between the two frequencies. (a) What are the wavelengths of the two resonant modes? (b) What is the tension in the string?
Show Solution
a. [latex]\begin{array}{cc} {f}_{n}=\frac{nv}{2L},\,v=\frac{2L{f}_{n+1}}{n+1},\,\frac{n+1}{n}=\frac{2L{f}_{n+1}}{2L{f}_{n}},\,1+\frac{1}{n}=1.2,\,n=5\hfill \\ {\lambda }_{n}=\frac{2}{n}L,\,{\lambda }_{5}=1.6\,\text{m},\,{\lambda }_{6}=1.33\,\text{m}\hfill \end{array}[/latex]; b. [latex]{F}_{T}=245.76\,\text{N}[/latex]
Challenge Problems
A copper wire has a radius of [latex]200\,\text{μm}[/latex] and a length of 5.0 m. The wire is placed under a tension of 3000 N and the wire stretches by a small amount. The wire is plucked and a pulse travels down the wire. What is the propagation speed of the pulse? (Assume the temperature does not change: [latex](\rho =8.96\frac{\text{g}}{{\text{cm}}^{3}},Y=1.1\times {10}^{11}\frac{\text{N}}{\text{m}}).)[/latex]
A pulse moving along the x axis can be modeled as the wave function [latex]y(x,t)=4.00\,\text{m}{e}^{\text{−}{(\frac{x+(2.00\,\text{m/s})t}{1.00\,\text{m}})}^{2}}.[/latex] (a)What are the direction and propagation speed of the pulse? (b) How far has the wave moved in 3.00 s? (c) Plot the pulse using a spreadsheet at time [latex]t=0.00\,\text{s}[/latex] and [latex]t=3.00\,\text{s}[/latex] to verify your answer in part (b).
Show Solution
a. Moves in the negative x direction at a propagation speed of [latex]v=2.00\,\text{m/s}[/latex]. b. [latex]\Delta x=-6.00\,\text{m;}[/latex] c.

A string with a linear mass density of [latex]\mu =0.0085\,\text{kg/m}[/latex] is fixed at both ends. A 5.0-kg mass is hung from the string, as shown below. If a pulse is sent along section A, what is the wave speed in section A and the wave speed in section B?

Consider two wave functions [latex]{y}_{1}(x,t)=A\,\text{sin}(kx-\omega t)[/latex] and [latex]{y}_{2}(x,t)=A\,\text{sin}(kx+\omega t+\varphi )[/latex]. What is the wave function resulting from the interference of the two wave? (Hint: [latex]\text{sin}(\alpha \pm\beta )=\text{sin}\,\alpha \,\text{cos}\,\beta \pm\text{cos}\,\alpha \,\text{sin}\,\beta[/latex] and [latex]\varphi =\frac{\varphi }{2}+\frac{\varphi }{2}[/latex].)
Show Solution
[latex]\begin{array}{cc} \text{sin}(kx-\omega t)=\text{sin}(kx+\frac{\varphi }{2})\text{cos}(\omega t+\frac{\varphi }{2})-\text{cos}(kx+\frac{\varphi }{2})\text{sin}(\omega t+\frac{\varphi }{2})\hfill \\ \text{sin}(kx-\omega t+\varphi )=\text{sin}(kx+\frac{\varphi }{2})\text{cos}(\omega t+\frac{\varphi }{2})+\text{cos}(kx+\frac{\varphi }{2})\text{sin}(\omega t+\frac{\varphi }{2})\hfill \\ \text{sin}(kx-\omega t)+\text{sin}(kx+\omega t+\varphi )=2\,\text{sin}(kx+\frac{\varphi }{2})\text{cos}(\omega t+\frac{\varphi }{2})\hfill \\ {y}_{R}=2\,A\,\text{sin}(kx+\frac{\varphi }{2})\text{cos}(\omega t+\frac{\varphi }{2})\hfill \end{array}[/latex]
The wave function that models a standing wave is given as [latex]{y}_{R}(x,t)=6.00\,\text{cm}\,\text{sin}(3.00\,{\text{m}}^{-1}x+1.20\,\text{rad})[/latex] [latex]\text{cos}(6.00\,{\text{s}}^{-1}t+1.20\,\text{rad})[/latex]. What are two wave functions that interfere to form this wave function? Plot the two wave functions and the sum of the sum of the two wave functions at [latex]t=1.00\,\text{s}[/latex] to verify your answer.
Consider two wave functions [latex]{y}_{1}(x,t)=A\,\text{sin}(kx-\omega t)[/latex] and [latex]{y}_{2}(x,t)=A\,\text{sin}(kx+\omega t+\varphi )[/latex]. The resultant wave form when you add the two functions is [latex]{y}_{R}=2A\,\text{sin}(kx+\frac{\varphi }{2})\text{cos}(\omega t+\frac{\varphi }{2}).[/latex] Consider the case where [latex]A=0.03\,{\text{m}}^{-1},[/latex] [latex]k=1.26\,{\text{m}}^{-1},[/latex] [latex]\omega =\pi \,{\text{s}}^{-1}[/latex], and [latex]\varphi =\frac{\pi }{10}[/latex]. (a) Where are the first three nodes of the standing wave function starting at zero and moving in the positive x direction? (b) Using a spreadsheet, plot the two wave functions and the resulting function at time [latex]t=1.00\,\text{s}[/latex] to verify your answer.
Show Solution
[latex]\begin{array}{cc} \text{sin}(kx+\frac{\varphi }{2})=0,\,kx+\frac{\varphi }{2}=0,\pi ,2\pi ,\,1.26\,{\text{m}}^{-1}x+\frac{\pi }{20}=\pi ,2\pi ,3\pi \hfill \\ x=2.37\,\text{m},4.86\,\text{m},7.35\,\text{m}\hfill \end{array}[/latex];

Glossary
- antinode
- location of maximum amplitude in standing waves
- fundamental frequency
- lowest frequency that will produce a standing wave
- node
- point where the string does not move; more generally, nodes are where the wave disturbance is zero in a standing wave
- normal mode
- possible standing wave pattern for a standing wave on a string
- overtone
- frequency that produces standing waves and is higher than the fundamental frequency
- standing wave
- wave that can bounce back and forth through a particular region, effectively becoming stationary
