16.1 Traveling Waves

Types of Waves

A wave is a disturbance that propagates, or moves from the place it was created. There are three basic types of waves: mechanical waves, electromagnetic waves, and matter waves.

Basic mechanical waves are governed by Newton’s laws and require a medium. A medium is the substance a mechanical waves propagates through, and the medium produces an elastic restoring force when it is deformed. Mechanical waves transfer energy and momentum, without transferring mass. Some examples of mechanical waves are water waves, sound waves, and seismic waves. The medium for water waves is water; for sound waves, the medium is usually air. (Sound waves can travel in other media as well; we will look at that in more detail in Sound.) For surface water waves, the disturbance occurs on the surface of the water, perhaps created by a rock thrown into a pond or by a swimmer splashing the surface repeatedly. For sound waves, the disturbance is a change in air pressure, perhaps created by the oscillating cone inside a speaker or a vibrating tuning fork. In both cases, the disturbance is the oscillation of the molecules of the fluid. In mechanical waves, energy and momentum transfer with the motion of the wave, whereas the mass oscillates around an equilibrium point. (We discuss this in Energy and Power of a Wave.) Earthquakes generate seismic waves from several types of disturbances, including the disturbance of Earth’s surface and pressure disturbances under the surface. Seismic waves travel through the solids and liquids that form Earth. In this chapter, we focus on mechanical waves.

Electromagnetic waves are associated with oscillations in electric and magnetic fields and do not require a medium. Examples include gamma rays, X-rays, ultraviolet waves, visible light, infrared waves, microwaves, and radio waves. Electromagnetic waves can travel through a vacuum at the speed of light, [latex]v=c=2.99792458\times {10}^{8}\,\text{m/s}.[/latex] For example, light from distant stars travels through the vacuum of space and reaches Earth. Electromagnetic waves have some characteristics that are similar to mechanical waves; they are covered in more detail in Electromagnetic Waves in volume 2 of this text.

Matter waves are a central part of the branch of physics known as quantum mechanics. These waves are associated with protons, electrons, neutrons, and other fundamental particles found in nature. The theory that all types of matter have wave-like properties was first proposed by Louis de Broglie in 1924. Matter waves are discussed in Photons and Matter Waves in the third volume of this text.

Mechanical Waves

Mechanical waves exhibit characteristics common to all waves, such as amplitude, wavelength, period, frequency, and energy. All wave characteristics can be described by a small set of underlying principles.

The simplest mechanical waves repeat themselves for several cycles and are associated with simple harmonic motion. These simple harmonic waves can be modeled using some combination of sine and cosine functions. For example, consider the simplified surface water wave that moves across the surface of water as illustrated in Figure. Unlike complex ocean waves, in surface water waves, the medium, in this case water, moves vertically, oscillating up and down, whereas the disturbance of the wave moves horizontally through the medium. In Figure, the waves causes a seagull to move up and down in simple harmonic motion as the wave crests and troughs (peaks and valleys) pass under the bird. The crest is the highest point of the wave, and the trough is the lowest part of the wave. The time for one complete oscillation of the up-and-down motion is the wave’s period T. The wave’s frequency is the number of waves that pass through a point per unit time and is equal to [latex]f=1\text{/}T.[/latex] The period can be expressed using any convenient unit of time but is usually measured in seconds; frequency is usually measured in hertz (Hz), where [latex]1\,{\text{Hz}=1\,\text{s}}^{-1}.[/latex]

The length of the wave is called the wavelength and is represented by the Greek letter lambda [latex](\lambda )[/latex], which is measured in any convenient unit of length, such as a centimeter or meter. The wavelength can be measured between any two similar points along the medium that have the same height and the same slope. In Figure, the wavelength is shown measured between two crests. As stated above, the period of the wave is equal to the time for one oscillation, but it is also equal to the time for one wavelength to pass through a point along the wave’s path.

The amplitude of the wave (A) is a measure of the maximum displacement of the medium from its equilibrium position. In the figure, the equilibrium position is indicated by the dotted line, which is the height of the water if there were no waves moving through it. In this case, the wave is symmetrical, the crest of the wave is a distance [latex]\text{+}A[/latex] above the equilibrium position, and the trough is a distance [latex]\text{−}A[/latex] below the equilibrium position. The units for the amplitude can be centimeters or meters, or any convenient unit of distance.

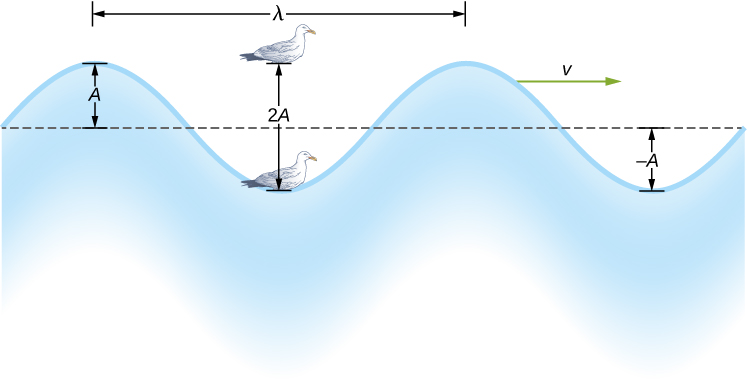
The water wave in the figure moves through the medium with a propagation velocity [latex]\mathbf{\overset{\to }{v}}.[/latex] The magnitude of the wave velocity is the distance the wave travels in a given time, which is one wavelength in the time of one period, and the wave speed is the magnitude of wave velocity. In equation form, this is

This fundamental relationship holds for all types of waves. For water waves, v is the speed of a surface wave; for sound, v is the speed of sound; and for visible light, v is the speed of light.

Transverse and Longitudinal Waves

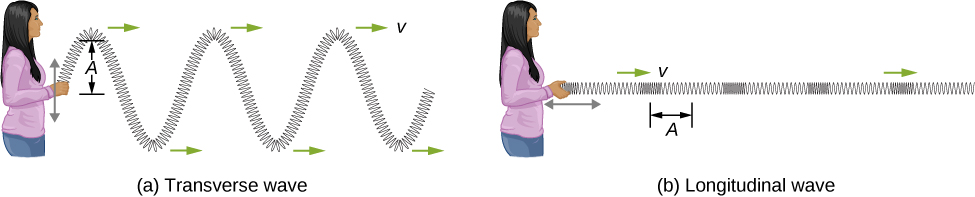
We have seen that a simple mechanical wave consists of a periodic disturbance that propagates from one place to another through a medium. In Figure(a), the wave propagates in the horizontal direction, whereas the medium is disturbed in the vertical direction. Such a wave is called a transverse wave. In a transverse wave, the wave may propagate in any direction, but the disturbance of the medium is perpendicular to the direction of propagation. In contrast, in a longitudinal wave or compressional wave, the disturbance is parallel to the direction of propagation. Figure(b) shows an example of a longitudinal wave. The size of the disturbance is its amplitude A and is completely independent of the speed of propagation v.

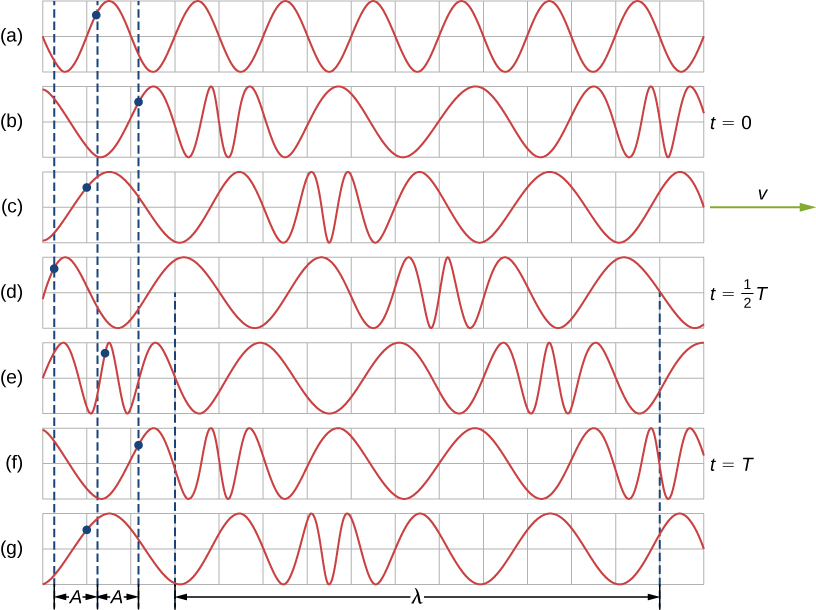
A simple graphical representation of a section of the spring shown in Figure(b) is shown in Figure. Figure(a) shows the equilibrium position of the spring before any waves move down it. A point on the spring is marked with a blue dot. Figure(b) through (g) show snapshots of the spring taken one-quarter of a period apart, sometime after the end of` the spring is oscillated back and forth in the x-direction at a constant frequency. The disturbance of the wave is seen as the compressions and the expansions of the spring. Note that the blue dot oscillates around its equilibrium position a distance A, as the longitudinal wave moves in the positive x-direction with a constant speed. The distance A is the amplitude of the wave. The y-position of the dot does not change as the wave moves through the spring. The wavelength of the wave is measured in part (d). The wavelength depends on the speed of the wave and the frequency of the driving force.

Waves may be transverse, longitudinal, or a combination of the two. Examples of transverse waves are the waves on stringed instruments or surface waves on water, such as ripples moving on a pond. Sound waves in air and water are longitudinal. With sound waves, the disturbances are periodic variations in pressure that are transmitted in fluids. Fluids do not have appreciable shear strength, and for this reason, the sound waves in them are longitudinal waves. Sound in solids can have both longitudinal and transverse components, such as those in a seismic wave. Earthquakes generate seismic waves under Earth’s surface with both longitudinal and transverse components (called compressional or P-waves and shear or S-waves, respectively). The components of seismic waves have important individual characteristics—they propagate at different speeds, for example. Earthquakes also have surface waves that are similar to surface waves on water. Ocean waves also have both transverse and longitudinal components.

Example

Characteristics of a Wave

A transverse mechanical wave propagates in the positive x-direction through a spring (as shown in Figure(a)) with a constant wave speed, and the medium oscillates between [latex]\text{+}A[/latex] and [latex]\text{−}A[/latex] around an equilibrium position. The graph in Figure shows the height of the spring (y) versus the position (x), where the x-axis points in the direction of propagation. The figure shows the height of the spring versus the x-position at [latex]t=0.00\,\text{s}[/latex] as a dotted line and the wave at [latex]t=3.00\,\text{s}[/latex] as a solid line. (a) Determine the wavelength and amplitude of the wave. (b) Find the propagation velocity of the wave. (c) Calculate the period and frequency of the wave.

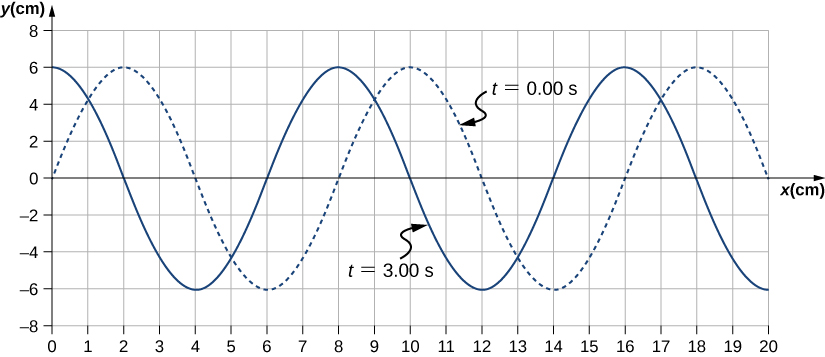
Strategy

1. The amplitude and wavelength can be determined from the graph.
2. Since the velocity is constant, the velocity of the wave can be found by dividing the distance traveled by the wave by the time it took the wave to travel the distance.
3. The period can be found from [latex]v=\frac{\lambda }{T}[/latex] and the frequency from [latex]f=\frac{1}{T}.[/latex]

Solution

1. Read the wavelength from the graph, looking at the purple arrow in Figure. Read the amplitude by looking at the green arrow. The wavelength is [latex]\lambda =8.00\,\text{cm}[/latex] and the amplitude is [latex]A=6.00\,\text{cm}.[/latex]

   

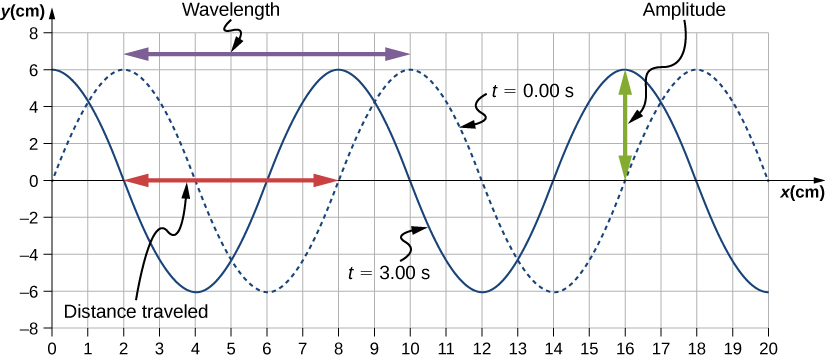
2. The distance the wave traveled from time [latex]t=0.00\,\text{s}[/latex] to time [latex]t=3.00\,\text{s}[/latex] can be seen in the graph. Consider the red arrow, which shows the distance the crest has moved in 3 s. The distance is [latex]8.00\,\text{cm}-2.00\,\text{cm}=6.00\,\text{cm}.[/latex] The velocity is
   [latex]v=\frac{\Delta x}{\Delta t}=\frac{8.00\,\text{cm}-2.00\,\text{cm}}{3.00\,\text{s}-0.00\,\text{s}}=2.00\,\text{cm/s}.[/latex]
3. The period is [latex]T=\frac{\lambda }{v}=\frac{8.00\,\text{cm}}{2.00\,\text{cm/s}}=4.00\,\text{s}[/latex] and the frequency is [latex]f=\frac{1}{T}=\frac{1}{4.00\,\text{s}}=0.25\,\text{Hz}.[/latex]

Significance

Note that the wavelength can be found using any two successive identical points that repeat, having the same height and slope. You should choose two points that are most convenient. The displacement can also be found using any convenient point.