11 Angular Momentum
11.4 Precession of a Gyroscope
Learning Objectives
By the end of this section, you will be able to:
- Describe the physical processes underlying the phenomenon of precession
- Calculate the precessional angular velocity of a gyroscope
Figure shows a gyroscope, defined as a spinning disk in which the axis of rotation is free to assume any orientation. When spinning, the orientation of the spin axis is unaffected by the orientation of the body that encloses it. The body or vehicle enclosing the gyroscope can be moved from place to place and the orientation of the spin axis will remain the same. This makes gyroscopes very useful in navigation, especially where magnetic compasses can’t be used, such as in manned and unmanned spacecraft, intercontinental ballistic missiles, unmanned aerial vehicles, and satellites like the Hubble Space Telescope.

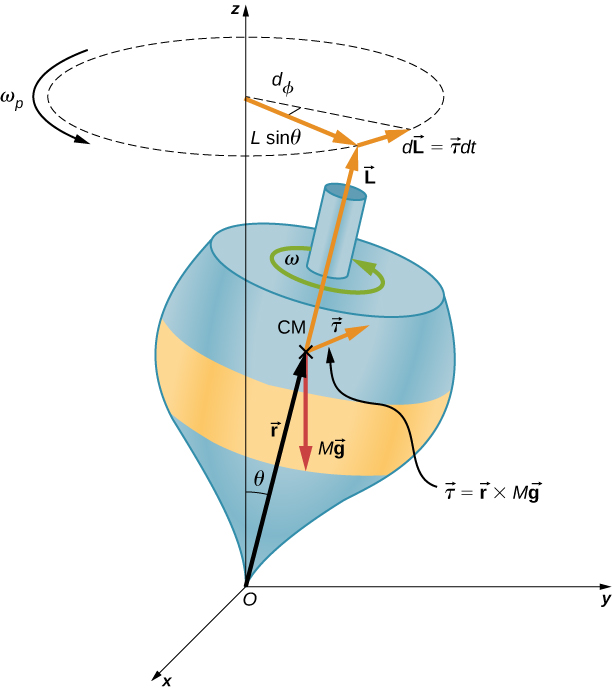
We illustrate the precession of a gyroscope with an example of a top in the next two figures. If the top is placed on a flat surface near the surface of Earth at an angle to the vertical and is not spinning, it will fall over, due to the force of gravity producing a torque acting on its center of mass. This is shown in Figure(a). However, if the top is spinning on its axis, rather than topple over due to this torque, it precesses about the vertical, shown in part (b) of the figure. This is due to the torque on the center of mass, which provides the change in angular momentum.
Figure shows the forces acting on a spinning top. The torque produced is perpendicular to the angular momentum vector. This changes the direction of the angular momentum vector [latex]\mathbf{\overset{\to }{L}}[/latex] according to [latex]d\mathbf{\overset{\to }{L}}=\mathbf{\overset{\to }{\tau }}dt,[/latex] but not its magnitude. The top precesses around a vertical axis, since the torque is always horizontal and perpendicular to [latex]\mathbf{\overset{\to }{L}}[/latex]. If the top is not spinning, it acquires angular momentum in the direction of the torque, and it rotates around a horizontal axis, falling over just as we would expect.
We can experience this phenomenon first hand by holding a spinning bicycle wheel and trying to rotate it about an axis perpendicular to the spin axis. As shown in Figure, the person applies forces perpendicular to the spin axis in an attempt to rotate the wheel, but instead, the wheel axis starts to change direction to her left due to the applied torque.
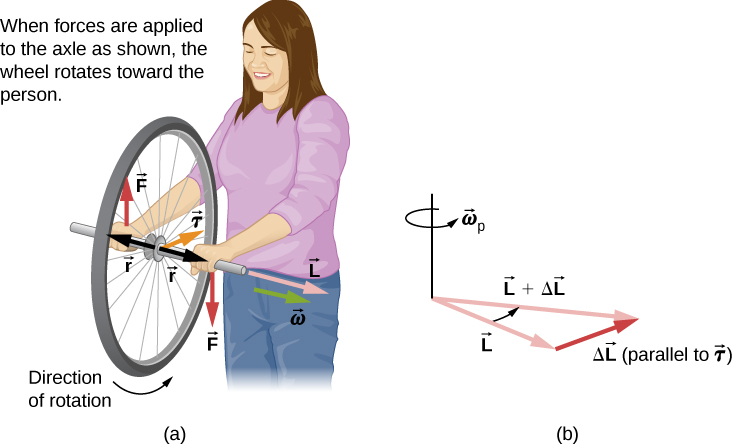
We all know how easy it is for a bicycle to tip over when sitting on it at rest. But when riding the bicycle at a good pace, it is harder to tip it over because we must change the angular momentum vector of the spinning wheels.
View the video on gyroscope precession for a complete demonstration of precession of the bicycle wheel.
Also, when a spinning disk is put in a box such as a Blu-Ray player, try to move it. It is easy to translate the box in a given direction but difficult to rotate it about an axis perpendicular to the axis of the spinning disk, since we are putting a torque on the box that will cause the angular momentum vector of the spinning disk to precess.
We can calculate the precession rate of the top in Figure. From Figure, we see that the magnitude of the torque is
Thus,
The angle the top precesses through in time dt is
The precession angular velocity is [latex]{\omega }_{P}=\frac{d\varphi }{dt}[/latex] and from this equation we see that
In this derivation, we assumed that [latex]{\omega }_{P}\ll \omega ,[/latex] that is, that the precession angular velocity is much less than the angular velocity of the gyroscope disk. The precession angular velocity adds a small component to the angular momentum along the z-axis. This is seen in a slight bob up and down as the gyroscope precesses, referred to as nutation.
Earth itself acts like a gigantic gyroscope. Its angular momentum is along its axis and currently points at Polaris, the North Star. But Earth is slowly precessing (once in about 26,000 years) due to the torque of the Sun and the Moon on its nonspherical shape.
Example
Period of Precession
A gyroscope spins with its tip on the ground and is spinning with negligible frictional resistance. The disk of the gyroscope has mass 0.3 kg and is spinning at 20 rev/s. Its center of mass is 5.0 cm from the pivot and the radius of the disk is 5.0 cm. What is the precessional period of the gyroscope?
Strategy
We use Figure to find the precessional angular velocity of the gyroscope. This allows us to find the period of precession.
Solution
The moment of inertia of the disk is
The angular velocity of the disk is
We can now substitute in Figure. The precessional angular velocity is
The precessional period of the gyroscope is
Significance
The precessional angular frequency of the gyroscope, 3.12 rad/s, or about 0.5 rev/s, is much less than the angular velocity 20 rev/s of the gyroscope disk. Therefore, we don’t expect a large component of the angular momentum to arise due to precession, and Figure is a good approximation of the precessional angular velocity.
Check Your Understanding
A top has a precession frequency of 5.0 rad/s on Earth. What is its precession frequency on the Moon?
The Moon’s gravity is 1/6 that of Earth’s. By examining (Figure), we see that the top’s precession frequency is linearly proportional to the acceleration of gravity. All other quantities, mass, moment of inertia, and spin rate are the same on the Moon. Thus, the precession frequency on the Moon is [latex]{\omega }_{P}\text{(Moon)}=\frac{1}{6}{\omega }_{P}\text{(Earth)}=\frac{1}{6}(5.0\,\text{rad}\text{/}\text{s})=0.83\,\text{rad}\text{/}\text{s}.[/latex]Show Answer
Summary
- When a gyroscope is set on a pivot near the surface of Earth, it precesses around a vertical axis, since the torque is always horizontal and perpendicular to [latex]\mathbf{\overset{\to }{L}}.[/latex] If the gyroscope is not spinning, it acquires angular momentum in the direction of the torque, and it rotates about a horizontal axis, falling over just as we would expect.
- The precessional angular velocity is given by [latex]{\omega }_{P}=\frac{rMg}{I\omega }[/latex], where r is the distance from the pivot to the center of mass of the gyroscope, I is the moment of inertia of the gyroscope’s spinning disk, M is its mass, and [latex]\omega[/latex] is the angular frequency of the gyroscope disk.
Key Equations
| Velocity of center of mass of rolling object | [latex]{v}_{\text{CM}}=R\omega[/latex] |
| Acceleration of center of mass of rolling object | [latex]{a}_{\text{CM}}=R\alpha[/latex] |
| Displacement of center of mass of rolling object | [latex]{d}_{\text{CM}}=R\theta[/latex] |
| Acceleration of an object rolling without slipping | [latex]{a}_{\text{CM}}=\frac{mg\,\text{sin}\,\theta }{m+({I}_{\text{CM}}\text{/}{r}^{2})}[/latex] |
| Angular momentum | [latex]\mathbf{\overset{\to }{l}}=\mathbf{\overset{\to }{r}}\times \mathbf{\overset{\to }{p}}[/latex] |
| Derivative of angular momentum equals torque | [latex]\frac{d\mathbf{\overset{\to }{l}}}{dt}=\sum \mathbf{\overset{\to }{\tau }}[/latex] |
| Angular momentum of a system of particles | [latex]\mathbf{\overset{\to }{L}}={\mathbf{\overset{\to }{l}}}_{1}+{\mathbf{\overset{\to }{l}}}_{2}+\cdots +{\mathbf{\overset{\to }{l}}}_{N}[/latex] |
| For a system of particles, derivative of angular
momentum equals torque |
[latex]\frac{d\mathbf{\overset{\to }{L}}}{dt}=\sum \mathbf{\overset{\to }{\tau }}[/latex] |
| Angular momentum of a rotating rigid body | [latex]L=I\omega[/latex] |
| Conservation of angular momentum | [latex]\frac{d\mathbf{\overset{\to }{L}}}{dt}=0[/latex] |
| Conservation of angular momentum | [latex]\mathbf{\overset{\to }{L}}={\mathbf{\overset{\to }{l}}}_{1}+{\mathbf{\overset{\to }{l}}}_{2}+\cdots +{\mathbf{\overset{\to }{l}}}_{N}=\text{constant}[/latex] |
| Precessional angular velocity | [latex]{\omega }_{P}=\frac{rMg}{I\omega }[/latex] |
Conceptual Questions
Gyroscopes used in guidance systems to indicate directions in space must have an angular momentum that does not change in direction. When placed in the vehicle, they are put in a compartment that is separated from the main fuselage, such that changes in the orientation of the fuselage does not affect the orientation of the gyroscope. If the space vehicle is subjected to large forces and accelerations how can the direction of the gyroscopes angular momentum be constant at all times?
Show Solution
A torque is needed in the direction perpendicular to the angular momentum vector in order to change its direction. These forces on the space vehicle are external to the container in which the gyroscope is mounted and do not impart torques to the gyroscope’s rotating disk.
Earth precesses about its vertical axis with a period of 26,000 years. Discuss whether Figure can be used to calculate the precessional angular velocity of Earth.
Problems
A gyroscope has a 0.5-kg disk that spins at 40 rev/s. The center of mass of the disk is 10 cm from a pivot which is also the radius of the disk. What is the precession angular velocity?
Show Solution
[latex]I=2.5\times {10}^{-3}\,\text{kg}\cdot {\text{m}}^{2}[/latex],
[latex]{\omega }_{P}=0.78\,\text{rad}\text{/}\text{s}[/latex]
The precession angular velocity of a gyroscope is 1.0 rad/s. If the mass of the rotating disk is 0.4 kg and its radius is 30 cm, as well as the distance from the center of mass to the pivot, what is the rotation rate in rev/s of the disk?
The axis of Earth makes a [latex]23.5^\circ[/latex] angle with a direction perpendicular to the plane of Earth’s orbit. As shown below, this axis precesses, making one complete rotation in 25,780 y.
(a) Calculate the change in angular momentum in half this time.
(b) What is the average torque producing this change in angular momentum?
(c) If this torque were created by a pair of forces acting at the most effective point on the equator, what would the magnitude of each force be?

a. [latex]{L}_{\text{Earth}}=7.06\times {10}^{33}\,\text{kg}\cdot {\text{m}}^{2}\text{/}\text{s}[/latex], [latex]\Delta L=5.63\times {10}^{33}\,\text{kg}\cdot {\text{m}}^{2}\text{/}\text{s}[/latex]; b. [latex]\tau =1.7\times {10}^{22}\,\text{N}\cdot \text{m}[/latex]; c. The two forces at the equator would have the same magnitude but different directions, one in the north direction and the other in the south direction on the opposite side of Earth. The angle between the forces and the lever arms to the center of Earth is [latex]90^\circ[/latex], so a given torque would have magnitude [latex]\tau =F{R}_{\text{E}}\,\text{sin}\,90^\circ=F{R}_{\text{E}}[/latex]. Both would provide a torque in the same direction: [latex]\tau =2F{R}_{\text{E}}\Rightarrow F=1.3\times {10}^{15}\,\text{N}[/latex]Show Answer
Additional Problems
A marble is rolling across the floor at a speed of 7.0 m/s when it starts up a plane inclined at [latex]30^\circ[/latex] to the horizontal. (a) How far along the plane does the marble travel before coming to a rest? (b) How much time elapses while the marble moves up the plane?
Repeat the preceding problem replacing the marble with a hollow sphere. Explain the new results.
Show Solution
[latex]{a}_{\text{CM}}=-\frac{3}{10}g[/latex],
[latex]{v}^{2}={v}_{0}^{2}+2{a}_{\text{CM}}x\Rightarrow {v}^{2}=(7.0\,\text{m}\text{/}{\text{s})}^{2}-2(\frac{3}{10}g)x,[/latex] [latex]{v}^{2}=0\Rightarrow x=8.34\,\text{m;}[/latex]
b. [latex]t=\frac{v-{v}_{0}}{{a}_{\text{CM}}},\enspace[/latex] [latex]v={v}_{0}+{a}_{\text{CM}}t\Rightarrow t=2.38\,\text{s}[/latex];
The hollow sphere has a larger moment of inertia, and therefore is harder to bring to a rest than the marble, or solid sphere. The distance travelled is larger and the time elapsed is longer.
The mass of a hoop of radius 1.0 m is 6.0 kg. It rolls across a horizontal surface with a speed of 10.0 m/s. (a) How much work is required to stop the hoop? (b) If the hoop starts up a surface at [latex]30^\circ[/latex] to the horizontal with a speed of 10.0 m/s, how far along the incline will it travel before stopping and rolling back down?
Repeat the preceding problem for a hollow sphere of the same radius and mass and initial speed. Explain the differences in the results.
Show Solution
a. [latex]W=-500.0\,\text{J}[/latex];
b. [latex]K+{U}_{\text{grav}}=\text{constant}[/latex],
[latex]500\,\text{J}\,+0=0+(6.0\,\text{kg})(9.8\,\text{m}\text{/}{\text{s}}^{2})h[/latex],
[latex]h=8.5\,\text{m,}d=17.0\,\text{m}[/latex];
The moment of inertia is less for the hollow sphere, therefore less work is required to stop it. Likewise it rolls up the incline a shorter distance than the hoop.
A particle has mass 0.5 kg and is traveling along the line [latex]x=5.0\,\text{m}[/latex] at 2.0 m/s in the positive y-direction. What is the particle’s angular momentum about the origin?
A 4.0-kg particle moves in a circle of radius 2.0 m. The angular momentum of the particle varies in time according to [latex]l=5.0{t}^{2}.[/latex] (a) What is the torque on the particle about the center of the circle at [latex]t=3.4\,\text{s}[/latex]? (b) What is the angular velocity of the particle at [latex]t=3.4\,\text{s}[/latex]?
Show Solution
a. [latex]\tau =34.0\,\text{N}\cdot \text{m}[/latex];
b. [latex]l=m{r}^{2}\omega \Rightarrow \omega =3.6\,\text{rad}\text{/}\text{s}[/latex]
A proton is accelerated in a cyclotron to [latex]5.0\times {10}^{6}\,\text{m}\text{/}\text{s}[/latex] in 0.01 s. The proton follows a circular path. If the radius of the cyclotron is 0.5 km, (a) What is the angular momentum of the proton about the center at its maximum speed? (b) What is the torque on the proton about the center as it accelerates to maximum speed?
(a) What is the angular momentum of the Moon in its orbit around Earth? (b) How does this angular momentum compare with the angular momentum of the Moon on its axis? Remember that the Moon keeps one side toward Earth at all times.
Show Solution
a. [latex]{d}_{\text{M}}=3.85\times {10}^{8}\,\text{m}[/latex] average distance to the Moon; orbital period [latex]27.32\text{d}=2.36\times {10}^{6}\text{s}[/latex]; speed of the Moon [latex]\frac{2\pi 3.85\times {10}^{8}\,\text{m}}{2.36\times {10}^{6}\text{s}}=1.0\times {10}^{3}\,\text{m}\text{/}\text{s}[/latex]; mass of the Moon [latex]7.35\times {10}^{22}\,\text{kg}[/latex],
[latex]L=2.90\times {10}^{34}\,\text{kg}{\text{m}}^{2}\text{/}\text{s}[/latex];
b. radius of the Moon [latex]1.74\times {10}^{6}\,\text{m}[/latex]; the orbital period is the same as (a): [latex]\omega =2.66\times {10}^{-6}\,\text{rad}\text{/}\text{s}[/latex],
[latex]L=2.37\times {10}^{29}\,\text{kg}\cdot {\text{m}}^{2}\text{/}\text{s}[/latex];
The orbital angular momentum is [latex]1.22\times {10}^{5}[/latex] times larger than the rotational angular momentum for the Moon.
A DVD is rotating at 500 rpm. What is the angular momentum of the DVD if has a radius of 6.0 cm and mass 20.0 g?
A potter’s disk spins from rest up to 10 rev/s in 15 s. The disk has a mass 3.0 kg and radius 30.0 cm. What is the angular momentum of the disk at [latex]t=5\,\text{s,}\,t=1\text{0 s}[/latex]?
Show Solution
[latex]I=0.135\,\text{kg}\cdot {\text{m}}^{2}[/latex],
[latex]\alpha =4.19\,\text{rad}\text{/}{\text{s}}^{2},[/latex] [latex]\omega ={\omega }_{0}+\alpha t[/latex],
[latex]\omega (5\,\text{s})=21.0\,\text{rad}\text{/}\text{s},[/latex] [latex]L=2.84\,\text{kg}\cdot {\text{m}}^{2}\text{/}\text{s}[/latex],
[latex]\omega (10\,\text{s})=41.9\,\text{rad}\text{/}\text{s},[/latex] [latex]L=5.66\,\text{kg}\cdot \text{m}\text{/}{\text{s}}^{2}[/latex]
Suppose you start an antique car by exerting a force of 300 N on its crank for 0.250 s. What is the angular momentum given to the engine if the handle of the crank is 0.300 m from the pivot and the force is exerted to create maximum torque the entire time?
A solid cylinder of mass 2.0 kg and radius 20 cm is rotating counterclockwise around a vertical axis through its center at 600 rev/min. A second solid cylinder of the same mass is rotating clockwise around the same vertical axis at 900 rev/min. If the cylinders couple so that they rotate about the same vertical axis, what is the angular velocity of the combination?
Show Solution
In the conservation of angular momentum equation, the rotation rate appears on both sides so we keep the (rev/min) notation as the angular velocity can be multiplied by a constant to get (rev/min):
[latex]\begin{array}{ccc}\hfill {L}_{\text{i}}& =\hfill & -0.04\,\text{kg}\cdot {\text{m}}^{2}(300.0\,\text{rev}\text{/}\text{min),}\hfill \\ \hfill {L}_{\text{f}}& =\hfill & 0.08\,\text{kg}\cdot {\text{m}}^{2}{f}_{\text{f}}\Rightarrow {f}_{\text{f}}=-150.0\,\text{rev}\text{/}\text{min clockwise}\hfill \end{array}[/latex]
A boy stands at the center of a platform that is rotating without friction at 1.0 rev/s. The boy holds weights as far from his body as possible. At this position the total moment of inertia of the boy, platform, and weights is [latex]5.0\,\text{kg}\cdot {\text{m}}^{2}.[/latex] The boy draws the weights in close to his body, thereby decreasing the total moment of inertia to [latex]1.5\,\text{kg}\cdot {\text{m}}^{2}.[/latex] (a) What is the final angular velocity of the platform? (b) By how much does the rotational kinetic energy increase?
Eight children, each of mass 40 kg, climb on a small merry-go-round. They position themselves evenly on the outer edge and join hands. The merry-go-round has a radius of 4.0 m and a moment of inertia [latex]1000.0\,\text{kg}\cdot {\text{m}}^{2}[/latex]. After the merry-go-round is given an angular velocity of 6.0 rev/min, the children walk inward and stop when they are 0.75 m from the axis of rotation. What is the new angular velocity of the merry-go-round? Assume there is negligible frictional torque on the structure.
Show Solution
[latex]{I}_{0}{\omega }_{0}={I}_{\text{f}}{\omega }_{\text{f}}[/latex],
[latex]{I}_{0}=6120.0\,\text{kg}\cdot {\text{m}}^{2}[/latex],
[latex]{I}_{\text{f}}=1180.0\,\text{kg}\cdot {\text{m}}^{2}[/latex],
[latex]{\omega }_{\text{f}}=31.1\,\text{rev}\text{/}\text{min}[/latex]
A thin meter stick of mass 150 g rotates around an axis perpendicular to the stick’s long axis at an angular velocity of 240 rev/min. What is the angular momentum of the stick if the rotation axis (a) passes through the center of the stick? (b) Passes through one end of the stick?
A satellite in the shape of a sphere of mass 20,000 kg and radius 5.0 m is spinning about an axis through its center of mass. It has a rotation rate of 8.0 rev/s. Two antennas deploy in the plane of rotation extending from the center of mass of the satellite. Each antenna can be approximated as a rod has mass 200.0 kg and length 7.0 m. What is the new rotation rate of the satellite?
Show Solution
[latex]{L}_{\text{i}}=1.00\times {10}^{7}\,\text{kg}\cdot {\text{m}}^{2}\text{/}\text{s}[/latex],
[latex]{I}_{\text{f}}=2.025\times {10}^{5}\,\text{kg}\cdot {\text{m}}^{2}[/latex],
[latex]{\omega }_{\text{f}}=7.86\,\text{rev}\text{/}\text{s}[/latex]
A top has moment of inertia [latex]3.2\times {10}^{-4}\,\text{kg}\cdot {\text{m}}^{2}[/latex] and radius 4.0 cm from the center of mass to the pivot point. If it spins at 20.0 rev/s and is precessing, how many revolutions does it precess in 10.0 s?
Challenge Problems
The truck shown below is initially at rest with solid cylindrical roll of paper sitting on its bed. If the truck moves forward with a uniform acceleration a, what distance s does it move before the paper rolls off its back end? (Hint: If the roll accelerates forward with [latex]{a}^{\prime }[/latex], then is accelerates backward relative to the truck with an acceleration [latex]a-{a}^{\prime }[/latex]. Also, [latex]R\alpha =a-{a}^{\prime }[/latex].)

Assume the roll accelerates forward with respect to the ground with an acceleration [latex]{a}^{\prime }[/latex]. Then it accelerates backwards relative to the truck with an acceleration [latex](a-{a}^{\prime })[/latex].

Show Answer
Also, [latex]R\alpha =a-{a}^{\prime }\,I=\frac{1}{2}m{R}^{2}\enspace\sum {F}_{x}={f}_{s}=m{a}^{\prime }[/latex], [latex]\sum \tau ={f}_{s}R=I\alpha =I\frac{a-{a}^{\prime }}{R}\enspace{f}_{s}=\frac{I}{{R}^{2}}(a-{a}^{\prime })=\frac{1}{2}m(a-{a}^{\prime })[/latex], Solving for [latex]{a}^{\prime }[/latex]: [latex]\enspace{f}_{s}=\frac{1}{2}m(a-{a}^{\prime })[/latex]; [latex]{a}^{\prime }=\frac{a}{3}[/latex], [latex]x-{x}_{0}={v}_{0}t+\frac{1}{2}a{t}^{2};d=\frac{1}{3}a{t}^{2};t=\sqrt{\frac{3d}{a}};[/latex] therefore, [latex]s=1.5d[/latex]
A bowling ball of radius 8.5 cm is tossed onto a bowling lane with speed 9.0 m/s. The direction of the toss is to the left, as viewed by the observer, so the bowling ball starts to rotate counterclockwise when in contact with the floor. The coefficient of kinetic friction on the lane is 0.3. (a) What is the time required for the ball to come to the point where it is not slipping? What is the distance d to the point where the ball is rolling without slipping?
A small ball of mass 0.50 kg is attached by a massless string to a vertical rod that is spinning as shown below. When the rod has an angular velocity of 6.0 rad/s, the string makes an angle of [latex]30^\circ[/latex] with respect to the vertical. (a) If the angular velocity is increased to 10.0 rad/s, what is the new angle of the string? (b) Calculate the initial and final angular momenta of the ball. (c) Can the rod spin fast enough so that the ball is horizontal?

a. The tension in the string provides the centripetal force such that [latex]T\,\text{sin}\,\theta =m{r}_{\perp }{\omega }^{2}[/latex]. The component of the tension that is vertical opposes the gravitational force such that [latex]T\,\text{cos}\,\theta =mg[/latex]. This gives [latex]T=5.7\,\text{N}[/latex]. We solve for [latex]{r}_{\perp }=0.16\,\text{m}[/latex]. This gives the length of the string as [latex]r=0.32\,\text{m}[/latex]. At [latex]\omega =10.0\,\text{rad}\text{/}\text{s}[/latex], there is a new angle, tension, and perpendicular radius to the rod. Dividing the two equations involving the tension to eliminate it, we have [latex]\frac{\text{sin}\,\theta }{\text{cos}\,\theta }=\frac{(0.32\,\text{m}\,\text{sin}\,\theta ){\omega }^{2}}{g}\Rightarrow \frac{1}{\text{cos}\,\theta }=\frac{0.32\,\text{m}{\omega }^{2}}{g}[/latex]; [latex]\text{cos}\,\theta =0.31\Rightarrow \theta =72.2^\circ[/latex]; b. [latex]{l}_{\text{initial}}=0.08\,\text{kg}\cdot {\text{m}}^{2}\text{/}\text{s}[/latex], [latex]{l}_{\text{final}}=0.46\,\text{kg}\cdot {\text{m}}^{2}\text{/}\text{s}[/latex]; c. No, the cosine of the angle is inversely proportional to the square of the angular velocity, therefore in order for [latex]\theta \to 90^\circ,\enspace\omega \to \infty[/latex]. The rod would have to spin infinitely fast.Show Answer
A bug flying horizontally at 1.0 m/s collides and sticks to the end of a uniform stick hanging vertically. After the impact, the stick swings out to a maximum angle of [latex]5.0^\circ[/latex] from the vertical before rotating back. If the mass of the stick is 10 times that of the bug, calculate the length of the stick.
Glossary
- precession
- circular motion of the pole of the axis of a spinning object around another axis due to a torque
