Wave-Particle Duality

Samuel J. Ling; Jeff Sanny; William Moebs

Photons and Matter Waves

Wave-Particle Duality

Samuel J. Ling; Jeff Sanny; and William Moebs

Learning Objectives

By the end of this section, you will be able to:

Identify phenomena in which electromagnetic waves behave like a beam of photons and particles behave like waves
Describe the physics principles behind electron microscopy
Summarize the evolution of scientific thought that led to the development of quantum mechanics

The energy of radiation detected by a radio-signal receiving antenna comes as the energy of an electromagnetic wave. The same energy of radiation detected by a photocurrent in the photoelectric effect comes as the energy of individual photon particles. Therefore, the question arises about the nature of electromagnetic radiation: Is a photon a wave or is it a particle? Similar questions may be asked about other known forms of energy. For example, an electron that forms part of an electric current in a circuit behaves like a particle moving in unison with other electrons inside the conductor. The same electron behaves as a wave when it passes through a solid crystalline structure and forms a diffraction image. Is an electron a wave or is it a particle? The same question can be extended to all particles of matter—elementary particles, as well as compound molecules—asking about their true physical nature. At our present state of knowledge, such questions about the true nature of things do not have conclusive answers. All we can say is that wave-particle duality exists in nature: Under some experimental conditions, a particle appears to act as a particle, and under different experimental conditions, a particle appears to act a wave. Conversely, under some physical circumstances electromagnetic radiation acts as a wave, and under other physical circumstances, radiation acts as a beam of photons.

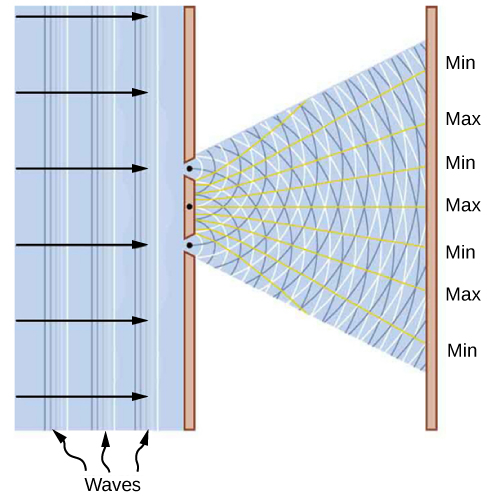
This dualistic interpretation is not a new physics concept brought about by specific discoveries in the twentieth century. It was already present in a debate between Isaac Newton and Christiaan Huygens about the nature of light, beginning in the year 1670. According to Newton, a beam of light is a collection of corpuscles of light. According to Huygens, light is a wave. The corpuscular hypothesis failed in 1803, when Thomas Young announced his double-slit interference experiment with light (see (Figure)), which firmly established light as a wave. In James Clerk Maxwell’s theory of electromagnetism (completed by the year 1873), light is an electromagnetic wave. Maxwell’s classical view of radiation as an electromagnetic wave is still valid today; however, it is unable to explain blackbody radiation and the photoelectric effect, where light acts as a beam of photons.

Young’s double-slit experiment explains the interference of light by making an analogy with the interference of water waves. Two waves are generated at the positions of two slits in an opaque screen. The waves have the same wavelengths. They travel from their origins at the slits to the viewing screen placed to the right of the slits. The waves meet on the viewing screen. At the positions marked “Max” on the screen, the meeting waves are in-phase and the combined wave amplitude is enhanced. At positions marked “Min,” the combined wave amplitude is zero. For light, this mechanism creates a bright-and-dark fringe pattern on the viewing screen.

Picture is the schematics of the Young’s double-slit experiment. Parallel waves are incident to the opaque screen with the two small slits. Two new waves are generated at the positions of these slits. They travel from the origins at the slits and meet at the viewing screen placed to the right of the slits creating a number in-phase, marked “Max”, and zero amplitude, marked “Min,” combinations.

A similar dichotomy existed in the interpretation of electricity. From Benjamin Franklin’s observations of electricity in 1751 until J.J. Thomson’s discovery of the electron in 1897, electric current was seen as a flow in a continuous electric medium. Within this theory of electric fluid, the present theory of electric circuits was developed, and electromagnetism and electromagnetic induction were discovered. Thomson’s experiment showed that the unit of negative electric charge (an electron) can travel in a vacuum without any medium to carry the charge around, as in electric circuits. This discovery changed the way in which electricity is understood today and gave the electron its particle status. In Bohr’s early quantum theory of the hydrogen atom, both the electron and the proton are particles of matter. Likewise, in the Compton scattering of X-rays on electrons, the electron is a particle. On the other hand, in electron-scattering experiments on crystalline structures, the electron behaves as a wave.

A skeptic may raise a question that perhaps an electron might always be nothing more than a particle, and that the diffraction images obtained in electron-scattering experiments might be explained within some macroscopic model of a crystal and a macroscopic model of electrons coming at it like a rain of ping-pong balls. As a matter of fact, to investigate this question, we do not need a complex model of a crystal but just a couple of simple slits in a screen that is opaque to electrons. In other words, to gather convincing evidence about the nature of an electron, we need to repeat the Young double-slit experiment with electrons. If the electron is a wave, we should observe the formation of interference patterns typical for waves, such as those described in (Figure), even when electrons come through the slits one by one. However, if the electron is a not a wave but a particle, the interference fringes will not be formed.

The very first double-slit experiment with a beam of electrons, performed by Claus Jönsson in Germany in 1961, demonstrated that a beam of electrons indeed forms an interference pattern, which means that electrons collectively behave as a wave. The first double-slit experiments with single electrons passing through the slits one-by-one were performed by Giulio Pozzi in 1974 in Italy and by Akira Tonomura in 1989 in Japan. They show that interference fringes are formed gradually, even when electrons pass through the slits individually. This demonstrates conclusively that electron-diffraction images are formed because of the wave nature of electrons. The results seen in double-slit experiments with electrons are illustrated by the images of the interference pattern in (Figure).

Computer-simulated interference fringes seen in the Young double-slit experiment with electrons. One pattern is gradually formed on the screen, regardless of whether the electrons come through the slits as a beam or individually one-by-one.

Picture shows five images of computer-simulated interference fringes seen in the Young double-slit experiment with electrons. All images show the equidistantly spaced fringes. While the fringe intensity increases with the number of electrons passing through the slits, the pattern remains the same.

Double-Slit Experiment with Electrons In one experimental setup for studying interference patterns of electron waves, two slits are created in a gold-coated silicon membrane. Each slit is 62-nm wide and $4\text{-μ}\text{m}$ long, and the separation between the slits is 272 nm. The electron beam is created in an electron gun by heating a tungsten element and by accelerating the electrons across a 600-V potential. The beam is subsequently collimated using electromagnetic lenses, and the collimated beam of electrons is sent through the slits. Find the angular position of the first-order bright fringe on the viewing screen.

Strategy Recall that the angular position $\theta$ of the nth order bright fringe that is formed in Young’s two-slit interference pattern (discussed in a previous chapter) is related to the separation, d, between the slits and to the wavelength, $\lambda ,$ of the incident light by the equation $d\text{sin}\theta =n\lambda ,$ where $n=0,±1,±2,....$ The separation is given and is equal to $d=272\phantom{\rule{0.2em}{0ex}}\text{nm}.$ For the first-order fringe, we take $n=1.$ The only thing we now need is the wavelength of the incident electron wave.

Since the electron has been accelerated from rest across a potential difference of $\text{Δ}V=600\text{V},$ its kinetic energy is $K=e\text{Δ}V=600\phantom{\rule{0.2em}{0ex}}\text{eV}.$ The rest-mass energy of the electron is ${E}_{0}=511\phantom{\rule{0.2em}{0ex}}\text{keV}.$

We compute its de Broglie wavelength as that of a nonrelativistic electron because its kinetic energy $K$ is much smaller than its rest energy ${E}_{0},$ $K\ll {E}_{0}.$

Solution The electron’s wavelength is

$\lambda =\frac{h}{p}=\frac{h}{\sqrt{2{m}_{e}K}}=\frac{h}{\sqrt{2{E}_{0}\phantom{\rule{0.1em}{0ex}}\text{/}\phantom{\rule{0.1em}{0ex}}{c}^{2}K}}=\frac{hc}{\sqrt{2{E}_{0}K}}=\frac{1.241\phantom{\rule{0.2em}{0ex}}×\phantom{\rule{0.2em}{0ex}}{10}^{-6}\text{eV}·\text{m}}{\sqrt{2\left(511\phantom{\rule{0.2em}{0ex}}\text{keV}\right)\left(600\phantom{\rule{0.2em}{0ex}}\text{eV}\right)}}=0.050\phantom{\rule{0.2em}{0ex}}\text{nm}.$

This $\lambda$ is used to obtain the position of the first bright fringe:

$\text{sin}\theta =\frac{1·\lambda }{d}=\frac{0.050\phantom{\rule{0.2em}{0ex}}\text{nm}}{272\phantom{\rule{0.2em}{0ex}}\text{nm}}=0.000184⇒\theta =0.010\text{°}.$

Significance Notice that this is also the angular resolution between two consecutive bright fringes up to about $n=1000.$ For example, between the zero-order fringe and the first-order fringe, between the first-order fringe and the second-order fringe, and so on.

Check Your Understanding For the situation described in (Figure), find the angular position of the fifth-order bright fringe on the viewing screen.

$0.052\text{°}$

The wave-particle dual nature of matter particles and of radiation is a declaration of our inability to describe physical reality within one unified classical theory because separately neither a classical particle approach nor a classical wave approach can fully explain the observed phenomena. This limitation of the classical approach was realized by the year 1928, and a foundation for a new statistical theory, called quantum mechanics, was put in place by Bohr, Edwin Schrödinger, Werner Heisenberg, and Paul Dirac. Quantum mechanics takes de Broglie’s idea of matter waves to be the fundamental property of all particles and gives it a statistical interpretation. According to this interpretation, a wave that is associated with a particle carries information about the probable positions of the particle and about its other properties. A single particle is seen as a moving wave packet such as the one shown in (Figure). We can intuitively sense from this example that if a particle is a wave packet, we will not be able to measure its exact position in the same sense as we cannot pinpoint a location of a wave packet in a vibrating guitar string. The uncertainty, $\text{Δ}x,$ in measuring the particle’s position is connected to the uncertainty, $\text{Δ}p,$ in the simultaneous measuring of its linear momentum by Heisenberg’s uncertainty principle:

$\text{Δ}x\text{Δ}p\ge \frac{1}{2}\hslash .$

Heisenberg’s principle expresses the law of nature that, at the quantum level, our perception is limited. For example, if we know the exact position of a body (which means that $\text{Δ}x=0$ in (Figure)) at the same time we cannot know its momentum, because then the uncertainty in its momentum becomes infinite (because $\text{Δ}p\ge 0.5\hslash \phantom{\rule{0.1em}{0ex}}\text{/}\phantom{\rule{0.1em}{0ex}}\text{Δ}x$ in (Figure)). The Heisenberg uncertainty principle sets the limit on the precision of simultaneous measurements of position and momentum of a particle; it shows that the best precision we can obtain is when we have an equals sign ( $=$ ) in (Figure), and we cannot do better than that, even with the best instruments of the future. Heisenberg’s principle is a consequence of the wave nature of particles.

In this graphic, a particle is shown as a wave packet and its position does not have an exact value.

Graphic shows a wave-packet that consist of sinusoidal oscillations with the different altitude.

We routinely use many electronic devices that exploit wave-particle duality without even realizing the sophistication of the physics underlying their operation. One example of a technology based on the particle properties of photons and electrons is a charge-coupled device, which is used for light detection in any instrumentation where high-quality digital data are required, such as in digital cameras or in medical sensors. An example in which the wave properties of electrons is exploited is an electron microscope.

In 1931, physicist Ernst Ruska—building on the idea that magnetic fields can direct an electron beam just as lenses can direct a beam of light in an optical microscope—developed the first prototype of the electron microscope. This development originated the field of electron microscopy. In the transmission electron microscope (TEM), shown in (Figure), electrons are produced by a hot tungsten element and accelerated by a potential difference in an electron gun, which gives them up to 400 keV in kinetic energy. After leaving the electron gun, the electron beam is focused by electromagnetic lenses (a system of condensing lenses) and transmitted through a specimen sample to be viewed. The image of the sample is reconstructed from the transmitted electron beam. The magnified image may be viewed either directly on a fluorescent screen or indirectly by sending it, for example, to a digital camera or a computer monitor. The entire setup consisting of the electron gun, the lenses, the specimen, and the fluorescent screen are enclosed in a vacuum chamber to prevent the energy loss from the beam. Resolution of the TEM is limited only by spherical aberration (discussed in a previous chapter). Modern high-resolution models of a TEM can have resolving power greater than 0.5 Å and magnifications higher than 50 million times. For comparison, the best resolving power obtained with light microscopy is currently about 97 nm. A limitation of the TEM is that the samples must be about 100-nm thick and biological samples require a special preparation involving chemical “fixing” to stabilize them for ultrathin slicing.

TEM: An electron beam produced by an electron gun is collimated by condenser lenses and passes through a specimen. The transmitted electrons are projected on a screen and the image is sent to a camera. (credit: modification of work by Dr. Graham Beards)

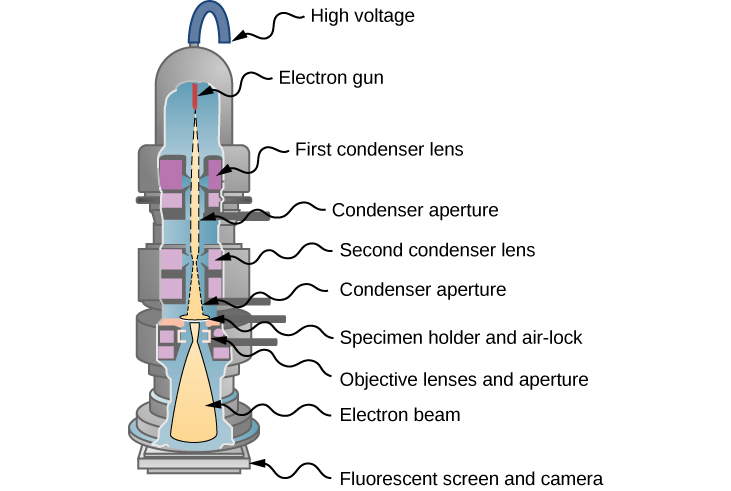
Picture shows the schematics of a transmission electron microscope. An electron gun generates electron beam that passes through two sets of condenser lens and condenser apertures prior to hitting the specimen. The transmitted electrons are projected on a fluorescent screen and the image is sent to a camera.

Such limitations do not appear in the scanning electron microscope (SEM), which was invented by Manfred von Ardenne in 1937. In an SEM, a typical energy of the electron beam is up to 40 keV and the beam is not transmitted through a sample but is scattered off its surface. Surface topography of the sample is reconstructed by analyzing back-scattered electrons, transmitted electrons, and the emitted radiation produced by electrons interacting with atoms in the sample. The resolving power of an SEM is better than 1 nm, and the magnification can be more than 250 times better than that obtained with a light microscope. The samples scanned by an SEM can be as large as several centimeters but they must be specially prepared, depending on electrical properties of the sample.

High magnifications of the TEM and SEM allow us to see individual molecules. High resolving powers of the TEM and SEM allow us to see fine details, such as those shown in the SEM micrograph of pollen at the beginning of this chapter ((Figure)).

Resolving Power of an Electron Microscope If a 1.0-pm electron beam of a TEM passes through a $2.0\text{-}\mu \text{m}$ circular opening, what is the angle between the two just-resolvable point sources for this microscope?

Solution We can directly use a formula for the resolving power, $\text{Δ}\theta ,$ of a microscope (discussed in a previous chapter) when the wavelength of the incident radiation is $\lambda =1.0\phantom{\rule{0.2em}{0ex}}\text{pm}$ and the diameter of the aperture is $D=2.0\mu \text{m}:$

$\text{Δ}\theta =1.22\frac{\lambda }{D}=1.22\frac{1.0\phantom{\rule{0.2em}{0ex}}\text{pm}}{2.0\mu \text{m}}=6.10\phantom{\rule{0.2em}{0ex}}×\phantom{\rule{0.2em}{0ex}}{10}^{-7}\text{rad}=3.50\phantom{\rule{0.2em}{0ex}}×\phantom{\rule{0.2em}{0ex}}{10}^{-5}\text{degree.}$

Significance Note that if we used a conventional microscope with a 400-nm light, the resolving power would be only $14\text{°},$ which means that all of the fine details in the image would be blurred.

Check Your Understanding Suppose that the diameter of the aperture in (Figure) is halved. How does it affect the resolving power?

doubles it

Summary

Wave-particle duality exists in nature: Under some experimental conditions, a particle acts as a particle; under other experimental conditions, a particle acts as a wave. Conversely, under some physical circumstances, electromagnetic radiation acts as a wave, and under other physical circumstances, radiation acts as a beam of photons.
Modern-era double-slit experiments with electrons demonstrated conclusively that electron-diffraction images are formed because of the wave nature of electrons.
The wave-particle dual nature of particles and of radiation has no classical explanation.
Quantum theory takes the wave property to be the fundamental property of all particles. A particle is seen as a moving wave packet. The wave nature of particles imposes a limitation on the simultaneous measurement of the particle’s position and momentum. Heisenberg’s uncertainty principle sets the limits on precision in such simultaneous measurements.
Wave-particle duality is exploited in many devices, such as charge-couple devices (used in digital cameras) or in the electron microscopy of the scanning electron microscope (SEM) and the transmission electron microscope (TEM).

Key Equations

Wien’s displacement law	${\lambda }_{\mathrm{max}}T=2.898\phantom{\rule{0.2em}{0ex}}×\phantom{\rule{0.2em}{0ex}}{10}^{-3}\text{m}\cdot \text{K}$
Stefan’s law	$P\left(T\right)=\sigma A{T}^{4}$
Planck’s constant	$h=6.626\phantom{\rule{0.2em}{0ex}}×\phantom{\rule{0.2em}{0ex}}{10}^{-34}\text{J}\cdot \text{s}=4.136\phantom{\rule{0.2em}{0ex}}×\phantom{\rule{0.2em}{0ex}}{10}^{-15}\text{eV}\cdot \text{s}$
Energy quantum of radiation	$\Delta E=hf$
Planck’s blackbody radiation law	$I\left(\lambda ,T\right)=\frac{2\pi h{c}^{2}}{{\lambda }^{5}}\phantom{\rule{0.2em}{0ex}}\frac{1}{{e}^{hc\phantom{\rule{0.1em}{0ex}}\text{/}\phantom{\rule{0.1em}{0ex}}\lambda {k}_{B}T}-1}$
Maximum kinetic energy of a photoelectron	${K}_{\mathrm{max}}=e\Delta {V}_{s}$
Energy of a photon	${E}_{f}=hf$
Energy balance for photoelectron	${K}_{\mathrm{max}}=hf-\varphi$
Cut-off frequency	${f}_{c}=\frac{\varphi }{h}$
Relativistic invariant energy equation	${E}^{2}={p}^{2}{c}^{2}+{m}_{0}^{2}{c}^{4}$
Energy-momentum relation for photon	${p}_{f}=\frac{{E}_{f}}{c}$
Energy of a photon	${E}_{f}=hf=\frac{hc}{\lambda }$
Magnitude of photon’s momentum	${p}_{f}=\frac{h}{\lambda }$
Photon’s linear momentum vector	${\stackrel{\to }{p}}_{f}=\hslash \stackrel{\to }{k}$
The Compton wavelength of an electron	${\lambda }_{c}=\frac{h}{{m}_{0}c}=0.00243\phantom{\rule{0.2em}{0ex}}\text{nm}$
The Compton shift	$\Delta \lambda ={\lambda }_{c}\left(1-\mathrm{cos}\theta \right)$
The Balmer formula	$\frac{1}{\lambda }={R}_{\text{H}}\left(\frac{1}{{2}^{2}}-\frac{1}{{n}^{2}}\right)$
The Rydberg formula	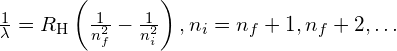$\frac{1}{\lambda }={R}_{\text{H}}\left(\frac{1}{{n}_{f}^{2}}-\frac{1}{{n}_{i}^{2}}\right),{n}_{i}={n}_{f}+1,{n}_{f}+2,\dots$
Bohr’s first quantization condition	${L}_{n}=n\hslash ,n=1,2,\dots$
Bohr’s second quantization condition	$hf=\|{E}_{n}-{E}_{m}\|$
Bohr’s radius of hydrogen	${a}_{0}=4\pi {\epsilon }_{0}\frac{{\hslash }^{2}}{{m}_{e}{e}^{2}}=0.529\text{Å}$
Bohr’s radius of the nth orbit	${r}_{n}={a}_{0}{n}^{2}$
Ground-state energy value, ionization limit	${E}_{0}=\frac{1}{8{\epsilon }_{0}^{2}}\phantom{\rule{0.2em}{0ex}}\frac{{m}_{e}{e}^{4}}{{h}^{2}}=13.6\phantom{\rule{0.2em}{0ex}}\text{eV}$
Electron’s energy in the nth orbit	${E}_{n}=-{E}_{0}\frac{1}{{n}^{2}}$
Ground state energy of hydrogen	${E}_{1}=-{E}_{0}=-13.6\phantom{\rule{0.2em}{0ex}}\text{eV}$
The nth orbit of hydrogen-like ion	${r}_{n}=\frac{{a}_{0}}{Z}{n}^{2}$
The nth energy of hydrogen-like ion	${E}_{n}=-{Z}^{2}{E}_{0}\frac{1}{{n}^{2}}$
Energy of a matter wave	$E=hf$
The de Broglie wavelength	$\lambda =\frac{h}{p}$
The frequency-wavelength relation for matter waves	$\lambda f=\frac{c}{\beta }$
Heisenberg’s uncertainty principle	$\Delta x\phantom{\rule{0.2em}{0ex}}\Delta p\ge \frac{1}{2}\hslash$

Conceptual Questions

Give an example of an experiment in which light behaves as waves. Give an example of an experiment in which light behaves as a stream of photons.

Discuss: How does the interference of water waves differ from the interference of electrons? How are they analogous?

Answers may vary

Give at least one argument in support of the matter-wave hypothesis.

Give at least one argument in support of the particle-nature of radiation.

Answers may vary

Explain the importance of the Young double-slit experiment.

Does the Heisenberg uncertainty principle allow a particle to be at rest in a designated region in space?

yes

Can the de Broglie wavelength of a particle be known exactly?

Do the photons of red light produce better resolution in a microscope than blue light photons? Explain.

yes

Discuss the main difference between an SEM and a TEM.

Problems

An AM radio transmitter radiates 500 kW at a frequency of 760 kHz. How many photons per second does the emitter emit?

$9.929\phantom{\rule{0.2em}{0ex}}×\phantom{\rule{0.2em}{0ex}}{10}^{32}$

Find the Lorentz factor $\gamma$ and de Broglie’s wavelength for a 50-GeV electron in a particle accelerator.

Find the Lorentz factor $\gamma$ and de Broglie’s wavelength for a 1.0-TeV proton in a particle accelerator.

$\gamma =1060;$ 0.00124 fm

What is the kinetic energy of a 0.01-nm electron in a TEM?

If electron is to be diffracted significantly by a crystal, its wavelength must be about equal to the spacing, d, of crystalline planes. Assuming $d=0.250\phantom{\rule{0.2em}{0ex}}\text{nm},$ estimate the potential difference through which an electron must be accelerated from rest if it is to be diffracted by these planes.

24.11 V

X-rays form ionizing radiation that is dangerous to living tissue and undetectable to the human eye. Suppose that a student researcher working in an X-ray diffraction laboratory is accidentally exposed to a fatal dose of radiation. Calculate the temperature increase of the researcher under the following conditions: the energy of X-ray photons is 200 keV and the researcher absorbs $4\phantom{\rule{0.2em}{0ex}}×\phantom{\rule{0.2em}{0ex}}{10}^{13}$ photons per each kilogram of body weight during the exposure. Assume that the specific heat of the student’s body is $0.83\text{kcal}\phantom{\rule{0.1em}{0ex}}\text{/}\phantom{\rule{0.1em}{0ex}}\text{kg}·\text{K}.$

Solar wind (radiation) that is incident on the top of Earth’s atmosphere has an average intensity of $1.3\text{kW}\phantom{\rule{0.1em}{0ex}}\text{/}\phantom{\rule{0.1em}{0ex}}{\text{m}}^{2}.$ Suppose that you are building a solar sail that is to propel a small toy spaceship with a mass of 0.1 kg in the space between the International Space Station and the moon. The sail is made from a very light material, which perfectly reflects the incident radiation. To assess whether such a project is feasible, answer the following questions, assuming that radiation photons are incident only in normal direction to the sail reflecting surface. (a) What is the radiation pressure (force per ${\text{m}}^{2}$ ) of the radiation falling on the mirror-like sail? (b) Given the radiation pressure computed in (a), what will be the acceleration of the spaceship when the sail has of an area of $10.0{\text{m}}^{2}$ ? (c) Given the acceleration estimate in (b), how fast will the spaceship be moving after 24 hours when it starts from rest?

a. $P=2I\phantom{\rule{0.1em}{0ex}}\text{/}\phantom{\rule{0.1em}{0ex}}c=8.67\phantom{\rule{0.2em}{0ex}}×\phantom{\rule{0.2em}{0ex}}{10}^{-6}\text{N}\phantom{\rule{0.1em}{0ex}}\text{/}\phantom{\rule{0.1em}{0ex}}{\text{m}}^{2};$ b. $a=PA\phantom{\rule{0.1em}{0ex}}\text{/}\phantom{\rule{0.1em}{0ex}}m=8.67\phantom{\rule{0.2em}{0ex}}×\phantom{\rule{0.2em}{0ex}}{10}^{-4}\text{m}\phantom{\rule{0.1em}{0ex}}\text{/}\phantom{\rule{0.1em}{0ex}}{\text{s}}^{2};$ c. 74.91 m/s

Treat the human body as a blackbody and determine the percentage increase in the total power of its radiation when its temperature increases from 98.6 $\text{°}$ F to 103 $\text{°}$ F.

Show that Wien’s displacement law results from Planck’s radiation law. (Hint: substitute $x=hc\phantom{\rule{0.1em}{0ex}}\text{/}\phantom{\rule{0.1em}{0ex}}\lambda kT$ and write Planck’s law in the form $I\left(x,T\right)=A{x}^{5}\phantom{\rule{0.1em}{0ex}}\text{/}\phantom{\rule{0.1em}{0ex}}\left({e}^{x}-1\right),$ where $A=2\pi {\left(kT\right)}^{5}\phantom{\rule{0.1em}{0ex}}\text{/}\phantom{\rule{0.1em}{0ex}}\left({h}^{4}{c}^{3}\right).$ Now, for fixed T, find the position of the maximum in I(x,T) by solving for x in the equation $dI\left(x,T\right)\phantom{\rule{0.1em}{0ex}}\text{/}\phantom{\rule{0.1em}{0ex}}dx=0.$ )

$x=4.965$

Show that Stefan’s law results from Planck’s radiation law. Hint: To compute the total power of blackbody radiation emitted across the entire spectrum of wavelengths at a given temperature, integrate Planck’s law over the entire spectrum $P\left(T\right)={\int }_{0}^{\infty }I\left(\lambda ,T\right)d\lambda .$ Use the substitution $x=hc\phantom{\rule{0.1em}{0ex}}\text{/}\phantom{\rule{0.1em}{0ex}}\lambda kT$ and the tabulated value of the integral ${\int }_{0}^{\infty }dx{x}^{3}\phantom{\rule{0.1em}{0ex}}\text{/}\phantom{\rule{0.1em}{0ex}}\left({e}^{x}-1\right)={\pi }^{4}\phantom{\rule{0.1em}{0ex}}\text{/}\phantom{\rule{0.1em}{0ex}}15.$

Additional Problems

Determine the power intensity of radiation per unit wavelength emitted at a wavelength of 500.0 nm by a blackbody at a temperature of 10,000 K.

$7.124\phantom{\rule{0.2em}{0ex}}×\phantom{\rule{0.2em}{0ex}}{10}^{16}{\text{W/m}}^{3}$

The HCl molecule oscillates at a frequency of 87.0 THz. What is the difference (in eV) between its adjacent energy levels?

A quantum mechanical oscillator vibrates at a frequency of 250.0 THz. What is the minimum energy of radiation it can emit?

1.034 eV

In about 5 billion years, the sun will evolve to a red giant. Assume that its surface temperature will decrease to about half its present value of 6000 K, while its present radius of $7.0\phantom{\rule{0.2em}{0ex}}×\phantom{\rule{0.2em}{0ex}}{10}^{8}\text{m}$ will increase to $1.5\phantom{\rule{0.2em}{0ex}}×\phantom{\rule{0.2em}{0ex}}{10}^{11}\text{m}$ (which is the current Earth-sun distance). Calculate the ratio of the total power emitted by the sun in its red giant stage to its present power.

A sodium lamp emits 2.0 W of radiant energy, most of which has a wavelength of about 589 nm. Estimate the number of photons emitted per second by the lamp.

$5.93\phantom{\rule{0.2em}{0ex}}×\phantom{\rule{0.2em}{0ex}}{10}^{18}$

Photoelectrons are ejected from a photoelectrode and are detected at a distance of 2.50 cm away from the photoelectrode. The work function of the photoelectrode is 2.71 eV and the incident radiation has a wavelength of 420 nm. How long does it take a photoelectron to travel to the detector?

If the work function of a metal is 3.2 eV, what is the maximum wavelength that a photon can have to eject a photoelectron from this metal surface?

387.8 nm

The work function of a photoelectric surface is 2.00 eV. What is the maximum speed of the photoelectrons emitted from this surface when a 450-nm light falls on it?

A 400-nm laser beam is projected onto a calcium electrode. The power of the laser beam is 2.00 mW and the work function of calcium is 2.31 eV. (a) How many photoelectrons per second are ejected? (b) What net power is carried away by photoelectrons?

a. $4.02\phantom{\rule{0.2em}{0ex}}×\phantom{\rule{0.2em}{0ex}}{10}^{15};$ b. 0.533 mW

(a) Calculate the number of photoelectrons per second that are ejected from a 1.00-mm² area of sodium metal by a 500-nm radiation with intensity $1.30{\text{kW/m}}^{2}$ (the intensity of sunlight above Earth’s atmosphere). (b) Given the work function of the metal as 2.28 eV, what power is carried away by these photoelectrons?

A laser with a power output of 2.00 mW at a 400-nm wavelength is used to project a beam of light onto a calcium photoelectrode. (a) How many photoelectrons leave the calcium surface per second? (b) What power is carried away by ejected photoelectrons, given that the work function of calcium is 2.31 eV? (c) Calculate the photocurrent. (d) If the photoelectrode suddenly becomes electrically insulated and the setup of two electrodes in the circuit suddenly starts to act like a 2.00-pF capacitor, how long will current flow before the capacitor voltage stops it?

a. $4.02\phantom{\rule{0.2em}{0ex}}×\phantom{\rule{0.2em}{0ex}}{10}^{15};$ b. 0.533 mW; c. 0.644 mA; d. 2.57 ns

The work function for barium is 2.48 eV. Find the maximum kinetic energy of the ejected photoelectrons when the barium surface is illuminated with: (a) radiation emitted by a 100-kW radio station broadcasting at 800 kHz; (b) a 633-nm laser light emitted from a powerful He-Ne laser; and (c) a 434-nm blue light emitted by a small hydrogen gas discharge tube.

(a) Calculate the wavelength of a photon that has the same momentum as a proton moving with 1% of the speed of light in a vacuum. (b) What is the energy of this photon in MeV? (c) What is the kinetic energy of the proton in MeV?

a. 0.132 pm; b. 9.39 MeV; c. 0.047 MeV

(a) Find the momentum of a 100-keV X-ray photon. (b) Find the velocity of a neutron with the same momentum. (c) What is the neutron’s kinetic energy in eV?

The momentum of light, as it is for particles, is exactly reversed when a photon is reflected straight back from a mirror, assuming negligible recoil of the mirror. The change in momentum is twice the photon’s incident momentum, as it is for the particles. Suppose that a beam of light has an intensity $1.0\text{kW}\phantom{\rule{0.1em}{0ex}}\text{/}\phantom{\rule{0.1em}{0ex}}{\text{m}}^{2}$ and falls on a $-2.0{\text{-m}}^{2}$ area of a mirror and reflects from it. (a) Calculate the energy reflected in 1.00 s. (b) What is the momentum imparted to the mirror? (c) Use Newton’s second law to find the force on the mirror. (d) Does the assumption of no-recoil for the mirror seem reasonable?

a. 2 kJ; b. $1.33\phantom{\rule{0.2em}{0ex}}×\phantom{\rule{0.2em}{0ex}}{10}^{\text{−}5}\phantom{\rule{0.2em}{0ex}}\text{kg}·\text{m/s};$ c. $1.33\phantom{\rule{0.2em}{0ex}}×\phantom{\rule{0.2em}{0ex}}{10}^{\text{−}5}\phantom{\rule{0.2em}{0ex}}\text{N};$ d. yes

A photon of energy 5.0 keV collides with a stationary electron and is scattered at an angle of $60\text{°}.$ What is the energy acquired by the electron in the collision?

A 0.75-nm photon is scattered by a stationary electron. The speed of the electron’s recoil is $1.5\phantom{\rule{0.2em}{0ex}}×\phantom{\rule{0.2em}{0ex}}{10}^{6}\text{m/s}.$ (a) Find the wavelength shift of the photon. (b) Find the scattering angle of the photon.

a. 0.003 nm; b. $105.56\text{°}$

Find the maximum change in X-ray wavelength that can occur due to Compton scattering. Does this change depend on the wavelength of the incident beam?

A photon of wavelength 700 nm is incident on a hydrogen atom. When this photon is absorbed, the atom becomes ionized. What is the lowest possible orbit that the electron could have occupied before being ionized?

$n=3$

What is the maximum kinetic energy of an electron such that a collision between the electron and a stationary hydrogen atom in its ground state is definitely elastic?

Singly ionized atomic helium ${\text{He}}^{+1}$ is a hydrogen-like ion. (a) What is its ground-state radius? (b) Calculate the energies of its four lowest energy states. (c) Repeat the calculations for the ${\text{Li}}^{2+}$ ion.

a. ${a}_{0}\phantom{\rule{0.1em}{0ex}}\text{/}\phantom{\rule{0.1em}{0ex}}2;$ b. $-54.4\phantom{\rule{0.2em}{0ex}}\text{eV}\phantom{\rule{0.1em}{0ex}}\text{/}\phantom{\rule{0.1em}{0ex}}{n}^{2};$ c. ${a}_{0}\phantom{\rule{0.1em}{0ex}}\text{/}\phantom{\rule{0.1em}{0ex}}3,-122.4\phantom{\rule{0.2em}{0ex}}\text{eV}\phantom{\rule{0.1em}{0ex}}\text{/}\phantom{\rule{0.1em}{0ex}}{n}^{2}$

A triply ionized atom of beryllium ${\text{Be}}^{3+}$ is a hydrogen-like ion. When ${\text{Be}}^{3+}$ is in one of its excited states, its radius in this nth state is exactly the same as the radius of the first Bohr orbit of hydrogen. Find n and compute the ionization energy for this state of ${\text{Be}}^{3+}.$

In extreme-temperature environments, such as those existing in a solar corona, atoms may be ionized by undergoing collisions with other atoms. One example of such ionization in the solar corona is the presence of ${\text{C}}^{5+}$ ions, detected in the Fraunhofer spectrum. (a) By what factor do the energies of the ${\text{C}}^{5+}$ ion scale compare to the energy spectrum of a hydrogen atom? (b) What is the wavelength of the first line in the Paschen series of ${\text{C}}^{5+}$ ? (c) In what part of the spectrum are these lines located?

a. 36; b. 18.2 nm; c. UV

(a) Calculate the ionization energy for ${\text{He}}^{+}.$ (b) What is the minimum frequency of a photon capable of ionizing ${\text{He}}^{+}$ ?

Experiments are performed with ultracold neutrons having velocities as small as 1.00 m/s. Find the wavelength of such an ultracold neutron and its kinetic energy.

396 nm; 5.23 neV

Find the velocity and kinetic energy of a 6.0-fm neutron. (Rest mass energy of neutron is ${E}_{0}=940\phantom{\rule{0.2em}{0ex}}\text{MeV}\text{.)}$

The spacing between crystalline planes in the NaCl crystal is 0.281 nm, as determined by X-ray diffraction with X-rays of wavelength 0.170 nm. What is the energy of neutrons in the neutron beam that produces diffraction peaks at the same locations as the peaks obtained with the X-rays?

7.3 keV

What is the wavelength of an electron accelerated from rest in a 30.0-kV potential difference?

Calculate the velocity of a $1.0\text{-μ}\text{m}$ electron and a potential difference used to accelerate it from rest to this velocity.

728 m/s; $1.5\mu \text{V}$

In a supercollider at CERN, protons are accelerated to velocities of 0.25c. What are their wavelengths at this speed? What are their kinetic energies? If a beam of protons were to gain its kinetic energy in only one pass through a potential difference, how high would this potential difference have to be? (Rest mass energy of a proton is ${E}_{0}=938\phantom{\rule{0.2em}{0ex}}\text{MeV).}$

Find the de Broglie wavelength of an electron accelerated from rest in an X-ray tube in the potential difference of 100 keV. (Rest mass energy of an electron is ${E}_{0}=511\phantom{\rule{0.2em}{0ex}}\text{keV}\text{.)}$

$\lambda =hc\phantom{\rule{0.1em}{0ex}}\text{/}\phantom{\rule{0.1em}{0ex}}\sqrt{K\left(2{E}_{0}+K\right)}=3.705\phantom{\rule{0.2em}{0ex}}×\phantom{\rule{0.2em}{0ex}}{10}^{\text{−}12}\phantom{\rule{0.2em}{0ex}}\text{m,}\phantom{\rule{0.2em}{0ex}}K=100\phantom{\rule{0.2em}{0ex}}\text{keV}$

The cutoff wavelength for the emission of photoelectrons from a particular surface is 500 nm. Find the maximum kinetic energy of the ejected photoelectrons when the surface is illuminated with light of wavelength 450 nm.

Compare the wavelength shift of a photon scattered by a free electron to that of a photon scattered at the same angle by a free proton.

$\text{Δ}{\lambda }_{c}^{\left(\text{electron}\right)}\phantom{\rule{0.1em}{0ex}}\text{/}\phantom{\rule{0.1em}{0ex}}\text{Δ}{\lambda }_{c}^{\left(\text{proton}\right)}={m}_{p}\phantom{\rule{0.1em}{0ex}}\text{/}\phantom{\rule{0.1em}{0ex}}{m}_{e}=1836$

The spectrometer used to measure the wavelengths of the scattered X-rays in the Compton experiment is accurate to $5.0\phantom{\rule{0.2em}{0ex}}×\phantom{\rule{0.2em}{0ex}}{10}^{-4}\text{nm}.$ What is the minimum scattering angle for which the X-rays interacting with the free electrons can be distinguished from those interacting with the atoms?

Consider a hydrogen-like ion where an electron is orbiting a nucleus that has charge $q=+Ze.$ Derive the formulas for the energy ${E}_{n}$ of the electron in nth orbit and the orbital radius ${r}_{n}.$

(Proof)

Assume that a hydrogen atom exists in the $n=2$ excited state for ${10}^{-8}\text{s}$ before decaying to the ground state. How many times does the electron orbit the proton nucleus during this time? How long does it take Earth to orbit the sun this many times?

An atom can be formed when a negative muon is captured by a proton. The muon has the same charge as the electron and a mass 207 times that of the electron. Calculate the frequency of the photon emitted when this atom makes the transition from $n=2$ to the $n=1$ state. Assume that the muon is orbiting a stationary proton.

$5.1\phantom{\rule{0.2em}{0ex}}×\phantom{\rule{0.2em}{0ex}}{10}^{17}\text{Hz}$

Glossary

double-slit interference experiment: Young’s double-slit experiment, which shows the interference of waves

electron microscopy: microscopy that uses electron waves to “see” fine details of nano-size objects

Heisenberg uncertainty principle: sets the limits on precision in simultaneous measurements of momentum and position of a particle

wave-particle duality: particles can behave as waves and radiation can behave as particles

License

Icon for the Creative Commons Attribution 4.0 International License