Holography

Samuel J. Ling; Jeff Sanny; William Moebs

Diffraction

Holography

Samuel J. Ling; Jeff Sanny; and William Moebs

Learning Objectives

By the end of this section, you will be able to:

Describe how a three-dimensional image is recorded as a hologram
Describe how a three-dimensional image is formed from a hologram

A hologram, such as the one in (Figure), is a true three-dimensional image recorded on film by lasers. Holograms are used for amusement; decoration on novelty items and magazine covers; security on credit cards and driver’s licenses (a laser and other equipment are needed to reproduce them); and for serious three-dimensional information storage. You can see that a hologram is a true three-dimensional image because objects change relative position in the image when viewed from different angles.

Credit cards commonly have holograms for logos, making them difficult to reproduce. (credit: Dominic Alves)

Photograph of a hologram on a credit card. It is in the shape of a bird and reflects many colours.

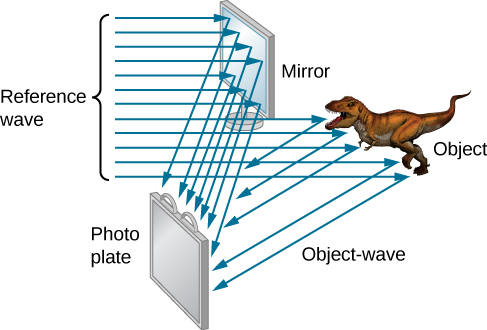
The name hologram means “entire picture” (from the Greek holo, as in holistic) because the image is three-dimensional. Holography is the process of producing holograms and, although they are recorded on photographic film, the process is quite different from normal photography. Holography uses light interference or wave optics, whereas normal photography uses geometric optics. (Figure) shows one method of producing a hologram. Coherent light from a laser is split by a mirror, with part of the light illuminating the object. The remainder, called the reference beam, shines directly on a piece of film. Light scattered from the object interferes with the reference beam, producing constructive and destructive interference. As a result, the exposed film looks foggy, but close examination reveals a complicated interference pattern stored on it. Where the interference was constructive, the film (a negative actually) is darkened. Holography is sometimes called lens-less photography, because it uses the wave characteristics of light, as contrasted to normal photography, which uses geometric optics and requires lenses.

Production of a hologram. Single-wavelength coherent light from a laser produces a well-defined interference pattern on a piece of film. The laser beam is split by a partially silvered mirror, with part of the light illuminating the object and the remainder shining directly on the film. (credit: modification of work by Mariana Ruiz Villarreal)

A mirror at the top faces left and a photo plate at the bottom faces right. A dinosaur labeled object is below the mirror, to the right. Parallel rays labeled reference wave enter from the left. Some fall on the mirror and are reflected to the photo plate. Some fall on the object are are reflected to the photo plate. The latter are labeled object wave.

Light falling on a hologram can form a three-dimensional image of the original object. The process is complicated in detail, but the basics can be understood, as shown in (Figure), in which a laser of the same type that exposed the film is now used to illuminate it. The myriad tiny exposed regions of the film are dark and block the light, whereas less exposed regions allow light to pass. The film thus acts much like a collection of diffraction gratings with various spacing patterns. Light passing through the hologram is diffracted in various directions, producing both real and virtual images of the object used to expose the film. The interference pattern is the same as that produced by the object. Moving your eye to various places in the interference pattern gives you different perspectives, just as looking directly at the object would. The image thus looks like the object and is three dimensional like the object.

A transmission hologram is one that produces real and virtual images when a laser of the same type as that which exposed the hologram is passed through it. Diffraction from various parts of the film produces the same interference pattern that was produced by the object that was used to expose it. (credit: modification of work by Mariana Ruiz Villarreal)

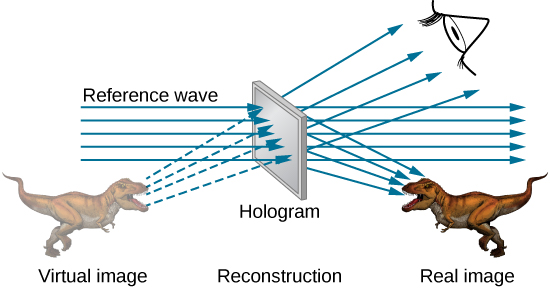
The hologram illustrated in (Figure) is a transmission hologram. Holograms that are viewed with reflected light, such as the white light holograms on credit cards, are reflection holograms and are more common. White light holograms often appear a little blurry with rainbow edges, because the diffraction patterns of various colors of light are at slightly different locations due to their different wavelengths. Further uses of holography include all types of three-dimensional information storage, such as of statues in museums, engineering studies of structures, and images of human organs.

Invented in the late 1940s by Dennis Gabor (1900–1970), who won the 1971 Nobel Prize in Physics for his work, holography became far more practical with the development of the laser. Since lasers produce coherent single-wavelength light, their interference patterns are more pronounced. The precision is so great that it is even possible to record numerous holograms on a single piece of film by just changing the angle of the film for each successive image. This is how the holograms that move as you walk by them are produced—a kind of lens-less movie.

In a similar way, in the medical field, holograms have allowed complete three-dimensional holographic displays of objects from a stack of images. Storing these images for future use is relatively easy. With the use of an endoscope, high-resolution, three-dimensional holographic images of internal organs and tissues can be made.

Summary

Holography is a technique based on wave interference to record and form three-dimensional images.
Lasers offer a practical way to produce sharp holographic images because of their monochromatic and coherent light for pronounced interference patterns.

Key Equations

Destructive interference for a single slit	$D\phantom{\rule{0.2em}{0ex}}\text{sin}\phantom{\rule{0.2em}{0ex}}\theta =m\lambda \phantom{\rule{0.2em}{0ex}}\text{for}\phantom{\rule{0.2em}{0ex}}m=±1,\phantom{\rule{0.2em}{0ex}}±2,\phantom{\rule{0.2em}{0ex}}±3,...$
Half phase angle	$\beta =\frac{\varphi }{2}=\frac{\pi D\phantom{\rule{0.2em}{0ex}}\text{sin}\phantom{\rule{0.2em}{0ex}}\theta }{\lambda }$
Field amplitude in the diffraction pattern	$E=N\text{Δ}{E}_{0}\frac{\text{sin}\phantom{\rule{0.2em}{0ex}}\beta }{\beta }$
Intensity in the diffraction pattern	$I={I}_{0}{\left(\frac{\text{sin}\phantom{\rule{0.2em}{0ex}}\beta }{\beta }\right)}^{2}$
Rayleigh criterion for circular apertures	$\theta =1.22\frac{\lambda }{D}$
Bragg equation	$m\lambda =2d\phantom{\rule{0.2em}{0ex}}\text{sin}\phantom{\rule{0.2em}{0ex}}\theta ,\phantom{\rule{0.2em}{0ex}}m=1,\phantom{\rule{0.2em}{0ex}}2,\phantom{\rule{0.2em}{0ex}}3...$

Conceptual Questions

How can you tell that a hologram is a true three-dimensional image and that those in three-dimensional movies are not?

If a hologram is recorded using monochromatic light at one wavelength but its image is viewed at another wavelength, say $10%$ shorter, what will you see? What if it is viewed using light of exactly half the original wavelength?

Image will appear at slightly different location and/or size when viewed using $10%$ shorter wavelength but at exactly half the wavelength, a higher-order interference reconstructs the original image, different color.

What image will one see if a hologram is recorded using monochromatic light but its image is viewed in white light? Explain.

Additional Problems

White light falls on two narrow slits separated by 0.40 mm. The interference pattern is observed on a screen 3.0 m away. (a) What is the separation between the first maxima for red light $\left(\text{λ}=700\phantom{\rule{0.2em}{0ex}}\text{nm}\right)$ and violet light $\left(\text{λ}=400\phantom{\rule{0.2em}{0ex}}\text{nm}\right)?$ (b) At what point nearest the central maximum will a maximum for yellow light $\left(\text{λ}=600\phantom{\rule{0.2em}{0ex}}\text{nm}\right)$ coincide with a maximum for violet light? Identify the order for each maximum.

a. 2.2 mm; b. $0.172\text{°}$ , second-order yellow and third-order violet coincide

Microwaves of wavelength 10.0 mm fall normally on a metal plate that contains a slit 25 mm wide. (a) Where are the first minima of the diffraction pattern? (b) Would there be minima if the wavelength were 30.0 mm?

Quasars, or quasi-stellar radio sources, are astronomical objects discovered in 1960. They are distant but strong emitters of radio waves with angular size so small, they were originally unresolved, the same as stars. The quasar 3C405 is actually two discrete radio sources that subtend an angle of 82 arcsec. If this object is studied using radio emissions at a frequency of 410 MHz, what is the minimum diameter of a radio telescope that can resolve the two sources?

2.2 km

Two slits each of width 1800 nm and separated by the center-to-center distance of 1200 nm are illuminated by plane waves from a krypton ion laser-emitting at wavelength 461.9 nm. Find the number of interference peaks in the central diffraction peak.

A microwave of an unknown wavelength is incident on a single slit of width 6 cm. The angular width of the central peak is found to be $25\text{°}$ . Find the wavelength.

1.3 cm

Red light (wavelength 632.8 nm in air) from a Helium-Neon laser is incident on a single slit of width 0.05 mm. The entire apparatus is immersed in water of refractive index 1.333. Determine the angular width of the central peak.

A light ray of wavelength 461.9 nm emerges from a 2-mm circular aperture of a krypton ion laser. Due to diffraction, the beam expands as it moves out. How large is the central bright spot at (a) 1 m, (b) 1 km, (c) 1000 km, and (d) at the surface of the moon at a distance of 400,000 km from Earth.

a. 0.28 mm; b. 0.28 m; c. 280 m; d. 113 km

How far apart must two objects be on the moon to be distinguishable by eye if only the diffraction effects of the eye’s pupil limit the resolution? Assume 550 nm for the wavelength of light, the pupil diameter 5.0 mm, and 400,000 km for the distance to the moon.

How far apart must two objects be on the moon to be resolvable by the 8.1-m-diameter Gemini North telescope at Mauna Kea, Hawaii, if only the diffraction effects of the telescope aperture limit the resolution? Assume 550 nm for the wavelength of light and 400,000 km for the distance to the moon.

33 m

A spy satellite is reputed to be able to resolve objects 10. cm apart while operating 197 km above the surface of Earth. What is the diameter of the aperture of the telescope if the resolution is only limited by the diffraction effects? Use 550 nm for light.

Monochromatic light of wavelength 530 nm passes through a horizontal single slit of width $1.5\phantom{\rule{0.2em}{0ex}}\mu \text{m}$ in an opaque plate. A screen of dimensions $2.0\phantom{\rule{0.2em}{0ex}}\text{m}\phantom{\rule{0.2em}{0ex}}×\phantom{\rule{0.2em}{0ex}}2.0\phantom{\rule{0.2em}{0ex}}\text{m}$ is 1.2 m away from the slit. (a) Which way is the diffraction pattern spread out on the screen? (b) What are the angles of the minima with respect to the center? (c) What are the angles of the maxima? (d) How wide is the central bright fringe on the screen? (e) How wide is the next bright fringe on the screen?

a. vertically; b. $±20\text{°}$ , $±44\text{°}$ ; c. 0, $±31\text{°}$ , $±60\text{°}$ ; d. 89 cm; e. 71 cm

A monochromatic light of unknown wavelength is incident on a slit of width $20\phantom{\rule{0.2em}{0ex}}\mu \text{m}$ . A diffraction pattern is seen at a screen 2.5 m away where the central maximum is spread over a distance of 10.0 cm. Find the wavelength.

A source of light having two wavelengths 550 nm and 600 nm of equal intensity is incident on a slit of width $1.8\phantom{\rule{0.2em}{0ex}}\mu \text{m}$ . Find the separation of the $m=1$ bright spots of the two wavelengths on a screen 30.0 cm away.

0.98 cm

A single slit of width 2100 nm is illuminated normally by a wave of wavelength 632.8 nm. Find the phase difference between waves from the top and one third from the bottom of the slit to a point on a screen at a horizontal distance of 2.0 m and vertical distance of 10.0 cm from the center.

A single slit of width $3.0\phantom{\rule{0.2em}{0ex}}\mu \text{m}$ is illuminated by a sodium yellow light of wavelength 589 nm. Find the intensity at a $15\text{°}$ angle to the axis in terms of the intensity of the central maximum.

$I\text{/}{I}_{0}=0.041$

A single slit of width 0.10 mm is illuminated by a mercury lamp of wavelength 576 nm. Find the intensity at a $10\text{°}$ angle to the axis in terms of the intensity of the central maximum.

A diffraction grating produces a second maximum that is 89.7 cm from the central maximum on a screen 2.0 m away. If the grating has 600 lines per centimeter, what is the wavelength of the light that produces the diffraction pattern?

340 nm

A grating with 4000 lines per centimeter is used to diffract light that contains all wavelengths between 400 and 650 nm. How wide is the first-order spectrum on a screen 3.0 m from the grating?

A diffraction grating with 2000 lines per centimeter is used to measure the wavelengths emitted by a hydrogen gas discharge tube. (a) At what angles will you find the maxima of the two first-order blue lines of wavelengths 410 and 434 nm? (b) The maxima of two other first-order lines are found at ${\theta }_{1}=0.097\phantom{\rule{0.2em}{0ex}}\text{rad}$ and ${\theta }_{2}=0.132\phantom{\rule{0.2em}{0ex}}\text{rad}$ . What are the wavelengths of these lines?

a. 0.082 rad and 0.087 rad; b. 480 nm and 660 nm

For white light $\left(400\phantom{\rule{0.2em}{0ex}}\text{nm}\phantom{\rule{0.2em}{0ex}}\text{<}\phantom{\rule{0.2em}{0ex}}\lambda \text{<}\phantom{\rule{0.2em}{0ex}}700\phantom{\rule{0.2em}{0ex}}\text{nm}\right)$ falling normally on a diffraction grating, show that the second and third-order spectra overlap no matter what the grating constant d is.

How many complete orders of the visible spectrum $\left(400\phantom{\rule{0.2em}{0ex}}\text{nm}\phantom{\rule{0.2em}{0ex}}\text{<}\phantom{\rule{0.2em}{0ex}}\lambda \text{<}\phantom{\rule{0.2em}{0ex}}700\phantom{\rule{0.2em}{0ex}}\text{nm}\right)$ can be produced with a diffraction grating that contains 5000 lines per centimeter?

two orders

Two lamps producing light of wavelength 589 nm are ﬁxed 1.0 m apart on a wooden plank. What is the maximum distance an observer can be and still resolve the lamps as two separate sources of light, if the resolution is affected solely by the diffraction of light entering the eye? Assume light enters the eye through a pupil of diameter 4.5 mm.

On a bright clear day, you are at the top of a mountain and looking at a city 12 km away. There are two tall towers 20.0 m apart in the city. Can your eye resolve the two towers if the diameter of the pupil is 4.0 mm? If not, what should be the minimum magniﬁcation power of the telescope needed to resolve the two towers? In your calculations use 550 nm for the wavelength of the light.

yes and N/A

Radio telescopes are telescopes used for the detection of radio emission from space. Because radio waves have much longer wavelengths than visible light, the diameter of a radio telescope must be very large to provide good resolution. For example, the radio telescope in Penticton, BC in Canada, has a diameter of 26 m and can be operated at frequencies as high as 6.6 GHz. (a) What is the wavelength corresponding to this frequency? (b) What is the angular separation of two radio sources that can be resolved by this telescope? (c) Compare the telescope’s resolution with the angular size of the moon.

(credit: modification of work by Jason Nishiyama)

Photograph of a large dish antenna on top of a conical pillar.

Calculate the wavelength of light that produces its first minimum at an angle of $36.9\text{°}$ when falling on a single slit of width $1.00\phantom{\rule{0.2em}{0ex}}\mu \text{m}$ .

600 nm

(a) Find the angle of the third diffraction minimum for 633-nm light falling on a slit of width $20.0\phantom{\rule{0.2em}{0ex}}\mu \text{m}$ . (b) What slit width would place this minimum at $85.0\text{°}$ ?

As an example of diffraction by apertures of everyday dimensions, consider a doorway of width 1.0 m. (a) What is the angular position of the first minimum in the diffraction pattern of 600-nm light? (b) Repeat this calculation for a musical note of frequency 440 Hz (A above middle C). Take the speed of sound to be 343 m/s.

a. $3.4\phantom{\rule{0.2em}{0ex}}×\phantom{\rule{0.2em}{0ex}}{10}^{-5}\text{°}$ ; b. $51\text{°}$

What are the angular positions of the first and second minima in a diffraction pattern produced by a slit of width 0.20 mm that is illuminated by 400 nm light? What is the angular width of the central peak?

How far would you place a screen from the slit of the previous problem so that the second minimum is a distance of 2.5 mm from the center of the diffraction pattern?

0.63 m

How narrow is a slit that produces a diffraction pattern on a screen 1.8 m away whose central peak is 1.0 m wide? Assume $\text{λ}=589\phantom{\rule{0.2em}{0ex}}\text{nm}$ .

Suppose that the central peak of a single-slit diffraction pattern is so wide that the first minima can be assumed to occur at angular positions of $±90\text{°}$ . For this case, what is the ratio of the slit width to the wavelength of the light?

1

The central diffraction peak of the double-slit interference pattern contains exactly nine fringes. What is the ratio of the slit separation to the slit width?

Determine the intensities of three interference peaks other than the central peak in the central maximum of the diffraction, if possible, when a light of wavelength 500 nm is incident normally on a double slit of width 1000 nm and separation 1500 nm. Use the intensity of the central spot to be ${1\phantom{\rule{0.2em}{0ex}}\text{mW/cm}}^{2}$ .

0.17 ${\text{mW/cm}}^{2}$ for $m=1$ only, no higher orders

The yellow light from a sodium vapor lamp seems to be of pure wavelength, but it produces two first-order maxima at $36.093\text{°}$ and $36.129\text{°}$ when projected on a 10,000 line per centimeter diffraction grating. What are the two wavelengths to an accuracy of 0.1 nm?

Structures on a bird feather act like a reflection grating having 8000 lines per centimeter. What is the angle of the first-order maximum for 600-nm light?

$28.7\text{°}$

If a diffraction grating produces a first-order maximum for the shortest wavelength of visible light at $30.0\text{°}$ , at what angle will the first-order maximum be for the largest wavelength of visible light?

(a) What visible wavelength has its fourth-order maximum at an angle of $25.0\text{°}$ when projected on a 25,000-line per centimeter diffraction grating? (b) What is unreasonable about this result? (c) Which assumptions are unreasonable or inconsistent?

a. 42.3 nm; b. This wavelength is not in the visible spectrum. c. The number of slits in this diffraction grating is too large. Etching in integrated circuits can be done to a resolution of 50 nm, so slit separations of 400 nm are at the limit of what we can do today. This line spacing is too small to produce diffraction of light.

Consider a spectrometer based on a diffraction grating. Construct a problem in which you calculate the distance between two wavelengths of electromagnetic radiation in your spectrometer. Among the things to be considered are the wavelengths you wish to be able to distinguish, the number of lines per meter on the diffraction grating, and the distance from the grating to the screen or detector. Discuss the practicality of the device in terms of being able to discern between wavelengths of interest.

An amateur astronomer wants to build a telescope with a diffraction limit that will allow him to see if there are people on the moons of Jupiter. (a) What diameter mirror is needed to be able to see 1.00-m detail on a Jovian moon at a distance of $7.50\phantom{\rule{0.2em}{0ex}}×\phantom{\rule{0.2em}{0ex}}{10}^{8}\phantom{\rule{0.2em}{0ex}}\text{km}$ from Earth? The wavelength of light averages 600 nm. (b) What is unreasonable about this result? (c) Which assumptions are unreasonable or inconsistent?

a. 549 km; b. This is an unreasonably large telescope. c. Unreasonable to assume diffraction limit for optical telescopes unless in space due to atmospheric effects.

Challenge Problems

Blue light of wavelength 450 nm falls on a slit of width 0.25 mm. A converging lens of focal length 20 cm is placed behind the slit and focuses the diffraction pattern on a screen. (a) How far is the screen from the lens? (b) What is the distance between the first and the third minima of the diffraction pattern?

(a) Assume that the maxima are halfway between the minima of a single-slit diffraction pattern. The use the diameter and circumference of the phasor diagram, as described in Intensity in Single-Slit Diffraction, to determine the intensities of the third and fourth maxima in terms of the intensity of the central maximum. (b) Do the same calculation, using (Figure).

a. $\text{I}=0.00500\phantom{\rule{0.2em}{0ex}}{\text{I}}_{0},\phantom{\rule{0.2em}{0ex}}0.00335\phantom{\rule{0.2em}{0ex}}{\text{I}}_{0}$ ; b. $\text{I}=0.00500\phantom{\rule{0.2em}{0ex}}{\text{I}}_{0},\phantom{\rule{0.2em}{0ex}}0.00335\phantom{\rule{0.2em}{0ex}}{\text{I}}_{0}$

(a) By differentiating (Figure), show that the higher-order maxima of the single-slit diffraction pattern occur at values of $\beta$ that satisfy $\text{tan}\phantom{\rule{0.2em}{0ex}}\beta =\beta$ . (b) Plot $y=\text{tan}\phantom{\rule{0.2em}{0ex}}\beta$ and $y=\beta$ versus $\beta$ and find the intersections of these two curves. What information do they give you about the locations of the maxima? (c) Convince yourself that these points do not appear exactly at $\beta =\left(n+\frac{1}{2}\right)\mathrm{\pi ,}$ where $n=0,\phantom{\rule{0.2em}{0ex}}1,\phantom{\rule{0.2em}{0ex}}2,\phantom{\rule{0.2em}{0ex}}\text{…},$ but are quite close to these values.

What is the maximum number of lines per centimeter a diffraction grating can have and produce a complete first-order spectrum for visible light?

12,800

Show that a diffraction grating cannot produce a second-order maximum for a given wavelength of light unless the first-order maximum is at an angle less than $30.0\text{°}$ .

A He-Ne laser beam is reflected from the surface of a CD onto a wall. The brightest spot is the reflected beam at an angle equal to the angle of incidence. However, fringes are also observed. If the wall is 1.50 m from the CD, and the first fringe is 0.600 m from the central maximum, what is the spacing of grooves on the CD?

$1.58\phantom{\rule{0.2em}{0ex}}×\phantom{\rule{0.2em}{0ex}}{10}^{-6}\phantom{\rule{0.2em}{0ex}}\text{m}$

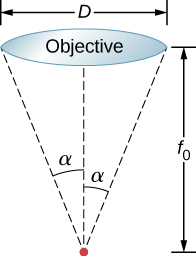
Objects viewed through a microscope are placed very close to the focal point of the objective lens. Show that the minimum separation x of two objects resolvable through the microscope is given by

$x=\frac{1.22\lambda {f}_{0}}{D},$

where ${f}_{0}$ is the focal length and D is the diameter of the objective lens as shown below.

Figure shows an objective lens of diameter D. A point is shown at a distance f subscript 0 from the lens. Two dotted lines connect the point to either end of the lens. These form an angle alpha with the central axis.

Glossary

hologram: three-dimensional image recorded on film by lasers; the word hologram means entire picture (from the Greek word holo, as in holistic)

holography: process of producing holograms with the use of lasers

License

Icon for the Creative Commons Attribution 4.0 International License