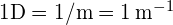The Eye

Samuel J. Ling; Jeff Sanny; William Moebs

Geometric Optics and Image Formation

The Eye

Samuel J. Ling; Jeff Sanny; and William Moebs

Learning Objectives

By the end of this section, you will be able to:

Understand the basic physics of how images are formed by the human eye
Recognize several conditions of impaired vision as well as the optics principles for treating these conditions

The human eye is perhaps the most interesting and important of all optical instruments. Our eyes perform a vast number of functions: They allow us to sense direction, movement, colors, and distance. In this section, we explore the geometric optics of the eye.

Physics of the Eye

The eye is remarkable in how it forms images and in the richness of detail and color it can detect. However, our eyes often need some correction to reach what is called “normal” vision. Actually, normal vision should be called “ideal” vision because nearly one-half of the human population requires some sort of eyesight correction, so requiring glasses is by no means “abnormal.” Image formation by our eyes and common vision correction can be analyzed with the optics discussed earlier in this chapter.

(Figure) shows the basic anatomy of the eye. The cornea and lens form a system that, to a good approximation, acts as a single thin lens. For clear vision, a real image must be projected onto the light-sensitive retina, which lies a fixed distance from the lens. The flexible lens of the eye allows it to adjust the radius of curvature of the lens to produce an image on the retina for objects at different distances. The center of the image falls on the fovea, which has the greatest density of light receptors and the greatest acuity (sharpness) in the visual field. The variable opening (i.e., the pupil) of the eye, along with chemical adaptation, allows the eye to detect light intensities from the lowest observable to ${10}^{10}$ times greater (without damage). This is an incredible range of detection. Processing of visual nerve impulses begins with interconnections in the retina and continues in the brain. The optic nerve conveys the signals received by the eye to the brain.

The cornea and lens of the eye act together to form a real image on the light-sensing retina, which has its densest concentration of receptors in the fovea and a blind spot over the optic nerve. The radius of curvature of the lens of an eye is adjustable to form an image on the retina for different object distances. Layers of tissues with varying indices of refraction in the lens are shown here. However, they have been omitted from other pictures for clarity.

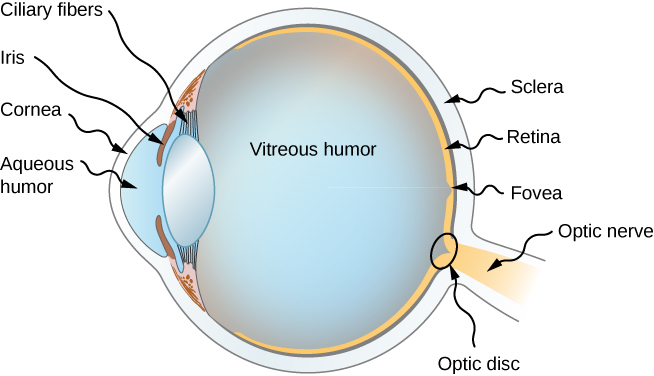
The indices of refraction in the eye are crucial to its ability to form images. (Figure) lists the indices of refraction relevant to the eye. The biggest change in the index of refraction, which is where the light rays are most bent, occurs at the air-cornea interface rather than at the aqueous humor-lens interface. The ray diagram in (Figure) shows image formation by the cornea and lens of the eye. The cornea, which is itself a converging lens with a focal length of approximately 2.3 cm, provides most of the focusing power of the eye. The lens, which is a converging lens with a focal length of about 6.4 cm, provides the finer focus needed to produce a clear image on the retina. The cornea and lens can be treated as a single thin lens, even though the light rays pass through several layers of material (such as cornea, aqueous humor, several layers in the lens, and vitreous humor), changing direction at each interface. The image formed is much like the one produced by a single convex lens (i.e., a real, inverted image). Although images formed in the eye are inverted, the brain inverts them once more to make them seem upright.

Refractive Indices Relevant to the Eye*This is an average value. The actual index of refraction varies throughout the lens and is greatest in center of the lens.
Material	Index of Refraction
Water	1.33
Air	1.0
Cornea	1.38
Aqueous humor	1.34
Lens	1.41^*
Vitreous humor	1.34

In the human eye, an image forms on the retina. Rays from the top and bottom of the object are traced to show how a real, inverted image is produced on the retina. The distance to the object is not to scale.

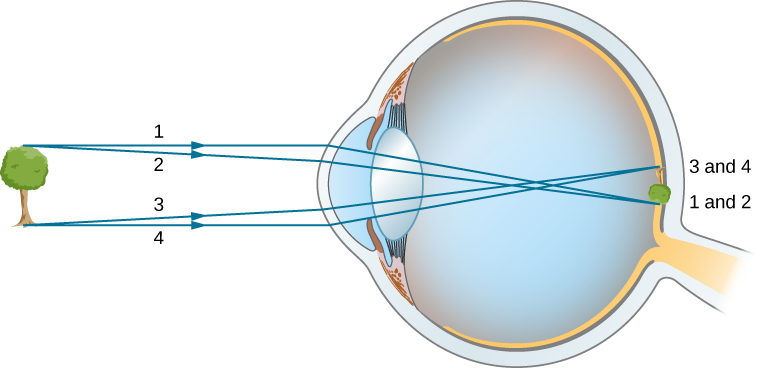
$Figure shows a tree in front of an eye. Rays from the top and bottom of the tree strike the cornea of the eye. They are refracted, intersect in the middle of the vitreous humor and reach the retina. The image formed on the retina is tiny and inverted.$

As noted, the image must fall precisely on the retina to produce clear vision—that is, the image distance ${d}_{\text{i}}$ must equal the lens-to-retina distance. Because the lens-to-retina distance does not change, the image distance ${d}_{\text{i}}$ must be the same for objects at all distances. The ciliary muscles adjust the shape of the eye lens for focusing on nearby or far objects. By changing the shape of the eye lens, the eye changes the focal length of the lens. This mechanism of the eye is called accommodation.

The nearest point an object can be placed so that the eye can form a clear image on the retina is called the near point of the eye. Similarly, the far point is the farthest distance at which an object is clearly visible. A person with normal vision can see objects clearly at distances ranging from 25 cm to essentially infinity. The near point increases with age, becoming several meters for some older people. In this text, we consider the near point to be 25 cm.

We can use the thin-lens equations to quantitatively examine image formation by the eye. First, we define the optical power of a lens as

$P=\frac{1}{f}$

with the focal length f given in meters. The units of optical power are called “diopters” (D). That is, $1\phantom{\rule{0.2em}{0ex}}\text{D}=\frac{1}{\text{m}},\phantom{\rule{0.2em}{0ex}}\text{or}\phantom{\rule{0.2em}{0ex}}1{\phantom{\rule{0.2em}{0ex}}\text{m}}^{-1}$ . Optometrists prescribe common eyeglasses and contact lenses in units of diopters. With this definition of optical power, we can rewrite the thin-lens equations as

$P=\frac{1}{{d}_{\text{o}}}+\frac{1}{{d}_{\text{i}}}.$

Working with optical power is convenient because, for two or more lenses close together, the effective optical power of the lens system is approximately the sum of the optical power of the individual lenses:

${P}_{\mathrm{total}}={P}_{\text{lens}\phantom{\rule{0.2em}{0ex}}1}+{P}_{\text{lens}\phantom{\rule{0.2em}{0ex}}2}+{P}_{\text{lens}\phantom{\rule{0.2em}{0ex}}3}+\text{⋯}$

Effective Focal Length of the Eye The cornea and eye lens have focal lengths of 2.3 and 6.4 cm, respectively. Find the net focal length and optical power of the eye.

Strategy The optical powers of the closely spaced lenses add, so ${P}_{\text{eye}}={P}_{\text{cornea}}+{P}_{\text{lens}}$ .

Solution Writing the equation for power in terms of the focal lengths gives

$\frac{1}{{f}_{\text{eye}}}=\frac{1}{{f}_{\text{cornea}}}+\frac{1}{{f}_{\text{lens}}}=\frac{1}{2.3\phantom{\rule{0.2em}{0ex}}\text{cm}}+\frac{1}{6.4\phantom{\rule{0.2em}{0ex}}\text{cm}}.$

Hence, the focal length of the eye (cornea and lens together) is

${f}_{\text{eye}}=1.69\phantom{\rule{0.2em}{0ex}}\text{cm}.$

The optical power of the eye is

${P}_{\text{eye}}=\frac{1}{{f}_{\text{eye}}}=\frac{1}{0.0169\phantom{\rule{0.2em}{0ex}}\text{m}}=59\phantom{\rule{0.2em}{0ex}}\text{D}.$

For clear vision, the image distance ${d}_{\text{i}}$ must equal the lens-to-retina distance. Normal vision is possible for objects at distances ${d}_{\text{o}}=25\phantom{\rule{0.2em}{0ex}}\text{cm}$ to infinity. The following example shows how to calculate the image distance for an object placed at the near point of the eye.

Image of an object placed at the near point The net focal length of a particular human eye is 1.7 cm. An object is placed at the near point of the eye. How far behind the lens is a focused image formed?

Strategy The near point is 25 cm from the eye, so the object distance is ${d}_{\text{o}}=25\phantom{\rule{0.2em}{0ex}}\text{cm}$ . We determine the image distance from the lens equation:

$\frac{1}{{d}_{\text{i}}}=\frac{1}{f}-\frac{1}{{d}_{\text{o}}}.$

Solution

$\begin{array}{cc}{d}_{\text{i}}\hfill & ={\left(\frac{1}{f}-\frac{1}{{d}_{\text{o}}}\right)}^{-1}\hfill \\ & ={\left(\frac{1}{1.7\phantom{\rule{0.2em}{0ex}}\text{cm}}-\frac{1}{25\phantom{\rule{0.2em}{0ex}}\text{cm}}\right)}^{-1}\hfill \\ & =1.8\phantom{\rule{0.2em}{0ex}}\text{cm}\hfill \end{array}$

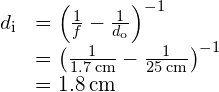
Therefore, the image is formed 1.8 cm behind the lens.

Significance From the magnification formula, we find $m=\text{−}\frac{1.8\phantom{\rule{0.2em}{0ex}}\text{cm}}{25\phantom{\rule{0.2em}{0ex}}\text{cm}}=-0.073$ . Since $m<0$ , the image is inverted in orientation with respect to the object. From the absolute value of m we see that the image is much smaller than the object; in fact, it is only 7% of the size of the object.

Vision Correction

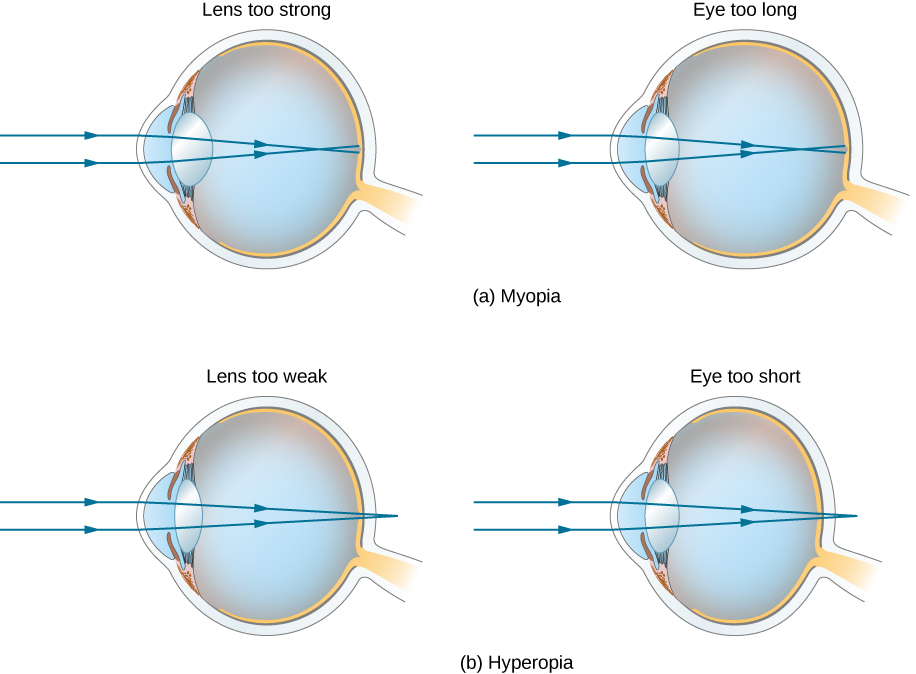
The need for some type of vision correction is very common. Typical vision defects are easy to understand with geometric optics, and some are simple to correct. (Figure) illustrates two common vision defects. Nearsightedness, or myopia, is the ability to see near objects, whereas distant objects are blurry. The eye overconverges the nearly parallel rays from a distant object, and the rays cross in front of the retina. More divergent rays from a close object are converged on the retina for a clear image. The distance to the farthest object that can be seen clearly is called the far point of the eye (normally the far point is at infinity). Farsightedness, or hyperopia, is the ability to see far objects clearly, whereas near objects are blurry. A farsighted eye does not sufficiently converge the rays from a near object to make the rays meet on the retina.

(a) The nearsighted (myopic) eye converges rays from a distant object in front of the retina, so they have diverged when they strike the retina, producing a blurry image. An eye lens that is too powerful can cause nearsightedness, or the eye may be too long. (b) The farsighted (hyperopic) eye is unable to converge the rays from a close object on the retina, producing blurry near-field vision. An eye lens with insufficient optical power or an eye that is too short can cause farsightedness.

Figure a shows two eyes labeled “lens too strong” and “eye too long”. In both cases, parallel rays striking the cornea converge in front of the retina. Figure b shows two eyes labeled “lens too weak” and “eye too short”. In both cases, parallel rays striking the cornea converge behind the retina.

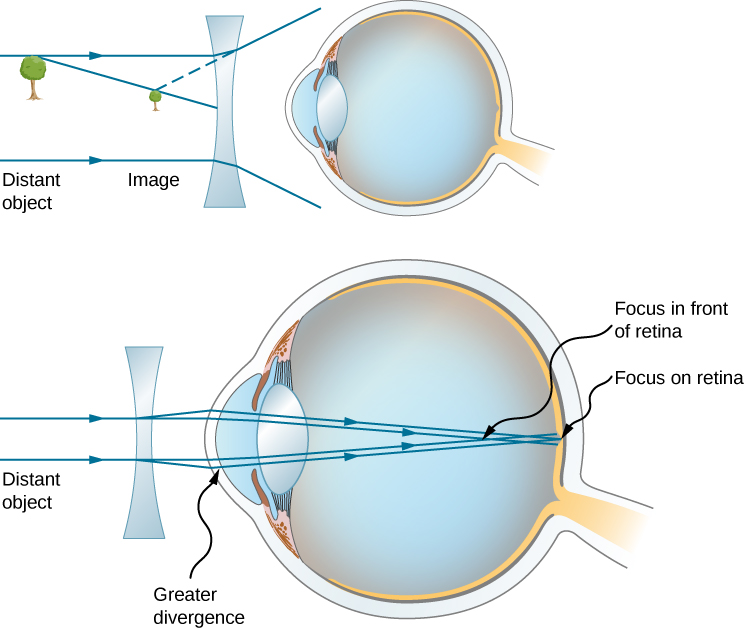
Since the nearsighted eye overconverges light rays, the correction for nearsightedness consists of placing a diverging eyeglass lens in front of the eye, as shown in (Figure). This reduces the optical power of an eye that is too powerful (recall that the focal length of a diverging lens is negative, so its optical power is negative). Another way to understand this correction is that a diverging lens will cause the incoming rays to diverge more to compensate for the excessive convergence caused by the lens system of the eye. The image produced by the diverging eyeglass lens serves as the (optical) object for the eye, and because the eye cannot focus on objects beyond its far point, the diverging lens must form an image of distant (physical) objects at a point that is closer than the far point.

Correction of nearsightedness requires a diverging lens that compensates for overconvergence by the eye. The diverging lens produces an image closer to the eye than the physical object. This image serves as the optical object for the eye, and the nearsighted person can see it clearly because it is closer than their far point.

Figure shows two eyes with a bi-concave lens in front of each. The first one shows a tree as a distant object, and the image of the tree closer to the lens. The second one shows parallel rays from the distant object striking the lens and diverging before they strike the cornea. They then converge on the retina.

Correcting Nearsightedness What optical power of eyeglass lens is needed to correct the vision of a nearsighted person whose far point is 30.0 cm? Assume the corrective lens is fixed 1.50 cm away from the eye.

Strategy You want this nearsighted person to be able to see distant objects clearly, which means that the eyeglass lens must produce an image 30.0 cm from the eye for an object at infinity. An image 30.0 cm from the eye will be $30.0\phantom{\rule{0.2em}{0ex}}\text{cm}-1.50\phantom{\rule{0.2em}{0ex}}\text{cm}=28.5\phantom{\rule{0.2em}{0ex}}\text{cm}$ from the eyeglass lens. Therefore, we must have ${d}_{\text{i}}=-28.5\phantom{\rule{0.2em}{0ex}}\text{cm}$ when ${d}_{\text{o}}=\text{∞}$ . The image distance is negative because it is on the same side of the eyeglass lens as the object.

Solution Since ${d}_{\text{i}}$ and ${d}_{\text{o}}$ are known, we can find the optical power of the eyeglass lens by using (Figure):

$P=\frac{1}{{d}_{\text{o}}}+\frac{1}{{d}_{\text{i}}}=\frac{1}{\text{∞}}+\frac{1}{-0.285\phantom{\rule{0.2em}{0ex}}\text{m}}=-3.51\text{D}.$

Significance The negative optical power indicates a diverging (or concave) lens, as expected. If you examine eyeglasses for nearsighted people, you will find the lenses are thinnest in the center. Additionally, if you examine a prescription for eyeglasses for nearsighted people, you will find that the prescribed optical power is negative and given in units of diopters.

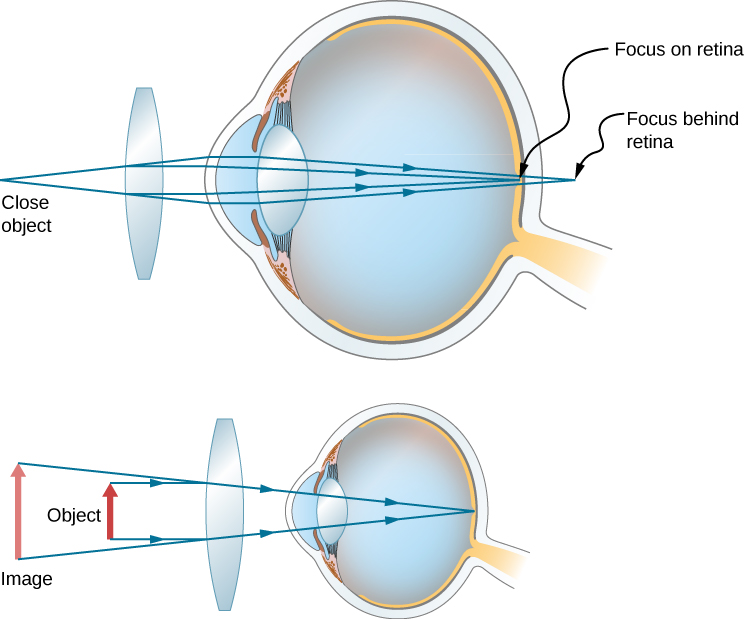
Correcting farsightedness consists simply of using the opposite type of lens as for nearsightedness (i.e., a converging lens), as shown in (Figure).

Such a lens will produce an image of physical objects that are closer than the near point at a distance that is between the near point and the far point, so that the person can see the image clearly. To determine the optical power needed for correction, you must therefore know the person’s near point, as explained in (Figure).

Correction of farsightedness uses a converging lens that compensates for the underconvergence by the eye. The converging lens produces an image farther from the eye than the object, so that the farsighted person can see it clearly.

Figure shows two eyes with a bi-convex lens in front of each. The first one shows rays from a close object striking the lens and deviating towards each other before striking the cornea. They then converge on the retina. The second one shows an object close to the lens and an upright, larger image farther away from the lens.

Correcting Farsightedness What optical power of eyeglass lens is needed to allow a farsighted person, whose near point is 1.00 m, to see an object clearly that is 25.0 cm from the eye? Assume the corrective lens is fixed 1.5 cm from the eye.

Strategy When an object is 25.0 cm from the person’s eyes, the eyeglass lens must produce an image 1.00 m away (the near point), so that the person can see it clearly. An image 1.00 m from the eye will be $100\phantom{\rule{0.2em}{0ex}}\text{cm}-1.5\phantom{\rule{0.2em}{0ex}}\text{cm}=98.5\phantom{\rule{0.2em}{0ex}}\text{cm}$ from the eyeglass lens because the eyeglass lens is 1.5 cm from the eye. Therefore, ${d}_{\text{i}}=-98.5\phantom{\rule{0.2em}{0ex}}\text{cm}$ , where the minus sign indicates that the image is on the same side of the lens as the object. The object is $25.0\phantom{\rule{0.2em}{0ex}}\text{cm}-1.5\phantom{\rule{0.2em}{0ex}}\text{cm}=23.5\phantom{\rule{0.2em}{0ex}}\text{cm}$ from the eyeglass lens, so ${d}_{\text{o}}=23.5\phantom{\rule{0.2em}{0ex}}\text{cm}$ .

Solution Since ${d}_{\text{i}}$ and ${d}_{\text{o}}$ are known, we can find the optical power of the eyeglass lens by using (Figure):

$P=\frac{1}{{d}_{\text{o}}}+\frac{1}{{d}_{\text{i}}}=\frac{1}{0.235\phantom{\rule{0.2em}{0ex}}\text{m}}+\frac{1}{-0.985\phantom{\rule{0.2em}{0ex}}\text{m}}=+3.24\phantom{\rule{0.2em}{0ex}}\text{D}.$

Significance The positive optical power indicates a converging (convex) lens, as expected. If you examine eyeglasses of farsighted people, you will find the lenses to be thickest in the center. In addition, prescription eyeglasses for farsighted people have a prescribed optical power that is positive.

Summary

Image formation by the eye is adequately described by the thin-lens equation.
The eye produces a real image on the retina by adjusting its focal length in a process called accommodation.
Nearsightedness, or myopia, is the inability to see far objects and is corrected with a diverging lens to reduce the optical power of the eye.
Farsightedness, or hyperopia, is the inability to see near objects and is corrected with a converging lens to increase the optical power of the eye.
In myopia and hyperopia, the corrective lenses produce images at distances that fall between the person’s near and far points so that images can be seen clearly.

Conceptual Questions

If the lens of a person’s eye is removed because of cataracts (as has been done since ancient times), why would you expect an eyeglass lens of about 16 D to be prescribed?

When laser light is shone into a relaxed normal-vision eye to repair a tear by spot-welding the retina to the back of the eye, the rays entering the eye must be parallel. Why?

A relaxed, normal-vision eye will focus parallel rays of light onto the retina.

Why is your vision so blurry when you open your eyes while swimming under water? How does a face mask enable clear vision?

It has become common to replace the cataract-clouded lens of the eye with an internal lens. This intraocular lens can be chosen so that the person has perfect distant vision. Will the person be able to read without glasses? If the person was nearsighted, is the power of the intraocular lens greater or less than the removed lens?

A person with an internal lens will need glasses to read because their muscles cannot distort the lens as they do with biological lenses, so they cannot focus on near objects. To correct nearsightedness, the power of the intraocular lens must be less than that of the removed lens.

If the cornea is to be reshaped (this can be done surgically or with contact lenses) to correct myopia, should its curvature be made greater or smaller? Explain.

Problems

Unless otherwise stated, the lens-to-retina distance is 2.00 cm.

What is the power of the eye when viewing an object 50.0 cm away?

$P=52.0\phantom{\rule{0.2em}{0ex}}\text{D}$

Calculate the power of the eye when viewing an object 3.00 m away.

The print in many books averages 3.50 mm in height. How high is the image of the print on the retina when the book is held 30.0 cm from the eye?

$\frac{{h}_{\text{i}}}{{h}_{\text{o}}}=\text{−}\frac{{d}_{\text{i}}}{{d}_{\text{o}}}⇒{h}_{\text{i}}=\text{−}{h}_{\text{o}}\left(\frac{{d}_{\text{i}}}{{d}_{\text{o}}}\right)=\text{−}\left(3.50\phantom{\rule{0.2em}{0ex}}\text{mm}\right)\left(\frac{2.00\phantom{\rule{0.2em}{0ex}}\text{cm}}{30.0\phantom{\rule{0.2em}{0ex}}\text{cm}}\right)=-0.233\phantom{\rule{0.2em}{0ex}}\text{mm}$

Suppose a certain person’s visual acuity is such that he can see objects clearly that form an image $4.00\phantom{\rule{0.2em}{0ex}}\text{μm}$ high on his retina. What is the maximum distance at which he can read the 75.0-cm-high letters on the side of an airplane?

People who do very detailed work close up, such as jewelers, often can see objects clearly at much closer distance than the normal 25 cm. (a) What is the power of the eyes of a woman who can see an object clearly at a distance of only 8.00 cm? (b) What is the image size of a 1.00-mm object, such as lettering inside a ring, held at this distance? (c) What would the size of the image be if the object were held at the normal 25.0 cm distance?

a. $P=+62.5\phantom{\rule{0.2em}{0ex}}\text{D}$ ;
b. $\frac{{h}_{\text{i}}}{{h}_{\text{o}}}=\text{−}\frac{{d}_{\text{i}}}{{d}_{\text{o}}}⇒{h}_{\text{i}}=-0.250\phantom{\rule{0.2em}{0ex}}\text{mm}$ ;
c. ${h}_{\text{i}}=-0.0800\phantom{\rule{0.2em}{0ex}}\text{mm}$

What is the far point of a person whose eyes have a relaxed power of 50.5 D?

What is the near point of a person whose eyes have an accommodated power of 53.5 D?

$P=\frac{1}{{d}_{\text{o}}}+\frac{1}{{d}_{\text{i}}}⇒{d}_{\text{o}}=28.6\phantom{\rule{0.2em}{0ex}}\text{cm}$

(a) A laser reshaping the cornea of a myopic patient reduces the power of his eye by 9.00 D, with a $±5.0%$ uncertainty in the final correction. What is the range of diopters for eyeglass lenses that this person might need after this procedure? (b) Was the person nearsighted or farsighted before the procedure? How do you know?

The power for normal close vision is 54.0 D. In a vision-correction procedure, the power of a patient’s eye is increased by 3.00 D. Assuming that this produces normal close vision, what was the patient’s near point before the procedure?

Originally, the close vision was 51.0 D. Therefore, $P=\frac{1}{{d}_{\text{o}}}+\frac{1}{{d}_{\text{i}}}⇒{d}_{\text{o}}=1.00\phantom{\rule{0.2em}{0ex}}\text{m}$

For normal distant vision, the eye has a power of 50.0 D. What was the previous far point of a patient who had laser vision correction that reduced the power of her eye by 7.00 D, producing normal distant vision?

The power for normal distant vision is 50.0 D. A severely myopic patient has a far point of 5.00 cm. By how many diopters should the power of his eye be reduced in laser vision correction to obtain normal distant vision for him?

originally, $P=70.0\phantom{\rule{0.2em}{0ex}}\text{D}$ ; because the power for normal distant vision is 50.0 D, the power should be decreased by 20.0 D

A student’s eyes, while reading the blackboard, have a power of 51.0 D. How far is the board from his eyes?

The power of a physician’s eyes is 53.0 D while examining a patient. How far from her eyes is the object that is being examined?

$P=\frac{1}{{d}_{\text{o}}}+\frac{1}{{d}_{\text{i}}}⇒{d}_{\text{o}}=0.333\phantom{\rule{0.2em}{0ex}}\text{m}$

The normal power for distant vision is 50.0 D. A young woman with normal distant vision has a 10.0% ability to accommodate (that is, increase) the power of her eyes. What is the closest object she can see clearly?

The far point of a myopic administrator is 50.0 cm. (a) What is the relaxed power of his eyes? (b) If he has the normal 8.00% ability to accommodate, what is the closest object he can see clearly?

a. $P=52.0\phantom{\rule{0.2em}{0ex}}\text{D}$ ;
b. $\begin{array}{c}{P}^{\prime }=56.16\phantom{\rule{0.2em}{0ex}}\text{D}\hfill \\ \\ \frac{1}{{d}_{\text{o}}}+\frac{1}{{d}_{\text{i}}}=P⇒{d}_{\text{o}}=16.2\phantom{\rule{0.2em}{0ex}}\text{cm}\hfill \end{array}$

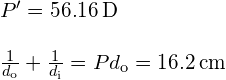
A very myopic man has a far point of 20.0 cm. What power contact lens (when on the eye) will correct his distant vision?

Repeat the previous problem for eyeglasses held 1.50 cm from the eyes.

We need ${d}_{\text{i}}=-18.5\phantom{\rule{0.2em}{0ex}}\text{cm}$ when ${d}_{\text{o}}=\text{∞}$ , so
$P=\text{−}5.41\phantom{\rule{0.2em}{0ex}}\text{D}$

A myopic person sees that her contact lens prescription is –4.00 D. What is her far point?

Repeat the previous problem for glasses that are 1.75 cm from the eyes.

Let $x$ = far point

*** QuickLaTeX cannot compile formula:
\begin{array}{}\\ \\ ⇒P=\frac{1}{-\left(x-0.0175\phantom{\rule{0.2em}{0ex}}\text{m}\right)}+\frac{1}{\text{∞}}⇒-xP+\left(0.0175\phantom{\rule{0.2em}{0ex}}\text{m}\right)P=1\hfill \\ ⇒x=26.8\phantom{\rule{0.2em}{0ex}}\text{cm}\hfill \end{array}

*** Error message:
Missing # inserted in alignment preamble.
leading text: $\begin{array}{}
Unicode character ⇒ (U+21D2)
leading text: $\begin{array}{}\\ \\ ⇒
Missing $ inserted.
leading text: ...\phantom{\rule{0.2em}{0ex}}\text{m}\right)}
Extra }, or forgotten $.
leading text: ...\phantom{\rule{0.2em}{0ex}}\text{m}\right)}
Unicode character ∞ (U+221E)
leading text: ...{0ex}}\text{m}\right)}+\frac{1}{\text{∞}}
Unicode character ⇒ (U+21D2)
leading text: ...x}}\text{m}\right)}+\frac{1}{\text{∞}}⇒
Missing } inserted.
leading text: ...e{0.2em}{0ex}}\text{m}\right)P=1\hfill \\ ⍊Extra }, or forgotten $.
leading text: ...e{0.2em}{0ex}}\text{m}\right)P=1\hfill \\ ⍊Missing } inserted.
leading text: ...e{0.2em}{0ex}}\text{m}\right)P=1\hfill \\ ⍊Extra }, or forgotten $.

The contact lens prescription for a mildly farsighted person is 0.750 D, and the person has a near point of 29.0 cm. What is the power of the tear layer between the cornea and the lens if the correction is ideal, taking the tear layer into account?

Glossary

accommodation: use of the ciliary muscles to adjust the shape of the eye lens for focusing on near or far objects

far point: furthest point an eye can see in focus

farsightedness (or hyperopia): visual defect in which near objects appear blurred because their images are focused behind the retina rather than on the retina; a farsighted person can see far objects clearly but near objects appear blurred

near point: closest point an eye can see in focus

nearsightedness (or myopia): visual defect in which far objects appear blurred because their images are focused in front of the retina rather than on the retina; a nearsighted person can see near objects clearly but far objects appear blurred

optical power: (P) inverse of the focal length of a lens, with the focal length expressed in meters. The optical power P of a lens is expressed in units of diopters D; that is, $1\text{D}=1\text{/m}=1\phantom{\rule{0.2em}{0ex}}{\text{m}}^{-1}$

License

Icon for the Creative Commons Attribution 4.0 International License