Total Internal Reflection

Samuel J. Ling; Jeff Sanny; William Moebs

The Nature of Light

Total Internal Reflection

Samuel J. Ling; Jeff Sanny; and William Moebs

Learning Objectives

By the end of this section, you will be able to:

Explain the phenomenon of total internal reflection
Describe the workings and uses of optical fibers
Analyze the reason for the sparkle of diamonds

A good-quality mirror may reflect more than

*** QuickLaTeX cannot compile formula:
90\text{%}

*** Error message:
File ended while scanning use of \text@.
Emergency stop.

of the light that falls on it, absorbing the rest. But it would be useful to have a mirror that reflects all of the light that falls on it. Interestingly, we can produce total reflection using an aspect of refraction.

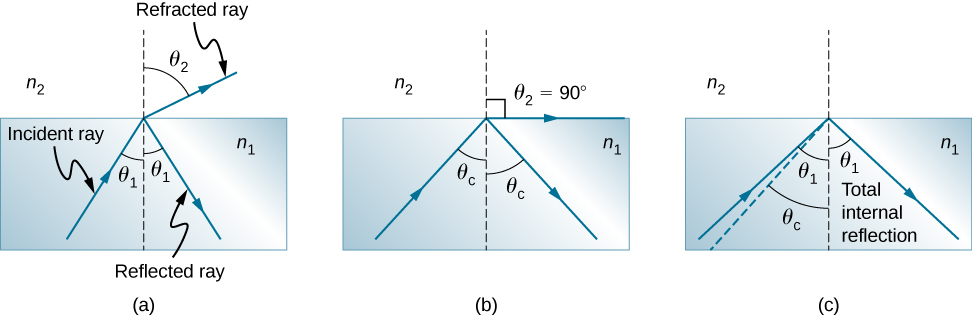
Consider what happens when a ray of light strikes the surface between two materials, as shown in (Figure)(a). Part of the light crosses the boundary and is refracted; the rest is reflected. If, as shown in the figure, the index of refraction for the second medium is less than for the first, the ray bends away from the perpendicular. (Since ${n}_{1}>{n}_{2},$ the angle of refraction is greater than the angle of incidence—that is, ${\theta }_{2}>{\theta }_{1}.\right)$ Now imagine what happens as the incident angle increases. This causes ${\theta }_{2}$ to increase also. The largest the angle of refraction ${\theta }_{2}$ can be is $90\text{°}$ , as shown in part (b). The critical angle ${\theta }_{\text{c}}$ for a combination of materials is defined to be the incident angle ${\theta }_{1}$ that produces an angle of refraction of $90\text{°}$ . That is, ${\theta }_{\text{c}}$ is the incident angle for which ${\theta }_{2}=90\text{°}$ . If the incident angle ${\theta }_{1}$ is greater than the critical angle, as shown in (Figure)(c), then all of the light is reflected back into medium 1, a condition called total internal reflection. (As the figure shows, the reflected rays obey the law of reflection so that the angle of reflection is equal to the angle of incidence in all three cases.)

(a) A ray of light crosses a boundary where the index of refraction decreases. That is, ${n}_{2}<{n}_{1}.$ The ray bends away from the perpendicular. (b) The critical angle ${\theta }_{\text{c}}$ is the angle of incidence for which the angle of refraction is $90\text{°}.$ (c) Total internal reflection occurs when the incident angle is greater than the critical angle.

$In figure a, an incident ray at an angle theta 1 with a perpendicular line drawn at the point of incidence travels from n 1 to n 2. The incident ray undergoes both refraction and reflection. The angle of refraction o the refracted ray in medium n 2 is theta 2. The angle of reflection of the reflected ray in medium 1 is theta 1. In figure b, the incident angle is theta c which is larger than the angle of incidence in figure a. The angle of refraction theta 2 becomes 90 degrees and the angle of reflection is theta c. In figure c, the angle of incidence theta 1 is greater than theta c, total internal reflection takes place and only reflection takes place. The light ray travels back into medium n 1, with the reflection angle being theta one.$

Snell’s law states the relationship between angles and indices of refraction. It is given by

${n}_{1}\phantom{\rule{0.2em}{0ex}}\text{sin}\phantom{\rule{0.2em}{0ex}}{\theta }_{1}={n}_{2}\phantom{\rule{0.2em}{0ex}}\text{sin}\phantom{\rule{0.2em}{0ex}}{\theta }_{2}.$

When the incident angle equals the critical angle $\left({\theta }_{1}={\theta }_{c}\right)$ , the angle of refraction is $90\text{°}$ $\left({\theta }_{2}=90\text{°}\right)$ . Noting that $\text{sin}\phantom{\rule{0.2em}{0ex}}90\text{°}=1,$ Snell’s law in this case becomes

${n}_{1}\phantom{\rule{0.2em}{0ex}}\text{sin}\phantom{\rule{0.2em}{0ex}}{\theta }_{1}={n}_{2}.$

The critical angle ${\theta }_{\text{c}}$ for a given combination of materials is thus

${\theta }_{\text{c}}={\text{sin}}^{-1}\left(\frac{{n}_{2}}{{n}_{1}}\right)\phantom{\rule{0.5em}{0ex}}\text{for}\phantom{\rule{0.2em}{0ex}}{n}_{1}>{n}_{2}.$

Total internal reflection occurs for any incident angle greater than the critical angle ${\theta }_{\text{c}}$ , and it can only occur when the second medium has an index of refraction less than the first. Note that this equation is written for a light ray that travels in medium 1 and reflects from medium 2, as shown in (Figure).

Determining a Critical Angle What is the critical angle for light traveling in a polystyrene (a type of plastic) pipe surrounded by air? The index of refraction for polystyrene is 1.49.

Strategy The index of refraction of air can be taken to be 1.00, as before. Thus, the condition that the second medium (air) has an index of refraction less than the first (plastic) is satisfied, and we can use the equation

${\theta }_{\text{c}}={\text{sin}}^{-1}\left(\frac{{n}_{2}}{{n}_{1}}\right)$

to find the critical angle ${\theta }_{\text{c}},$ where ${n}_{2}=1.00$ and ${n}_{1}=1.49.$

Solution Substituting the identified values gives

${\theta }_{\text{c}}={\text{sin}}^{-1}\left(\frac{1.00}{1.49}\right)={\text{sin}}^{-1}\left(0.671\right)=42.2\text{°}.$

Significance This result means that any ray of light inside the plastic that strikes the surface at an angle greater than $42.2\text{°}$ is totally reflected. This makes the inside surface of the clear plastic a perfect mirror for such rays, without any need for the silvering used on common mirrors. Different combinations of materials have different critical angles, but any combination with ${n}_{1}>{n}_{2}$ can produce total internal reflection. The same calculation as made here shows that the critical angle for a ray going from water to air is $48.6\text{°}$ , whereas that from diamond to air is $24.4\text{°}$ , and that from flint glass to crown glass is $66.3\text{°}$ .

Check Your Understanding At the surface between air and water, light rays can go from air to water and from water to air. For which ray is there no possibility of total internal reflection?

air to water, because the condition that the second medium must have a smaller index of refraction is not satisfied

In the photo that opens this chapter, the image of a swimmer underwater is captured by a camera that is also underwater. The swimmer in the upper half of the photograph, apparently facing upward, is, in fact, a reflected image of the swimmer below. The circular ripple near the photograph’s center is actually on the water surface. The undisturbed water surrounding it makes a good reflecting surface when viewed from below, thanks to total internal reflection. However, at the very top edge of this photograph, rays from below strike the surface with incident angles less than the critical angle, allowing the camera to capture a view of activities on the pool deck above water.

Fiber Optics: Endoscopes to Telephones

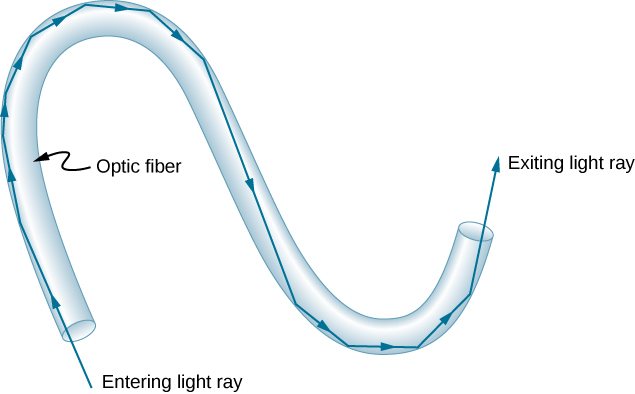
Fiber optics is one application of total internal reflection that is in wide use. In communications, it is used to transmit telephone, internet, and cable TV signals. Fiber optics employs the transmission of light down fibers of plastic or glass. Because the fibers are thin, light entering one is likely to strike the inside surface at an angle greater than the critical angle and, thus, be totally reflected ((Figure)). The index of refraction outside the fiber must be smaller than inside. In fact, most fibers have a varying refractive index to allow more light to be guided along the fiber through total internal refraction. Rays are reflected around corners as shown, making the fibers into tiny light pipes.

Light entering a thin optic fiber may strike the inside surface at large or grazing angles and is completely reflected if these angles exceed the critical angle. Such rays continue down the fiber, even following it around corners, since the angles of reflection and incidence remain large.

Light ray enters an S-shaped optical fiber and undergoes multiple internal reflections at the fiber walls, finally emerging through the other end.

Bundles of fibers can be used to transmit an image without a lens, as illustrated in (Figure). The output of a device called an endoscope is shown in (Figure)(b). Endoscopes are used to explore the interior of the body through its natural orifices or minor incisions. Light is transmitted down one fiber bundle to illuminate internal parts, and the reflected light is transmitted back out through another bundle to be observed.

(a) An image “A” is transmitted by a bundle of optical fibers. (b) An endoscope is used to probe the body, both transmitting light to the interior and returning an image such as the one shown of a human epiglottis (a structure at the base of the tongue). (credit b: modification of work by “Med_Chaos”/Wikimedia Commons)

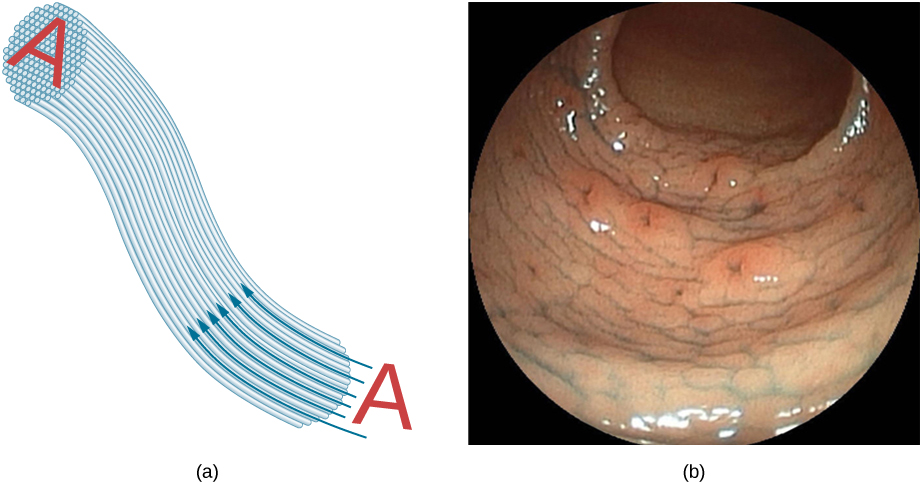
Figure (a) shows how an image A is transmitted through a bundle of parallel fibers. Figure (b) shows an endoscope image.

Fiber optics has revolutionized surgical techniques and observations within the body, with a host of medical diagnostic and therapeutic uses. Surgery can be performed, such as arthroscopic surgery on a knee or shoulder joint, employing cutting tools attached to and observed with the endoscope. Samples can also be obtained, such as by lassoing an intestinal polyp for external examination. The flexibility of the fiber optic bundle allows doctors to navigate it around small and difficult-to-reach regions in the body, such as the intestines, the heart, blood vessels, and joints. Transmission of an intense laser beam to burn away obstructing plaques in major arteries, as well as delivering light to activate chemotherapy drugs, are becoming commonplace. Optical fibers have in fact enabled microsurgery and remote surgery where the incisions are small and the surgeon’s fingers do not need to touch the diseased tissue.

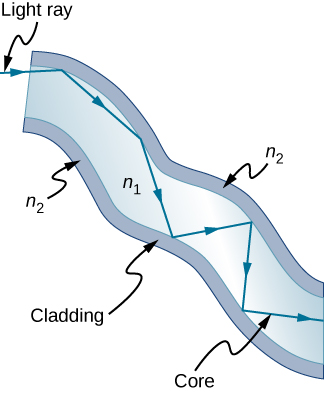
Optical fibers in bundles are surrounded by a cladding material that has a lower index of refraction than the core ((Figure)). The cladding prevents light from being transmitted between fibers in a bundle. Without cladding, light could pass between fibers in contact, since their indices of refraction are identical. Since no light gets into the cladding (there is total internal reflection back into the core), none can be transmitted between clad fibers that are in contact with one another. Instead, the light is propagated along the length of the fiber, minimizing the loss of signal and ensuring that a quality image is formed at the other end. The cladding and an additional protective layer make optical fibers durable as well as flexible.

Fibers in bundles are clad by a material that has a lower index of refraction than the core to ensure total internal reflection, even when fibers are in contact with one another.

$The figure shows a fiber with a medium of refractive index n 1 surrounded by a medium n 2. Medium n sub 2 is made up of cladding material and n sub 1 is the core. The light ray reflects at the interface between the core and the cladding, staying inside the core as it travels along the fiber.$

Special tiny lenses that can be attached to the ends of bundles of fibers have been designed and fabricated. Light emerging from a fiber bundle can be focused through such a lens, imaging a tiny spot. In some cases, the spot can be scanned, allowing quality imaging of a region inside the body. Special minute optical filters inserted at the end of the fiber bundle have the capacity to image the interior of organs located tens of microns below the surface without cutting the surface—an area known as nonintrusive diagnostics. This is particularly useful for determining the extent of cancers in the stomach and bowel.

In another type of application, optical fibers are commonly used to carry signals for telephone conversations and internet communications. Extensive optical fiber cables have been placed on the ocean floor and underground to enable optical communications. Optical fiber communication systems offer several advantages over electrical (copper)-based systems, particularly for long distances. The fibers can be made so transparent that light can travel many kilometers before it becomes dim enough to require amplification—much superior to copper conductors. This property of optical fibers is called low loss. Lasers emit light with characteristics that allow far more conversations in one fiber than are possible with electric signals on a single conductor. This property of optical fibers is called high bandwidth. Optical signals in one fiber do not produce undesirable effects in other adjacent fibers. This property of optical fibers is called reduced crosstalk. We shall explore the unique characteristics of laser radiation in a later chapter.

Corner Reflectors and Diamonds

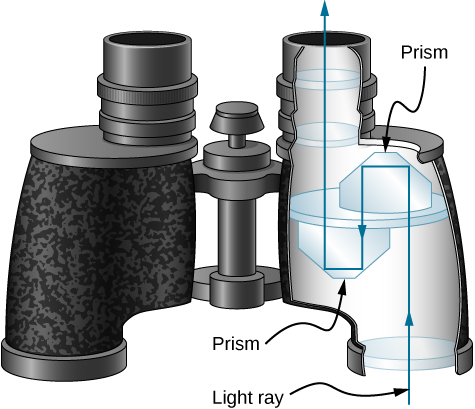
Corner reflectors (The Law of Reflection) are perfectly efficient when the conditions for total internal reflection are satisfied. With common materials, it is easy to obtain a critical angle that is less than $45\text{°}.$ One use of these perfect mirrors is in binoculars, as shown in (Figure). Another use is in periscopes found in submarines.

These binoculars employ corner reflectors (prisms) with total internal reflection to get light to the observer’s eyes.

The figure shows binoculars with prisms inside. The light through one of the object lenses enters through the first prism and undergoes two total internal reflection, exiting parallel to the incident ray but shifted over so it then falls on the second prism. The ray again total internally reflects twice and shifts to emerge out through one of the eyepiece lenses parallel to the incident ray.

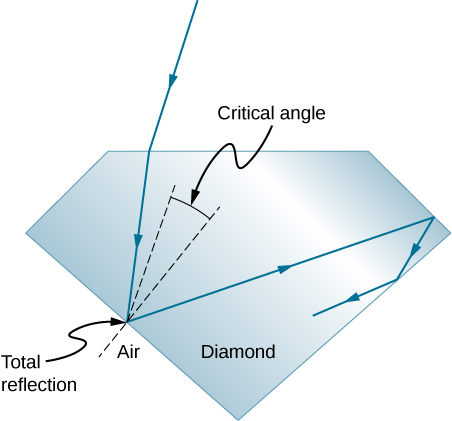
Total internal reflection, coupled with a large index of refraction, explains why diamonds sparkle more than other materials. The critical angle for a diamond-to-air surface is only $24.4\text{°}$ , so when light enters a diamond, it has trouble getting back out ((Figure)). Although light freely enters the diamond, it can exit only if it makes an angle less than $24.4\text{°}$ . Facets on diamonds are specifically intended to make this unlikely. Good diamonds are very clear, so that the light makes many internal reflections and is concentrated before exiting—hence the bright sparkle. (Zircon is a natural gemstone that has an exceptionally large index of refraction, but it is not as large as diamond, so it is not as highly prized. Cubic zirconia is manufactured and has an even higher index of refraction $\left(\text{≈}2.17\right)$ , but it is still less than that of diamond.) The colors you see emerging from a clear diamond are not due to the diamond’s color, which is usually nearly colorless. The colors result from dispersion, which we discuss in Dispersion. Colored diamonds get their color from structural defects of the crystal lattice and the inclusion of minute quantities of graphite and other materials. The Argyle Mine in Western Australia produces around 90% of the world’s pink, red, champagne, and cognac diamonds, whereas around 50% of the world’s clear diamonds come from central and southern Africa.

Light cannot easily escape a diamond, because its critical angle with air is so small. Most reflections are total, and the facets are placed so that light can exit only in particular ways—thus concentrating the light and making the diamond sparkle brightly.

$A light ray falls onto one of the faces of a diamond, gets refracted, falls on another face and gets totally internally reflected since the angle of incidence at the diamond air interface is larger than the critical angle. This reflected ray further undergoes multiple reflections when it falls on other faces.$

Explore refraction and reflection of light between two media with different indices of refraction. Try to make the refracted ray disappear with total internal reflection. Use the protractor tool to measure the critical angle and compare with the prediction from (Figure).

Summary

The incident angle that produces an angle of refraction of $90\text{°}$ is called the critical angle.
Total internal reflection is a phenomenon that occurs at the boundary between two media, such that if the incident angle in the first medium is greater than the critical angle, then all the light is reflected back into that medium.
Fiber optics involves the transmission of light down fibers of plastic or glass, applying the principle of total internal reflection.
Cladding prevents light from being transmitted between fibers in a bundle.
Diamonds sparkle due to total internal reflection coupled with a large index of refraction.

Conceptual Questions

A ring with a colorless gemstone is dropped into water. The gemstone becomes invisible when submerged. Can it be a diamond? Explain.

The gemstone becomes invisible when its index of refraction is the same, or at least similar to, the water surrounding it. Because diamond has a particularly high index of refraction, it can still sparkle as a result of total internal reflection, not invisible.

The most common type of mirage is an illusion that light from faraway objects is reflected by a pool of water that is not really there. Mirages are generally observed in deserts, when there is a hot layer of air near the ground. Given that the refractive index of air is lower for air at higher temperatures, explain how mirages can be formed.

How can you use total internal reflection to estimate the index of refraction of a medium?

One can measure the critical angle by looking for the onset of total internal reflection as the angle of incidence is varied. (Figure) can then be applied to compute the index of refraction.

Problems

Verify that the critical angle for light going from water to air is $48.6\text{°}$ , as discussed at the end of (Figure), regarding the critical angle for light traveling in a polystyrene (a type of plastic) pipe surrounded by air.

(a) At the end of (Figure), it was stated that the critical angle for light going from diamond to air is $24.4\text{°}.$ Verify this. (b) What is the critical angle for light going from zircon to air?

a. $24.42\text{°}$ ; b. $31.33\text{°}$

An optical fiber uses flint glass clad with crown glass. What is the critical angle?

At what minimum angle will you get total internal reflection of light traveling in water and reflected from ice?

$79.11\text{°}$

Suppose you are using total internal reflection to make an efficient corner reflector. If there is air outside and the incident angle is $45.0\text{°}$ , what must be the minimum index of refraction of the material from which the reflector is made?

You can determine the index of refraction of a substance by determining its critical angle. (a) What is the index of refraction of a substance that has a critical angle of $68.4\text{°}$ when submerged in water? What is the substance, based on (Figure)? (b) What would the critical angle be for this substance in air?

a. 1.43, fluorite; b. $44.2\text{°}$

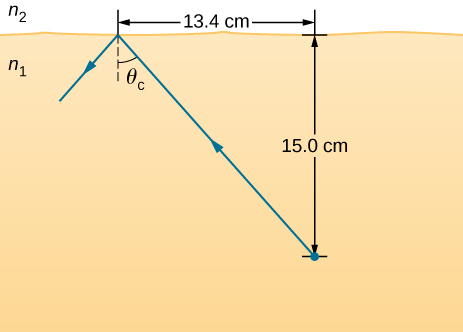
A ray of light, emitted beneath the surface of an unknown liquid with air above it, undergoes total internal reflection as shown below. What is the index of refraction for the liquid and its likely identification?

A light ray travels from an object placed in a medium n 1 at 15.0 centimeters below the horizontal interface with medium n 2. This ray gets totally internally reflected with theta c as critical angle. The horizontal distance between the object and the point of incidence is 13.4 centimeters.

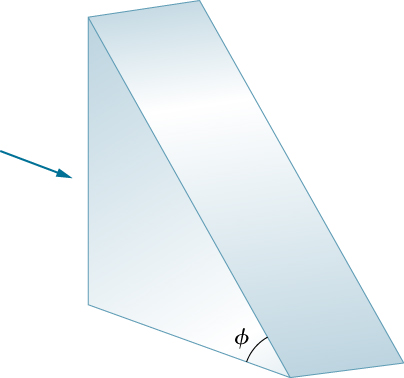
Light rays fall normally on the vertical surface of the glass prism $\left(n=1.50\right)$ shown below. (a) What is the largest value for $\varphi$ such that the ray is totally reflected at the slanted face? (b) Repeat the calculation of part (a) if the prism is immersed in water.

A right angle triangular prism has a horizontal base and a vertical side. The hypotenuse of the triangle makes an angle of phi with the horizontal base. A horizontal light rays is incident normally on the vertical surface of the prism.

a. $48.2\text{°}$ ; b. $27.3\text{°}$

Glossary

critical angle: incident angle that produces an angle of refraction of $90\text{°}$

fiber optics: field of study of the transmission of light down fibers of plastic or glass, applying the principle of total internal reflection

total internal reflection: phenomenon at the boundary between two media such that all the light is reflected and no refraction occurs

License

Icon for the Creative Commons Attribution 4.0 International License