Interference
The Michelson Interferometer
Samuel J. Ling; Jeff Sanny; and William Moebs
Learning Objectives
By the end of this section, you will be able to:
- Explain changes in fringes observed with a Michelson interferometer caused by mirror movements
- Explain changes in fringes observed with a Michelson interferometer caused by changes in medium
The Michelson interferometer (invented by the American physicist Albert A. Michelson, 1852–1931) is a precision instrument that produces interference fringes by splitting a light beam into two parts and then recombining them after they have traveled different optical paths. (Figure) depicts the interferometer and the path of a light beam from a single point on the extended source S, which is a ground-glass plate that diffuses the light from a monochromatic lamp of wavelength ![]() . The beam strikes the half-silvered mirror M, where half of it is reflected to the side and half passes through the mirror. The reflected light travels to the movable plane mirror
. The beam strikes the half-silvered mirror M, where half of it is reflected to the side and half passes through the mirror. The reflected light travels to the movable plane mirror ![]() , where it is reflected back through M to the observer. The transmitted half of the original beam is reflected back by the stationary mirror
, where it is reflected back through M to the observer. The transmitted half of the original beam is reflected back by the stationary mirror ![]() and then toward the observer by M.
and then toward the observer by M.
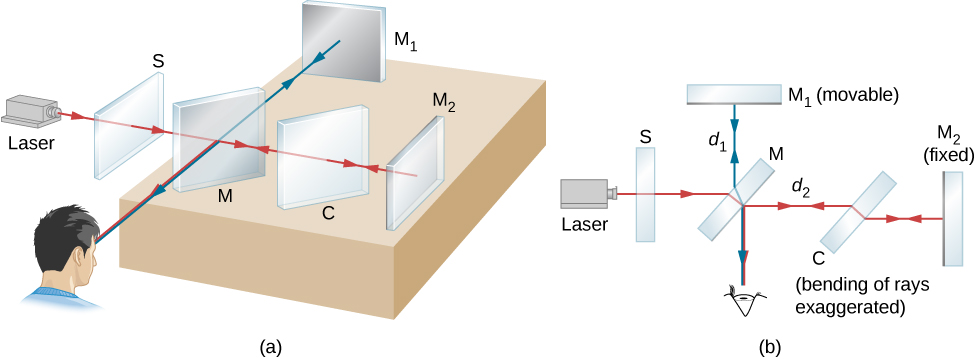
Because both beams originate from the same point on the source, they are coherent and therefore interfere. Notice from the figure that one beam passes through M three times and the other only once. To ensure that both beams traverse the same thickness of glass, a compensator plate C of transparent glass is placed in the arm containing ![]() . This plate is a duplicate of M (without the silvering) and is usually cut from the same piece of glass used to produce M. With the compensator in place, any phase difference between the two beams is due solely to the difference in the distances they travel.
. This plate is a duplicate of M (without the silvering) and is usually cut from the same piece of glass used to produce M. With the compensator in place, any phase difference between the two beams is due solely to the difference in the distances they travel.
The path difference of the two beams when they recombine is ![]() , where
, where ![]() is the distance between M and
is the distance between M and ![]() , and
, and ![]() is the distance between M and
is the distance between M and ![]() . Suppose this path difference is an integer number of wavelengths
. Suppose this path difference is an integer number of wavelengths ![]() . Then, constructive interference occurs and a bright image of the point on the source is seen at the observer. Now the light from any other point on the source whose two beams have this same path difference also undergoes constructive interference and produces a bright image. The collection of these point images is a bright fringe corresponding to a path difference of
. Then, constructive interference occurs and a bright image of the point on the source is seen at the observer. Now the light from any other point on the source whose two beams have this same path difference also undergoes constructive interference and produces a bright image. The collection of these point images is a bright fringe corresponding to a path difference of ![]() ((Figure)). When
((Figure)). When ![]() is moved a distance
is moved a distance ![]() , this path difference changes by
, this path difference changes by ![]() , and each fringe moves to the position previously occupied by an adjacent fringe. Consequently, by counting the number of fringes m passing a given point as
, and each fringe moves to the position previously occupied by an adjacent fringe. Consequently, by counting the number of fringes m passing a given point as ![]() is moved, an observer can measure minute displacements that are accurate to a fraction of a wavelength, as shown by the relation
is moved, an observer can measure minute displacements that are accurate to a fraction of a wavelength, as shown by the relation

Precise Distance Measurements by Michelson Interferometer A red laser light of wavelength 630 nm is used in a Michelson interferometer. While keeping the mirror ![]() fixed, mirror
fixed, mirror ![]() is moved. The fringes are found to move past a fixed cross-hair in the viewer. Find the distance the mirror
is moved. The fringes are found to move past a fixed cross-hair in the viewer. Find the distance the mirror ![]() is moved for a single fringe to move past the reference line.
is moved for a single fringe to move past the reference line.
Strategy Refer to (Figure) for the geometry. We use the result of the Michelson interferometer interference condition to find the distance moved, ![]() .
.
Solution For a 630-nm red laser light, and for each fringe crossing ![]() , the distance traveled by
, the distance traveled by ![]() if you keep
if you keep ![]() fixed is
fixed is
SignificanceAn important application of this measurement is the definition of the standard meter. As mentioned in Units and Measurement, the length of the standard meter was once defined as the mirror displacement in a Michelson interferometer corresponding to 1,650,763.73 wavelengths of the particular fringe of krypton-86 in a gas discharge tube.
Measuring the Refractive Index of a Gas In one arm of a Michelson interferometer, a glass chamber is placed with attachments for evacuating the inside and putting gases in it. The space inside the container is 2 cm wide. Initially, the container is empty. As gas is slowly let into the chamber, you observe that dark fringes move past a reference line in the field of observation. By the time the chamber is filled to the desired pressure, you have counted 122 fringes move past the reference line. The wavelength of the light used is 632.8 nm. What is the refractive index of this gas?
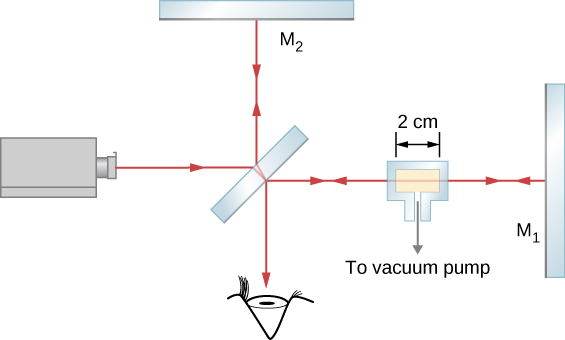
Strategy The ![]() fringes observed compose the difference between the number of wavelengths that fit within the empty chamber (vacuum) and the number of wavelengths that fit within the same chamber when it is gas-filled. The wavelength in the filled chamber is shorter by a factor of n, the index of refraction.
fringes observed compose the difference between the number of wavelengths that fit within the empty chamber (vacuum) and the number of wavelengths that fit within the same chamber when it is gas-filled. The wavelength in the filled chamber is shorter by a factor of n, the index of refraction.
Solution The ray travels a distance ![]() to the right through the glass chamber and another distance t to the left upon reflection. The total travel is
to the right through the glass chamber and another distance t to the left upon reflection. The total travel is ![]() . When empty, the number of wavelengths that fit in this chamber is
. When empty, the number of wavelengths that fit in this chamber is
where ![]() is the wavelength in vacuum of the light used. In any other medium, the wavelength is
is the wavelength in vacuum of the light used. In any other medium, the wavelength is ![]() and the number of wavelengths that fit in the gas-filled chamber is
and the number of wavelengths that fit in the gas-filled chamber is
The number of fringes observed in the transition is
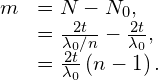
Solving for ![]() gives
gives
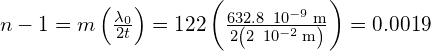
and ![]() .
.
Significance The indices of refraction for gases are so close to that of vacuum, that we normally consider them equal to 1. The difference between 1 and 1.0019 is so small that measuring it requires a correspondingly sensitive technique such as interferometry. We cannot, for example, hope to measure this value using techniques based simply on Snell’s law.
Check Your Understanding Although m, the number of fringes observed, is an integer, which is often regarded as having zero uncertainty, in practical terms, it is all too easy to lose track when counting fringes. In (Figure), if you estimate that you might have missed as many as five fringes when you reported ![]() fringes, (a) is the value for the index of refraction worked out in (Figure) too large or too small? (b) By how much?
fringes, (a) is the value for the index of refraction worked out in (Figure) too large or too small? (b) By how much?
a. too small; b. up to ![]()
Step 1.Examine the situation to determine that interference is involved. Identify whether slits, thin films, or interferometers are considered in the problem.
Step 2.If slits are involved, note that diffraction gratings and double slits produce very similar interference patterns, but that gratings have narrower (sharper) maxima. Single-slit patterns are characterized by a large central maximum and smaller maxima to the sides.
Step 3.If thin-film interference or an interferometer is involved, take note of the path length difference between the two rays that interfere. Be certain to use the wavelength in the medium involved, since it differs from the wavelength in vacuum. Note also that there is an additional ![]() phase shift when light reflects from a medium with a greater index of refraction.
phase shift when light reflects from a medium with a greater index of refraction.
Step 4.Identify exactly what needs to be determined in the problem (identify the unknowns). A written list is useful. Draw a diagram of the situation. Labeling the diagram is useful.
Step 5.Make a list of what is given or can be inferred from the problem as stated (identify the knowns).
Step 6.Solve the appropriate equation for the quantity to be determined (the unknown) and enter the knowns. Slits, gratings, and the Rayleigh limit involve equations.
Step 7.For thin-film interference, you have constructive interference for a total shift that is an integral number of wavelengths. You have destructive interference for a total shift of a half-integral number of wavelengths. Always keep in mind that crest to crest is constructive whereas crest to trough is destructive.
Step 8.Check to see if the answer is reasonable: Does it make sense? Angles in interference patterns cannot be greater than ![]() , for example.
, for example.
Summary
- When the mirror in one arm of the interferometer moves a distance of
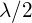 each fringe in the interference pattern moves to the position previously occupied by the adjacent fringe.
each fringe in the interference pattern moves to the position previously occupied by the adjacent fringe.
Key Equations
| Constructive interference | |
| Destructive interference | |
| Path length difference for waves from two slits to a common point on a screen | |
| Constructive interference | |
| Destructive interference | |
| Distance from central maximum to the mth bright fringe | |
| Displacement measured by a Michelson interferometer |
Conceptual Questions
Describe how a Michelson interferometer can be used to measure the index of refraction of a gas (including air).
In one arm, place a transparent chamber to be filled with the gas. See (Figure).
Problems
A Michelson interferometer has two equal arms. A mercury light of wavelength 546 nm is used for the interferometer and stable fringes are found. One of the arms is moved by ![]() . How many fringes will cross the observing field?
. How many fringes will cross the observing field?
What is the distance moved by the traveling mirror of a Michelson interferometer that corresponds to 1500 fringes passing by a point of the observation screen? Assume that the interferometer is illuminated with a 606 nm spectral line of krypton-86.
![]()
When the traveling mirror of a Michelson interferometer is moved ![]() , 90 fringes pass by a point on the observation screen. What is the wavelength of the light used?
, 90 fringes pass by a point on the observation screen. What is the wavelength of the light used?
In a Michelson interferometer, light of wavelength 632.8 nm from a He-Ne laser is used. When one of the mirrors is moved by a distance D, 8 fringes move past the field of view. What is the value of the distance D?
![]()
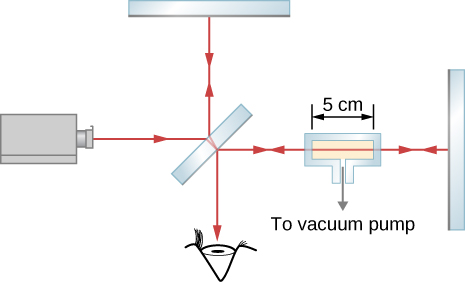
A chamber 5.0 cm long with flat, parallel windows at the ends is placed in one arm of a Michelson interferometer (see below). The light used has a wavelength of 500 nm in a vacuum. While all the air is being pumped out of the chamber, 29 fringes pass by a point on the observation screen. What is the refractive index of the air?
Additional Problems
For 600-nm wavelength light and a slit separation of 0.12 mm, what are the angular positions of the first and third maxima in the double slit interference pattern?
![]()
If the light source in the preceding problem is changed, the angular position of the third maximum is found to be ![]() . What is the wavelength of light being used now?
. What is the wavelength of light being used now?
Red light (![]() ) illuminates double slits separated by a distance
) illuminates double slits separated by a distance ![]() The screen and the slits are 3.00 m apart. (a) Find the distance on the screen between the central maximum and the third maximum. (b) What is the distance between the second and the fourth maxima?
The screen and the slits are 3.00 m apart. (a) Find the distance on the screen between the central maximum and the third maximum. (b) What is the distance between the second and the fourth maxima?
a. 4.26 cm; b. 2.84 cm
Two sources as in phase and emit waves with ![]() . Determine whether constructive or destructive interference occurs at points whose distances from the two sources are (a) 0.84 and 0.42 m, (b) 0.21 and 0.42 m, (c) 1.26 and 0.42 m, (d) 1.87 and 1.45 m, (e) 0.63 and 0.84 m and (f) 1.47 and 1.26 m.
. Determine whether constructive or destructive interference occurs at points whose distances from the two sources are (a) 0.84 and 0.42 m, (b) 0.21 and 0.42 m, (c) 1.26 and 0.42 m, (d) 1.87 and 1.45 m, (e) 0.63 and 0.84 m and (f) 1.47 and 1.26 m.
Two slits ![]() apart are illuminated by light of wavelength 600 nm. What is the highest order fringe in the interference pattern?
apart are illuminated by light of wavelength 600 nm. What is the highest order fringe in the interference pattern?
6
Suppose that the highest order fringe that can be observed is the eighth in a double-slit experiment where 550-nm wavelength light is used. What is the minimum separation of the slits?
The interference pattern of a He-Ne laser light ![]() passing through two slits 0.031 mm apart is projected on a screen 10.0 m away. Determine the distance between the adjacent bright fringes.
passing through two slits 0.031 mm apart is projected on a screen 10.0 m away. Determine the distance between the adjacent bright fringes.
0.20 m
Young’s double-slit experiment is performed immersed in water (![]() ). The light source is a He-Ne laser,
). The light source is a He-Ne laser, ![]() in vacuum. (a) What is the wavelength of this light in water? (b) What is the angle for the third order maximum for two slits separated by 0.100 mm.
in vacuum. (a) What is the wavelength of this light in water? (b) What is the angle for the third order maximum for two slits separated by 0.100 mm.
A double-slit experiment is to be set up so that the bright fringes appear 1.27 cm apart on a screen 2.13 m away from the two slits. The light source was wavelength 500 nm. What should be the separation between the two slits?
0.0839 mm
An effect analogous to two-slit interference can occur with sound waves, instead of light. In an open field, two speakers placed 1.30 m apart are powered by a single-function generator producing sine waves at 1200-Hz frequency. A student walks along a line 12.5 m away and parallel to the line between the speakers. She hears an alternating pattern of loud and quiet, due to constructive and destructive interference. What is (a) the wavelength of this sound and (b) the distance between the central maximum and the first maximum (loud) position along this line?
A hydrogen gas discharge lamp emits visible light at four wavelengths, ![]() 410, 434, 486, and 656 nm. (a) If light from this lamp falls on a N slits separated by 0.025 mm, how far from the central maximum are the third maxima when viewed on a screen 2.0 m from the slits? (b) By what distance are the second and third maxima separated for
410, 434, 486, and 656 nm. (a) If light from this lamp falls on a N slits separated by 0.025 mm, how far from the central maximum are the third maxima when viewed on a screen 2.0 m from the slits? (b) By what distance are the second and third maxima separated for ![]() ?
?
a. 9.8, 10.4, 11.7, and 15.7 cm; b. 3.9 cm
Monochromatic light of frequency ![]() falls on 10 slits separated by 0.020 mm. What is the separation between the first and third maxima on a screen that is 2.0 m from the slits?
falls on 10 slits separated by 0.020 mm. What is the separation between the first and third maxima on a screen that is 2.0 m from the slits?
Eight slits equally separated by 0.149 mm is uniformly illuminated by a monochromatic light at ![]() . What is the width of the central principal maximum on a screen 2.35 m away?
. What is the width of the central principal maximum on a screen 2.35 m away?
![]()
Eight slits equally separated by 0.149 mm is uniformly illuminated by a monochromatic light at ![]() . What is the intensity of a secondary maxima compared to that of the principal maxima?
. What is the intensity of a secondary maxima compared to that of the principal maxima?
A transparent film of thickness 250 nm and index of refraction of 1.40 is surrounded by air. What wavelength in a beam of white light at near-normal incidence to the film undergoes destructive interference when reflected?
700 nm
An intensity minimum is found for 450 nm light transmitted through a transparent film ![]() in air. (a) What is minimum thickness of the film? (b) If this wavelength is the longest for which the intensity minimum occurs, what are the next three lower values of
in air. (a) What is minimum thickness of the film? (b) If this wavelength is the longest for which the intensity minimum occurs, what are the next three lower values of ![]() for which this happens?
for which this happens?
A thin film with ![]() is surrounded by air. What is the minimum thickness of this film such that the reflection of normally incident light with
is surrounded by air. What is the minimum thickness of this film such that the reflection of normally incident light with ![]() is minimized?
is minimized?
189 nm
Repeat your calculation of the previous problem with the thin film placed on a flat glass (![]() ) surface.
) surface.
After a minor oil spill, a think film of oil (![]() ) of thickness 450 nm floats on the water surface in a bay. (a) What predominant color is seen by a bird flying overhead? (b) What predominant color is seen by a seal swimming underwater?
) of thickness 450 nm floats on the water surface in a bay. (a) What predominant color is seen by a bird flying overhead? (b) What predominant color is seen by a seal swimming underwater?
a. green (504 nm); b. magenta (white minus green)
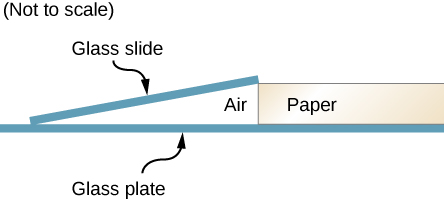
A microscope slide 10 cm long is separated from a glass plate at one end by a sheet of paper. As shown below, the other end of the slide is in contact with the plate. The slide is illuminated from above by light from a sodium lamp (![]() ), and 14 fringes per centimeter are seen along the slide. What is the thickness of the piece of paper?
), and 14 fringes per centimeter are seen along the slide. What is the thickness of the piece of paper?
Suppose that the setup of the preceding problem is immersed in an unknown liquid. If 18 fringes per centimeter are now seen along the slide, what is the index of refraction of the liquid?
1.29
A thin wedge filled with air is produced when two flat glass plates are placed on top of one another and a slip of paper is inserted between them at one edge. Interference fringes are observed when monochromatic light falling vertically on the plates are seen in reflection. Is the first fringe near the edge where the plates are in contact a bright fringe or a dark fringe? Explain.
Two identical pieces of rectangular plate glass are used to measure the thickness of a hair. The glass plates are in direct contact at one edge and a single hair is placed between them hear the opposite edge. When illuminated with a sodium lamp (![]() ), the hair is seen between the 180th and 181st dark fringes. What are the lower and upper limits on the hair’s diameter?
), the hair is seen between the 180th and 181st dark fringes. What are the lower and upper limits on the hair’s diameter?
![]() and
and ![]()
Two microscope slides made of glass are illuminated by monochromatic (![]() ) light incident perpendicularly. The top slide touches the bottom slide at one end and rests on a thin copper wire at the other end, forming a wedge of air. The diameter of the copper wire is
) light incident perpendicularly. The top slide touches the bottom slide at one end and rests on a thin copper wire at the other end, forming a wedge of air. The diameter of the copper wire is ![]() . How many bright fringes are seen across these slides?
. How many bright fringes are seen across these slides?
A good quality camera “lens” is actually a system of lenses, rather than a single lens, but a side effect is that a reflection from the surface of one lens can bounce around many times within the system, creating artifacts in the photograph. To counteract this problem, one of the lenses in such a system is coated with a thin layer of material (![]() ) on one side. The index of refraction of the lens glass is 1.68. What is the smallest thickness of the coating that reduces the reflection at 640 nm by destructive interference? (In other words, the coating’s effect is to be optimized for
) on one side. The index of refraction of the lens glass is 1.68. What is the smallest thickness of the coating that reduces the reflection at 640 nm by destructive interference? (In other words, the coating’s effect is to be optimized for ![]() .)
.)
160 nm
Constructive interference is observed from directly above an oil slick for wavelengths (in air) 440 nm and 616 nm. The index of refraction of this oil is ![]() . What is the film’s minimum possible thickness?
. What is the film’s minimum possible thickness?
A soap bubble is blown outdoors. What colors (indicate by wavelengths) of the reflected sunlight are seen enhanced? The soap bubble has index of refraction 1.36 and thickness 380 nm.
413 nm and 689 nm
A Michelson interferometer with a He-Ne laser light source (![]() ) projects its interference pattern on a screen. If the movable mirror is caused to move by
) projects its interference pattern on a screen. If the movable mirror is caused to move by ![]() , how many fringes will be observed shifting through a reference point on a screen?
, how many fringes will be observed shifting through a reference point on a screen?
An experimenter detects 251 fringes when the movable mirror in a Michelson interferometer is displaced. The light source used is a sodium lamp, wavelength 589 nm. By what distance did the movable mirror move?
![]()
A Michelson interferometer is used to measure the wavelength of light put through it. When the movable mirror is moved by exactly 0.100 mm, the number of fringes observed moving through is 316. What is the wavelength of the light?
A 5.08-cm-long rectangular glass chamber is inserted into one arm of a Michelson interferometer using a 633-nm light source. This chamber is initially filled with air ![]() at standard atmospheric pressure but the air is gradually pumped out using a vacuum pump until a near perfect vacuum is achieved. How many fringes are observed moving by during the transition?
at standard atmospheric pressure but the air is gradually pumped out using a vacuum pump until a near perfect vacuum is achieved. How many fringes are observed moving by during the transition?
47
Into one arm of a Michelson interferometer, a plastic sheet of thickness ![]() is inserted, which causes a shift in the interference pattern by 86 fringes. The light source has wavelength of 610 nm in air. What is the index of refraction of this plastic?
is inserted, which causes a shift in the interference pattern by 86 fringes. The light source has wavelength of 610 nm in air. What is the index of refraction of this plastic?
The thickness of an aluminum foil is measured using a Michelson interferometer that has its movable mirror mounted on a micrometer. There is a difference of 27 fringes in the observed interference pattern when the micrometer clamps down on the foil compared to when the micrometer is empty. Calculate the thickness of the foil?
![]()
The movable mirror of a Michelson interferometer is attached to one end of a thin metal rod of length 23.3 mm. The other end of the rod is anchored so it does not move. As the temperature of the rod changes from ![]() to
to ![]() , a change of 14 fringes is observed. The light source is a He Ne laser,
, a change of 14 fringes is observed. The light source is a He Ne laser, ![]() . What is the change in length of the metal bar, and what is its thermal expansion coefficient?
. What is the change in length of the metal bar, and what is its thermal expansion coefficient?
In a thermally stabilized lab, a Michelson interferometer is used to monitor the temperature to ensure it stays constant. The movable mirror is mounted on the end of a 1.00-m-long aluminum rod, held fixed at the other end. The light source is a He Ne laser, ![]() . The resolution of this apparatus corresponds to the temperature difference when a change of just one fringe is observed. What is this temperature difference?
. The resolution of this apparatus corresponds to the temperature difference when a change of just one fringe is observed. What is this temperature difference?
![]()
A 65-fringe shift results in a Michelson interferometer when a ![]() film made of an unknown material is placed in one arm. The light source has wavelength 632.9 nm. Identify the material using the indices of refraction found in (Figure).
film made of an unknown material is placed in one arm. The light source has wavelength 632.9 nm. Identify the material using the indices of refraction found in (Figure).
Challenge Problems
Determine what happens to the double-slit interference pattern if one of the slits is covered with a thin, transparent film whose thickness is ![]() , where
, where ![]() is the wavelength of the incident light and n is the index of refraction of the film.
is the wavelength of the incident light and n is the index of refraction of the film.
Bright and dark fringes switch places.
Fifty-one narrow slits are equally spaced and separated by 0.10 mm. The slits are illuminated by blue light of wavelength 400 nm. What is angular position of the twenty-fifth secondary maximum? What is its peak intensity in comparison with that of the primary maximum?
A film of oil on water will appear dark when it is very thin, because the path length difference becomes small compared with the wavelength of light and there is a phase shift at the top surface. If it becomes dark when the path length difference is less than one-fourth the wavelength, what is the thickest the oil can be and appear dark at all visible wavelengths? Oil has an index of refraction of 1.40.
The path length must be less than one-fourth of the shortest visible wavelength in oil. The thickness of the oil is half the path length, so it must be less than one-eighth of the shortest visible wavelength in oil. If we take 380 nm to be the shortest visible wavelength in air, 33.9 nm.
(Figure) shows two glass slides illuminated by monochromatic light incident perpendicularly. The top slide touches the bottom slide at one end and rests on a 0.100-mm-diameter hair at the other end, forming a wedge of air. (a) How far apart are the dark bands, if the slides are 7.50 cm long and 589-nm light is used? (b) Is there any difference if the slides are made from crown or flint glass? Explain.
(Figure) shows two 7.50-cm-long glass slides illuminated by pure 589-nm wavelength light incident perpendicularly. The top slide touches the bottom slide at one end and rests on some debris at the other end, forming a wedge of air. How thick is the debris, if the dark bands are 1.00 mm apart?
![]()
A soap bubble is 100 nm thick and illuminated by white light incident at a ![]() angle to its surface. What wavelength and color of visible light is most constructively reflected, assuming the same index of refraction as water?
angle to its surface. What wavelength and color of visible light is most constructively reflected, assuming the same index of refraction as water?
An oil slick on water is 120 nm thick and illuminated by white light incident at a ![]() angle to its surface. What color does the oil appear (what is the most constructively reflected wavelength), given its index of refraction is 1.40?
angle to its surface. What color does the oil appear (what is the most constructively reflected wavelength), given its index of refraction is 1.40?
for one phase change: 950 nm (infrared); for three phase changes: 317 nm (ultraviolet); Therefore, the oil film will appear black, since the reflected light is not in the visible part of the spectrum.
Glossary
- interferometer
- instrument that uses interference of waves to make measurements

