Nuclear Physics
Nuclear Fusion
Samuel J. Ling; Jeff Sanny; and William Moebs
Learning Objectives
By the end of this section, you will be able to:
- Describe the process of nuclear fusion in terms of its product and reactants
- Calculate the energies of particles produced by a fusion reaction
- Explain the fission concept in the context of fusion bombs, the production of energy by the Sun, and nucleosynthesis
The process of combining lighter nuclei to make heavier nuclei is called nuclear fusion. As with fission reactions, fusion reactions are exothermic—they release energy. Suppose that we fuse a carbon and helium nuclei to produce oxygen:
The energy changes in this reaction can be understood using a graph of binding energy per nucleon ((Figure)). Comparing the binding energy per nucleon for oxygen, carbon, and helium, the oxygen nucleus is much more tightly bound than the carbon and helium nuclei, indicating that the reaction produces a drop in the energy of the system. This energy is released in the form of gamma radiation. Fusion reactions are said to be exothermic when the amount of energy released (known as the Q value) in each reaction is greater than zero ![]()
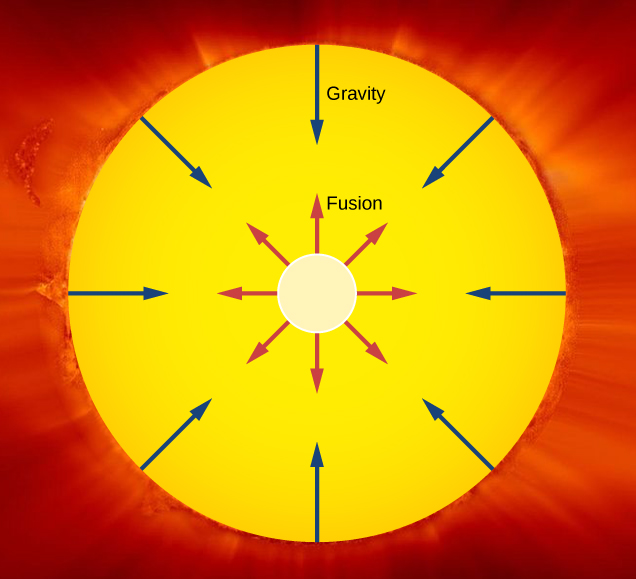
An important example of nuclear fusion in nature is the production of energy in the Sun. In 1938, Hans Bethe proposed that the Sun produces energy when hydrogen nuclei (![]() ) fuse into stable helium nuclei
) fuse into stable helium nuclei ![]() in the Sun’s core ((Figure)). This process, called the proton-proton chain, is summarized by three reactions:
in the Sun’s core ((Figure)). This process, called the proton-proton chain, is summarized by three reactions:
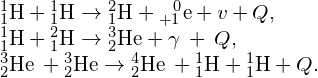
Thus, a stable helium nucleus is formed from the fusion of the nuclei of the hydrogen atom. These three reactions can be summarized by
The net Q value is about 26 MeV. The release of this energy produces an outward thermal gas pressure that prevents the Sun from gravitational collapse. Astrophysicists find that hydrogen fusion supplies the energy stars require to maintain energy balance over most of a star’s life span.
Nucleosynthesis
Scientist now believe that many heavy elements found on Earth and throughout the universe were originally synthesized by fusion within the hot cores of the stars. This process is known as nucleosynthesis. For example, in lighter stars, hydrogen combines to form helium through the proton-proton chain. Once the hydrogen fuel is exhausted, the star enters the next stage of its life and fuses helium. An example of a nuclear reaction chain that can occur is:
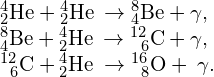
Carbon and oxygen nuclei produced in such processes eventually reach the star’s surface by convection. Near the end of its lifetime, the star loses its outer layers into space, thus enriching the interstellar medium with the nuclei of heavier elements ((Figure)).
Stars similar in mass to the Sun do not become hot enough to fuse nuclei as heavy (or heavier) than oxygen nuclei. However, in massive stars whose cores become much hotter ![]() even more complex nuclei are produced. Some representative reactions are
even more complex nuclei are produced. Some representative reactions are
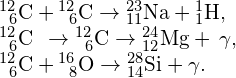
Nucleosynthesis continues until the core is primarily iron-nickel metal. Now, iron has the peculiar property that any fusion or fission reaction involving the iron nucleus is endothermic, meaning that energy is absorbed rather than produced. Hence, nuclear energy cannot be generated in an iron-rich core. Lacking an outward pressure from fusion reactions, the star begins to contract due to gravity. This process heats the core to a temperature on the order of ![]() Expanding shock waves generated within the star due to the collapse cause the star to quickly explode. The luminosity of the star can increase temporarily to nearly that of an entire galaxy. During this event, the flood of energetic neutrons reacts with iron and the other nuclei to produce elements heavier than iron. These elements, along with much of the star, are ejected into space by the explosion. Supernovae and the formation of planetary nebulas together play a major role in the dispersal of chemical elements into space.
Expanding shock waves generated within the star due to the collapse cause the star to quickly explode. The luminosity of the star can increase temporarily to nearly that of an entire galaxy. During this event, the flood of energetic neutrons reacts with iron and the other nuclei to produce elements heavier than iron. These elements, along with much of the star, are ejected into space by the explosion. Supernovae and the formation of planetary nebulas together play a major role in the dispersal of chemical elements into space.
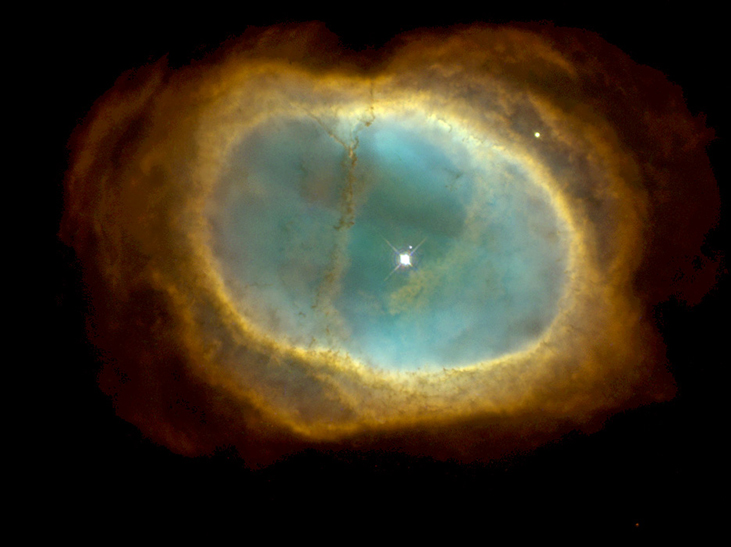
Eventually, much of the material lost by stars is pulled together through the gravitational force, and it condenses into a new generation of stars and accompanying planets. Recent images from the Hubble Space Telescope provide a glimpse of this magnificent process taking place in the constellation Serpens ((Figure)). The new generation of stars begins the nucleosynthesis process anew, with a higher percentage of heavier elements. Thus, stars are “factories” for the chemical elements, and many of the atoms in our bodies were once a part of stars.

Energy of the Sun The power output of the Sun is approximately ![]() Most of this energy is produced in the Sun’s core by the proton-proton chain. This energy is transmitted outward by the processes of convection and radiation. (a) How many of these fusion reactions per second must occur to supply the power radiated by the Sun? (b) What is the rate at which the mass of the Sun decreases? (c) In about five billion years, the central core of the Sun will be depleted of hydrogen. By what percentage will the mass of the Sun have decreased from its present value when the core is depleted of hydrogen?
Most of this energy is produced in the Sun’s core by the proton-proton chain. This energy is transmitted outward by the processes of convection and radiation. (a) How many of these fusion reactions per second must occur to supply the power radiated by the Sun? (b) What is the rate at which the mass of the Sun decreases? (c) In about five billion years, the central core of the Sun will be depleted of hydrogen. By what percentage will the mass of the Sun have decreased from its present value when the core is depleted of hydrogen?
Strategy The total energy output per second is given in the problem statement. If we know the energy released in each fusion reaction, we can determine the rate of the fusion reactions. If the mass loss per fusion reaction is known, the mass loss rate is known. Multiplying this rate by five billion years gives the total mass lost by the Sun. This value is divided by the original mass of the Sun to determine the percentage of the Sun’s mass that has been lost when the hydrogen fuel is depleted.
Solution
- The decrease in mass for the fusion reaction is
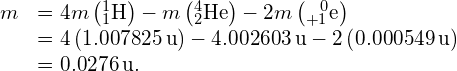
The energy released per fusion reaction is
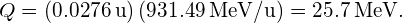
Thus, to supply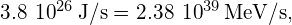 there must be
there must be
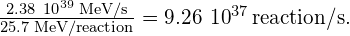
- The Sun’s mass decreases by
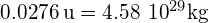 per fusion reaction, so the rate at which its mass decreases is
per fusion reaction, so the rate at which its mass decreases is
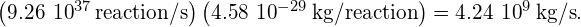
- In
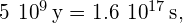 the Sun’s mass will therefore decrease by
the Sun’s mass will therefore decrease by
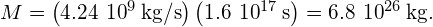
The current mass of the Sun is about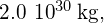 so the percentage decrease in its mass when its hydrogen fuel is depleted will be
so the percentage decrease in its mass when its hydrogen fuel is depleted will be
*** QuickLaTeX cannot compile formula: \left(\frac{6.8\phantom{\rule{0.2em}{0ex}}×\phantom{\rule{0.2em}{0ex}}{10}^{26}\phantom{\rule{0.2em}{0ex}}\text{kg}}{2.0\phantom{\rule{0.2em}{0ex}}×\phantom{\rule{0.2em}{0ex}}{10}^{30}\phantom{\rule{0.2em}{0ex}}\text{kg}}\right)\phantom{\rule{0.2em}{0ex}}×\phantom{\rule{0.2em}{0ex}}100\text{%}=0.034\text{%}. *** Error message: File ended while scanning use of \text@. Emergency stop.
Significance After five billion years, the Sun is very nearly the same mass as it is now. Hydrogen burning does very little to change the mass of the Sun. This calculation assumes that only the proton-proton decay change is responsible for the power output of the Sun.
Check Your Understanding Where does the energy from the Sun originate?
the conversion of mass to energy
The Hydrogen Bomb
In 1942, Robert Oppenheimer suggested that the extremely high temperature of an atomic bomb could be used to trigger a fusion reaction between deuterium and tritium, thus producing a fusion (or hydrogen) bomb. The reaction between deuterium and tritium, both isotopes of hydrogen, is given by
Deuterium is relatively abundant in ocean water but tritium is scarce. However, tritium can be generated in a nuclear reactor through a reaction involving lithium. The neutrons from the reactor cause the reaction
to produce the desired tritium. The first hydrogen bomb was detonated in 1952 on the remote island of Eniwetok in the Marshall Islands. A hydrogen bomb has never been used in war. Modern hydrogen bombs are approximately 1000 times more powerful than the fission bombs dropped on Hiroshima and Nagasaki in World War II.
The Fusion Reactor
The fusion chain believed to be the most practical for use in a nuclear fusion reactor is the following two-step process:
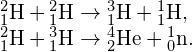
This chain, like the proton-proton chain, produces energy without any radioactive by-product. However, there is a very difficult problem that must be overcome before fusion can be used to produce significant amounts of energy: Extremely high temperatures ![]() are needed to drive the fusion process. To meet this challenge, test fusion reactors are being developed to withstand temperatures 20 times greater than the Sun’s core temperature. An example is the Joint European Torus (JET) shown in (Figure). A great deal of work still has to be done on fusion reactor technology, but many scientists predict that fusion energy will power the world’s cities by the end of the twentieth century.
are needed to drive the fusion process. To meet this challenge, test fusion reactors are being developed to withstand temperatures 20 times greater than the Sun’s core temperature. An example is the Joint European Torus (JET) shown in (Figure). A great deal of work still has to be done on fusion reactor technology, but many scientists predict that fusion energy will power the world’s cities by the end of the twentieth century.

Summary
- Nuclear fusion is a reaction in which two nuclei are combined to form a larger nucleus; energy is released when light nuclei are fused to form medium-mass nuclei.
- The amount of energy released by a fusion reaction is known as the Q value.
- Nuclear fusion explains the reaction between deuterium and tritium that produces a fusion (or hydrogen) bomb; fusion also explains the production of energy in the Sun, the process of nucleosynthesis, and the creation of the heavy elements.
Conceptual Questions
Explain the difference between nuclear fission and nuclear fusion.
Why does the fusion of light nuclei into heavier nuclei release energy?
The nuclei produced in the fusion process have a larger binding energy per nucleon than the nuclei that are fused. That is, nuclear fusion decreases average energy of the nucleons in the system. The energy difference is carried away as radiation.
Problems
Verify that the total number of nucleons, and total charge are conserved for each of the following fusion reactions in the proton-proton chain.
(i) ![]() ,
,
(ii) ![]() , and (iii)
, and (iii) ![]() .
.
(List the value of each of the conserved quantities before and after each of the reactions.)
i. 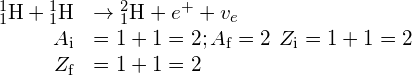 ;
;
ii. 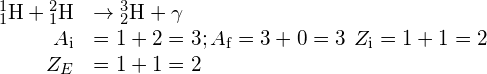 ;
;
iii. 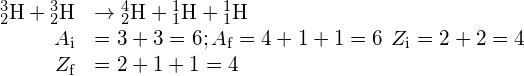
Calculate the energy output in each of the fusion reactions in the proton-proton chain, and verify the values determined in the preceding problem.
Show that the total energy released in the proton-proton chain is 26.7 MeV, considering the overall effect in ![]() ,
, ![]() , and
, and ![]() . Be sure to include the annihilation energy.
. Be sure to include the annihilation energy.
26.73 MeV
Two fusion reactions mentioned in the text are ![]() and
and ![]() . Both reactions release energy, but the second also creates more fuel. Confirm that the energies produced in the reactions are 20.58 and 2.22 MeV, respectively. Comment on which product nuclide is most tightly bound,
. Both reactions release energy, but the second also creates more fuel. Confirm that the energies produced in the reactions are 20.58 and 2.22 MeV, respectively. Comment on which product nuclide is most tightly bound, ![]() or
or ![]() .
.
The power output of the Sun is ![]() (a) If
(a) If
*** QuickLaTeX cannot compile formula:
90\text{%}
*** Error message:
File ended while scanning use of \text@.
Emergency stop.
of this energy is supplied by the proton-proton chain, how many protons are consumed per second? (b) How many neutrinos per second should there be per square meter at the surface of Earth from this process?
a. ![]() ; b.
; b. ![]() ;
;
This huge number is indicative of how rarely a neutrino interacts, since large detectors observe very few per day.
Another set of reactions that fuses hydrogen into helium in the Sun and especially in hotter stars is called the CNO cycle:
![]()
![]()
![]()
![]()
![]()
![]()
This process is a “cycle” because ![]() appears at the beginning and end of these reactions. Write down the overall effect of this cycle (as done for the proton-proton chain in
appears at the beginning and end of these reactions. Write down the overall effect of this cycle (as done for the proton-proton chain in ![]() ). Assume that the positrons annihilate electrons to form more
). Assume that the positrons annihilate electrons to form more ![]() rays.
rays.
(a) Calculate the energy released by the fusion of a 1.00-kg mixture of deuterium and tritium, which produces helium. There are equal numbers of deuterium and tritium nuclei in the mixture.
(b) If this process takes place continuously over a period of a year, what is the average power output?
a. The atomic mass of deuterium (![]() ) is 2.014102 u, while that of tritium (
) is 2.014102 u, while that of tritium (![]() ) is 3.016049 u, for a total of 5.032151 u per reaction. So a mole of reactants has a mass of 5.03 g, and in 1.00 kg, there are
) is 3.016049 u, for a total of 5.032151 u per reaction. So a mole of reactants has a mass of 5.03 g, and in 1.00 kg, there are ![]() of reactants. The number of reactions that take place is therefore
of reactants. The number of reactions that take place is therefore
![]() .
.
The total energy output is the number of reactions times the energy per reaction:
![]()
b. Power is energy per unit time. One year has ![]() so
so
![]()
We expect nuclear processes to yield large amounts of energy, and this is certainly the case here. The energy output of ![]() from fusing 1.00 kg of deuterium and tritium is equivalent to 2.6 million gallons of gasoline and about eight times the energy output of the bomb that destroyed Hiroshima. Yet the average backyard swimming pool has about 6 kg of deuterium in it, so that fuel is plentiful if it can be utilized in a controlled manner.
from fusing 1.00 kg of deuterium and tritium is equivalent to 2.6 million gallons of gasoline and about eight times the energy output of the bomb that destroyed Hiroshima. Yet the average backyard swimming pool has about 6 kg of deuterium in it, so that fuel is plentiful if it can be utilized in a controlled manner.
Glossary
- nuclear fusion
- process of combining lighter nuclei to make heavier nuclei
- nuclear fusion reactor
- nuclear reactor that uses the fusion chain to produce energy
- nucleosynthesis
- process of fusion by which all elements on Earth are believed to have been created
- proton-proton chain
- combined reactions that fuse hydrogen nuclei to produce He nuclei

