Condensed Matter Physics

Molecular Spectra

Samuel J. Ling; Jeff Sanny; and William Moebs

Learning Objectives

By the end of this section, you will be able to:

  • Use the concepts of vibrational and rotational energy to describe energy transitions in a diatomic molecule
  • Explain key features of a vibrational-rotational energy spectrum of a diatomic molecule
  • Estimate allowed energies of a rotating molecule
  • Determine the equilibrium separation distance between atoms in a diatomic molecule from the vibrational-rotational absorption spectrum

Molecular energy levels are more complicated than atomic energy levels because molecules can also vibrate and rotate. The energies associated with such motions lie in different ranges and can therefore be studied separately. Electronic transitions are of order 1 eV, vibrational transitions are of order {10}^{-2}\phantom{\rule{0.2em}{0ex}}\text{eV}, and rotational transitions are of order {10}^{-3}\phantom{\rule{0.2em}{0ex}}\text{eV}\text{.} For complex molecules, these energy changes are difficult to characterize, so we begin with the simple case of a diatomic molecule.

According to classical mechanics, the energy of rotation of a diatomic molecule is given by

{E}_{r}=\frac{{L}^{2}}{2I},

where I is the moment of inertia and L is the angular momentum. According to quantum mechanics, the rotational angular momentum is quantized:

L=\sqrt{l\left(l+1\right)}\hslash \phantom{\rule{0.2em}{0ex}}\left(l=0,1,2,3\text{,...}\right),

where l is the orbital angular quantum number. The allowed rotational energy level of a diatomic molecule is therefore

{E}_{r}=l\left(l+1\right)\frac{{\hslash }^{2}}{2I}=l\left(l+1\right){E}_{0r}\phantom{\rule{0.5em}{0ex}}\left(l=0,1,2,3\text{,...}\right),

where the characteristic rotational energy of a molecule is defined as

{E}_{0r}=\frac{{\hslash }^{2}}{2I}.

For a diatomic molecule, the moment of inertia with reduced mass \mu is

I=\mu {r}_{0}^{2},

where {r}_{0} is the total distance between the atoms. The energy difference between rotational levels is therefore

\text{Δ}{E}_{r}={E}_{l+1}-{E}_{l}=2\left(l+1\right)\phantom{\rule{0.2em}{0ex}}{E}_{0r}.

A detailed study of transitions between rotational energy levels brought about by the absorption or emission of radiation (a so-called electric dipole transition) requires that

\text{Δ}l=±1.

This rule, known as a selection rule, limits the possible transitions from one quantum state to another. (Figure) is the selection rule for rotational energy transitions. It applies only to diatomic molecules that have an electric dipole moment. For this reason, symmetric molecules such as {\text{H}}_{2} and {\text{N}}_{2} do not experience rotational energy transitions due to the absorption or emission of electromagnetic radiation.

The Rotational Energy of HCl Determine the lowest three rotational energy levels of a hydrogen chloride (HCl) molecule.

Strategy Hydrogen chloride (HCl) is a diatomic molecule with an equilibrium separation distance of 0.127 nm. Rotational energy levels depend only on the momentum of inertia I and the orbital angular momentum quantum number l (in this case, l=0, 1, and 2). The momentum of inertia depends, in turn, on the equilibrium separation distance (which is given) and the reduced mass, which depends on the masses of the H and Cl atoms.

Solution First, we compute the reduced mass. If Particle 1 is hydrogen and Particle 2 is chloride, we have

\mu =\frac{{m}_{1}{m}_{2}}{{m}_{1}+{m}_{2}}=\frac{\left(1.0\phantom{\rule{0.2em}{0ex}}\text{u}\right)\left(35.4\phantom{\rule{0.2em}{0ex}}\text{u}\right)}{1.0\phantom{\rule{0.2em}{0ex}}\text{u}+35.4\phantom{\rule{0.2em}{0ex}}\text{u}}=0.97\phantom{\rule{0.2em}{0ex}}\text{u}=0.97\phantom{\rule{0.2em}{0ex}}\text{u}\left(\frac{931.5\frac{\text{MeV}}{{c}^{2}}}{1\phantom{\rule{0.2em}{0ex}}\text{u}}\right)=906\frac{\text{MeV}}{{c}^{2}}.

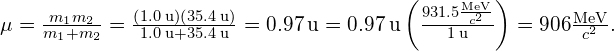
The corresponding rest mass energy is therefore

\mu {c}^{2}=9.06\phantom{\rule{0.2em}{0ex}}×\phantom{\rule{0.2em}{0ex}}{10}^{8}\phantom{\rule{0.2em}{0ex}}\text{eV}.

This allows us to calculate the characteristic energy:

{E}_{0r}=\frac{{\hslash }^{2}}{2I}=\frac{{\hslash }^{2}}{2\left(\mu {r}_{0}^{2}\right)}=\frac{{\left(\hslash c\right)}^{2}}{2\left(\mu {c}^{2}\right){r}_{0}^{2}}=\frac{{\left(197.3\phantom{\rule{0.2em}{0ex}}\text{eV}·\text{nm}\right)}^{2}}{2\left(9.06\phantom{\rule{0.2em}{0ex}}×\phantom{\rule{0.2em}{0ex}}{10}^{8}\phantom{\rule{0.2em}{0ex}}\text{eV}\right){\left(0.127\phantom{\rule{0.2em}{0ex}}\text{nm}\right)}^{2}}=1.33\phantom{\rule{0.2em}{0ex}}×\phantom{\rule{0.2em}{0ex}}{10}^{-3}\phantom{\rule{0.2em}{0ex}}\text{eV}\text{.}

(Notice how this expression is written in terms of the rest mass energy. This technique is common in modern physics calculations.) The rotational energy levels are given by

{E}_{r}=l\left(l+1\right)\frac{{\hslash }^{2}}{2I}=l\left(l+1\right){E}_{0r},

where l is the orbital quantum number. The three lowest rotational energy levels of an HCl molecule are therefore

l=0;{E}_{r}=0\phantom{\rule{0.2em}{0ex}}\text{eV}\phantom{\rule{0.2em}{0ex}}\left(\text{no rotation}\right),
l=1;{E}_{r}=2\phantom{\rule{0.2em}{0ex}}{E}_{0r}=2.66\phantom{\rule{0.2em}{0ex}}×\phantom{\rule{0.2em}{0ex}}{10}^{-3}\phantom{\rule{0.2em}{0ex}}\text{eV},
l=2;{E}_{r}=6\phantom{\rule{0.2em}{0ex}}{E}_{0r}=7.99\phantom{\rule{0.2em}{0ex}}×\phantom{\rule{0.2em}{0ex}}{10}^{-3}\phantom{\rule{0.2em}{0ex}}\text{eV}.

Significance The rotational spectrum is associated with weak transitions (1/1000 to 1/100 of an eV). By comparison, the energy of an electron in the ground state of hydrogen is -13.6\phantom{\rule{0.2em}{0ex}}\text{eV}.

Check Your Understanding What does the energy separation between absorption lines in a rotational spectrum of a diatomic molecule tell you?

the moment of inertia

The vibrational energy level, which is the energy level associated with the vibrational energy of a molecule, is more difficult to estimate than the rotational energy level. However, we can estimate these levels by assuming that the two atoms in the diatomic molecule are connected by an ideal spring of spring constant k. The potential energy of this spring system is

{U}_{\text{osc}}=\frac{1}{2}k\phantom{\rule{0.2em}{0ex}}\text{Δ}{r}^{2},

Where \text{Δ}r is a change in the “natural length” of the molecule along a line that connects the atoms. Solving Schrödinger’s equation for this potential gives

{E}_{n}=\left(n+\frac{1}{2}\right)\hslash \omega \phantom{\rule{0.2em}{0ex}}\left(n=0,1,2,\text{…}\right),

Where \omega is the natural angular frequency of vibration and n is the vibrational quantum number. The prediction that vibrational energy levels are evenly spaced \left(\text{Δ}E=\hslash \omega \right) turns out to be good at lower energies.

A detailed study of transitions between vibrational energy levels induced by the absorption or emission of radiation (and the specifically so-called electric dipole transition) requires that

\text{Δ}n=±1.

(Figure) represents the selection rule for vibrational energy transitions. As mentioned before, this rule applies only to diatomic molecules that have an electric dipole moment. Symmetric molecules do not experience such transitions.

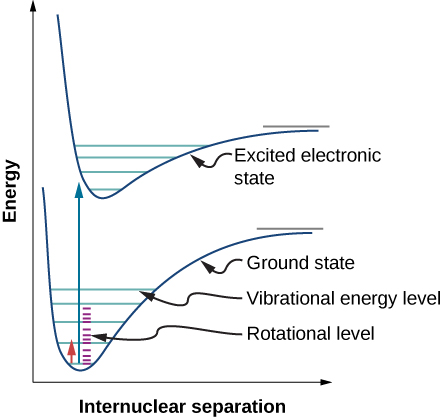
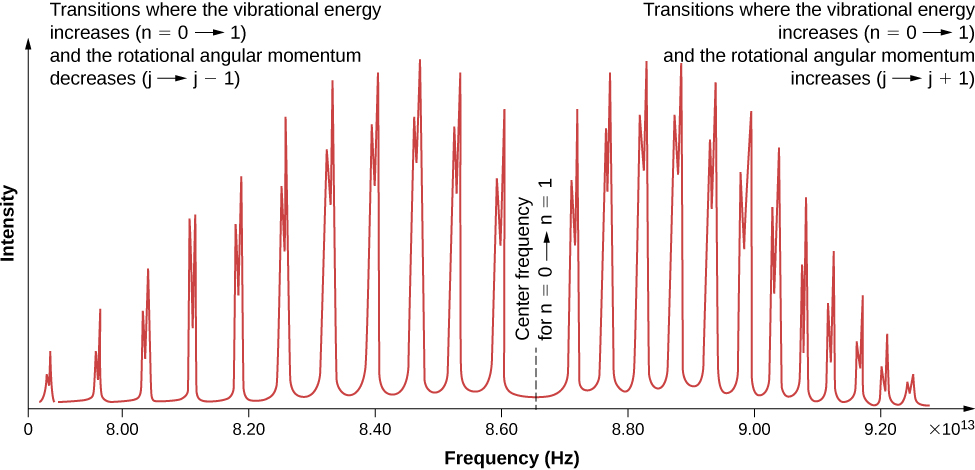
Due to the selection rules, the absorption or emission of radiation by a diatomic molecule involves a transition in vibrational and rotational states. Specifically, if the vibrational quantum number (n) changes by one unit, then the rotational quantum number (l) changes by one unit. An energy-level diagram of a possible transition is given in (Figure). The absorption spectrum for such transitions in hydrogen chloride (HCl) is shown in (Figure). The absorption peaks are due to transitions from the n=0 to n=1 vibrational states. Energy differences for the band of peaks at the left and right are, respectively, \text{Δ}{E}_{l\to l+1}=\hslash \omega +2\left(l+1\right){E}_{0r}=\hslash \omega +2{E}_{0r},\phantom{\rule{0.2em}{0ex}}\hslash \omega +4{E}_{0r},\phantom{\rule{0.2em}{0ex}}\hslash \omega +6{E}_{0r},\text{…}\phantom{\rule{0.2em}{0ex}}\left(\text{right band}\right) and \text{Δ}{E}_{l\to l-1}=\hslash \omega -2l{E}_{0r}=\hslash \omega -2{E}_{0r},\phantom{\rule{0.2em}{0ex}}\hslash \omega -4{E}_{0r},\phantom{\rule{0.2em}{0ex}}\hslash \omega -6{E}_{0r},\text{…}\phantom{\rule{0.2em}{0ex}}\left(\text{left band}\right)\text{.}

The moment of inertia can then be determined from the energy spacing between individual peaks \left(2{E}_{0r}\right) or from the gap between the left and right bands \left(4{E}_{0r}\right). The frequency at the center of this gap is the frequency of vibration.

Three types of energy levels in a diatomic molecule: electronic, vibrational, and rotational. If the vibrational quantum number (n) changes by one unit, then the rotational quantum number (l) changes by one unit.

Figure shows a graph of energy versus internuclear separation. There are two curves on the graph. The curve at the bottom is labeled ground state and the one at the top is labeled excited electronic state. Both are similar in shape, with a sharp dip to a trough, followed by a slow rise till the curve evens out. The ground state curve has five horizontal blue lines bounded by the curve, which look like rungs of a ladder. These are labeled vibrational energy level. Between two blue rungs are smaller purple rungs labeled rotational level. There are four such purple rungs each, between the first and second blue rungs, the second and third blue rungs and the third and fourth blue rungs. There is an arrow pointing up from the center of the trough. To the left of this arrow is a smaller arrow pointing up. This extends from the first purple rung of the first blue rung to the second purple rung of the second blue rung. The excited state curve has four blue rungs.

Absorption spectrum of hydrogen chloride (HCl) from the n=0\phantom{\rule{0.2em}{0ex}}\text{to}\phantom{\rule{0.2em}{0ex}}n=1 vibrational levels. The discrete peaks indicate a quantization of the angular momentum of the molecule. The bands to the left indicate a decrease in angular momentum, whereas those to the right indicate an increase in angular momentum.

Graph of intensity versus frequency in Hertz. The curve consists of several pairs of spikes. The spikes have low intensity at the beginning of the curve and also at the end of the curve at 9.2 into 10 to the power 13 hertz. The spikes are longer near the middle but dip at the center. The center frequency for n equal to 0 to n equal to 1 is approximately 8.65 into 10 to the power 13 Hertz. The left side of the graph is labeled transitions where the vibrational energy increases, n=0 to 1 and the rotational angular momentum decreases, j to j minus 1. The right side of the graph is labeled transitions where the vibrational energy increases, n=0 to 1 and the rotational angular momentum increases, j to j plus 1.

Summary

  • Molecules possess vibrational and rotational energy.
  • Energy differences between adjacent vibrational energy levels are larger than those between rotational energy levels.
  • Separation between peaks in an absorption spectrum is inversely related to the moment of inertia.
  • Transitions between vibrational and rotational energy levels follow selection rules.

Conceptual Questions

Does the absorption spectrum of the diatomic molecule HCl depend on the isotope of chlorine contained in the molecule? Explain your reasoning.

Rank the energy spacing \left(\text{Δ}E\right) of the following transitions from least to greatest: an electron energy transition in an atom (atomic energy), the rotational energy of a molecule, or the vibrational energy of a molecule?

rotational energy, vibrational energy, and atomic energy

Explain key features of a vibrational-rotation energy spectrum of the diatomic molecule.

Problems

In a physics lab, you measure the vibrational-rotational spectrum of HCl. The estimated separation between absorption peaks is \text{Δ}f\approx 5.5\phantom{\rule{0.2em}{0ex}}×\phantom{\rule{0.2em}{0ex}}{10}^{11}\phantom{\rule{0.2em}{0ex}}\text{Hz}. The central frequency of the band is {f}_{0}=9.0\phantom{\rule{0.2em}{0ex}}×\phantom{\rule{0.2em}{0ex}}{10}^{13}\phantom{\rule{0.2em}{0ex}}\text{Hz}. (a) What is the moment of inertia (I)? (b) What is the energy of vibration for the molecule?

For the preceding problem, find the equilibrium separation of the H and Cl atoms. Compare this with the actual value.

The measured value is 0.484 nm, and the actual value is close to 0.127 nm. The laboratory results are the same order of magnitude, but a factor 4 high.

The separation between oxygen atoms in an {\text{O}}_{2} molecule is about 0.121 nm. Determine the characteristic energy of rotation in eV.

The characteristic energy of the {\text{N}}_{2} molecule is 2.48\phantom{\rule{0.2em}{0ex}}×\phantom{\rule{0.2em}{0ex}}{10}^{-4}\phantom{\rule{0.2em}{0ex}}\text{eV}. Determine the separation distance between the nitrogen atoms

0.110 nm

The characteristic energy for KCl is 1.4\phantom{\rule{0.2em}{0ex}}×\phantom{\rule{0.2em}{0ex}}{10}^{-5}\phantom{\rule{0.2em}{0ex}}\text{eV.} (a) Determine \mu for the KCl molecule. (b) Find the separation distance between the K and Cl atoms.

A diatomic {\text{F}}_{2} molecule is in the l=1 state. (a) What is the energy of the molecule? (b) How much energy is radiated in a transition from a l=2 to a l=1 state?

a. E=2.2\phantom{\rule{0.2em}{0ex}}×\phantom{\rule{0.2em}{0ex}}{10}^{-4}\phantom{\rule{0.2em}{0ex}}\text{eV}; b. \text{Δ}E=4.4\phantom{\rule{0.2em}{0ex}}×\phantom{\rule{0.2em}{0ex}}{10}^{-4}\phantom{\rule{0.2em}{0ex}}\text{eV}

In a physics lab, you measure the vibrational-rotational spectrum of potassium bromide (KBr). The estimated separation between absorption peaks is \text{Δ}f\approx 5.35\phantom{\rule{0.2em}{0ex}}×\phantom{\rule{0.2em}{0ex}}{10}^{10}\phantom{\rule{0.2em}{0ex}}\text{Hz}. The central frequency of the band is {f}_{0}=8.75\phantom{\rule{0.2em}{0ex}}×\phantom{\rule{0.2em}{0ex}}{10}^{12}\phantom{\rule{0.2em}{0ex}}\text{Hz}. (a) What is the moment of inertia (I)? (b) What is the energy of vibration for the molecule?

Glossary

electric dipole transition
transition between energy levels brought by the absorption or emission of radiation
rotational energy level
energy level associated with the rotational energy of a molecule
selection rule
rule that limits the possible transitions from one quantum state to another
vibrational energy level
energy level associated with the vibrational energy of a molecule

License

Icon for the Creative Commons Attribution 4.0 International License

Molecular Spectra Copyright © by Samuel J. Ling; Jeff Sanny; and William Moebs is licensed under a Creative Commons Attribution 4.0 International License, except where otherwise noted.

Share This Book