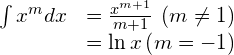Mathematical Formulas

Samuel J. Ling; Jeff Sanny; and William Moebs

Quadratic formula

If a{x}^{2}+bx+c=0, then x=\frac{\text{−}b±\sqrt{{b}^{2}-4ac}}{2a}

Geometry
Triangle of base b and height h Area =\frac{1}{2}bh
Circle of radius r Circumference =2\pi r Area =\pi {r}^{2}
Sphere of radius r Surface area =4\pi {r}^{2} Volume =\frac{4}{3}\pi {r}^{3}
Cylinder of radius r and height h Area of curved surface =2\pi rh Volume =\pi {r}^{2}h

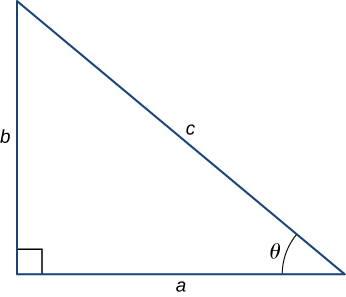
Trigonometry

Trigonometric Identities

  1. \text{sin}\phantom{\rule{0.2em}{0ex}}\theta =1\text{/}\text{csc}\phantom{\rule{0.2em}{0ex}}\theta
  2. \text{cos}\phantom{\rule{0.2em}{0ex}}\theta =1\text{/}\text{sec}\phantom{\rule{0.2em}{0ex}}\theta
  3. \text{tan}\phantom{\rule{0.2em}{0ex}}\theta =1\text{/}\text{cot}\phantom{\rule{0.2em}{0ex}}\theta
  4. \text{sin}\left({90}^{0}-\theta \right)=\text{cos}\phantom{\rule{0.2em}{0ex}}\theta
  5. \text{cos}\left({90}^{0}-\theta \right)=\text{sin}\phantom{\rule{0.2em}{0ex}}\theta
  6. \text{tan}\left({90}^{0}-\theta \right)=\text{cot}\phantom{\rule{0.2em}{0ex}}\theta
  7. {\text{sin}}^{2}\phantom{\rule{0.2em}{0ex}}\theta +{\text{cos}}^{2}\phantom{\rule{0.2em}{0ex}}\theta =1
  8. {\text{sec}}^{2}\phantom{\rule{0.2em}{0ex}}\theta -{\text{tan}}^{2}\phantom{\rule{0.2em}{0ex}}\theta =1
  9. \text{tan}\phantom{\rule{0.2em}{0ex}}\theta =\text{sin}\phantom{\rule{0.2em}{0ex}}\theta \text{/}\text{cos}\phantom{\rule{0.2em}{0ex}}\theta
  10. \text{sin}\left(\alpha ±\beta \right)=\text{sin}\phantom{\rule{0.2em}{0ex}}\alpha \phantom{\rule{0.2em}{0ex}}\text{cos}\phantom{\rule{0.2em}{0ex}}\beta ±\text{cos}\phantom{\rule{0.2em}{0ex}}\alpha \phantom{\rule{0.2em}{0ex}}\text{sin}\phantom{\rule{0.2em}{0ex}}\beta
  11. \text{cos}\left(\alpha ±\beta \right)=\text{cos}\phantom{\rule{0.2em}{0ex}}\alpha \phantom{\rule{0.2em}{0ex}}\text{cos}\phantom{\rule{0.2em}{0ex}}\beta \mp \text{sin}\phantom{\rule{0.2em}{0ex}}\alpha \phantom{\rule{0.2em}{0ex}}\text{sin}\phantom{\rule{0.2em}{0ex}}\beta
  12. \text{tan}\left(\alpha ±\beta \right)=\frac{\text{tan}\phantom{\rule{0.2em}{0ex}}\alpha ±\text{tan}\phantom{\rule{0.2em}{0ex}}\beta }{1\mp \text{tan}\phantom{\rule{0.2em}{0ex}}\alpha \phantom{\rule{0.2em}{0ex}}\text{tan}\phantom{\rule{0.2em}{0ex}}\beta }
  13. \text{sin}\phantom{\rule{0.2em}{0ex}}2\theta =2\text{sin}\phantom{\rule{0.2em}{0ex}}\theta \phantom{\rule{0.2em}{0ex}}\text{cos}\phantom{\rule{0.2em}{0ex}}\theta
  14. \text{cos}\phantom{\rule{0.2em}{0ex}}2\theta ={\text{cos}}^{2}\phantom{\rule{0.2em}{0ex}}\theta -{\text{sin}}^{2}\phantom{\rule{0.2em}{0ex}}\theta =2\phantom{\rule{0.2em}{0ex}}{\text{cos}}^{2}\phantom{\rule{0.2em}{0ex}}\theta -1=1-2\phantom{\rule{0.2em}{0ex}}{\text{sin}}^{2}\phantom{\rule{0.2em}{0ex}}\theta
  15. \text{sin}\phantom{\rule{0.2em}{0ex}}\alpha +\text{sin}\phantom{\rule{0.2em}{0ex}}\beta =2\phantom{\rule{0.2em}{0ex}}\text{sin}\frac{1}{2}\left(\alpha +\beta \right)\text{cos}\frac{1}{2}\left(\alpha -\beta \right)
  16. \text{cos}\phantom{\rule{0.2em}{0ex}}\alpha +\text{cos}\phantom{\rule{0.2em}{0ex}}\beta =2\phantom{\rule{0.2em}{0ex}}\text{cos}\frac{1}{2}\left(\alpha +\beta \right)\text{cos}\frac{1}{2}\left(\alpha -\beta \right)

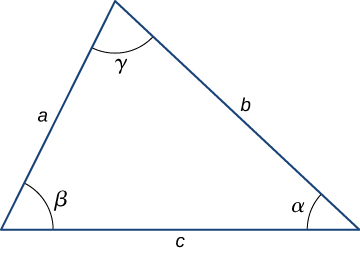
Triangles

  1. Law of sines: \frac{a}{\text{sin}\phantom{\rule{0.2em}{0ex}}\alpha }=\frac{b}{\text{sin}\phantom{\rule{0.2em}{0ex}}\beta }=\frac{c}{\text{sin}\phantom{\rule{0.2em}{0ex}}\gamma }
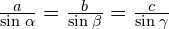
  2. Law of cosines: {c}^{2}={a}^{2}+{b}^{2}-2ab\phantom{\rule{0.2em}{0ex}}\text{cos}\phantom{\rule{0.2em}{0ex}}\gamma
     Figure shows a triangle with three dissimilar sides labeled a, b and c. All three angles of the triangle are acute angles. The angle between b and c is alpha, the angle between a and c is beta and the angle between a and b is gamma.
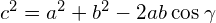
  3. Pythagorean theorem: {a}^{2}+{b}^{2}={c}^{2}
     Figure shows a right triangle. Its three sides are labeled a, b and c with c being the hypotenuse. The angle between a and c is labeled theta.

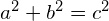
Series expansions

  1. Binomial theorem: {\left(a+b\right)}^{n}={a}^{n}+n{a}^{n-1}b+\frac{n\left(n-1\right){a}^{n-2}{b}^{2}}{2\text{!}}+\frac{n\left(n-1\right)\left(n-2\right){a}^{n-3}{b}^{3}}{3\text{!}}+\text{···}
  2. {\left(1±x\right)}^{n}=1±\frac{nx}{1\text{!}}+\frac{n\left(n-1\right){x}^{2}}{2\text{!}}±\text{···}\left({x}^{2}<1\right)
  3. {\left(1±x\right)}^{\text{−}n}=1\mp \frac{nx}{1\text{!}}+\frac{n\left(n+1\right){x}^{2}}{2\text{!}}\mp \text{···}\left({x}^{2}<1\right)
  4. \text{sin}\phantom{\rule{0.2em}{0ex}}x=x-\frac{{x}^{3}}{3\text{!}}+\frac{{x}^{5}}{5\text{!}}-\text{···}
  5. \text{cos}\phantom{\rule{0.2em}{0ex}}x=1-\frac{{x}^{2}}{2\text{!}}+\frac{{x}^{4}}{4\text{!}}-\text{···}
  6. \text{tan}\phantom{\rule{0.2em}{0ex}}x=x+\frac{{x}^{3}}{3}+\frac{2{x}^{5}}{15}+\text{···}
  7. {e}^{x}=1+x+\frac{{x}^{2}}{2\text{!}}+\text{···}
  8. \text{ln}\left(1+x\right)=x-\frac{1}{2}{x}^{2}+\frac{1}{3}{x}^{3}-\text{···}\left(|x|<1\right)

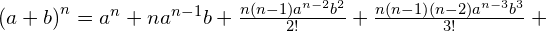
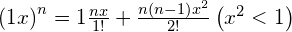
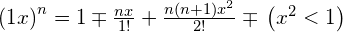
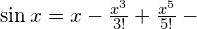
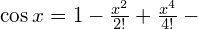
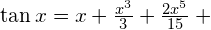
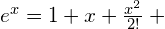
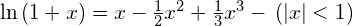
Derivatives

  1. \frac{d}{dx}\left[af\left(x\right)\right]=a\frac{d}{dx}f\left(x\right)
  2. \frac{d}{dx}\left[f\left(x\right)+g\left(x\right)\right]=\frac{d}{dx}f\left(x\right)+\frac{d}{dx}g\left(x\right)
  3. \frac{d}{dx}\left[f\left(x\right)g\left(x\right)\right]=f\left(x\right)\frac{d}{dx}g\left(x\right)+g\left(x\right)\frac{d}{dx}f\left(x\right)
  4. \frac{d}{dx}f\left(u\right)=\left[\frac{d}{du}f\left(u\right)\right]\frac{du}{dx}
  5. \frac{d}{dx}{x}^{m}=m{x}^{m-1}
  6. \frac{d}{dx}\phantom{\rule{0.2em}{0ex}}\text{sin}\phantom{\rule{0.2em}{0ex}}x=\text{cos}\phantom{\rule{0.2em}{0ex}}x
  7. \frac{d}{dx}\phantom{\rule{0.2em}{0ex}}\text{cos}\phantom{\rule{0.2em}{0ex}}x=\text{−}\text{sin}\phantom{\rule{0.2em}{0ex}}x
  8. \frac{d}{dx}\phantom{\rule{0.2em}{0ex}}\text{tan}\phantom{\rule{0.2em}{0ex}}x={\text{sec}}^{2}\phantom{\rule{0.2em}{0ex}}x
  9. \frac{d}{dx}\phantom{\rule{0.2em}{0ex}}\text{cot}\phantom{\rule{0.2em}{0ex}}x=\text{−}{\text{csc}}^{2}\phantom{\rule{0.2em}{0ex}}x
  10. \frac{d}{dx}\phantom{\rule{0.2em}{0ex}}\text{sec}\phantom{\rule{0.2em}{0ex}}x=\text{tan}\phantom{\rule{0.2em}{0ex}}x\phantom{\rule{0.2em}{0ex}}\text{sec}\phantom{\rule{0.2em}{0ex}}x
  11. \frac{d}{dx}\phantom{\rule{0.2em}{0ex}}\text{csc}\phantom{\rule{0.2em}{0ex}}x=\text{−}\text{cot}\phantom{\rule{0.2em}{0ex}}x\phantom{\rule{0.2em}{0ex}}\text{csc}\phantom{\rule{0.2em}{0ex}}x
  12. \frac{d}{dx}{e}^{x}={e}^{x}
  13. \frac{d}{dx}\phantom{\rule{0.2em}{0ex}}\text{ln}\phantom{\rule{0.2em}{0ex}}x=\frac{1}{x}
  14. \frac{d}{dx}\phantom{\rule{0.2em}{0ex}}{\text{sin}}^{-1}\phantom{\rule{0.2em}{0ex}}x=\frac{1}{\sqrt{1-{x}^{2}}}
  15. \frac{d}{dx}\phantom{\rule{0.2em}{0ex}}{\text{cos}}^{-1}x=-\frac{1}{\sqrt{1-{x}^{2}}}
  16. \frac{d}{dx}\phantom{\rule{0.2em}{0ex}}{\text{tan}}^{-1}x=-\frac{1}{1+{x}^{2}}

Integrals

  1. \int af\left(x\right)dx=a\int f\left(x\right)dx
  2. \int \left[f\left(x\right)+g\left(x\right)\right]dx=\int f\left(x\right)dx+\int g\left(x\right)dx
  3. \begin{array}{cc}\hfill \int {x}^{m}dx& =\frac{{x}^{m+1}}{m+1}\phantom{\rule{0.2em}{0ex}}\left(m\ne \text{−}1\right)\hfill \\ & =\text{ln}\phantom{\rule{0.2em}{0ex}}x\left(m=-1\right)\hfill \end{array}
  4. \int \text{sin}\phantom{\rule{0.2em}{0ex}}x\phantom{\rule{0.2em}{0ex}}dx=\text{−}\text{cos}\phantom{\rule{0.2em}{0ex}}x
  5. \int \text{cos}\phantom{\rule{0.2em}{0ex}}x\phantom{\rule{0.2em}{0ex}}dx=\text{sin}\phantom{\rule{0.2em}{0ex}}x
  6. \int \text{tan}\phantom{\rule{0.2em}{0ex}}x\phantom{\rule{0.2em}{0ex}}dx=\text{ln}|\text{sec}\phantom{\rule{0.2em}{0ex}}x|
  7. \int {\text{sin}}^{2}\phantom{\rule{0.2em}{0ex}}ax\phantom{\rule{0.2em}{0ex}}dx=\frac{x}{2}-\frac{\text{sin}\phantom{\rule{0.2em}{0ex}}2ax}{4a}
  8. \int {\text{cos}}^{2}\phantom{\rule{0.2em}{0ex}}ax\phantom{\rule{0.2em}{0ex}}dx=\frac{x}{2}+\frac{\text{sin}\phantom{\rule{0.2em}{0ex}}2ax}{4a}
  9. \int \text{sin}\phantom{\rule{0.2em}{0ex}}ax\phantom{\rule{0.2em}{0ex}}\text{cos}\phantom{\rule{0.2em}{0ex}}ax\phantom{\rule{0.2em}{0ex}}dx=-\frac{\text{cos}2ax}{4a}
  10. \int {e}^{ax}\phantom{\rule{0.2em}{0ex}}dx=\frac{1}{a}{e}^{ax}
  11. \int x{e}^{ax}dx=\frac{{e}^{ax}}{{a}^{2}}\left(ax-1\right)
  12. \int \text{ln}\phantom{\rule{0.2em}{0ex}}ax\phantom{\rule{0.2em}{0ex}}dx=x\phantom{\rule{0.2em}{0ex}}\text{ln}\phantom{\rule{0.2em}{0ex}}ax-x
  13. \int \frac{dx}{{a}^{2}+{x}^{2}}=\frac{1}{a}\phantom{\rule{0.2em}{0ex}}{\text{tan}}^{-1}\frac{x}{a}
  14. \int \frac{dx}{{a}^{2}-{x}^{2}}=\frac{1}{2a}\phantom{\rule{0.2em}{0ex}}\text{ln}|\frac{x+a}{x-a}|
  15. \int \frac{dx}{\sqrt{{a}^{2}+{x}^{2}}}={\text{sinh}}^{-1}\frac{x}{a}
  16. \int \frac{dx}{\sqrt{{a}^{2}-{x}^{2}}}={\text{sin}}^{-1}\frac{x}{a}
  17. \int \sqrt{{a}^{2}+{x}^{2}}\phantom{\rule{0.2em}{0ex}}dx=\frac{x}{2}\sqrt{{a}^{2}+{x}^{2}}+\frac{{a}^{2}}{2}\phantom{\rule{0.2em}{0ex}}{\text{sinh}}^{-1}\frac{x}{a}
  18. \int \sqrt{{a}^{2}-{x}^{2}}\phantom{\rule{0.2em}{0ex}}dx=\frac{x}{2}\sqrt{{a}^{2}-{x}^{2}}+\frac{{a}^{2}}{2}\phantom{\rule{0.2em}{0ex}}{\text{sin}}^{-1}\frac{x}{a}

License

Icon for the Creative Commons Attribution 4.0 International License

Mathematical Formulas Copyright © by Samuel J. Ling; Jeff Sanny; and William Moebs is licensed under a Creative Commons Attribution 4.0 International License, except where otherwise noted.

Share This Book