Chapter 22 Magnetism
22.8 Torque on a Current Loop: Motors and Meters
Summary
- Describe how motors and meters work in terms of torque on a current loop.
- Calculate the torque on a current-carrying loop in a magnetic field.
Motors are the most common application of magnetic force on current-carrying wires. Motors have loops of wire in a magnetic field. When current is passed through the loops, the magnetic field exerts torque on the loops, which rotates a shaft. Electrical energy is converted to mechanical work in the process. (See Figure 1.)
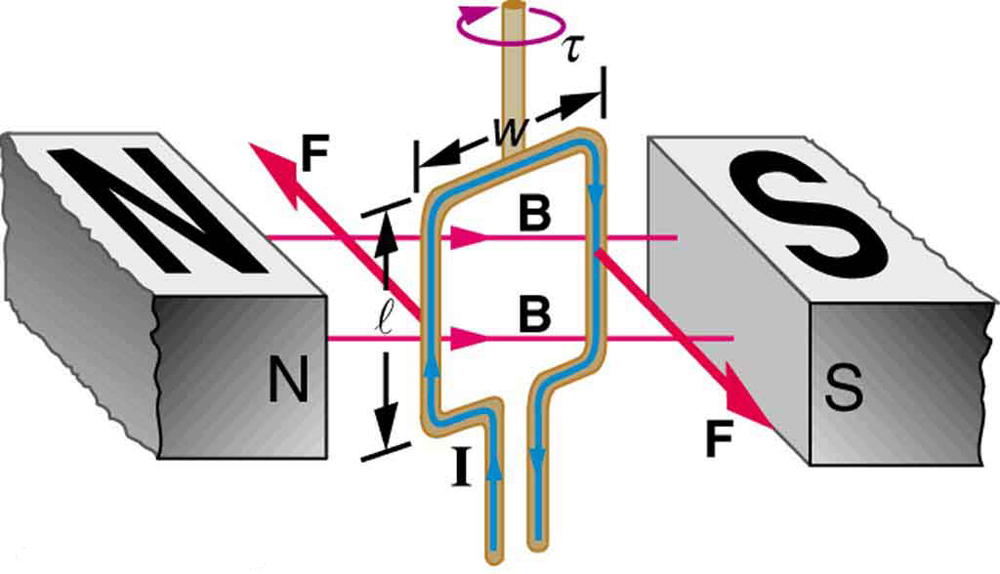
Let us examine the force on each segment of the loop in Figure 1 to find the torques produced about the axis of the vertical shaft. (This will lead to a useful equation for the torque on the loop.) We take the magnetic field to be uniform over the rectangular loop, which has width ww and height ll. First, we note that the forces on the top and bottom segments are vertical and, therefore, parallel to the shaft, producing no torque. Those vertical forces are equal in magnitude and opposite in direction, so that they also produce no net force on the loop. Figure 2 shows views of the loop from above. Torque is defined as [latex]{\tau = rF \text{sin} \;\theta}[/latex], where [latex]{F}[/latex] is the force, [latex]{r}[/latex] is the distance from the pivot that the force is applied, and [latex]{\theta}[/latex] is the angle between [latex]{r}[/latex] and [latex]{F}[/latex]. As seen in Figure 2(a), right hand rule 1 gives the forces on the sides to be equal in magnitude and opposite in direction, so that the net force is again zero. However, each force produces a clockwise torque. Since [latex]{r = w/2}[/latex], the torque on each vertical segment is [latex]{(w/2)F \;\text{sin} \;\theta}[/latex], and the two add to give a total torque.
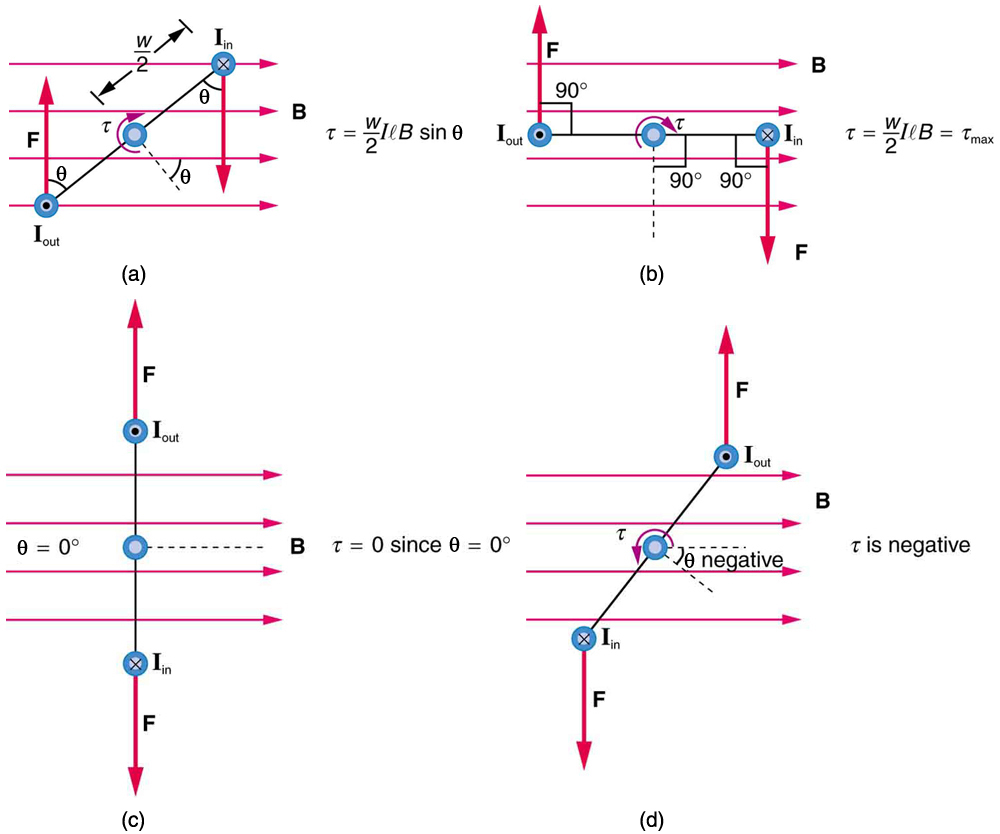
Now, each vertical segment has a length [latex]{l}[/latex] that is perpendicular to [latex]{B}[/latex], so that the force on each is [latex]{F = IlB}[/latex]. Entering [latex]{F}[/latex] into the expression for torque yields
If we have a multiple loop of [latex]{N}[/latex] turns, we get [latex]{N}[/latex] times the torque of one loop. Finally, note that the area of the loop is[/latex]latex{A = wl}[/latex]; the expression for the torque becomes
This is the torque on a current-carrying loop in a uniform magnetic field. This equation can be shown to be valid for a loop of any shape. The loop carries a current [latex]{I}[/latex], has [latex]{N}[/latex] turns, each of area [latex]{A}[/latex], and the perpendicular to the loop makes an angle [latex]{\theta}[/latex] with the field [latex]{B}[/latex]. The net force on the loop is zero.
Example 1: Calculating Torque on a Current-Carrying Loop in a Strong Magnetic Field
Find the maximum torque on a 100-turn square loop of a wire of 10.0 cm on a side that carries 15.0 A of current in a 2.00-T field.
Strategy
Torque on the loop can be found using [latex]{\tau = NIAB \;\text{sin} \;\theta}[/latex]. Maximum torque occurs when [latex]{\theta = 90^{\circ}}[/latex] and [latex]{\text{sin} \;\theta = 1}[/latex].
Solution
For [latex]{\text{sin} \;\theta = 1}[/latex], the maximum torque is
Entering known values yields
Discussion
This torque is large enough to be useful in a motor.
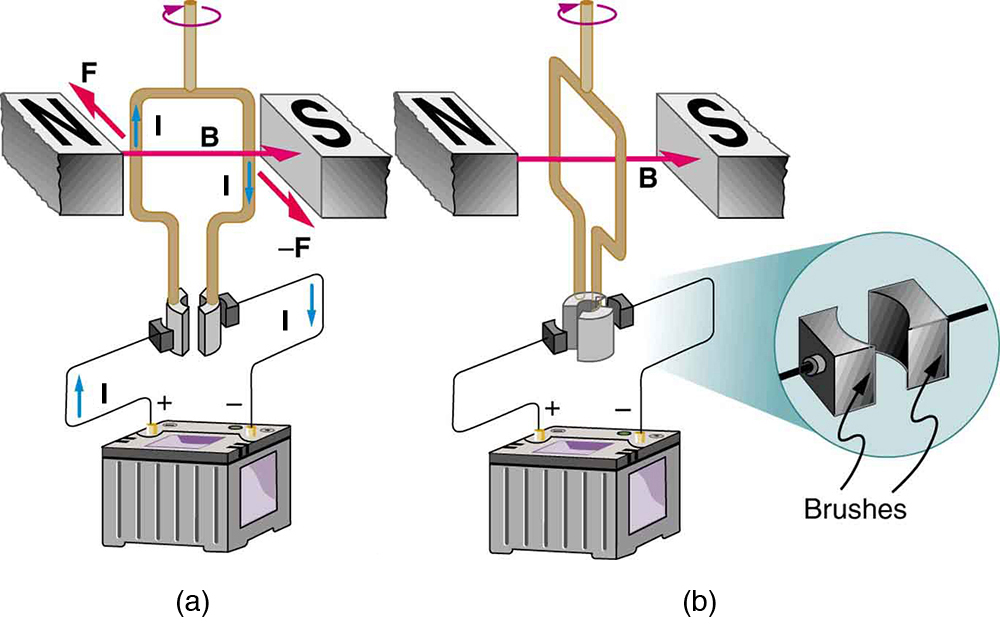
The torque found in the preceding example is the maximum. As the coil rotates, the torque decreases to zero at [latex]{\theta =0}[/latex]. The torque then reverses its direction once the coil rotates past [latex]{\theta = 0}[/latex]. (See Figure 2(d).) This means that, unless we do something, the coil will oscillate back and forth about equilibrium at [latex]{\theta = 0}[/latex]. To get the coil to continue rotating in the same direction, we can reverse the current as it passes through [latex]{\theta = 0}[/latex] with automatic switches called brushes. (See Figure 3.)
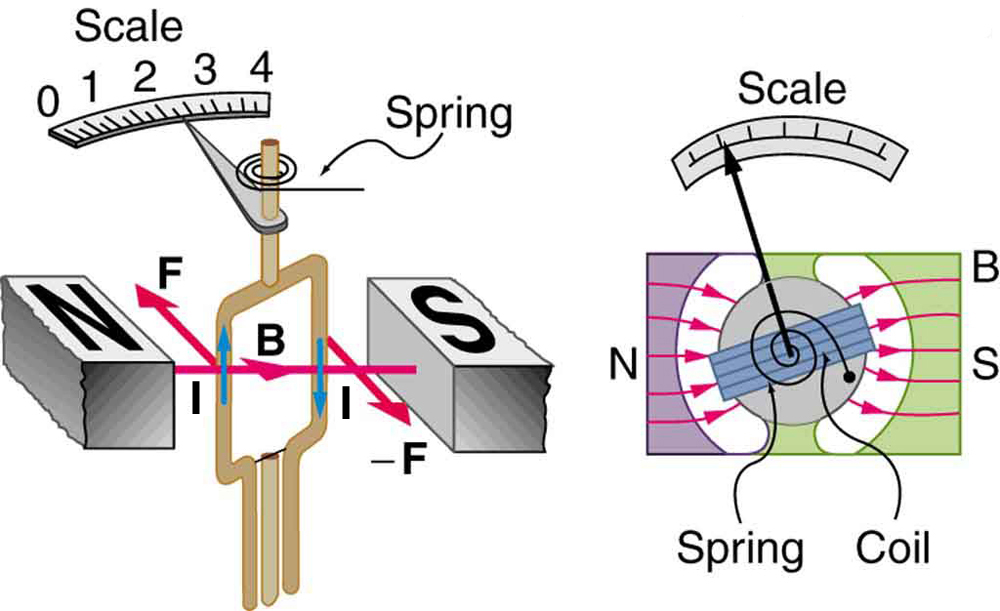
Meters, such as those in analog fuel gauges on a car, are another common application of magnetic torque on a current-carrying loop. Figure 4 shows that a meter is very similar in construction to a motor. The meter in the figure has its magnets shaped to limit the effect of [latex]{\theta}[/latex] by making [latex]{B}[/latex] perpendicular to the loop over a large angular range. Thus the torque is proportional to [latex]{I}[/latex] and not [latex]{\theta}[/latex]. A linear spring exerts a counter-torque that balances the current-produced torque. This makes the needle deflection proportional to [latex]{I}[/latex]. If an exact proportionality cannot be achieved, the gauge reading can be calibrated. To produce a galvanometer for use in analog voltmeters and ammeters that have a low resistance and respond to small currents, we use a large loop area [latex]{A}[/latex], high magnetic field [latex]{B}[/latex], and low-resistance coils.
Section Summary
- The torque [latex]{\tau}[/latex] on a current-carrying loop of any shape in a uniform magnetic field. is
[latex]{\tau = NIAB \;\text{sin} \;\theta}[/latex]
where [latex]{N}[/latex] is the number of turns, [latex]{I}[/latex] is the current, [latex]{A}[/latex] is the area of the loop, [latex]{B}[/latex] is the magnetic field strength, and [latex]{\theta}[/latex] is the angle between the perpendicular to the loop and the magnetic field.
Conceptual Questions
1: Draw a diagram and use RHR-1 to show that the forces on the top and bottom segments of the motor’s current loop in Figure 1 are vertical and produce no torque about the axis of rotation.
Problems & Exercises
1: (a) By how many percent is the torque of a motor decreased if its permanent magnets lose 5.0% of their strength? (b) How many percent would the current need to be increased to return the torque to original values?
2: (a) What is the maximum torque on a 150-turn square loop of wire 18.0 cm on a side that carries a 50.0-A current in a 1.60-T field? (b) What is the torque when [latex]{\theta}[/latex] is [latex]{10.9 ^{\circ}}[/latex]?
3: Find the current through a loop needed to create a maximum torque of [latex]{9.00 \;\text{N} \cdot \;\text{m}}[/latex]. The loop has 50 square turns that are 15.0 cm on a side and is in a uniform 0.800-T magnetic field.
4: Calculate the magnetic field strength needed on a 200-turn square loop 20.0 cm on a side to create a maximum torque of [latex]{300 \;\text{N} \cdot \;\text{m}}[/latex] if the loop is carrying 25.0 A.
5: Since the equation for torque on a current-carrying loop is [latex]{\tau = NIAB \;\text{sin} \;\theta}[/latex], the units of [latex]{\text{N} \cdot \;\text{m}}[/latex] must equal units of [latex]{\text{A} \cdot \;\text{m}^2 \;\text{T}}[/latex]. Verify this.
6: (a) At what angle [latex]{\theta}[/latex] is the torque on a current loop 90.0% of maximum? (b) 50.0% of maximum? (c) 10.0% of maximum?
7: A proton has a magnetic field due to its spin on its axis. The field is similar to that created by a circular current loop [latex]{0.650 \times 10^{-15} \;\text{m}}[/latex] in radius with a current of [latex]{1.05 \times 10^4 \;\text{A}}[/latex] (no kidding). Find the maximum torque on a proton in a 2.50-T field. (This is a significant torque on a small particle.)
8: (a) A 200-turn circular loop of radius 50.0 cm is vertical, with its axis on an east-west line. A current of 100 A circulates clockwise in the loop when viewed from the east. The Earth’s field here is due north, parallel to the ground, with a strength of [latex]{3.00 \times 10^{-5} \;\text{T}}[/latex]. What are the direction and magnitude of the torque on the loop? (b) Does this device have any practical applications as a motor?
9: Repeat Chapter 22.8 Exercises 1, but with the loop lying flat on the ground with its current circulating counterclockwise (when viewed from above) in a location where the Earth’s field is north, but at an angle [latex]{45.0 ^{\circ}}[/latex] below the horizontal and with a strength of [latex]{6.00 \times 10^{-5} \;\text{T}}[/latex].
Glossary
- motor
- loop of wire in a magnetic field; when current is passed through the loops, the magnetic field exerts torque on the loops, which rotates a shaft; electrical energy is converted to mechanical work in the process
- meter
- common application of magnetic torque on a current-carrying loop that is very similar in construction to a motor; by design, the torque is proportional to [latex]{I}[/latex] and not [latex]{\theta}[/latex], so the needle deflection is proportional to the current
Solutions
Problems & Exercises
1: (a) [latex]{\tau}[/latex] decreases by 5.00% if B decreases by 5.00%
(b) 5.26% increase
3: 10.0 A
5: [latex]{\text{A} \cdot \;\text{m}^2 \cdot \;\text{T} = \text{A} \cdot \;\text{m}^2}[/latex] [latex]{(\frac{\text{N}}{\text{A} \cdot \; \text{m}})}[/latex] [latex]{= \;\text{N} \cdot \;\text{m}}.[/latex]
7: [latex]{3.48 \times 10^{-26} \;\text{N} \cdot \;\text{m}}[/latex]
9: (a) [latex]{0.666 \;\text{N} \cdot \;\text{m} \;\text{west}}[/latex]
(b) This is not a very significant torque, so practical use would be limited. Also, the current would need to be alternated to make the loop rotate (otherwise it would oscillate).

