Particle physics as we know it today began with the ideas of Hideki Yukawa in 1935. Physicists had long been concerned with how forces are transmitted, finding the concept of fields, such as electric and magnetic fields to be very useful. A field surrounds an object and carries the force exerted by the object through space. Yukawa was interested in the strong nuclear force in particular and found an ingenious way to explain its short range. His idea is a blend of particles, forces, relativity, and quantum mechanics that is applicable to all forces. Yukawa proposed that force is transmitted by the exchange of particles (called carrier particles). The field consists of these carrier particles.

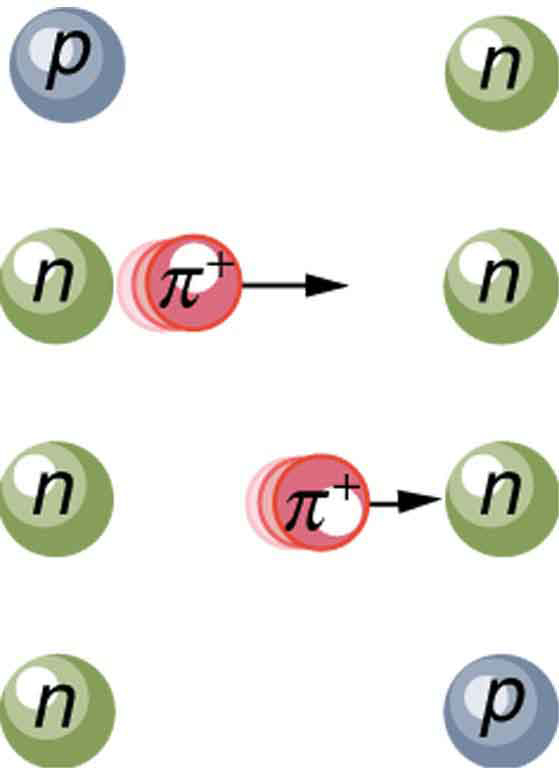
Specifically for the strong nuclear force, Yukawa proposed that a previously unknown particle, now called a pion, is exchanged between nucleons, transmitting the force between them. Figure 1 illustrates how a pion would carry a force between a proton and a neutron. The pion has mass and can only be created by violating the conservation of mass-energy. This is allowed by the Heisenberg uncertainty principle if it occurs for a sufficiently short period of time. As discussed in Chapter 29.7 Probability: The Heisenberg Uncertainty Principle the Heisenberg uncertainty principle relates the uncertainties $\mathrm{\Delta }E$ in energy and $\mathrm{\Delta }t$ in time by

where $h$ is Planck’s constant. Therefore, conservation of mass-energy can be violated by an amount $\mathrm{\Delta }E$ for a time $\mathrm{\Delta }t\approx \frac{h}{4\pi }$ in which time no process can detect the violation. This allows the temporary creation of a particle of mass $m$, where $\mathrm{\Delta }E=m{c}^2$. The larger the mass and the greater the $\mathrm{\Delta }E$, the shorter is the time it can exist. This means the range of the force is limited, because the particle can only travel a limited distance in a finite amount of time. In fact, the maximum distance is $d\approx c\mathrm{\Delta }t$, where c is the speed of light. The pion must then be captured and, thus, cannot be directly observed because that would amount to a permanent violation of mass-energy conservation. Such particles (like the pion above) are called virtual particles, because they cannot be directly observed but their effects can be directly observed. Realizing all this, Yukawa used the information on the range of the strong nuclear force to estimate the mass of the pion, the particle that carries it. The steps of his reasoning are approximately retraced in the following worked example:

Yukawa’s proposal of particle exchange as the method of force transfer is intriguing. But how can we verify his proposal if we cannot observe the virtual pion directly? If sufficient energy is in a nucleus, it would be possible to free the pion—that is, to create its mass from external energy input. This can be accomplished by collisions of energetic particles with nuclei, but energies greater than 100 MeV are required to conserve both energy and momentum. In 1947, pions were observed in cosmic-ray experiments, which were designed to supply a small flux of high-energy protons that may collide with nuclei. Soon afterward, accelerators of sufficient energy were creating pions in the laboratory under controlled conditions. Three pions were discovered, two with charge and one neutral, and given the symbols ${\pi }^{+}$, ${\pi }^{-}$, and ${\pi }^0$ respectively. The masses of ${\pi }^{+}$ and ${\pi }^{-}$ are identical at $139.6{\text{MeV/c}}^2$, whereas ${\pi }^0$ has a mass of $135.0{\text{MeV/c}}^2$. These masses are close to the predicted value of $100{\text{MeV/c}}^2$ and, since they are intermediate between electron and nucleon masses, the particles are given the name meson (now an entire class of particles, as we shall see in Chapter 33.4 Particles, Patterns, and Conservation Laws).

The pions, or $\pi$ -mesons as they are also called, have masses close to those predicted and feel the strong nuclear force. Another previously unknown particle, now called the muon, was discovered during cosmic-ray experiments in 1936 (one of its discoverers, Seth Neddermeyer, also originated the idea of implosion for plutonium bombs). Since the mass of a muon is around ${10}^6{\text{MeV/c}}^2$, at first it was thought to be the particle predicted by Yukawa. But it was soon realized that muons do not feel the strong nuclear force and could not be Yukawa’s particle. Their role was unknown, causing the respected physicist I. I. Rabi to comment, “Who ordered that?” This remains a valid question today. We have discovered hundreds of subatomic particles; the roles of some are only partially understood. But there are various patterns and relations to forces that have led to profound insights into nature’s secrets.