Chapter 9 Statics and Torque
9.3 Stability
Summary
- State the types of equilibrium.
- Describe stable and unstable equilibriums.
- Describe neutral equilibrium.
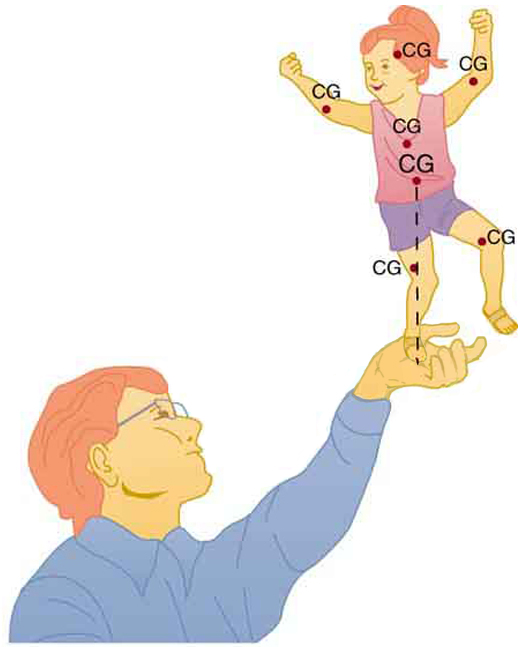
It is one thing to have a system in equilibrium; it is quite another for it to be stable. The toy doll perched on the man’s hand in Figure 1, for example, is not in stable equilibrium. There are three types of equilibrium: stable, unstable, and neutral. Figures throughout this module illustrate various examples.
Figure 1 presents a balanced system, such as the toy doll on the man’s hand, which has its center of gravity (cg) directly over the pivot, so that the torque of the total weight is zero. This is equivalent to having the torques of the individual parts balanced about the pivot point, in this case the hand. The cgs of the arms, legs, head, and torso are labeled with smaller type.
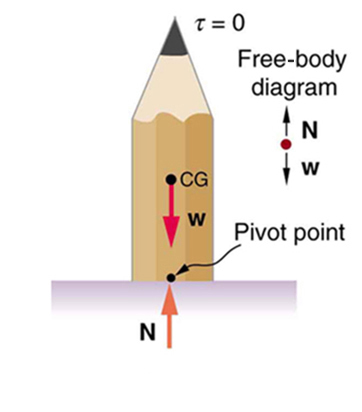
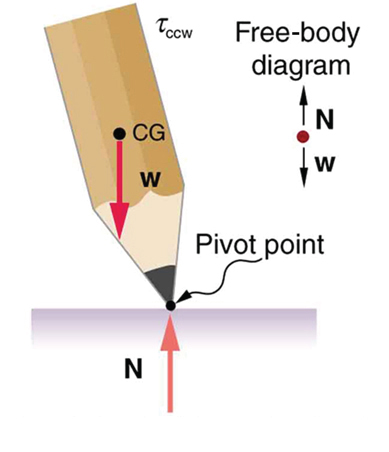
A system is said to be in stable equilibrium if, when displaced from equilibrium, it experiences a net force or torque in a direction opposite to the direction of the displacement. For example, a marble at the bottom of a bowl will experience a restoring force when displaced from its equilibrium position. This force moves it back toward the equilibrium position. Most systems are in stable equilibrium, especially for small displacements. For another example of stable equilibrium, see the pencil in Figure 2.
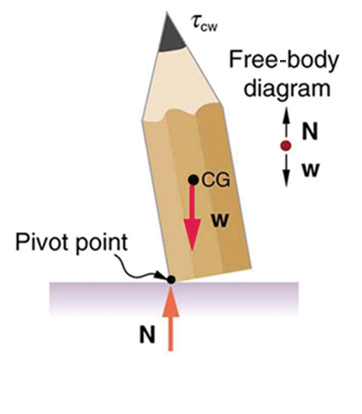
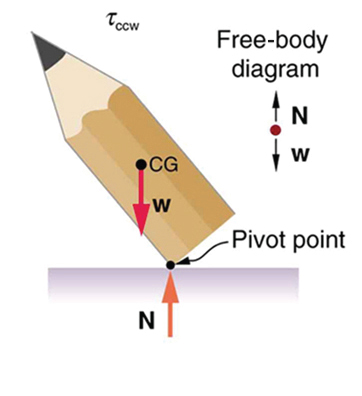
A system is in unstable equilibrium if, when displaced, it experiences a net force or torque in the same direction as the displacement from equilibrium. A system in unstable equilibrium accelerates away from its equilibrium position if displaced even slightly. An obvious example is a ball resting on top of a hill. Once displaced, it accelerates away from the crest. See the next several figures for examples of unstable equilibrium.
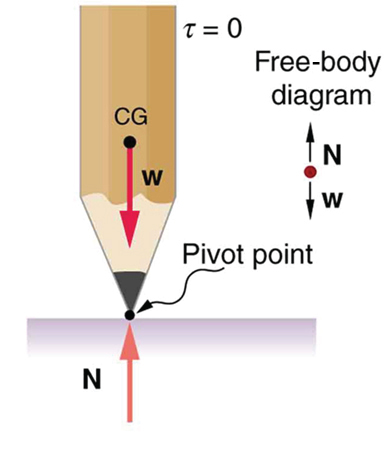
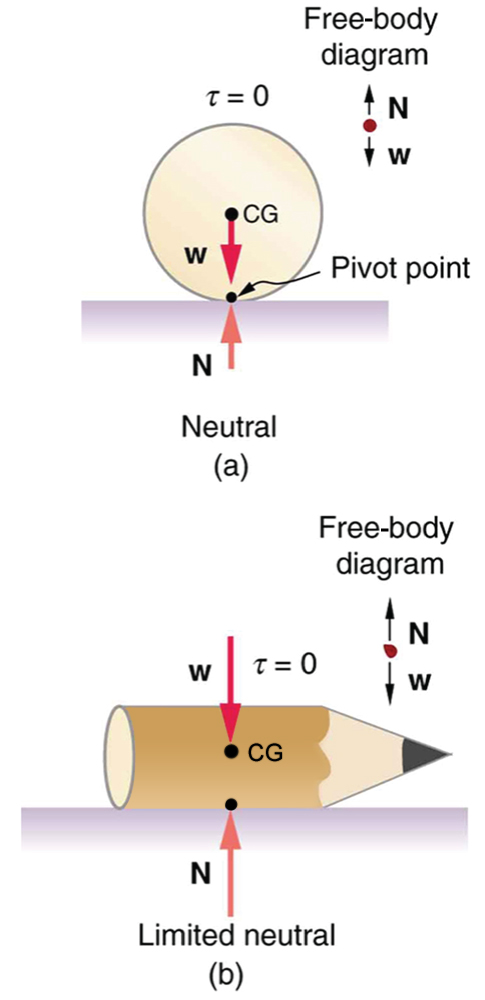
A system is in neutral equilibrium if its equilibrium is independent of displacements from its original position. A marble on a flat horizontal surface is an example. Combinations of these situations are possible. For example, a marble on a saddle is stable for displacements toward the front or back of the saddle and unstable for displacements to the side. Figure 7 shows another example of neutral equilibrium.
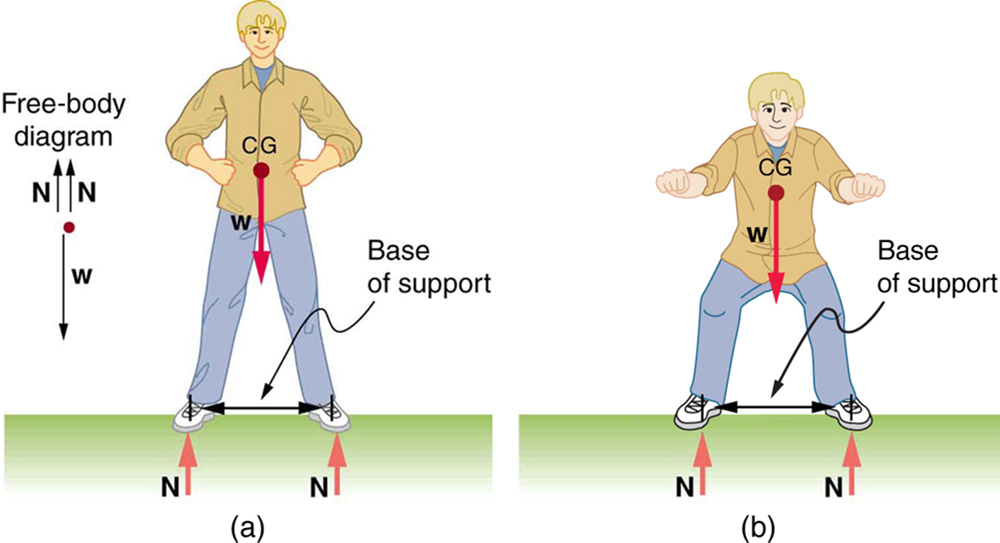
When we consider how far a system in stable equilibrium can be displaced before it becomes unstable, we find that some systems in stable equilibrium are more stable than others. The pencil in Figure 2 and the person in Figure 8(a) are in stable equilibrium, but become unstable for relatively small displacements to the side. The critical point is reached when the cg is no longer above the base of support. Additionally, since the cg of a person’s body is above the pivots in the hips, displacements must be quickly controlled. This control is a central nervous system function that is developed when we learn to hold our bodies erect as infants. For increased stability while standing, the feet should be spread apart, giving a larger base of support. Stability is also increased by lowering one’s center of gravity by bending the knees, as when a football player prepares to receive a ball or braces themselves for a tackle. A cane, a crutch, or a walker increases the stability of the user, even more as the base of support widens. Usually, the cg of a female is lower (closer to the ground) than a male. Young children have their center of gravity between their shoulders, which increases the challenge of learning to walk.
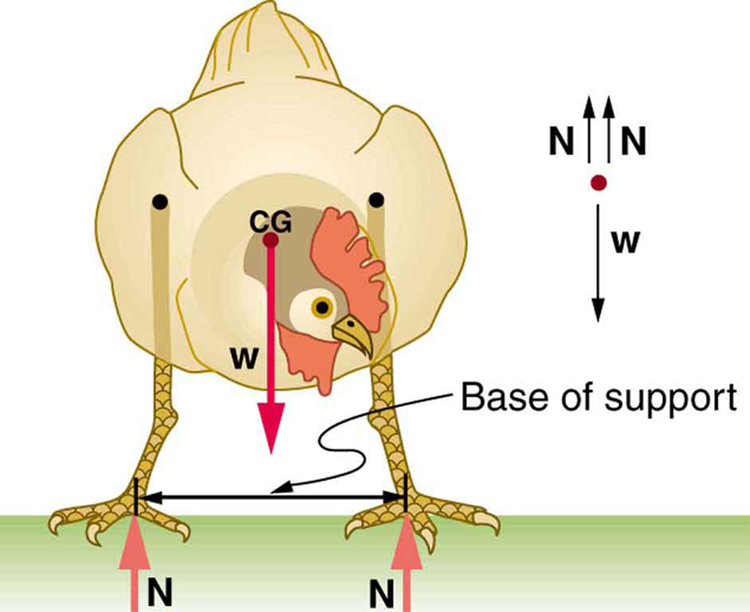
Animals such as chickens have easier systems to control. Figure 9 shows that the cg of a chicken lies below its hip joints and between its widely separated and broad feet. Even relatively large displacements of the chicken’s cg are stable and result in restoring forces and torques that return the cg to its equilibrium position with little effort on the chicken’s part. Not all birds are like chickens, of course. Some birds, such as the flamingo, have balance systems that are almost as sophisticated as that of humans.
Figure 9 shows that the cg of a chicken is below the hip joints and lies above a broad base of support formed by widely-separated and large feet. Hence, the chicken is in very stable equilibrium, since a relatively large displacement is needed to render it unstable. The body of the chicken is supported from above by the hips and acts as a pendulum between the hips. Therefore, the chicken is stable for front-to-back displacements as well as for side-to-side displacements.
Engineers and architects strive to achieve extremely stable equilibriums for buildings and other systems that must withstand wind, earthquakes, and other forces that displace them from equilibrium. Although the examples in this section emphasize gravitational forces, the basic conditions for equilibrium are the same for all types of forces. The net external force must be zero, and the net torque must also be zero.
TAKE-HOME EXPERIMENT
Stand straight with your heels, back, and head against a wall. Bend forward from your waist, keeping your heels and bottom against the wall, to touch your toes. Can you do this without toppling over? Explain why and what you need to do to be able to touch your toes without losing your balance. Is it easier for a woman to do this?
Section Summary
- A system is said to be in stable equilibrium if, when displaced from equilibrium, it experiences a net force or torque in a direction opposite the direction of the displacement.
- A system is in unstable equilibrium if, when displaced from equilibrium, it experiences a net force or torque in the same direction as the displacement from equilibrium.
- A system is in neutral equilibrium if its equilibrium is independent of displacements from its original position.
Conceptual Questions
1: A round pencil lying on its side as in Figure 4 is in neutral equilibrium relative to displacements perpendicular to its length. What is its stability relative to displacements parallel to its length?
2: Explain the need for tall towers on a suspension bridge to ensure stable equilibrium.
Problems & Exercises
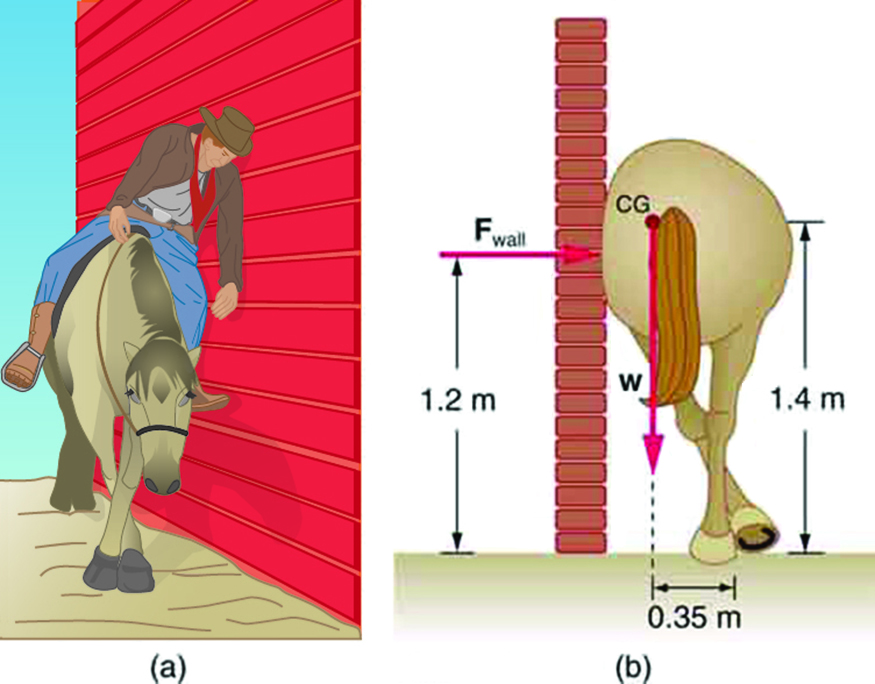
1: Suppose a horse leans against a wall as in Figure 10. Calculate the force exerted on the wall assuming that force is horizontal while using the data in the schematic representation of the situation. Note that the force exerted on the wall is equal in magnitude and opposite in direction to the force exerted on the horse, keeping it in equilibrium. The total mass of the horse and rider is 500 kg. Take the data to be accurate to three digits.
2: Two children of mass 20.0 kg and 30.0 kg sit balanced on a seesaw with the pivot point located at the center of the seesaw. If the children are separated by a distance of 3.00 m, at what distance from the pivot point is the small child sitting in order to maintain the balance?
3: (a) Calculate the magnitude and direction of the force on each foot of the horse in Figure 10 (two are on the ground), assuming the center of mass of the horse is midway between the feet. The total mass of the horse and rider is 500kg. (b) What is the minimum coefficient of friction between the hooves and ground? Note that the force exerted by the wall is horizontal.
4: A person carries a plank of wood 2.00 m long with one hand pushing down on it at one end with a force [latex]{F_1}[/latex] and the other hand holding it up at .500 m from the end of the plank with force [latex]{F_2}.[/latex] If the plank has a mass of 20.0 kg and its center of gravity is at the middle of the plank, what are the magnitudes of the forces [latex]{F_1}[/latex] and [latex]{F_2}?[/latex]
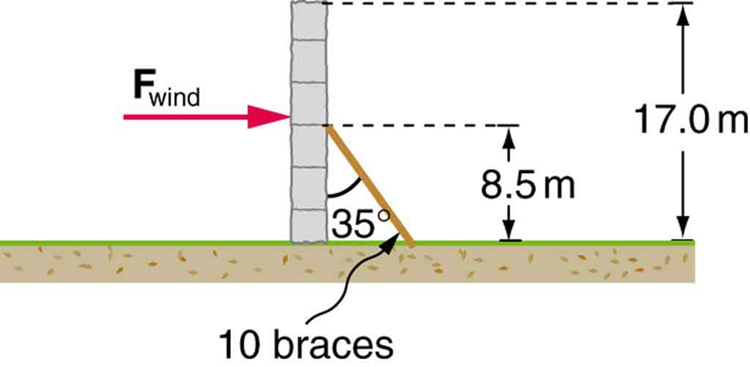
5: A 17.0-m-high and 11.0-m-long wall under construction and its bracing are shown in Figure 11. The wall is in stable equilibrium without the bracing but can pivot at its base. Calculate the force exerted by each of the 10 braces if a strong wind exerts a horizontal force of 650 N on each square meter of the wall. Assume that the net force from the wind acts at a height halfway up the wall and that all braces exert equal forces parallel to their lengths. Neglect the thickness of the wall.
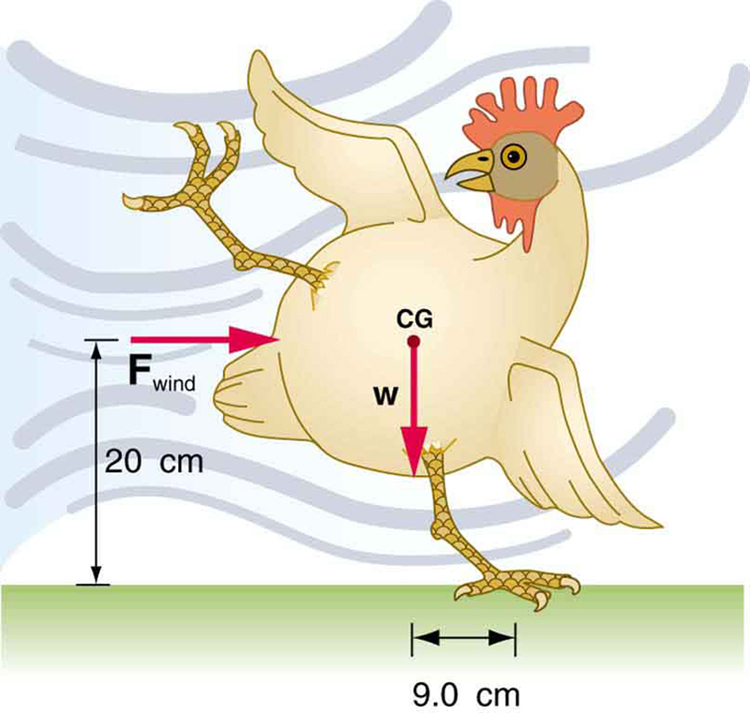
6: (a) What force must be exerted by the wind to support a 2.50-kg chicken in the position shown in Figure 12? (b) What is the ratio of this force to the chicken’s weight? (c) Does this support the contention that the chicken has a relatively stable construction?
7: Suppose the weight of the drawbridge in Figure 13 is supported entirely by its hinges and the opposite shore, so that its cables are slack. (a) What fraction of the weight is supported by the opposite shore if the point of support is directly beneath the cable attachments? (b) What is the direction and magnitude of the force the hinges exert on the bridge under these circumstances? The mass of the bridge is 2500 kg.
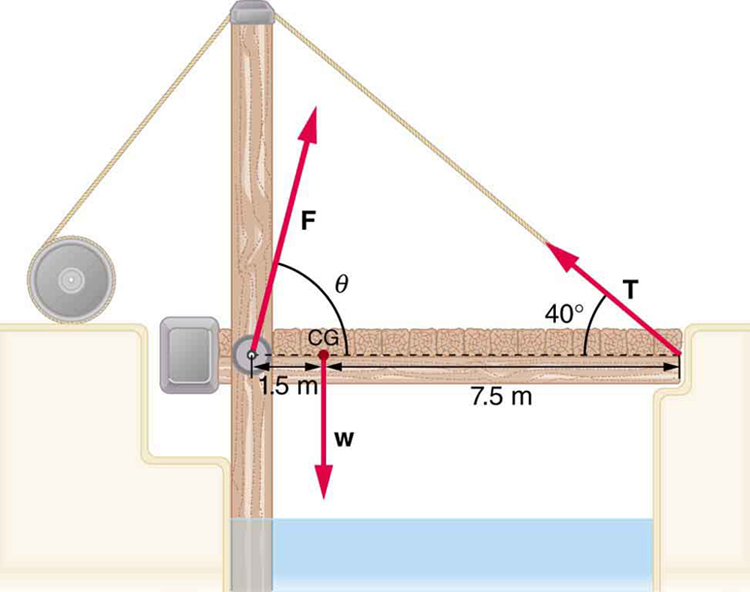
8: Suppose a 900-kg car is on the bridge in Figure 13 with its center of mass halfway between the hinges and the cable attachments. (The bridge is supported by the cables and hinges only.) (a) Find the force in the cables. (b) Find the direction and magnitude of the force exerted by the hinges on the bridge.
9: A sandwich board advertising sign is constructed as shown in Figure 14. The sign’s mass is 8.00 kg. (a) Calculate the tension in the chain assuming no friction between the legs and the sidewalk. (b) What force is exerted by each side on the hinge?
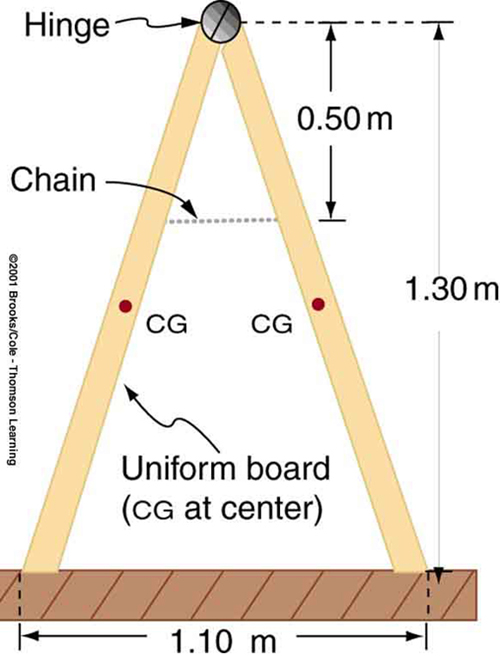
10: (a) What minimum coefficient of friction is needed between the legs and the ground to keep the sign in Figure 14 in the position shown if the chain breaks? (b) What force is exerted by each side on the hinge?
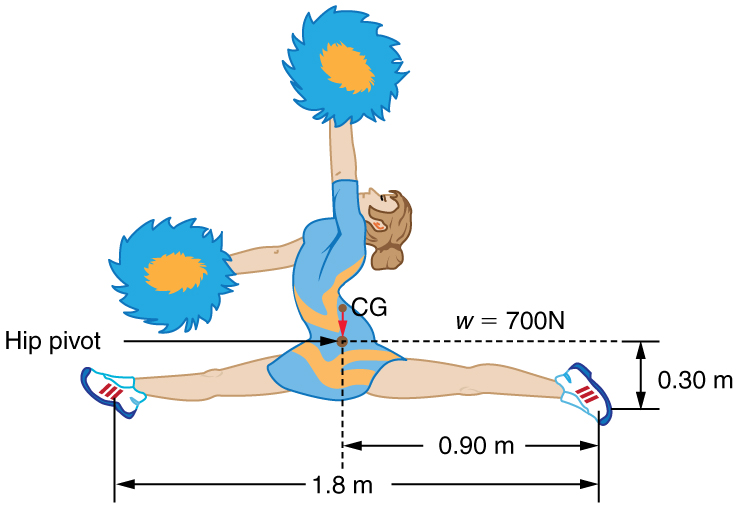
11: A gymnast is attempting to perform splits. From the information given in Figure 15, calculate the magnitude and direction of the force exerted on each foot by the floor.
Glossary
- neutral equilibrium
- a state of equilibrium that is independent of a system’s displacements from its original position
- stable equilibrium
- a system, when displaced, experiences a net force or torque in a direction opposite to the direction of the displacement
- unstable equilibrium
- a system, when displaced, experiences a net force or torque in the same direction as the displacement from equilibrium
Solutions
Problems & Exercises
1:
[latex]{F_{\text{wall}}=1.43\times10^3\text{ N}}[/latex]
3:
a) [latex]{2.55\times10^3\text{ N, }16.3^0\text{ to the left of vertical (i.e., toward the wall)}}[/latex]
b) 0.292
5:
[latex]{F_{\text{B}}=2.12\times10^4\text{ N}}[/latex]
7:
a) 0.167, or about one-sixth of the weight is supported by the opposite shore.
b) [latex]{F=2.0\times10^4\text{ N}},[/latex] straight up.
9:
a) 21.6 N
b) 21.6 N
11:
350 N directly upwards

