Simultaneity

Consider how we measure elapsed time. If we use a stopwatch, for example, how do we know when to start and stop the watch? One method is to use the arrival of light from the event, such as observing a light turning green to start a drag race. The timing will be more accurate if some sort of electronic detection is used, avoiding human reaction times and other complications.

Now suppose we use this method to measure the time interval between two flashes of light produced by flash lamps. (See Figure 2.) Two flash lamps with observer A midway between them are on a rail car that moves to the right relative to observer B. Observer B arranges for the light flashes to be emitted just as A passes B, so that both A and B are equidistant from the lamps when the light is emitted. Observer B measures the time interval between the arrival of the light flashes. According to postulate 2, the speed of light is not affected by the motion of the lamps relative to B. Therefore, light travels equal distances to him at equal speeds. Thus observer B measures the flashes to be simultaneous.

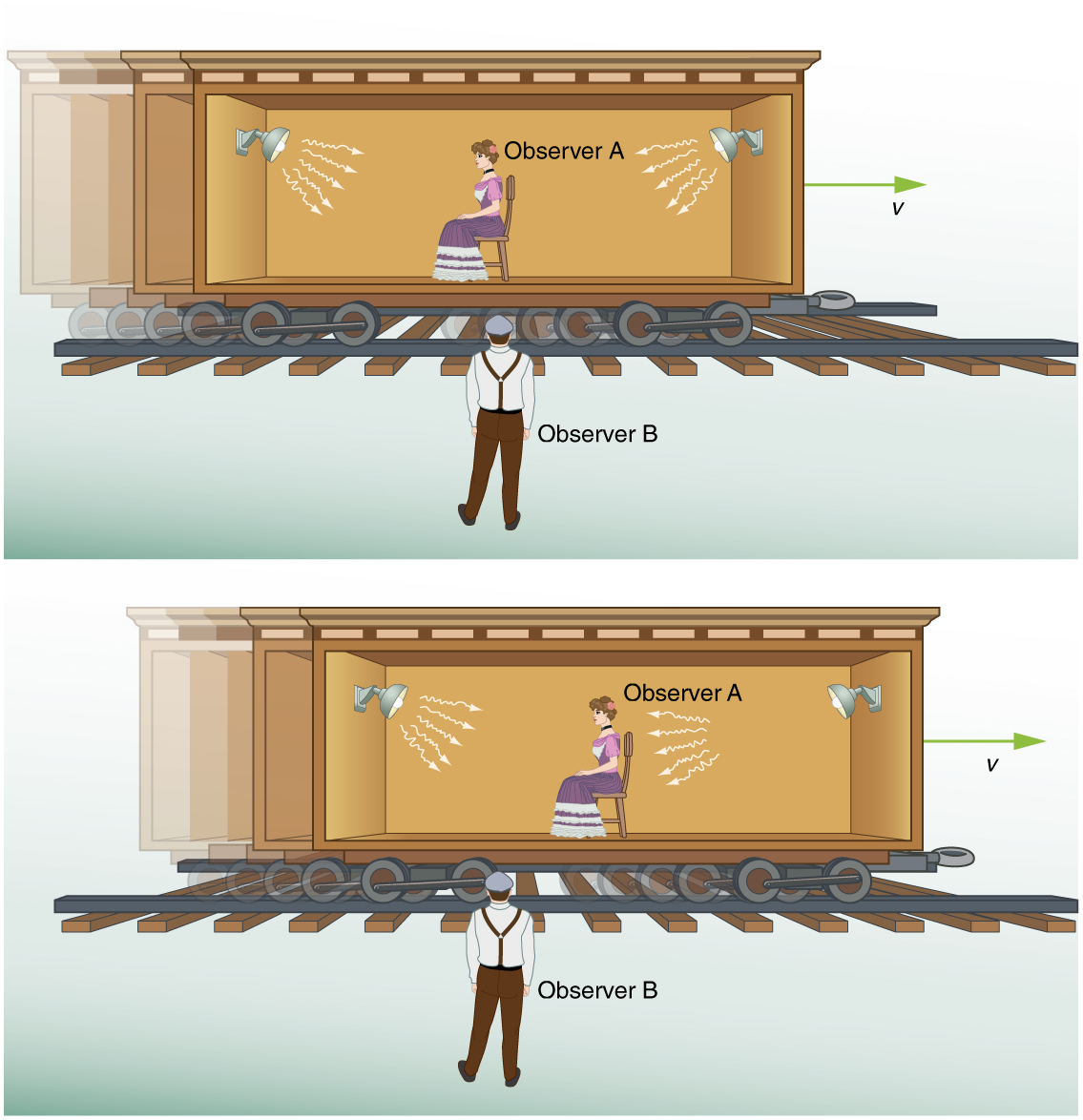
Now consider what observer B sees happen to observer A. Observer B perceives light from the right reaching observer A before light from the left, because she has moved towards that flash lamp, lessening the distance the light must travel and reducing the time it takes to get to her. Light travels at speed [latex]{c}[/latex] relative to both observers, but observer B remains equidistant between the points where the flashes were emitted, while A gets closer to the emission point on the right. From observer B’s point of view, then, there is a time interval between the arrival of the flashes to observer A. From observer B’s point of view, then, there is a time interval between the arrival of the flashes to observer A. In observer A’s frame of reference, the flashes occur at different times. Observer B measures the flashes to arrive simultaneously relative to him but not relative to A.

Now consider what observer A sees happening. She sees the light from the right arriving before light from the left. Since both lamps are the same distance from her in her reference frame, from her perspective, the right flash occurred before the left flash. Here a relative velocity between observers affects whether two events are observed to be simultaneous. Simultaneity is not absolute

This illustrates the power of clear thinking. We might have guessed incorrectly that if light is emitted simultaneously, then two observers halfway between the sources would see the flashes simultaneously. But careful analysis shows this not to be the case. Einstein was brilliant at this type of thought experiment (in German, “Gedankenexperiment”). He very carefully considered how an observation is made and disregarded what might seem obvious. The validity of thought experiments, of course, is determined by actual observation. The genius of Einstein is evidenced by the fact that experiments have repeatedly confirmed his theory of relativity.

In summary: Two events are defined to be simultaneous if an observer measures them as occurring at the same time (such as by receiving light from the events). Two events are not necessarily simultaneous to all observers.

Time Dilation

The consideration of the measurement of elapsed time and simultaneity leads to an important relativistic effect.

Suppose, for example, an astronaut measures the time it takes for light to cross her ship, bounce off a mirror, and return. (See Figure 3.) How does the elapsed time the astronaut measures compare with the elapsed time measured for the same event by a person on the Earth? Asking this question (another thought experiment) produces a profound result. We find that the elapsed time for a process depends on who is measuring it. In this case, the time measured by the astronaut is smaller than the time measured by the Earth-bound observer. The passage of time is different for the observers because the distance the light travels in the astronaut’s frame is smaller than in the Earth-bound frame. Light travels at the same speed in each frame, and so it will take longer to travel the greater distance in the Earth-bound frame.

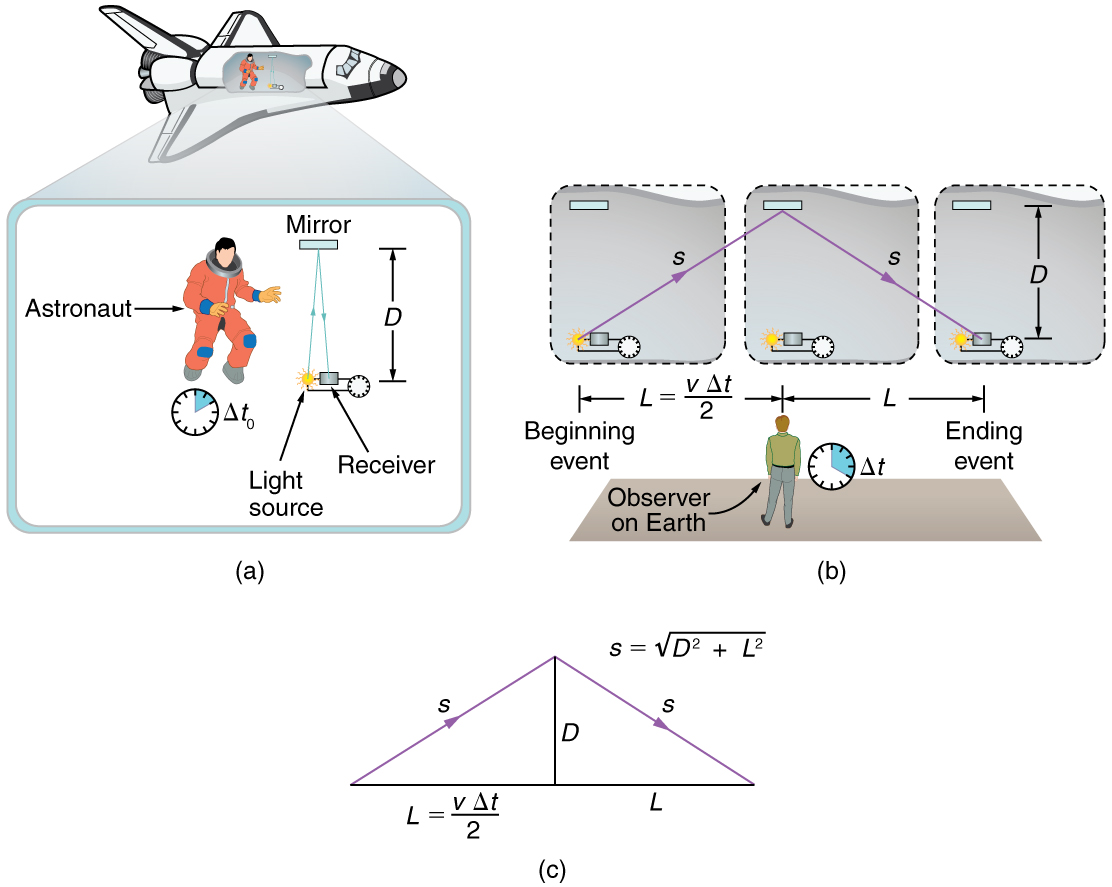
To quantitatively verify that time depends on the observer, consider the paths followed by light as seen by each observer. (See Figure 3(c).) The astronaut sees the light travel straight across and back for a total distance of [latex]{2D}[/latex], twice the width of her ship. The Earth-bound observer sees the light travel a total distance [latex]{2s}[/latex]. Since the ship is moving at speed [latex]{v}[/latex] to the right relative to the Earth, light moving to the right hits the mirror in this frame. Light travels at a speed [latex]{c}[/latex] in both frames, and because time is the distance divided by speed, the time measured by the astronaut is

This time has a separate name to distinguish it from the time measured by the Earth-bound observer.

In the case of the astronaut observe the reflecting light, the astronaut measures proper time. The time measured by the Earth-bound observer is

To find the relationship between [latex]{\Delta t_0}[/latex] and [latex]{\Delta t}[/latex], consider the triangles formed by [latex]{D}[/latex] and [latex]{s}[/latex]. (See Figure 3(c).) The third side of these similar triangles is [latex]{L}[/latex], the distance the astronaut moves as the light goes across her ship. In the frame of the Earth-bound observer,

Using the Pythagorean Theorem, the distance [latex]{s}[/latex] is found to be

Substituting [latex]{s}[/latex] into the expression for the time interval [latex]{\Delta t}[/latex] gives

We square this equation, which yields

Note that if we square the first expression we had for [latex]{\Delta t_0}[/latex], we get [latex]{(\Delta t_0)^2 = \frac{4D^2}{c2}}[/latex]. This term appears in the preceding equation, giving us a means to relate the two time intervals. Thus,

Gathering terms, we solve for [latex]{\Delta t}[/latex]:

Thus,

Taking the square root yields an important relationship between elapsed times:

where

This equation for [latex]{\Delta t}[/latex] is truly remarkable. First, as contended, elapsed time is not the same for different observers moving relative to one another, even though both are in inertial frames. Proper time [latex]{\Delta t_0}[/latex] measured by an observer, like the astronaut moving with the apparatus, is smaller than time measured by other observers. Since those other observers measure a longer time [latex]{\Delta t}[/latex], the effect is called time dilation. The Earth-bound observer sees time dilate (get longer) for a system moving relative to the Earth. Alternatively, according to the Earth-bound observer, time slows in the moving frame, since less time passes there. All clocks moving relative to an observer, including biological clocks such as aging, are observed to run slow compared with a clock stationary relative to the observer.

Note that if the relative velocity is much less than the speed of light ([latex]{v

The equation [latex]{\Delta t = \gamma \Delta t_0}[/latex] also implies that relative velocity cannot exceed the speed of light. As [latex]{v}[/latex] approaches [latex]{c}[/latex], [latex]{\Delta t}[/latex] approaches infinity. This would imply that time in the astronaut’s frame stops at the speed of light. If [latex]{v}[/latex] exceeded [latex]{c}[/latex], then we would be taking the square root of a negative number, producing an imaginary value for [latex]{\Delta t}[/latex].

There is considerable experimental evidence that the equation [latex]{\Delta t = \gamma \Delta t_0}[/latex] is correct. One example is found in cosmic ray particles that continuously rain down on the Earth from deep space. Some collisions of these particles with nuclei in the upper atmosphere result in short-lived particles called muons. The half-life (amount of time for half of a material to decay) of a muon is [latex]{1.52 \;\mu \text{s}}[/latex] when it is at rest relative to the observer who measures the half-life. This is the proper time [latex]{\Delta t_0}[/latex]. Muons produced by cosmic ray particles have a range of velocities, with some moving near the speed of light. It has been found that the muon’s half-life as measured by an Earth-bound observer ([latex]{\Delta t}[/latex]) varies with velocity exactly as predicted by the equation [latex]{\Delta t = \gamma \Delta t_0}[/latex]. The faster the muon moves, the longer it lives. We on the Earth see the muon’s half-life time dilated—as viewed from our frame, the muon decays more slowly than it does when at rest relative to us.

Example 1: Calculating Δt for a Relativistic Event: How Long Does a Speedy Muon Live?

Suppose a cosmic ray colliding with a nucleus in the Earth’s upper atmosphere produces a muon that has a velocity [latex]{v = 0.950 c}[/latex]. The muon then travels at constant velocity and lives [latex]{1.52 \;\mu \text{s}}[/latex] as measured in the muon’s frame of reference. (You can imagine this as the muon’s internal clock.) How long does the muon live as measured by an Earth-bound observer? (See Figure 4.)

 

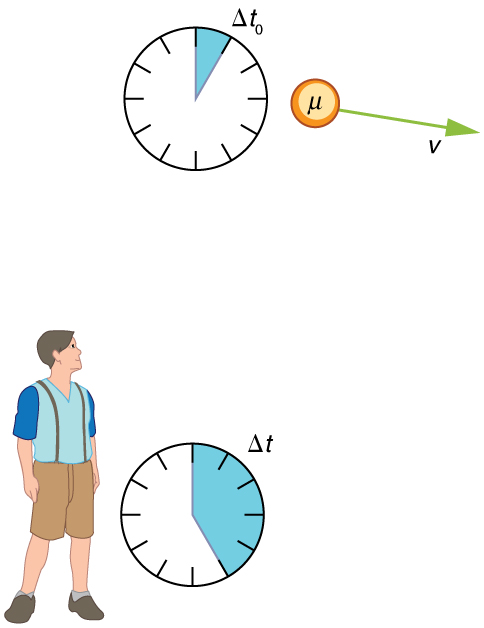
Strategy

A clock moving with the system being measured observes the proper time, so the time we are given is [latex]{\Delta t_0 = 1.52 \;\mu \text{s}}[/latex]. The Earth-bound observer measures [latex]{\Delta t}[/latex] as given by the equation [latex]{\Delta t = \gamma \Delta t_0}[/latex]. Since we know the velocity, the calculation is straightforward.

Solution

1) Identify the knowns. [latex]{v=0.950c}[/latex], [latex]{\Delta t_0 = 1.52 \;\mu \text{s}}[/latex]

2) Identify the unknown. [latex]{\Delta t}[/latex]

3) Choose the appropriate equation.

Use,

[latex]{\Delta t = \gamma \Delta t_0},[/latex]

where

[latex]{\gamma =}[/latex] [latex]{\frac{1}{\sqrt{1 - \frac{v^2}{c^2}}}}.[/latex]

4) Plug the knowns into the equation.

First find [latex]{\gamma}[/latex].

[latex]\begin{array}{r @{{}={}}l} {\gamma}\;\;= & {\frac{1}{\sqrt{1 - \frac{v^2}{c^2}}}} \\[1em] & {\frac{1}{\sqrt{1 - \frac{(0.950c)^2}{c^2}}}} \\[1em]\;= & {\frac{1}{\sqrt{1 - (0.950)^2}}} \\[1em]\;= & {3.20}. \end{array}[/latex]

Use the calculated value of [latex]{\gamma}[/latex] to determine [latex]{\Delta t}[/latex].

[latex]\begin{array}{r @{{}={}}l} {\Delta t}\;\;= & {\gamma \Delta t_0} \\[1em] & {(3.20)(1.52 \;\mu \text{s})} \\[1em]\;= & {4.87 \;\mu\text{s}} \end{array}[/latex]

Discussion

One implication of this example is that since [latex]{\gamma = 3.20}[/latex] at [latex]{95.0 \%}[/latex] of the speed of light ([latex]{v = 0.950c}[/latex]), the relativistic effects are significant. The two time intervals differ by this factor of 3.20, where classically they would be the same. Something moving at [latex]{0.950c}[/latex] is said to be highly relativistic.

Another implication of the preceding example is that everything an astronaut does when moving at [latex]{95.0 \%}[/latex] of the speed of light relative to the Earth takes 3.20 times longer when observed from the Earth. Does the astronaut sense this? Only if she looks outside her spaceship. All methods of measuring time in her frame will be affected by the same factor of 3.20. This includes her wristwatch, heart rate, cell metabolism rate, nerve impulse rate, and so on. She will have no way of telling, since all of her clocks will agree with one another because their relative velocities are zero. Motion is relative, not absolute. But what if she does look out the window?

The Twin Paradox

An intriguing consequence of time dilation is that a space traveler moving at a high velocity relative to the Earth would age less than her Earth-bound twin. Imagine the astronaut moving at such a velocity that [latex]{\gamma =30.0}[/latex], as in Figure 5. A trip that takes 2.00 years in her frame would take 60.0 years in her Earth-bound twin’s frame. Suppose the astronaut traveled 1.00 year to another star system. She briefly explored the area, and then traveled 1.00 year back. If the astronaut was 40 years old when she left, she would be 42 upon her return. Everything on the Earth, however, would have aged 60.0 years. Her twin, if still alive, would be 100 years old.

The situation would seem different to the astronaut. Because motion is relative, the spaceship would seem to be stationary and the Earth would appear to move. (This is the sensation you have when flying in a jet.) If the astronaut looks out the window of the spaceship, she will see time slow down on the Earth by a factor of [latex]{\gamma =30.0}[/latex]. To her, the Earth-bound sister will have aged only 2/30 (1/15) of a year, while she aged 2.00 years. The two sisters cannot both be correct.

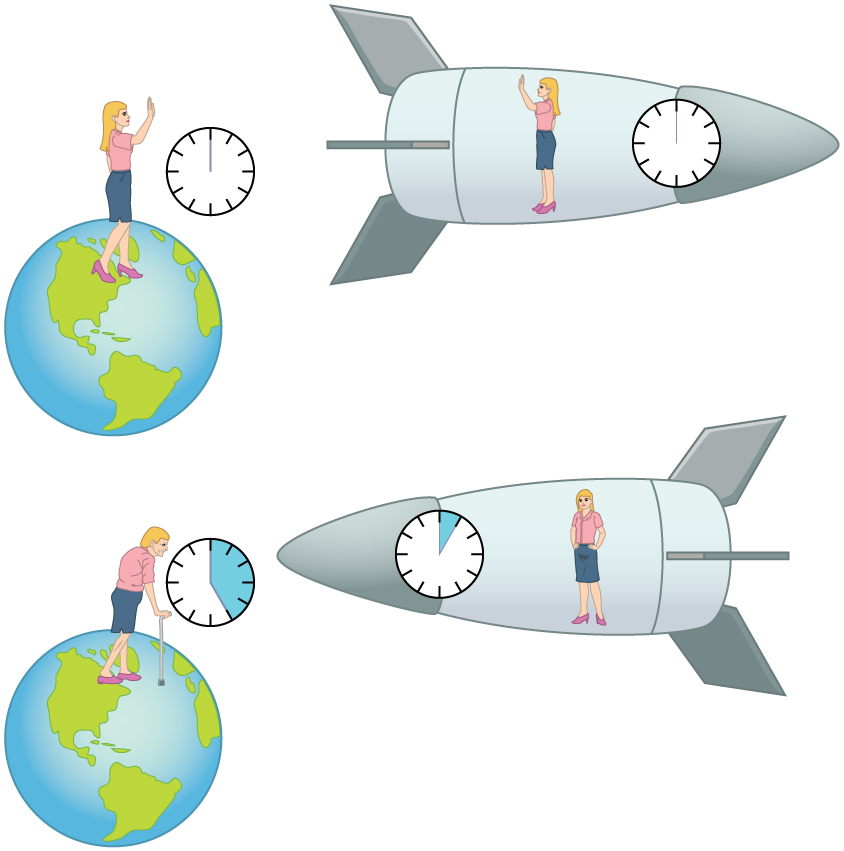
As with all paradoxes, the premise is faulty and leads to contradictory conclusions. In fact, the astronaut’s motion is significantly different from that of the Earth-bound twin. The astronaut accelerates to a high velocity and then decelerates to view the star system. To return to the Earth, she again accelerates and decelerates. The Earth-bound twin does not experience these accelerations. So the situation is not symmetric, and it is not correct to claim that the astronaut will observe the same effects as her Earth-bound twin. If you use special relativity to examine the twin paradox, you must keep in mind that the theory is expressly based on inertial frames, which by definition are not accelerated or rotating. Einstein developed general relativity to deal with accelerated frames and with gravity, a prime source of acceleration. You can also use general relativity to address the twin paradox and, according to general relativity, the astronaut will age less. Some important conceptual aspects of general relativity are discussed in Chapter 34.2 General Relativity and Quantum Gravity of this course.

In 1971, American physicists Joseph Hafele and Richard Keating verified time dilation at low relative velocities by flying extremely accurate atomic clocks around the Earth on commercial aircraft. They measured elapsed time to an accuracy of a few nanoseconds and compared it with the time measured by clocks left behind. Hafele and Keating’s results were within experimental uncertainties of the predictions of relativity. Both special and general relativity had to be taken into account, since gravity and accelerations were involved as well as relative motion.